【浙教版】2024-2025学年第一学期九年级数学期中模拟试卷(2)(含解析)
文档属性
| 名称 | 【浙教版】2024-2025学年第一学期九年级数学期中模拟试卷(2)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 721.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 15:55:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年第一学期八年级数学期中模拟试卷(2)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件中,属于必然事件的是( )
A.三角形的两边之和大于第三边 B.玩猜拳游戏时,对方出“剪刀”
C.明年的冬至会下雪 D.从装满红球的袋子里摸出黄球
2.下列各点中,抛物线y=x2﹣4x﹣4经过的点是( )
A.(0,4) B.(1,﹣7) C.(﹣1,﹣1) D.(2,8)
3.关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下 B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小 D.图象的顶点坐标为(﹣3,﹣2)
4.青田林业局考查一种树苗移植的成活率,将调查数据绘制成统计图,则可估计这种树苗移植成活的概率约是( )
A.0.95 B.0.90 C.0.85 D.0.80
5.如图,四边形ABCD内接于⊙O,AD是⊙O的直径,连接BD,若∠BCD=100°,则∠BAD的度数为( )
A.70° B.75° C.80° D.85°
6.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )
A.△ACE B.△ABD C.△ACD D.△BCE
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=8cm,则球的半径长是( )
A.4cm B.5cm C.6cm D.8cm
8.已知二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,其对称轴为直线x=﹣1,且经过点(0,1).给出下列结论:①a<0;②b=2a;③4a﹣2b+c>0;④b2﹣4ac>0.正确的是:( )
A.①② B.①②④ C.①②③ D.①②③④
9.二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
10.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是( )
A.S1<S2<S3 B.S2<S1<S3 C.S1<S3<S2 D.S3<S2<S1
二、填空题:本题共6小题,每小题3分,共18分。
11.多边形的每个内角的度数都等于140°,则这个多边形的边数为 .
12.一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同.小明通过大量随机摸球试验后,发现摸到红球的频率稳定在30%左右,则可估计红球的个数约为 .
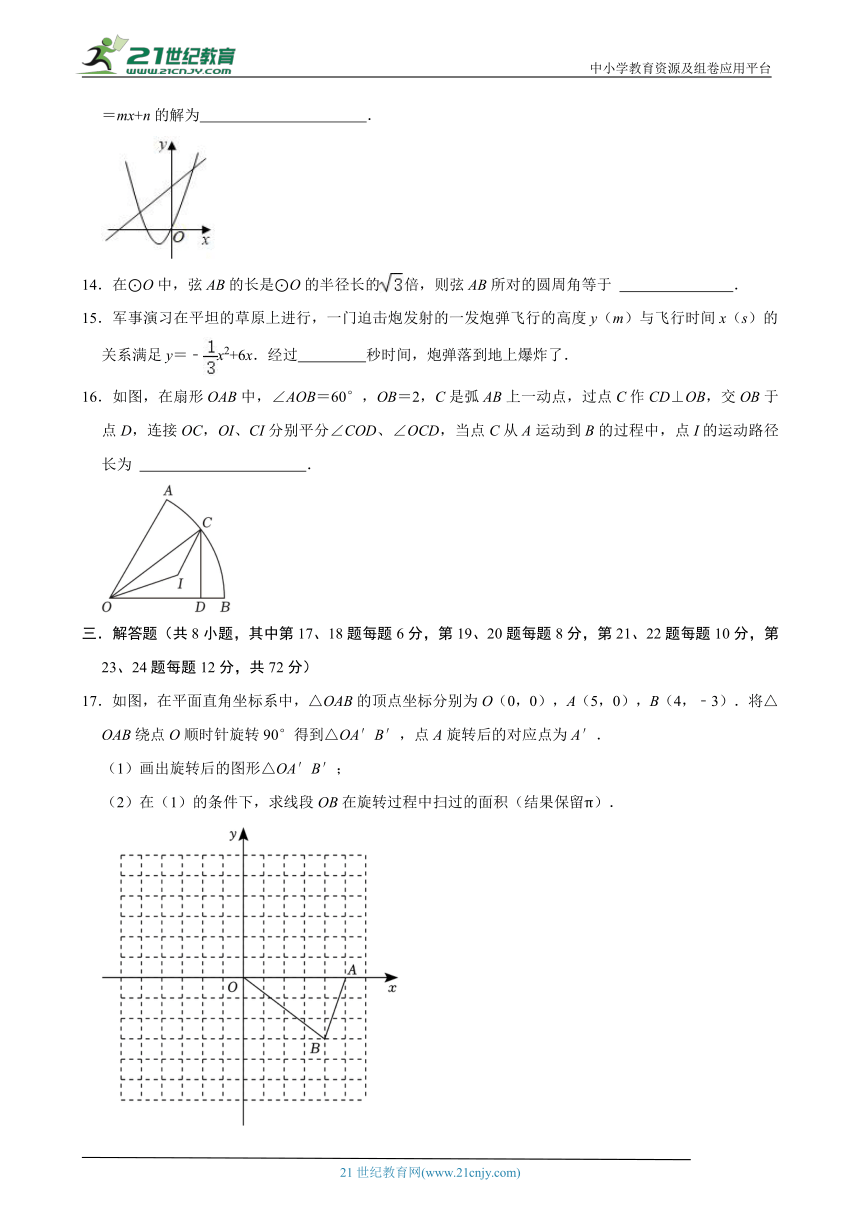
13.如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),则关于x的方程ax2+bx=mx+n的解为 .
14.在⊙O中,弦AB的长是⊙O的半径长的倍,则弦AB所对的圆周角等于 .
15.军事演坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=﹣x2+6x.经过 秒时间,炮弹落到地上爆炸了.
16.如图,在扇形OAB中,∠AOB=60°,OB=2,C是弧AB上一动点,过点C作CD⊥OB,交OB于点D,连接OC,OI、CI分别平分∠COD、∠OCD,当点C从A运动到B的过程中,点I的运动路径长为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(5,0),B(4,﹣3).将△OAB绕点O顺时针旋转90°得到△OA′B′,点A旋转后的对应点为A′.
(1)画出旋转后的图形△OA′B′;
(2)在(1)的条件下,求线段OB在旋转过程中扫过的面积(结果保留π).
18.如图,(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)若△ABC是等边三角形,AB=4.则△ABC的外接圆⊙O的半径为 .
19.小明和小乐用一副扑克牌玩游戏,两人手中各有三张扑克牌.小明的是5,7,10,小乐的是2,8,9.两人将扑克牌扣在桌面上(背面朝上),各自洗匀后分别从自己的三张牌中随机抽取一张进行比较,数字大的获胜.
(1)小乐从自己的三张牌中随机抽取一张,取出的扑克牌是2的概率是 ;
(2)请用画树状图或列表的方法说明这个游戏是否公平.
20.如图,已知二次函数y=x2+bx+c图象经过点P(1,﹣2)和C(0,﹣5).
(1)求该二次函数的解析式及图象的顶点坐标.
(2)当y≥﹣2时,请根据图象直接写出x的取值范围.
21.如图,已知BC是⊙O的一条弦,点A是⊙O的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连接BP.
(1)求证:点P为的中点;
(2)PE的长度是否会随点A的运动而变化?请说明理由.
22.随着劳动教育的开展,某学校在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为28米),用长为40米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端设计了两个宽1米的小门,便于同学们进入.
(1)若围成的菜地面积为120平方米,求此时边AB的长;
(2)可以围成的菜地面积最大是多少?
23.在平面直角坐标系xOy中,点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上.设抛物线的对称轴为直线x=t.
(1)当t=2时,
①直接写出b与a满足的等量关系;
②比较m,n的大小,并说明理由;
(2)已知点C(x0,p)在该抛物线上,若对于3<x0<4,都有m>p>n,求t的取值范围.
24.如图,AB为⊙O的直径,CD为⊙O的弦(不是直径),且CD⊥AB于点E,过点C作⊙O的直径CF,直线CB、DF交于点G.
(1)求证:△CFG为等腰三角形;
(2) ①若AB=6,求△CDF的最大面积;
②当∠ABC的度数为多少度时,以点B,O,D,F为顶点的四边形为菱形.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件中,属于必然事件的是( )
A.三角形的两边之和大于第三边 B.玩猜拳游戏时,对方出“剪刀”
C.明年的冬至会下雪 D.从装满红球的袋子里摸出黄球
【点拨】根据随机事件的定义解答即可.
【解析】解:A、三角形的两边之和大于第三边是必然事件,符合题意;
B、玩猜拳游戏时,对方出“剪刀”是随机事件,不符合题意;
C、明年的冬至会下雪是随机事件,不符合题意;
D、从装满红球的袋子里摸出黄球是不可能事件,不符合题意.
故选:A.
【点睛】本题考查的是随机事件,熟知在一定条件下,可能发生也可能不发生的事件,称为随机事件是解题的关键.
2.下列各点中,抛物线y=x2﹣4x﹣4经过的点是( )
A.(0,4) B.(1,﹣7) C.(﹣1,﹣1) D.(2,8)
【点拨】分别计算出自变量为0、1、﹣1、和2所对应的函数值,然后根据二次函数图象上点的坐标特征进行判断.
【解析】解:当x=0时,y=x2﹣4x﹣4=﹣4;当x=1时,y=x2﹣4x﹣4=﹣7;当x=﹣1时,y=x2﹣4x﹣4=1;当x=2时,y=x2﹣4x﹣4=﹣8,
所以点(1,﹣7)在抛物线y=x2﹣4x﹣4上.
故选:B.
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
3.关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下 B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小 D.图象的顶点坐标为(﹣3,﹣2)
【点拨】根据二次函数y=a(x﹣h)2+k(a≠0)的图象和性质,逐项判断即可求解.
【解析】解:∵二次函数,a=<0,
∴开口向下,顶点坐标为(3,﹣2);当x=3时,y有最大值﹣2;当x>3时,y随x的增大而减小;图象的顶点坐标为(3,﹣2);
∴D选项错误,符合题意,
故选:D.
【点睛】此题主要考查了二次函数的性质,正确把握二次函数的性质是解题关键.
4.青田林业局考查一种树苗移植的成活率,将调查数据绘制成统计图,则可估计这种树苗移植成活的概率约是( )
A.0.95 B.0.90 C.0.85 D.0.80
【点拨】由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9.
【解析】解:这种树苗成活的频率稳定在0.9,成活的概率估计值约是0.9.
故选:B.
【点睛】本题考查了利用频率估计概率.由于树苗数量巨大,故其成活的概率与频率可认为近似相等.用到的知识点为:总体数目=部分数目÷相应频率.部分的具体数目=总体数目×相应频率.
5.如图,四边形ABCD内接于⊙O,AD是⊙O的直径,连接BD,若∠BCD=100°,则∠BAD的度数为( )
A.70° B.75° C.80° D.85°
【点拨】圆内接四边形的对角互补,由此即可得到答案.
【解析】解:∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BCD=100°,
∴∠BAD=80°.
故选:C.
【点睛】本题考查圆内接四边形的性质,关键是掌握圆内接四边形的对角互补.
6.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )
A.△ACE B.△ABD C.△ACD D.△BCE
【点拨】由三角形外心的性质:三角形的外心到三角形三顶点的距离相等,即可判断.
【解析】解:由勾股定理得:PC=PE=PB==,
∴P到B、C、E的距离相等,
∴P是△BCE的外心.
故选:D.
【点睛】本题考查三角形的外接圆与外心,关键是掌握三角形外心的性质.
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=8cm,则球的半径长是( )
A.4cm B.5cm C.6cm D.8cm
【点拨】设圆心为O,过点O作ON⊥AD于点N,交CB于点M,连接OF,设OF=x cm,则ON=(8﹣x)cm,NE=NF=4,然后在Rt△NOF中利用勾股定理求得OF的长即可.
【解析】解:设圆心为O,过点O作ON⊥AD于点N,交CB于点M,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=8,
设OF=x cm,则OM=OF,
∴ON=MN﹣OM=(8﹣x)cm,NF=EN=4cm,
在Rt△ONF中,ON2+NF2=OF2
即:(8﹣x)2+42=x2
解得:x=5,
故选:B.
【点睛】本题主考查垂径定理及勾股定理的知识,正确作出辅助线构造直角三角形是解题的关键.
8.已知二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,其对称轴为直线x=﹣1,且经过点(0,1).给出下列结论:①a<0;②b=2a;③4a﹣2b+c>0;④b2﹣4ac>0.正确的是:( )
A.①② B.①②④ C.①②③ D.①②③④
【点拨】依据题意,由抛物线开口向下,则a<0,故可判断①;又对称轴是直线x=﹣=﹣1,故可判断②;又对称轴是直线x=﹣1,且当x=0时,y=1>0,则当x=﹣2时,y=4a﹣2b+c=1>0,故可判断③;又抛物线对称轴是直线x=﹣1,且抛物线与x轴的一交点为(1,0),从而另一交点为(﹣3,0),可得Δ=b2﹣4ac>0,故可判断④.
【解析】解:由题意,∵抛物线开口向下,
∴a<0,故①正确.
又对称轴是直线x=﹣=﹣1,
∴b=2a,故②正确.
∵对称轴是直线x=﹣1,
又当x=0时,y=1>0,
∴当x=﹣2时,y=4a﹣2b+c=1>0,故③正确.
又∵抛物线对称轴是直线x=﹣1,且抛物线与x轴的一交点为(1,0),
∴另一交点为(﹣3,0).
∴Δ=b2﹣4ac>0,故④正确.
综上,正确的有:①②③④.
故选:D.
【点睛】本题主要考查了二次函数的图象与性质,解题时要熟练掌握并能灵活运用是关键.
9.二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
【点拨】由二次函数解析式可得抛物线开口方向及对称轴,从而可得在﹣3≤x≤2的范围内函数取最小值时x的值,进而求解.
【解析】解:∵y=﹣x2﹣2x+c2﹣2c=﹣(x+1)2+c2﹣2c+1,
∴抛物线开口向下,对称轴为直线x=﹣1,
∵2﹣(﹣1)>﹣1﹣(﹣3),
∴在﹣3≤x≤2的范围内,x=2时,y=﹣4﹣4+c2﹣2c=c2﹣2c﹣8=(c﹣1)2﹣9为函数最小值,
∴(c﹣1)2﹣9=﹣5,
解得c=3或c=﹣1,
故选:A.
【点睛】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与不等式的关系.
10.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是( )
A.S1<S2<S3 B.S2<S1<S3 C.S1<S3<S2 D.S3<S2<S1
【点拨】设出半径,作出△COB底边BC上的高,利用扇形的面积公式和三角形的面积公式表示出三个图形面积,比较即可求解.
【解析】解:作OD⊥BC交BC与点D,
∵∠COA=60°,
∴∠COB=120°,则∠COD=60°.
∴S扇形AOC=;
S扇形BOC=.
在三角形OCD中,∠OCD=30°,
∴OD=,CD=,BC=R,
∴S△OBC=,S弓形==,
>>,
∴S2<S1<S3.
故选:B.
【点睛】此题考查扇形面积公式及弓形面积公式,解题的关键是算出三个图形的面积,首先利用扇形公式计算出第一个扇形的面积,再利用弓形等于扇形﹣三角形的关系求出弓形的面积,进行比较得出它们的面积关系.
二、填空题:本题共6小题,每小题3分,共18分。
11.多边形的每个内角的度数都等于140°,则这个多边形的边数为 9 .
【点拨】由多边形的每个内角的度数都等于140°,得这个多边形的每个外角为180°﹣140°=40°.根据多边形的外角和等于360°,那么这个多边形的边数为360°÷40°=9.
【解析】解:∵多边形的每个内角的度数都等于140°,
∴这个多边形的每个外角为180°﹣140°=40°.
又∵多边形的外角和等于360°,
∴这个多边形的边数为360°÷40°=9.
∴这个多边形的边数为9.
故答案为:9.
【点睛】本题主要考查多边形的内角与外角、任意多边形的外角和,熟练掌握多边形的内角与外角、任意多边形的外角和等于360°是解决本题的关键.
12.一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同.小明通过大量随机摸球试验后,发现摸到红球的频率稳定在30%左右,则可估计红球的个数约为 60个 .
【点拨】直接用频率乘以总数即可.
【解析】由题意可知红球的个数约为200×30%=60(个),
故答案为:60个.
【点睛】本题考查了根据频率求总数,熟记频率×总数=个数是解题的关键.
13.如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),则关于x的方程ax2+bx=mx+n的解为 x1=﹣,x2=1 .
【点拨】关于x的方程ax2+bx=mx+n的解为抛物线y=ax2+bx与直线y=mx+n交点的横坐标.
【解析】解:∵抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),
∴关于x的方程ax2+bx=mx+n的解为x1=﹣,x2=1.
故答案为:x1=﹣,x2=1.
【点睛】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.
14.在⊙O中,弦AB的长是⊙O的半径长的倍,则弦AB所对的圆周角等于 60°或120° .
【点拨】作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,根据垂径定理得AC=BC,由于AB:OA=:1,则AC:OA=:2,在Rt△OAC中,根据余弦的定义可求出∠OAC=30°,则∠AOB=120°,然后根据圆周角定理得到∠APB=∠AOB=60°,根据圆内接四边形的性质得到∠ADB=180°﹣∠APB=120°.
【解析】解:作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,如图,
∵OC⊥AB,
∴AC=BC,
∵AB:OA=:1,
∴AC:OA=:2,
在Rt△OAC中,cos∠OAC==,
∴∠OAC=30°,
而OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=∠AOB=60°,
∴∠ADB=180°﹣∠APB=120°,
即弦AB所对的圆周角等于60°或120°.
故答案为:60°或120°.
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.
15.军事演坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=﹣x2+6x.经过 18 秒时间,炮弹落到地上爆炸了.
【点拨】炮弹落到地上即y=0,代入解析式解答即可.
【解析】解:依题意,关系式化为:
y=﹣(x﹣9)2+27,
令y=0,
解得:x1=18,x2=0(不合题意,舍去),
故答案为18.
【点睛】此题主要考查了二次函数的应用,根据已知得出y=0时x的值是解题关键.
16.如图,在扇形OAB中,∠AOB=60°,OB=2,C是弧AB上一动点,过点C作CD⊥OB,交OB于点D,连接OC,OI、CI分别平分∠COD、∠OCD,当点C从A运动到B的过程中,点I的运动路径长为 π. .
【点拨】连接BI,以OB为底边作等腰直角三角形OBQ,以Q为圆心,OQ为半径作圆Q,△COI≌△BOI,从而得出∠BIO=∠CIO=135°,所以得出点I轨迹为上运动,在进一步确定I的开始和结束位置,进一步得出结果.
【解析】解:如图,
连接BI,
∵OI平分∠COD,
∴∠COI=∠BOI,
∵OC=OB,OI=OI,
∴△COI≌△BOI(SAS),
∴∠BIO=∠CIO,
∵∠CDO=90°,
∴∠COD+∠OCD=90°,
∵OI、CI分别平分∠COD、∠OCD,
∴∠COI=,
∴∠COI+∠OCD=,
∴∠BIO=∠CIO=135°,
以OB为底边作等腰直角三角形OBQ,以Q为圆心,OQ为半径作圆Q,
则点I在上运动,作AW⊥OB于W,此时I在I′处,连接OI′,
∵∠ABOI′=,∠BOQ=45°,
∴∠QI′O=∠QOI′=75°,
∴∠OQI′=30°,
∴∠BQI′=60°,
∵OQ=OB=,
∵==,
∴点I的运动路径长为,
故答案为:π.
【点睛】本题考查了全等三角形的判定和性质,确定圆的条件,弧长公式等知识,解决问题的关键是熟练掌握“定弦对定角”等模型.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(5,0),B(4,﹣3).将△OAB绕点O顺时针旋转90°得到△OA′B′,点A旋转后的对应点为A′.
(1)画出旋转后的图形△OA′B′;
(2)在(1)的条件下,求线段OB在旋转过程中扫过的面积(结果保留π).
【点拨】(1)根据旋转的性质作图即可.
(2)利用扇形面积公式计算即可.
【解析】解:(1)如图,△OA′B′即为所求.
(2)由勾股定理得,OB==5,
∴线段OB在旋转过程中扫过的面积为=.
【点睛】本题考查作图﹣旋转变换、扇形面积公式,熟练掌握旋转的性质、扇形面积公式是解答本题的关键.
18.如图,(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)若△ABC是等边三角形,AB=4.则△ABC的外接圆⊙O的半径为 .
【点拨】(1)分别作AB,BC的垂直平分线,交于点O,以O为圆心,OA为半径作⊙O,⊙O即为所求;
(2)连接OA,OB,设AB的垂直平分线OF交AB于点E,首先求出∠AOB=2∠C=120°,然后得到,根据垂直平分线的性质得到OF⊥AB,,然后利用勾股定理求解即可.
【解析】解:(1)如图,作AB,BC的垂直平分线,交于点O,以O为圆心,OA为半径作⊙O,⊙O即为所求.
(2)连接OA,OB,设AB的垂直平分线OF交AB于点E,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠AOB=2∠C=120°,
∵OA=OB,
∴,
∵OF是AB的垂直平分线,
∴OF⊥AB,,
∵∠OBA=30°,
∴,
在Rt△BOE中,OE2+BE2=OB2,
∴,
∴(负值舍去),
∴△ABC的外接圆⊙O的半径为,
故答案为:.
【点睛】本题考查了作三角形的外接圆,垂直平分线的性质,圆周角定理,勾股定理,含30°角直角三角形的性质和等边三角形的性质等知识,掌握基本作图是解题的关键.
19.小明和小乐用一副扑克牌玩游戏,两人手中各有三张扑克牌.小明的是5,7,10,小乐的是2,8,9.两人将扑克牌扣在桌面上(背面朝上),各自洗匀后分别从自己的三张牌中随机抽取一张进行比较,数字大的获胜.
(1)小乐从自己的三张牌中随机抽取一张,取出的扑克牌是2的概率是 ;
(2)请用画树状图或列表的方法说明这个游戏是否公平.
【点拨】(1)由题意知,共有3种等可能的结果,其中取出的扑克牌是2的结果有1种,利用概率公式可得答案.
(2)列表可得出所有等可能的结果数以及小明获胜的结果数、小乐获胜的结果数,再利用概率公式可得结论.
【解析】解:(1)由题意知,共有3种等可能的结果,其中取出的扑克牌是2的结果有1种,
∴取出的扑克牌是2的概率是.
故答案为:.
(2)列表如下:
2 8 9
5 (5,2) (5,8) (5,9)
7 (7,2) (7,8) (7,9)
10 (10,2) (10,8) (10,9)
共有9种等可能的结果,其中小明获胜的结果有:(5,2),(7,2),(10,2),(10,8),(10,9),共5种,
小乐获胜的结果有:(5,8),(5,9),(7,8),(7,9),共4种,
∴小明获胜的概率为,小乐获胜的概率为,
∴小明获胜的概率大,这个游戏不公平.
【点睛】本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
20.如图,已知二次函数y=x2+bx+c图象经过点P(1,﹣2)和C(0,﹣5).
(1)求该二次函数的解析式及图象的顶点坐标.
(2)当y≥﹣2时,请根据图象直接写出x的取值范围.
【点拨】(1)先把P点和C点坐标分别代入y=x2+bx+c中得到b、c的方程组,则解方程求出b、c,从而得到抛物线解析式,然后把一般式化为顶点式,从而得到抛物线的顶点坐标;
(2)先解方程x2+2x﹣5=﹣2得到x=﹣3或x=1时函数值为﹣2,然后结合函数图象写出自变量的取值范围.
【解析】解:(1)把P(1,﹣2)、C(0,﹣5)分别代入y=x2+bx+c得,
解得,
∴该二次函数的解析式为y=x2+2x﹣5;
∵y=x2+2x﹣5=(x+1)2﹣6,
∴抛物线的顶点坐标为(﹣1,﹣6);
(2)当y=﹣2时,x2+2x﹣5=﹣2,
解得x1=﹣3,x2=1,
∵抛物线的开口向上,
∴当x≤﹣3或x≥1时,y≥﹣2.
【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质.
21.如图,已知BC是⊙O的一条弦,点A是⊙O的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连接BP.
(1)求证:点P为的中点;
(2)PE的长度是否会随点A的运动而变化?请说明理由.
【点拨】(1)由于AP平分∠BAC,即∠BAP=∠CAP,则根据圆周角定理可得=,于是可判断点P为的中点;
(2)通过证明PE=PB来判断PE的长度不会随点A的运动而变化.
【解析】(1)证明:∵∠BAC的平分线AP交⊙O于点P,
即∠BAP=∠CAP,
∴=,
∴点P为的中点;
(2)解:PE的长度不会随点A的运动而变化.理由如下:
如图,
∵BE平分∠ABC,
∴∠4=∠5,
∵∠3=∠1+∠4,
而∠1=∠2,
∴∠3=∠5+∠2,
∵∠2=∠6,
∴∠3=∠5+∠6,
∴PE=PB,
∴PE的长度不会随点A的运动而变化.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等腰三角形的判断和圆周角定理.
22.随着劳动教育的开展,某学校在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为28米),用长为40米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端设计了两个宽1米的小门,便于同学们进入.
(1)若围成的菜地面积为120平方米,求此时边AB的长;
(2)可以围成的菜地面积最大是多少?
【点拨】(1)先由题意得到菜地的长AD为(40+2﹣3x)米,再列方程分情况讨论即可;
(2)设菜地的面积为S平方米,根据题意列出二次函数解析式,再根据二次函数的图象和性质作答即可.
【解析】解:(1)设菜地的宽AB为x米,
则菜地的长AD为(40+2﹣3x)米.
根据题意得x(40+2﹣3x)=120,
解得x1=4,x2=10,
当x=4时,40+2﹣3x=30>28,(不合题意,舍去);
当x=10时,40+2﹣3x=12<28,符合题意.
答:此时宽AB为10米;
(2)设菜地的面积为S平方米,则:
依题意得S=x(42﹣3x)=﹣3(x﹣7)2+147,
因为0<42﹣3x≤28,解得≤x<14;
当x=7时,S取最大值,此时S=147.
即菜地的最大面积为147平方米.
【点睛】本题考查了解一元二次方程和二次函数的图象和性质,解题时注意结果要符合题目要求.
23.在平面直角坐标系xOy中,点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上.设抛物线的对称轴为直线x=t.
(1)当t=2时,
①直接写出b与a满足的等量关系;
②比较m,n的大小,并说明理由;
(2)已知点C(x0,p)在该抛物线上,若对于3<x0<4,都有m>p>n,求t的取值范围.
【点拨】(1)①利用对称轴公式求得即可;
②利用二次函数的性质判断即可;
(2)由题意可知点A(﹣1,m)在对称轴的左侧,点B(3,n),C(x0,p)在对称轴的右侧,点A到对称轴的距离大于点C到对称轴的距离,据此即可得到,解得≤t≤3.
【解析】解:(1)①∵t=﹣=2,
∴b=﹣4a;
②∵抛物线y=ax2+bx+c中,a>0,
∴抛物线开口向上,
∵点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上,对称轴为直线x=2,
∴点A(﹣1,m)到对称轴的距离大于点B(3,n)到对称轴的距离,
∴m>n;
(2)由题意可知,点A(﹣1,m)在对称轴的左侧,点B(3,n),C(x0,p)在对称轴的右侧,
∵3<x0<4,都有m>p>n,
∴点A到对称轴的距离大于点C到对称轴的距离,
∴,解得≤t≤3,
∴t的取值范围是≤t≤3.
【点睛】本题考查了二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的性质.
24.如图,AB为⊙O的直径,CD为⊙O的弦(不是直径),且CD⊥AB于点E,过点C作⊙O的直径CF,直线CB、DF交于点G.
(1)求证:△CFG为等腰三角形;
(2) ①若AB=6,求△CDF的最大面积;
②当∠ABC的度数为多少度时,以点B,O,D,F为顶点的四边形为菱形.
【点拨】(1)先判断出AB∥DG,进而得出∠ABC=∠G,再判断出∠ABC=∠BCF,即可得出结论;
(2)先判断出DH最大时,△CDF的面积最大,计算即可得出结论;
(3)先判断出△ODF是等边三角形,进而得出∠COD=120°,再用垂径定理,求出∠AOC即可得出结论.
【解析】解:(1)∵CF是⊙O的直径,
∴∠CDF=90°,
∵CD⊥AB,
∴∠BEC=90°=∠CDG,
∴AB∥DG,
∴∠ABC=∠G,
∵OB=OC,
∴∠ABC=∠BCF,
∴∠BCF=∠G,
∴CF=GF,
∴△CFG是等腰三角形;
(2)如图1,
过点D作DH⊥CF于H,
∵AB,CF都是⊙O直径,且AB=6,
∴CF=6,
∴S△CDF=CF×DH=3DH,
要S△CDF最大,则DH最大,而DH最大=3,
即:S△CDF最大=9,
(3)如图2,当点E在OA上时,
∵AB∥DG,∴要以点B,O,D,F为顶点的四边形为菱形,只有四边形BODF是菱形,
∴OD=DF,
∵OD=OF,
∴OD=OF=DF,
∴△ODF是等边三角形,
∴∠DOF=60°
∴∠COD=120°,
∵直径AB⊥CD,
∴∠AOC=COD=60°,
∴∠ABC=AOC=30°,
当点E在OB上时,同理:∠ABC=60°
即:当∠ABC的度数为30°或60°时,以点B,O,D,F为顶点的四边形为菱形,
【点睛】此题是圆的综合题,主要考查了圆的性质,垂径定理,圆周角定理,等腰三角形的判定和性质,等边三角形的判定和性质,菱形的性质,判断出AB∥DG是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年第一学期八年级数学期中模拟试卷(2)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件中,属于必然事件的是( )
A.三角形的两边之和大于第三边 B.玩猜拳游戏时,对方出“剪刀”
C.明年的冬至会下雪 D.从装满红球的袋子里摸出黄球
2.下列各点中,抛物线y=x2﹣4x﹣4经过的点是( )
A.(0,4) B.(1,﹣7) C.(﹣1,﹣1) D.(2,8)
3.关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下 B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小 D.图象的顶点坐标为(﹣3,﹣2)
4.青田林业局考查一种树苗移植的成活率,将调查数据绘制成统计图,则可估计这种树苗移植成活的概率约是( )
A.0.95 B.0.90 C.0.85 D.0.80
5.如图,四边形ABCD内接于⊙O,AD是⊙O的直径,连接BD,若∠BCD=100°,则∠BAD的度数为( )
A.70° B.75° C.80° D.85°
6.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )
A.△ACE B.△ABD C.△ACD D.△BCE
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=8cm,则球的半径长是( )
A.4cm B.5cm C.6cm D.8cm
8.已知二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,其对称轴为直线x=﹣1,且经过点(0,1).给出下列结论:①a<0;②b=2a;③4a﹣2b+c>0;④b2﹣4ac>0.正确的是:( )
A.①② B.①②④ C.①②③ D.①②③④
9.二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
10.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是( )
A.S1<S2<S3 B.S2<S1<S3 C.S1<S3<S2 D.S3<S2<S1
二、填空题:本题共6小题,每小题3分,共18分。
11.多边形的每个内角的度数都等于140°,则这个多边形的边数为 .
12.一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同.小明通过大量随机摸球试验后,发现摸到红球的频率稳定在30%左右,则可估计红球的个数约为 .
13.如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),则关于x的方程ax2+bx=mx+n的解为 .
14.在⊙O中,弦AB的长是⊙O的半径长的倍,则弦AB所对的圆周角等于 .
15.军事演坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=﹣x2+6x.经过 秒时间,炮弹落到地上爆炸了.
16.如图,在扇形OAB中,∠AOB=60°,OB=2,C是弧AB上一动点,过点C作CD⊥OB,交OB于点D,连接OC,OI、CI分别平分∠COD、∠OCD,当点C从A运动到B的过程中,点I的运动路径长为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(5,0),B(4,﹣3).将△OAB绕点O顺时针旋转90°得到△OA′B′,点A旋转后的对应点为A′.
(1)画出旋转后的图形△OA′B′;
(2)在(1)的条件下,求线段OB在旋转过程中扫过的面积(结果保留π).
18.如图,(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)若△ABC是等边三角形,AB=4.则△ABC的外接圆⊙O的半径为 .
19.小明和小乐用一副扑克牌玩游戏,两人手中各有三张扑克牌.小明的是5,7,10,小乐的是2,8,9.两人将扑克牌扣在桌面上(背面朝上),各自洗匀后分别从自己的三张牌中随机抽取一张进行比较,数字大的获胜.
(1)小乐从自己的三张牌中随机抽取一张,取出的扑克牌是2的概率是 ;
(2)请用画树状图或列表的方法说明这个游戏是否公平.
20.如图,已知二次函数y=x2+bx+c图象经过点P(1,﹣2)和C(0,﹣5).
(1)求该二次函数的解析式及图象的顶点坐标.
(2)当y≥﹣2时,请根据图象直接写出x的取值范围.
21.如图,已知BC是⊙O的一条弦,点A是⊙O的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连接BP.
(1)求证:点P为的中点;
(2)PE的长度是否会随点A的运动而变化?请说明理由.
22.随着劳动教育的开展,某学校在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为28米),用长为40米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端设计了两个宽1米的小门,便于同学们进入.
(1)若围成的菜地面积为120平方米,求此时边AB的长;
(2)可以围成的菜地面积最大是多少?
23.在平面直角坐标系xOy中,点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上.设抛物线的对称轴为直线x=t.
(1)当t=2时,
①直接写出b与a满足的等量关系;
②比较m,n的大小,并说明理由;
(2)已知点C(x0,p)在该抛物线上,若对于3<x0<4,都有m>p>n,求t的取值范围.
24.如图,AB为⊙O的直径,CD为⊙O的弦(不是直径),且CD⊥AB于点E,过点C作⊙O的直径CF,直线CB、DF交于点G.
(1)求证:△CFG为等腰三角形;
(2) ①若AB=6,求△CDF的最大面积;
②当∠ABC的度数为多少度时,以点B,O,D,F为顶点的四边形为菱形.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件中,属于必然事件的是( )
A.三角形的两边之和大于第三边 B.玩猜拳游戏时,对方出“剪刀”
C.明年的冬至会下雪 D.从装满红球的袋子里摸出黄球
【点拨】根据随机事件的定义解答即可.
【解析】解:A、三角形的两边之和大于第三边是必然事件,符合题意;
B、玩猜拳游戏时,对方出“剪刀”是随机事件,不符合题意;
C、明年的冬至会下雪是随机事件,不符合题意;
D、从装满红球的袋子里摸出黄球是不可能事件,不符合题意.
故选:A.
【点睛】本题考查的是随机事件,熟知在一定条件下,可能发生也可能不发生的事件,称为随机事件是解题的关键.
2.下列各点中,抛物线y=x2﹣4x﹣4经过的点是( )
A.(0,4) B.(1,﹣7) C.(﹣1,﹣1) D.(2,8)
【点拨】分别计算出自变量为0、1、﹣1、和2所对应的函数值,然后根据二次函数图象上点的坐标特征进行判断.
【解析】解:当x=0时,y=x2﹣4x﹣4=﹣4;当x=1时,y=x2﹣4x﹣4=﹣7;当x=﹣1时,y=x2﹣4x﹣4=1;当x=2时,y=x2﹣4x﹣4=﹣8,
所以点(1,﹣7)在抛物线y=x2﹣4x﹣4上.
故选:B.
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
3.关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下 B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小 D.图象的顶点坐标为(﹣3,﹣2)
【点拨】根据二次函数y=a(x﹣h)2+k(a≠0)的图象和性质,逐项判断即可求解.
【解析】解:∵二次函数,a=<0,
∴开口向下,顶点坐标为(3,﹣2);当x=3时,y有最大值﹣2;当x>3时,y随x的增大而减小;图象的顶点坐标为(3,﹣2);
∴D选项错误,符合题意,
故选:D.
【点睛】此题主要考查了二次函数的性质,正确把握二次函数的性质是解题关键.
4.青田林业局考查一种树苗移植的成活率,将调查数据绘制成统计图,则可估计这种树苗移植成活的概率约是( )
A.0.95 B.0.90 C.0.85 D.0.80
【点拨】由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9.
【解析】解:这种树苗成活的频率稳定在0.9,成活的概率估计值约是0.9.
故选:B.
【点睛】本题考查了利用频率估计概率.由于树苗数量巨大,故其成活的概率与频率可认为近似相等.用到的知识点为:总体数目=部分数目÷相应频率.部分的具体数目=总体数目×相应频率.
5.如图,四边形ABCD内接于⊙O,AD是⊙O的直径,连接BD,若∠BCD=100°,则∠BAD的度数为( )
A.70° B.75° C.80° D.85°
【点拨】圆内接四边形的对角互补,由此即可得到答案.
【解析】解:∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BCD=100°,
∴∠BAD=80°.
故选:C.
【点睛】本题考查圆内接四边形的性质,关键是掌握圆内接四边形的对角互补.
6.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )
A.△ACE B.△ABD C.△ACD D.△BCE
【点拨】由三角形外心的性质:三角形的外心到三角形三顶点的距离相等,即可判断.
【解析】解:由勾股定理得:PC=PE=PB==,
∴P到B、C、E的距离相等,
∴P是△BCE的外心.
故选:D.
【点睛】本题考查三角形的外接圆与外心,关键是掌握三角形外心的性质.
7.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=8cm,则球的半径长是( )
A.4cm B.5cm C.6cm D.8cm
【点拨】设圆心为O,过点O作ON⊥AD于点N,交CB于点M,连接OF,设OF=x cm,则ON=(8﹣x)cm,NE=NF=4,然后在Rt△NOF中利用勾股定理求得OF的长即可.
【解析】解:设圆心为O,过点O作ON⊥AD于点N,交CB于点M,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=8,
设OF=x cm,则OM=OF,
∴ON=MN﹣OM=(8﹣x)cm,NF=EN=4cm,
在Rt△ONF中,ON2+NF2=OF2
即:(8﹣x)2+42=x2
解得:x=5,
故选:B.
【点睛】本题主考查垂径定理及勾股定理的知识,正确作出辅助线构造直角三角形是解题的关键.
8.已知二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,其对称轴为直线x=﹣1,且经过点(0,1).给出下列结论:①a<0;②b=2a;③4a﹣2b+c>0;④b2﹣4ac>0.正确的是:( )
A.①② B.①②④ C.①②③ D.①②③④
【点拨】依据题意,由抛物线开口向下,则a<0,故可判断①;又对称轴是直线x=﹣=﹣1,故可判断②;又对称轴是直线x=﹣1,且当x=0时,y=1>0,则当x=﹣2时,y=4a﹣2b+c=1>0,故可判断③;又抛物线对称轴是直线x=﹣1,且抛物线与x轴的一交点为(1,0),从而另一交点为(﹣3,0),可得Δ=b2﹣4ac>0,故可判断④.
【解析】解:由题意,∵抛物线开口向下,
∴a<0,故①正确.
又对称轴是直线x=﹣=﹣1,
∴b=2a,故②正确.
∵对称轴是直线x=﹣1,
又当x=0时,y=1>0,
∴当x=﹣2时,y=4a﹣2b+c=1>0,故③正确.
又∵抛物线对称轴是直线x=﹣1,且抛物线与x轴的一交点为(1,0),
∴另一交点为(﹣3,0).
∴Δ=b2﹣4ac>0,故④正确.
综上,正确的有:①②③④.
故选:D.
【点睛】本题主要考查了二次函数的图象与性质,解题时要熟练掌握并能灵活运用是关键.
9.二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
【点拨】由二次函数解析式可得抛物线开口方向及对称轴,从而可得在﹣3≤x≤2的范围内函数取最小值时x的值,进而求解.
【解析】解:∵y=﹣x2﹣2x+c2﹣2c=﹣(x+1)2+c2﹣2c+1,
∴抛物线开口向下,对称轴为直线x=﹣1,
∵2﹣(﹣1)>﹣1﹣(﹣3),
∴在﹣3≤x≤2的范围内,x=2时,y=﹣4﹣4+c2﹣2c=c2﹣2c﹣8=(c﹣1)2﹣9为函数最小值,
∴(c﹣1)2﹣9=﹣5,
解得c=3或c=﹣1,
故选:A.
【点睛】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与不等式的关系.
10.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是( )
A.S1<S2<S3 B.S2<S1<S3 C.S1<S3<S2 D.S3<S2<S1
【点拨】设出半径,作出△COB底边BC上的高,利用扇形的面积公式和三角形的面积公式表示出三个图形面积,比较即可求解.
【解析】解:作OD⊥BC交BC与点D,
∵∠COA=60°,
∴∠COB=120°,则∠COD=60°.
∴S扇形AOC=;
S扇形BOC=.
在三角形OCD中,∠OCD=30°,
∴OD=,CD=,BC=R,
∴S△OBC=,S弓形==,
>>,
∴S2<S1<S3.
故选:B.
【点睛】此题考查扇形面积公式及弓形面积公式,解题的关键是算出三个图形的面积,首先利用扇形公式计算出第一个扇形的面积,再利用弓形等于扇形﹣三角形的关系求出弓形的面积,进行比较得出它们的面积关系.
二、填空题:本题共6小题,每小题3分,共18分。
11.多边形的每个内角的度数都等于140°,则这个多边形的边数为 9 .
【点拨】由多边形的每个内角的度数都等于140°,得这个多边形的每个外角为180°﹣140°=40°.根据多边形的外角和等于360°,那么这个多边形的边数为360°÷40°=9.
【解析】解:∵多边形的每个内角的度数都等于140°,
∴这个多边形的每个外角为180°﹣140°=40°.
又∵多边形的外角和等于360°,
∴这个多边形的边数为360°÷40°=9.
∴这个多边形的边数为9.
故答案为:9.
【点睛】本题主要考查多边形的内角与外角、任意多边形的外角和,熟练掌握多边形的内角与外角、任意多边形的外角和等于360°是解决本题的关键.
12.一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同.小明通过大量随机摸球试验后,发现摸到红球的频率稳定在30%左右,则可估计红球的个数约为 60个 .
【点拨】直接用频率乘以总数即可.
【解析】由题意可知红球的个数约为200×30%=60(个),
故答案为:60个.
【点睛】本题考查了根据频率求总数,熟记频率×总数=个数是解题的关键.
13.如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),则关于x的方程ax2+bx=mx+n的解为 x1=﹣,x2=1 .
【点拨】关于x的方程ax2+bx=mx+n的解为抛物线y=ax2+bx与直线y=mx+n交点的横坐标.
【解析】解:∵抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣,1),B(1,3),
∴关于x的方程ax2+bx=mx+n的解为x1=﹣,x2=1.
故答案为:x1=﹣,x2=1.
【点睛】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.
14.在⊙O中,弦AB的长是⊙O的半径长的倍,则弦AB所对的圆周角等于 60°或120° .
【点拨】作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,根据垂径定理得AC=BC,由于AB:OA=:1,则AC:OA=:2,在Rt△OAC中,根据余弦的定义可求出∠OAC=30°,则∠AOB=120°,然后根据圆周角定理得到∠APB=∠AOB=60°,根据圆内接四边形的性质得到∠ADB=180°﹣∠APB=120°.
【解析】解:作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,如图,
∵OC⊥AB,
∴AC=BC,
∵AB:OA=:1,
∴AC:OA=:2,
在Rt△OAC中,cos∠OAC==,
∴∠OAC=30°,
而OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=∠AOB=60°,
∴∠ADB=180°﹣∠APB=120°,
即弦AB所对的圆周角等于60°或120°.
故答案为:60°或120°.
【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.
15.军事演坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=﹣x2+6x.经过 18 秒时间,炮弹落到地上爆炸了.
【点拨】炮弹落到地上即y=0,代入解析式解答即可.
【解析】解:依题意,关系式化为:
y=﹣(x﹣9)2+27,
令y=0,
解得:x1=18,x2=0(不合题意,舍去),
故答案为18.
【点睛】此题主要考查了二次函数的应用,根据已知得出y=0时x的值是解题关键.
16.如图,在扇形OAB中,∠AOB=60°,OB=2,C是弧AB上一动点,过点C作CD⊥OB,交OB于点D,连接OC,OI、CI分别平分∠COD、∠OCD,当点C从A运动到B的过程中,点I的运动路径长为 π. .
【点拨】连接BI,以OB为底边作等腰直角三角形OBQ,以Q为圆心,OQ为半径作圆Q,△COI≌△BOI,从而得出∠BIO=∠CIO=135°,所以得出点I轨迹为上运动,在进一步确定I的开始和结束位置,进一步得出结果.
【解析】解:如图,
连接BI,
∵OI平分∠COD,
∴∠COI=∠BOI,
∵OC=OB,OI=OI,
∴△COI≌△BOI(SAS),
∴∠BIO=∠CIO,
∵∠CDO=90°,
∴∠COD+∠OCD=90°,
∵OI、CI分别平分∠COD、∠OCD,
∴∠COI=,
∴∠COI+∠OCD=,
∴∠BIO=∠CIO=135°,
以OB为底边作等腰直角三角形OBQ,以Q为圆心,OQ为半径作圆Q,
则点I在上运动,作AW⊥OB于W,此时I在I′处,连接OI′,
∵∠ABOI′=,∠BOQ=45°,
∴∠QI′O=∠QOI′=75°,
∴∠OQI′=30°,
∴∠BQI′=60°,
∵OQ=OB=,
∵==,
∴点I的运动路径长为,
故答案为:π.
【点睛】本题考查了全等三角形的判定和性质,确定圆的条件,弧长公式等知识,解决问题的关键是熟练掌握“定弦对定角”等模型.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(5,0),B(4,﹣3).将△OAB绕点O顺时针旋转90°得到△OA′B′,点A旋转后的对应点为A′.
(1)画出旋转后的图形△OA′B′;
(2)在(1)的条件下,求线段OB在旋转过程中扫过的面积(结果保留π).
【点拨】(1)根据旋转的性质作图即可.
(2)利用扇形面积公式计算即可.
【解析】解:(1)如图,△OA′B′即为所求.
(2)由勾股定理得,OB==5,
∴线段OB在旋转过程中扫过的面积为=.
【点睛】本题考查作图﹣旋转变换、扇形面积公式,熟练掌握旋转的性质、扇形面积公式是解答本题的关键.
18.如图,(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)若△ABC是等边三角形,AB=4.则△ABC的外接圆⊙O的半径为 .
【点拨】(1)分别作AB,BC的垂直平分线,交于点O,以O为圆心,OA为半径作⊙O,⊙O即为所求;
(2)连接OA,OB,设AB的垂直平分线OF交AB于点E,首先求出∠AOB=2∠C=120°,然后得到,根据垂直平分线的性质得到OF⊥AB,,然后利用勾股定理求解即可.
【解析】解:(1)如图,作AB,BC的垂直平分线,交于点O,以O为圆心,OA为半径作⊙O,⊙O即为所求.
(2)连接OA,OB,设AB的垂直平分线OF交AB于点E,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠AOB=2∠C=120°,
∵OA=OB,
∴,
∵OF是AB的垂直平分线,
∴OF⊥AB,,
∵∠OBA=30°,
∴,
在Rt△BOE中,OE2+BE2=OB2,
∴,
∴(负值舍去),
∴△ABC的外接圆⊙O的半径为,
故答案为:.
【点睛】本题考查了作三角形的外接圆,垂直平分线的性质,圆周角定理,勾股定理,含30°角直角三角形的性质和等边三角形的性质等知识,掌握基本作图是解题的关键.
19.小明和小乐用一副扑克牌玩游戏,两人手中各有三张扑克牌.小明的是5,7,10,小乐的是2,8,9.两人将扑克牌扣在桌面上(背面朝上),各自洗匀后分别从自己的三张牌中随机抽取一张进行比较,数字大的获胜.
(1)小乐从自己的三张牌中随机抽取一张,取出的扑克牌是2的概率是 ;
(2)请用画树状图或列表的方法说明这个游戏是否公平.
【点拨】(1)由题意知,共有3种等可能的结果,其中取出的扑克牌是2的结果有1种,利用概率公式可得答案.
(2)列表可得出所有等可能的结果数以及小明获胜的结果数、小乐获胜的结果数,再利用概率公式可得结论.
【解析】解:(1)由题意知,共有3种等可能的结果,其中取出的扑克牌是2的结果有1种,
∴取出的扑克牌是2的概率是.
故答案为:.
(2)列表如下:
2 8 9
5 (5,2) (5,8) (5,9)
7 (7,2) (7,8) (7,9)
10 (10,2) (10,8) (10,9)
共有9种等可能的结果,其中小明获胜的结果有:(5,2),(7,2),(10,2),(10,8),(10,9),共5种,
小乐获胜的结果有:(5,8),(5,9),(7,8),(7,9),共4种,
∴小明获胜的概率为,小乐获胜的概率为,
∴小明获胜的概率大,这个游戏不公平.
【点睛】本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
20.如图,已知二次函数y=x2+bx+c图象经过点P(1,﹣2)和C(0,﹣5).
(1)求该二次函数的解析式及图象的顶点坐标.
(2)当y≥﹣2时,请根据图象直接写出x的取值范围.
【点拨】(1)先把P点和C点坐标分别代入y=x2+bx+c中得到b、c的方程组,则解方程求出b、c,从而得到抛物线解析式,然后把一般式化为顶点式,从而得到抛物线的顶点坐标;
(2)先解方程x2+2x﹣5=﹣2得到x=﹣3或x=1时函数值为﹣2,然后结合函数图象写出自变量的取值范围.
【解析】解:(1)把P(1,﹣2)、C(0,﹣5)分别代入y=x2+bx+c得,
解得,
∴该二次函数的解析式为y=x2+2x﹣5;
∵y=x2+2x﹣5=(x+1)2﹣6,
∴抛物线的顶点坐标为(﹣1,﹣6);
(2)当y=﹣2时,x2+2x﹣5=﹣2,
解得x1=﹣3,x2=1,
∵抛物线的开口向上,
∴当x≤﹣3或x≥1时,y≥﹣2.
【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质.
21.如图,已知BC是⊙O的一条弦,点A是⊙O的优弧BC上的一个动点(点A与B,C不重合),∠BAC的平分线AP交⊙O于点P.∠ABC的平分线BE交AP于点E,连接BP.
(1)求证:点P为的中点;
(2)PE的长度是否会随点A的运动而变化?请说明理由.
【点拨】(1)由于AP平分∠BAC,即∠BAP=∠CAP,则根据圆周角定理可得=,于是可判断点P为的中点;
(2)通过证明PE=PB来判断PE的长度不会随点A的运动而变化.
【解析】(1)证明:∵∠BAC的平分线AP交⊙O于点P,
即∠BAP=∠CAP,
∴=,
∴点P为的中点;
(2)解:PE的长度不会随点A的运动而变化.理由如下:
如图,
∵BE平分∠ABC,
∴∠4=∠5,
∵∠3=∠1+∠4,
而∠1=∠2,
∴∠3=∠5+∠2,
∵∠2=∠6,
∴∠3=∠5+∠6,
∴PE=PB,
∴PE的长度不会随点A的运动而变化.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等腰三角形的判断和圆周角定理.
22.随着劳动教育的开展,某学校在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为28米),用长为40米的篱笆,围成中间隔有一道篱笆的矩形菜地,在菜地的前端设计了两个宽1米的小门,便于同学们进入.
(1)若围成的菜地面积为120平方米,求此时边AB的长;
(2)可以围成的菜地面积最大是多少?
【点拨】(1)先由题意得到菜地的长AD为(40+2﹣3x)米,再列方程分情况讨论即可;
(2)设菜地的面积为S平方米,根据题意列出二次函数解析式,再根据二次函数的图象和性质作答即可.
【解析】解:(1)设菜地的宽AB为x米,
则菜地的长AD为(40+2﹣3x)米.
根据题意得x(40+2﹣3x)=120,
解得x1=4,x2=10,
当x=4时,40+2﹣3x=30>28,(不合题意,舍去);
当x=10时,40+2﹣3x=12<28,符合题意.
答:此时宽AB为10米;
(2)设菜地的面积为S平方米,则:
依题意得S=x(42﹣3x)=﹣3(x﹣7)2+147,
因为0<42﹣3x≤28,解得≤x<14;
当x=7时,S取最大值,此时S=147.
即菜地的最大面积为147平方米.
【点睛】本题考查了解一元二次方程和二次函数的图象和性质,解题时注意结果要符合题目要求.
23.在平面直角坐标系xOy中,点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上.设抛物线的对称轴为直线x=t.
(1)当t=2时,
①直接写出b与a满足的等量关系;
②比较m,n的大小,并说明理由;
(2)已知点C(x0,p)在该抛物线上,若对于3<x0<4,都有m>p>n,求t的取值范围.
【点拨】(1)①利用对称轴公式求得即可;
②利用二次函数的性质判断即可;
(2)由题意可知点A(﹣1,m)在对称轴的左侧,点B(3,n),C(x0,p)在对称轴的右侧,点A到对称轴的距离大于点C到对称轴的距离,据此即可得到,解得≤t≤3.
【解析】解:(1)①∵t=﹣=2,
∴b=﹣4a;
②∵抛物线y=ax2+bx+c中,a>0,
∴抛物线开口向上,
∵点A(﹣1,m),点B(3,n)在抛物线y=ax2+bx+c(a>0)上,对称轴为直线x=2,
∴点A(﹣1,m)到对称轴的距离大于点B(3,n)到对称轴的距离,
∴m>n;
(2)由题意可知,点A(﹣1,m)在对称轴的左侧,点B(3,n),C(x0,p)在对称轴的右侧,
∵3<x0<4,都有m>p>n,
∴点A到对称轴的距离大于点C到对称轴的距离,
∴,解得≤t≤3,
∴t的取值范围是≤t≤3.
【点睛】本题考查了二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的性质.
24.如图,AB为⊙O的直径,CD为⊙O的弦(不是直径),且CD⊥AB于点E,过点C作⊙O的直径CF,直线CB、DF交于点G.
(1)求证:△CFG为等腰三角形;
(2) ①若AB=6,求△CDF的最大面积;
②当∠ABC的度数为多少度时,以点B,O,D,F为顶点的四边形为菱形.
【点拨】(1)先判断出AB∥DG,进而得出∠ABC=∠G,再判断出∠ABC=∠BCF,即可得出结论;
(2)先判断出DH最大时,△CDF的面积最大,计算即可得出结论;
(3)先判断出△ODF是等边三角形,进而得出∠COD=120°,再用垂径定理,求出∠AOC即可得出结论.
【解析】解:(1)∵CF是⊙O的直径,
∴∠CDF=90°,
∵CD⊥AB,
∴∠BEC=90°=∠CDG,
∴AB∥DG,
∴∠ABC=∠G,
∵OB=OC,
∴∠ABC=∠BCF,
∴∠BCF=∠G,
∴CF=GF,
∴△CFG是等腰三角形;
(2)如图1,
过点D作DH⊥CF于H,
∵AB,CF都是⊙O直径,且AB=6,
∴CF=6,
∴S△CDF=CF×DH=3DH,
要S△CDF最大,则DH最大,而DH最大=3,
即:S△CDF最大=9,
(3)如图2,当点E在OA上时,
∵AB∥DG,∴要以点B,O,D,F为顶点的四边形为菱形,只有四边形BODF是菱形,
∴OD=DF,
∵OD=OF,
∴OD=OF=DF,
∴△ODF是等边三角形,
∴∠DOF=60°
∴∠COD=120°,
∵直径AB⊥CD,
∴∠AOC=COD=60°,
∴∠ABC=AOC=30°,
当点E在OB上时,同理:∠ABC=60°
即:当∠ABC的度数为30°或60°时,以点B,O,D,F为顶点的四边形为菱形,
【点睛】此题是圆的综合题,主要考查了圆的性质,垂径定理,圆周角定理,等腰三角形的判定和性质,等边三角形的判定和性质,菱形的性质,判断出AB∥DG是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
