内蒙古元宝山区平煤高级中学高中数学人教版必修二同步学案:1.2.2空间几何体的三视图
文档属性
| 名称 | 内蒙古元宝山区平煤高级中学高中数学人教版必修二同步学案:1.2.2空间几何体的三视图 |
|
|
| 格式 | zip | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-13 00:00:00 | ||
图片预览

文档简介
1.2.2空间几何体的三视图
学习目标
(1)理解三视图的含义,能画出简单几何体的三视图,掌握画法规则;
(2)能根据三视图,运用空间想象能力,识别并说出它所表示的空间图形.
学习过程
一、课前准备
1.预习教材的内容:
二、新课导学
(一) 基础知识
1.空间几何体的三视图是指 、 、 .
2.三视图的排列规则是 放在正视图的下方,长度与正视图一样, 放在正视图一样,宽度与俯视图的宽度一样.
3.三视图的正视图、俯视图、侧视图分别是从 、 、 观察同一个几何体,画出的空间几何体的图形.
(二) 典型例题
【例1】画出下列几何体的三视图.
(1)正方体 (2)圆锥
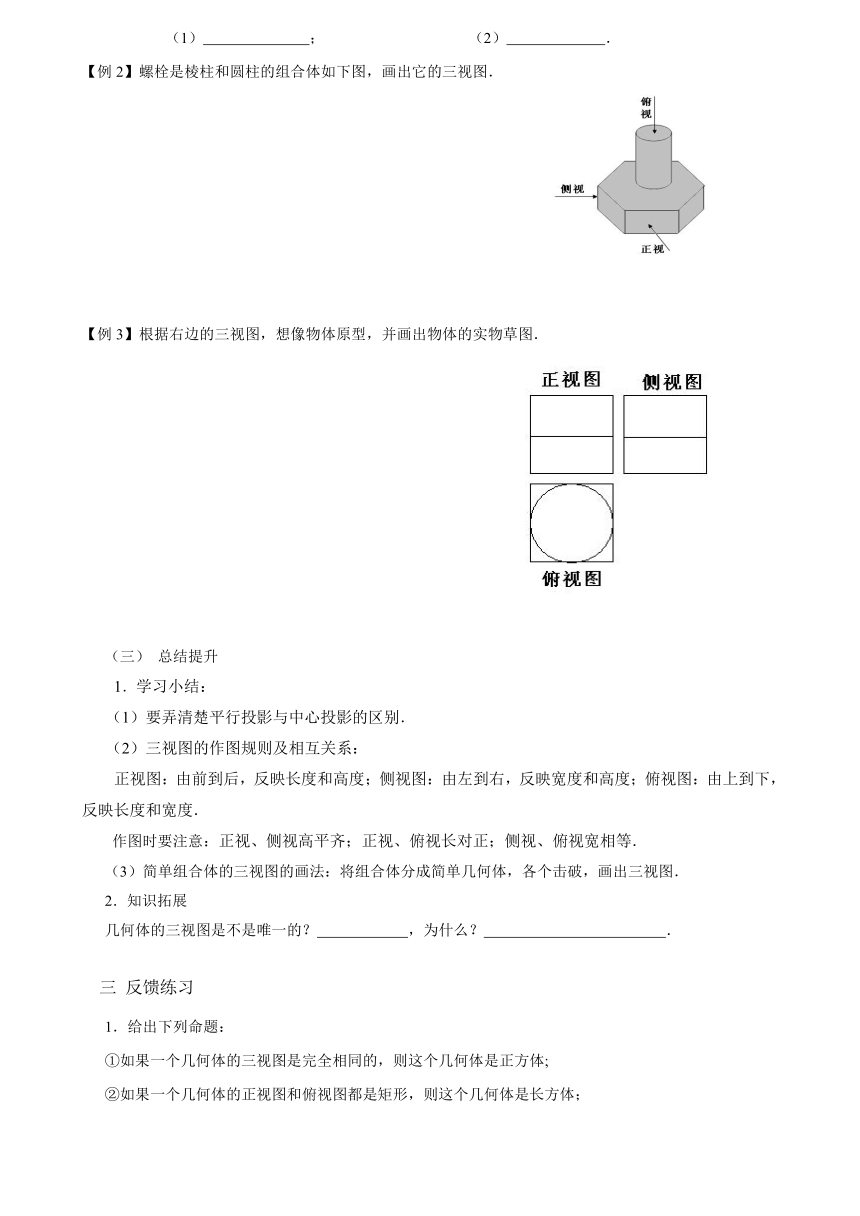
3.下列两个三视图对应的几何体是什么?
(1) ; (2) .
【例2】螺栓是棱柱和圆柱的组合体如下图,画出它的三视图.
【例3】根据右边的三视图,想像物体原型,并画出物体的实物草图.
(三) 总结提升
1.学习小结:
(1)要弄清楚平行投影与中心投影的区别.
(2)三视图的作图规则及相互关系:
正视图:由前到后,反映长度和高度;侧视图:由左到右,反映宽度和高度;俯视图:由上到下,反映长度和宽度.
作图时要注意:正视、侧视高平齐;正视、俯视长对正;侧视、俯视宽相等.
(3)简单组合体的三视图的画法:将组合体分成简单几何体,各个击破,画出三视图.
2.知识拓展
几何体的三视图是不是唯一的? ,为什么? .
三 反馈练习
1.给出下列命题:
①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;
②如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体;
③如果一个几何体的三视图都是矩形,则这个几何体是长方体;
④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
2.一个几何体的某一方向的视图是圆,则它不可能是( )
A.长方体 B.圆锥 C. 圆柱 D. 球体
3.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
4.如图,图(1)、(2)、(3)是图(4)所表示的几何体的三视图,其中图(1)是 ,图(2)是 ,图(3)是 。(说出视图名称)
5.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )
A.8 B.7 C.6 D.5
6.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥
C.四棱台 D.三棱台
7.下面三视图的实物图形的名称是 .
8.一个几何体的三视图中,正视图、俯视图一样,那么这个几何体是 (写出三种符合情况的几何体的名称).
学习目标
(1)理解三视图的含义,能画出简单几何体的三视图,掌握画法规则;
(2)能根据三视图,运用空间想象能力,识别并说出它所表示的空间图形.
学习过程
一、课前准备
1.预习教材的内容:
二、新课导学
(一) 基础知识
1.空间几何体的三视图是指 、 、 .
2.三视图的排列规则是 放在正视图的下方,长度与正视图一样, 放在正视图一样,宽度与俯视图的宽度一样.
3.三视图的正视图、俯视图、侧视图分别是从 、 、 观察同一个几何体,画出的空间几何体的图形.
(二) 典型例题
【例1】画出下列几何体的三视图.
(1)正方体 (2)圆锥
3.下列两个三视图对应的几何体是什么?
(1) ; (2) .
【例2】螺栓是棱柱和圆柱的组合体如下图,画出它的三视图.
【例3】根据右边的三视图,想像物体原型,并画出物体的实物草图.
(三) 总结提升
1.学习小结:
(1)要弄清楚平行投影与中心投影的区别.
(2)三视图的作图规则及相互关系:
正视图:由前到后,反映长度和高度;侧视图:由左到右,反映宽度和高度;俯视图:由上到下,反映长度和宽度.
作图时要注意:正视、侧视高平齐;正视、俯视长对正;侧视、俯视宽相等.
(3)简单组合体的三视图的画法:将组合体分成简单几何体,各个击破,画出三视图.
2.知识拓展
几何体的三视图是不是唯一的? ,为什么? .
三 反馈练习
1.给出下列命题:
①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;
②如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体;
③如果一个几何体的三视图都是矩形,则这个几何体是长方体;
④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
2.一个几何体的某一方向的视图是圆,则它不可能是( )
A.长方体 B.圆锥 C. 圆柱 D. 球体
3.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
4.如图,图(1)、(2)、(3)是图(4)所表示的几何体的三视图,其中图(1)是 ,图(2)是 ,图(3)是 。(说出视图名称)
5.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )
A.8 B.7 C.6 D.5
6.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥
C.四棱台 D.三棱台
7.下面三视图的实物图形的名称是 .
8.一个几何体的三视图中,正视图、俯视图一样,那么这个几何体是 (写出三种符合情况的几何体的名称).
