2016春九年级数学冀教版下册:29.1 点和圆的位置关系(共28张PPT)
文档属性
| 名称 | 2016春九年级数学冀教版下册:29.1 点和圆的位置关系(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 446.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-13 09:59:19 | ||
图片预览




文档简介
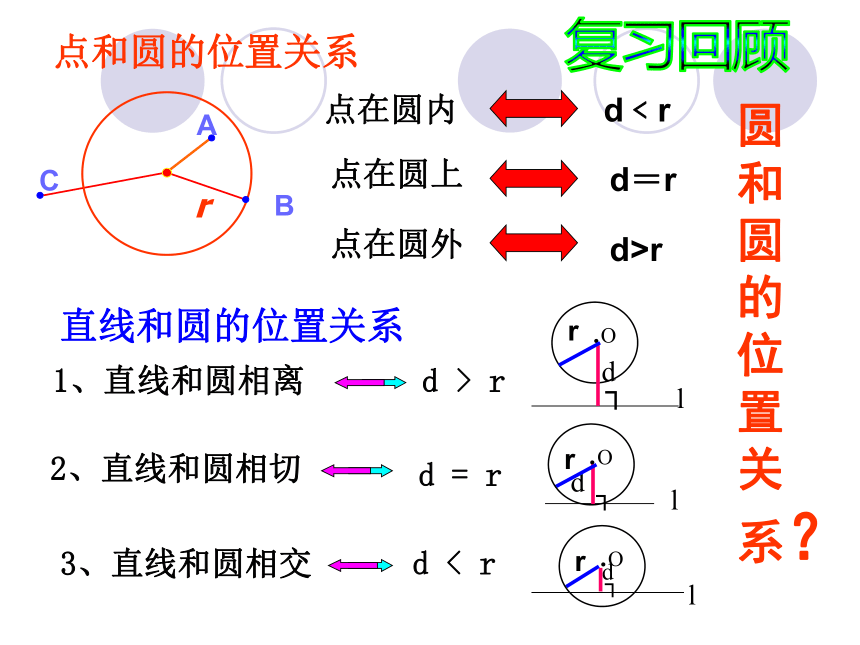
课件28张PPT。点和圆的位置关系复习回顾直线和圆的位置关系2、直线和圆相切d = r3、直线和圆相交d < r1、直线和圆相离d > r圆和圆的位置关系?(一):看一看(五)说一说
根据自己的亲身体验,总结圆与圆的位置关系两圆的位置关系相切相交相离外离内含外切内切相交(六).分一分:(根据两圆公共点的个数)(0个)(1个)(2个)提问:直线和圆有几种位置关系?
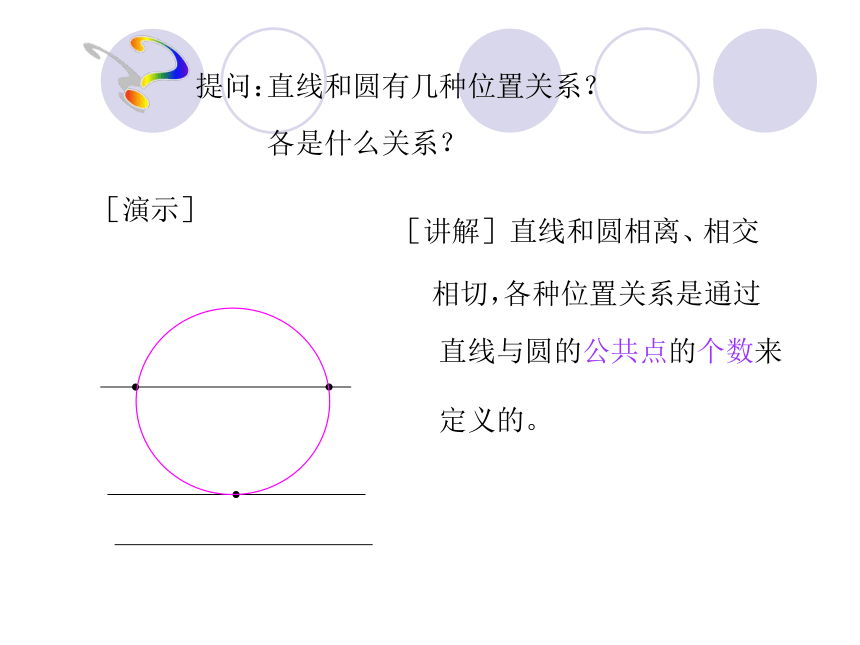
各是什么关系?[演示][讲解]直线和圆相离、相交相切,各种位置关系是通过直线与圆的公共点的个数来
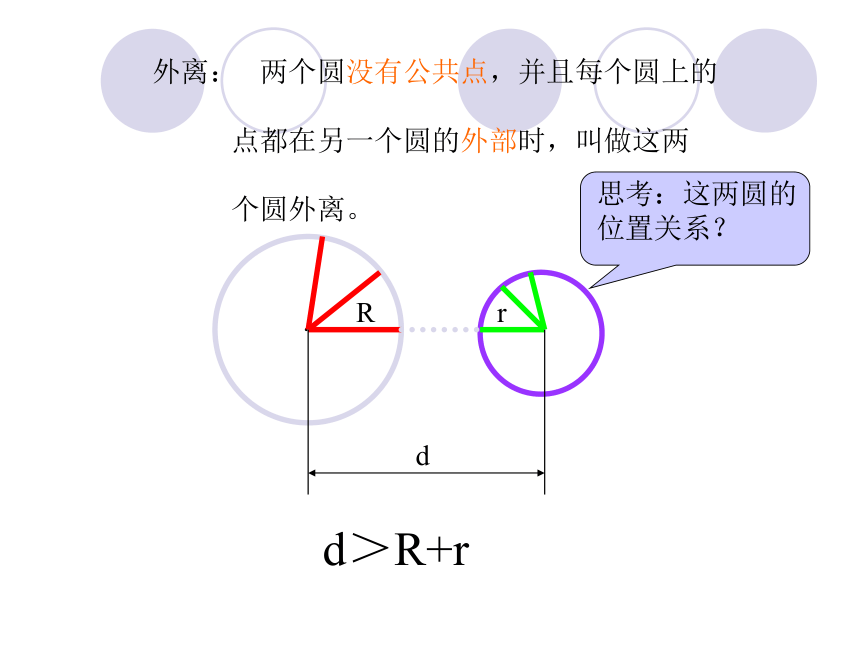
定义的。????提问:平面内的两个圆平移时,两圆有几个交点?演示:?没有交点有一个交点有两个交点有一个交点没有交点 两个圆没有公共点,并且每个圆上的
点都在另一个圆的外部时,叫做这两
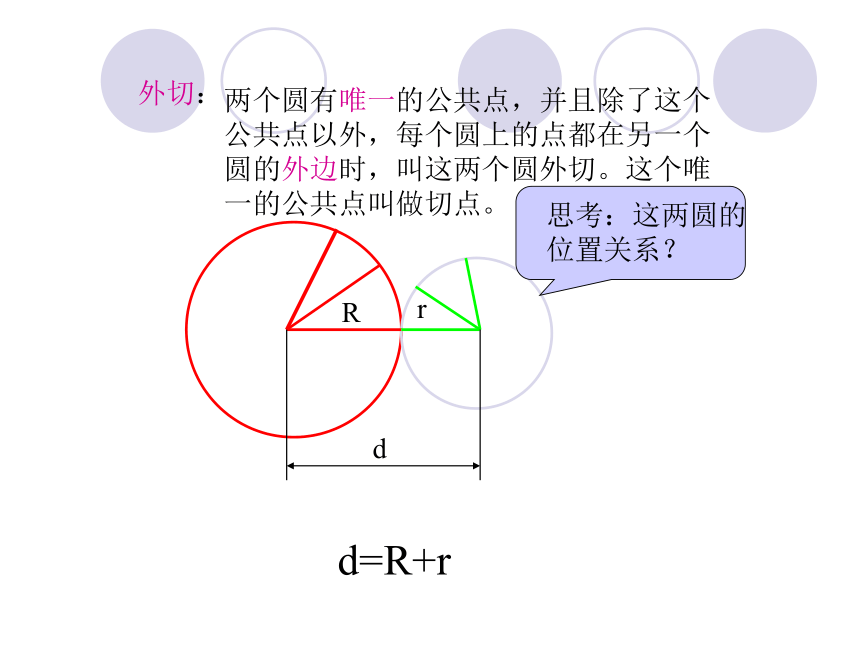
个圆外离。外离:dRrd>R+r 外切:两个圆有唯一的公共点,并且除了这个
公共点以外,每个圆上的点都在另一个
圆的外边时,叫这两个圆外切。这个唯
一的公共点叫做切点。dRrd=R+r两个圆有两个公共点,
此时叫做这两个圆相交。相交:dd<R+r两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。内切:dd=R-r两个圆没有公共点,并且一个
圆上的点在另一个圆的内部时
叫做这两个圆内含。内含:dd<R-r归纳小结观察:两圆相切有什么性质?通过两圆圆心的直线折叠后,
连心线与切点的关系如何?[提问]:O2 O1结论:相切两圆成轴对称图形,两圆圆心
的直线叫连心线是它们的对称轴。
如果两圆相切,那么切点一定在连心线上。???提问:两圆相交时,它们的数量关系如何?两圆两种数量关系用数轴表示:(R>或=r)例题分析,课堂练习例 如图(1),⊙O的半径为5厘米,点p是圆外一点,
op=8厘米。
求:(1)以p为圆心作⊙P与⊙O外切,小圆p的半径
是多少??d?练习1、 相切(内切)相离(外离)相交相离(内含)相切(外切)同心圆那么它们有怎样的位置关系?练习2
定圆O的半径是4厘米,动圆P的半径为1厘米。
(1)设圆P和圆O外切,那么点P和O的距离是多少?
点P可以在什么样的线上移动?解:OP=4+1=5厘米;点P可以在圆心P 和圆心O的连线上移动。(2)设圆O和圆P相内切,情况怎样?解:OP=4-1=3厘米;返回点P可以在圆心P 和圆心O的连线上移动。(1)对于圆与圆的位置关系,
我们是怎样判别的?(2)两圆的五种位置关系?(3)相切两圆圆心线
的性质?(4)注意圆心距和
两圆半径的数量
关系。返回四、小结六作业、1、设圆O1和圆O2的半径分别
为R、r,圆心距为d. 在下列情况
下,圆O1和圆O2的关系怎样?2、三角形的三边长分
别为4cm、5cm、6cm,
以各顶点为圆心的三
个圆两两外切。求各
圆的半径。3、画三个半径分别为
2cm、5cm、2.5cm的圆,
使它们两两外切。例1:圆O1和圆O2的半径分别为3厘米和4厘米,下列情况下两圆的位置关系是怎样? 相切(外切)相切(内切)(1)O1 O2=7厘米(2)O1 O2=1厘米 例2:圆O1和圆O2相切,圆O1的半径为3厘米,
圆心距d=8,则圆O2的半径为多少?
当外切时,R=5
当内切时,R=11
例3:两个同样大小的肥皂泡黏在一起,其剖面如左图所示,分隔两个肥皂泡的肥皂膜PQ成一条直线,TP,NP分别为两圆的切线,求∠TPN的大小.∵PO1= O1O2 =PO2
∴△PO1O2是一个等边三角形
∴ ∠ O1PO2= 60o,
又∵TP, NP 分别为两圆的切线∴ ∠ TPO1= 90o, ∠ NPO2= 90o, ∠ TPN= 360o- 90o- 90o - 60o= 120o2、⊙O1、⊙O2的半径分别为3㎝和2㎝的两圆相交,则圆心距d的取值范围为_________ 3、若相切的两圆直径分别为8㎝和14㎝,
则圆心距d为_________ 练习1、已知⊙O的半径为5㎝,⊙O1的半径为3㎝,
两圆的圆心距为7㎝,则它们的位置关系为___。4、若相切的两圆半径分别为8㎝和X㎝,
圆心距为3,则X的值为_________ 5、⊙O1、⊙O2的半径分别为2㎝和4㎝,连
心线O1 O2的长度在__________范围时,两圆无公共点。6、已知⊙O1、⊙O2、⊙O3两两外切,且半
径分别为2㎝、3㎝、10㎝,则△O1 O2 O3
的形状是_________。7、△ABC中,AB=8㎝,AC=7㎝,BC=5㎝,
以A、B、C为圆心的三个圆两两外切,则
⊙A、⊙B、⊙C的半径分别为__________。练习8、如果两圆半径恰好是方程的两根,圆心距d=3,则两圆的位置关系是_______。 9、已知⊙O1,⊙O2的半径分别为R、r ,且R>r,圆心距为d, 关于x的方程有两个相等的实数根,则两圆的位置是_____ 练习10、⊙O1与⊙O2相交,圆心距d为5㎝,⊙O1的
半径r1为3㎝,⊙O2的半径r2的取值范围为____。练习圆和圆的五种位置关系(1)相离(3)相交(2)相切外切外离内含内切两个公共点有一个公共点没有公共点d>R+rR-r(1)以P为圆心,作⊙P与⊙O外切
(2)以P为圆心,作⊙P与⊙O内切。
2.作三个半径分别为1cm、2cm、3cm的圆,使 它们两两相切。
根据自己的亲身体验,总结圆与圆的位置关系两圆的位置关系相切相交相离外离内含外切内切相交(六).分一分:(根据两圆公共点的个数)(0个)(1个)(2个)提问:直线和圆有几种位置关系?
各是什么关系?[演示][讲解]直线和圆相离、相交相切,各种位置关系是通过直线与圆的公共点的个数来
定义的。????提问:平面内的两个圆平移时,两圆有几个交点?演示:?没有交点有一个交点有两个交点有一个交点没有交点 两个圆没有公共点,并且每个圆上的
点都在另一个圆的外部时,叫做这两
个圆外离。外离:dRrd>R+r 外切:两个圆有唯一的公共点,并且除了这个
公共点以外,每个圆上的点都在另一个
圆的外边时,叫这两个圆外切。这个唯
一的公共点叫做切点。dRrd=R+r两个圆有两个公共点,
此时叫做这两个圆相交。相交:dd<R+r两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。内切:dd=R-r两个圆没有公共点,并且一个
圆上的点在另一个圆的内部时
叫做这两个圆内含。内含:dd<R-r归纳小结观察:两圆相切有什么性质?通过两圆圆心的直线折叠后,
连心线与切点的关系如何?[提问]:O2 O1结论:相切两圆成轴对称图形,两圆圆心
的直线叫连心线是它们的对称轴。
如果两圆相切,那么切点一定在连心线上。???提问:两圆相交时,它们的数量关系如何?两圆两种数量关系用数轴表示:(R>或=r)例题分析,课堂练习例 如图(1),⊙O的半径为5厘米,点p是圆外一点,
op=8厘米。
求:(1)以p为圆心作⊙P与⊙O外切,小圆p的半径
是多少??d?练习1、 相切(内切)相离(外离)相交相离(内含)相切(外切)同心圆那么它们有怎样的位置关系?练习2
定圆O的半径是4厘米,动圆P的半径为1厘米。
(1)设圆P和圆O外切,那么点P和O的距离是多少?
点P可以在什么样的线上移动?解:OP=4+1=5厘米;点P可以在圆心P 和圆心O的连线上移动。(2)设圆O和圆P相内切,情况怎样?解:OP=4-1=3厘米;返回点P可以在圆心P 和圆心O的连线上移动。(1)对于圆与圆的位置关系,
我们是怎样判别的?(2)两圆的五种位置关系?(3)相切两圆圆心线
的性质?(4)注意圆心距和
两圆半径的数量
关系。返回四、小结六作业、1、设圆O1和圆O2的半径分别
为R、r,圆心距为d. 在下列情况
下,圆O1和圆O2的关系怎样?2、三角形的三边长分
别为4cm、5cm、6cm,
以各顶点为圆心的三
个圆两两外切。求各
圆的半径。3、画三个半径分别为
2cm、5cm、2.5cm的圆,
使它们两两外切。例1:圆O1和圆O2的半径分别为3厘米和4厘米,下列情况下两圆的位置关系是怎样? 相切(外切)相切(内切)(1)O1 O2=7厘米(2)O1 O2=1厘米 例2:圆O1和圆O2相切,圆O1的半径为3厘米,
圆心距d=8,则圆O2的半径为多少?
当外切时,R=5
当内切时,R=11
例3:两个同样大小的肥皂泡黏在一起,其剖面如左图所示,分隔两个肥皂泡的肥皂膜PQ成一条直线,TP,NP分别为两圆的切线,求∠TPN的大小.∵PO1= O1O2 =PO2
∴△PO1O2是一个等边三角形
∴ ∠ O1PO2= 60o,
又∵TP, NP 分别为两圆的切线∴ ∠ TPO1= 90o, ∠ NPO2= 90o, ∠ TPN= 360o- 90o- 90o - 60o= 120o2、⊙O1、⊙O2的半径分别为3㎝和2㎝的两圆相交,则圆心距d的取值范围为_________ 3、若相切的两圆直径分别为8㎝和14㎝,
则圆心距d为_________ 练习1、已知⊙O的半径为5㎝,⊙O1的半径为3㎝,
两圆的圆心距为7㎝,则它们的位置关系为___。4、若相切的两圆半径分别为8㎝和X㎝,
圆心距为3,则X的值为_________ 5、⊙O1、⊙O2的半径分别为2㎝和4㎝,连
心线O1 O2的长度在__________范围时,两圆无公共点。6、已知⊙O1、⊙O2、⊙O3两两外切,且半
径分别为2㎝、3㎝、10㎝,则△O1 O2 O3
的形状是_________。7、△ABC中,AB=8㎝,AC=7㎝,BC=5㎝,
以A、B、C为圆心的三个圆两两外切,则
⊙A、⊙B、⊙C的半径分别为__________。练习8、如果两圆半径恰好是方程的两根,圆心距d=3,则两圆的位置关系是_______。 9、已知⊙O1,⊙O2的半径分别为R、r ,且R>r,圆心距为d, 关于x的方程有两个相等的实数根,则两圆的位置是_____ 练习10、⊙O1与⊙O2相交,圆心距d为5㎝,⊙O1的
半径r1为3㎝,⊙O2的半径r2的取值范围为____。练习圆和圆的五种位置关系(1)相离(3)相交(2)相切外切外离内含内切两个公共点有一个公共点没有公共点d>R+rR-r
(2)以P为圆心,作⊙P与⊙O内切。
2.作三个半径分别为1cm、2cm、3cm的圆,使 它们两两相切。
