2016春九年级数学冀教版下册:30.2 二次函数的图像和性质(共13张PPT)
文档属性
| 名称 | 2016春九年级数学冀教版下册:30.2 二次函数的图像和性质(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 399.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-13 18:50:03 | ||
图片预览




文档简介
课件13张PPT。二次函数的图像和性质教学目标:
1 会用描点法画出二次函数 的图像
2 会说出二次函数图像 的开口方向,对称轴,顶点坐标
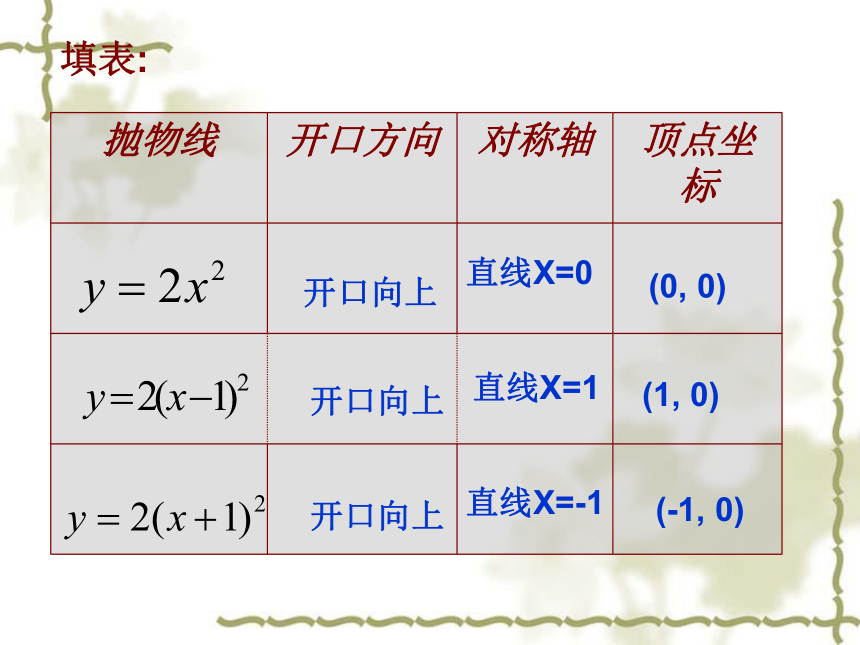
3 培养学生经历由具体到一般的探索事物的规律的过程复习归纳:完成下列两表开口向下开口向下开口向下直线X=0(0,0) (0,1) (0,-1)填表直线X=0直线X=0填表:开口向上开口向上开口向上直线X=0直线X=1直线X=-1(0, 0)(1, 0)(-1, 0)新课讲授:操作题1:在同一坐标系内,画出函数
的图像.指导:(1) 列表时,要合理取值,首先考虑对称性,其次尽量取整
(2)描点时,一般先定顶点,然后根据对称性,描出对称点
(3)连线时,注意顶点附近的大致走向,画出的抛物线应平滑,对称,且符合抛物线的特点
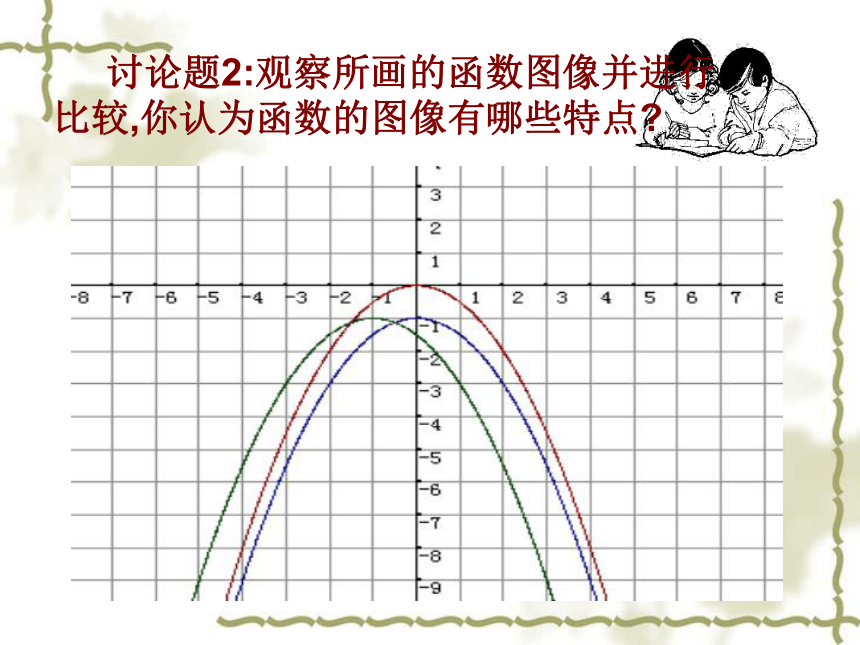
(4)对描点,连线中出现的误差,要适当修正,或修正不合适的选值. 讨论题2:观察所画的函数图像并进行比较,你认为函数的图像有哪些特点?的图像可以由向下平移一个单位向左平移一个单位向左平移一个单位向下平移
一个单位先向下平移一个单位,再向左平移一个单位,或者先向左平移一个单位再向下平移一个单位而得到. 归纳总结:
图像的特点. (1)a的符号决定抛物线的开口方向的图像性质:(2)对称轴是直线x=h(3)顶点坐标是(h,k)图像的性质:开口向下,对称轴是x=-1,顶点坐标是(-1,-1)小练习:开口向上开口向上开口向上开口向上开口向上开口向下开口向下直线x=0直线x=0直线x=-1直线x=1直线x=-1直线x=-1直线x=h(0,0)(0,2)(-1,0)(1,-2)(-1,-2)(-1,2)(h,k)例题分析:
一条抛物线的形状与抛物线
相同,其顶点坐标是(-1,3),写出这个抛物线的解析式.解:设函数解析式为又因为所求抛物线顶点坐标是(-1,3),所以h=-1,k=3所以这个函数的解析式为:即:拓展:如果给我们的函数形式是: 因为所求抛物线的形状与
相同,所以a=-2.图像如何画?相应练习: 一条抛物线的形状与抛物线
相同,其对称轴与抛物线
相同,且顶点的纵坐标是4,写出这条抛物
线的解析式.小结:
本节课主要运用了数形结合的思想方法,通过对函数图象的讨论,分析归纳出 的性质:(1)a的符号决定抛物线的开口方向(2)对称轴是直线x=h(3)顶点坐标是(h,k)开口向上 开口向上 开口向上直线X=0 直线X=h直线X=h(0,k)(h,0)(h,k)作业:
1 会用描点法画出二次函数 的图像
2 会说出二次函数图像 的开口方向,对称轴,顶点坐标
3 培养学生经历由具体到一般的探索事物的规律的过程复习归纳:完成下列两表开口向下开口向下开口向下直线X=0(0,0) (0,1) (0,-1)填表直线X=0直线X=0填表:开口向上开口向上开口向上直线X=0直线X=1直线X=-1(0, 0)(1, 0)(-1, 0)新课讲授:操作题1:在同一坐标系内,画出函数
的图像.指导:(1) 列表时,要合理取值,首先考虑对称性,其次尽量取整
(2)描点时,一般先定顶点,然后根据对称性,描出对称点
(3)连线时,注意顶点附近的大致走向,画出的抛物线应平滑,对称,且符合抛物线的特点
(4)对描点,连线中出现的误差,要适当修正,或修正不合适的选值. 讨论题2:观察所画的函数图像并进行比较,你认为函数的图像有哪些特点?的图像可以由向下平移一个单位向左平移一个单位向左平移一个单位向下平移
一个单位先向下平移一个单位,再向左平移一个单位,或者先向左平移一个单位再向下平移一个单位而得到. 归纳总结:
图像的特点. (1)a的符号决定抛物线的开口方向的图像性质:(2)对称轴是直线x=h(3)顶点坐标是(h,k)图像的性质:开口向下,对称轴是x=-1,顶点坐标是(-1,-1)小练习:开口向上开口向上开口向上开口向上开口向上开口向下开口向下直线x=0直线x=0直线x=-1直线x=1直线x=-1直线x=-1直线x=h(0,0)(0,2)(-1,0)(1,-2)(-1,-2)(-1,2)(h,k)例题分析:
一条抛物线的形状与抛物线
相同,其顶点坐标是(-1,3),写出这个抛物线的解析式.解:设函数解析式为又因为所求抛物线顶点坐标是(-1,3),所以h=-1,k=3所以这个函数的解析式为:即:拓展:如果给我们的函数形式是: 因为所求抛物线的形状与
相同,所以a=-2.图像如何画?相应练习: 一条抛物线的形状与抛物线
相同,其对称轴与抛物线
相同,且顶点的纵坐标是4,写出这条抛物
线的解析式.小结:
本节课主要运用了数形结合的思想方法,通过对函数图象的讨论,分析归纳出 的性质:(1)a的符号决定抛物线的开口方向(2)对称轴是直线x=h(3)顶点坐标是(h,k)开口向上 开口向上 开口向上直线X=0 直线X=h直线X=h(0,k)(h,0)(h,k)作业:
