第21-23章 旋转 复习卷 (含详解) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第21-23章 旋转 复习卷 (含详解) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 470.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 20:08:24 | ||
图片预览




文档简介
第21-23章复习卷-2024-2025学年数学九年级上册人教版
一.选择题(共9小题)
1.(2024秋 临潼区期中)下列字母既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(2024秋 崂山区期中)若一元二次方程3x2=5x+2的二次项系数是3,则它的常数项是( )
A.﹣2 B.2 C.﹣5 D.5
3.(2024秋 新会区校级月考)方程(x+1)(x﹣1)=0的根是( )
A.x1=x2=1 B.x1=1,x2=﹣1
C.x1=x2=﹣1 D.x1=1,x2=0
4.(2024秋 青山区期中)有一个人患了流感,经过两轮传染后,共有81个人患了流感,设平均每轮每人传染x个人,则下列等式成立的是( )
A.1+x+x2=81 B.1+x+x(x+1)=81
C.1+x+(1+x)2=81 D.1+(1+x)2=81
5.(2024秋 大兴区期中)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,则∠B1度数为( )
A.29° B.32° C.58° D.61°
6.(2024秋 铁西区校级月考)如图,直线a∥b,△AOB的边OB在直线b上,∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1为( )
A.50° B.55° C.60° D.75°
7.(2024秋 信阳期中)关于x的二次函数y=(a+1)x2+ax+2a2﹣2的图象过原点,则a的值为( )
A.﹣1 B.1 C.±1 D.0
8.(2024秋 开鲁县校级期中)关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下
B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小
D.图象的顶点坐标为(﹣3,﹣2)
9.(2024秋 南开区期中)二次函数y=ax2+bx+c(a≠0)的图象开口向下,与x轴交于点(﹣3,0),其对称轴为直线,有下列结论:①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④对于任意非零实数m,若x1,x2(x1<x2)为方程a(x+3)(x﹣2)+m2=0的两个根,则x1<﹣3且x2>2.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共9小题)
10.(2024秋 朝阳区校级期中)若m、n是一元二次方程3x2﹣kx+2=0的两个根,则mn= .
11.(2024秋 大兴区期中)在平面直角坐标系xOy中,点(﹣2,3)关于原点的对称点坐标为 .
12.(2024秋 蓬江区校级期中)将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若AB=2,将三角板绕原点O逆时针旋转60°,则点A的对应点A′的坐标为 .
13.(2024秋 南开区期中)如图,Rt△ABC中,AB=8,BC=2,∠BCA=90°,将Rt△ABC绕着点A顺时针旋转,得到Rt△AB′C′,点B,C的对应点分别为B′,C′,连接CC′,交AB于点M,点M恰为AB边中点.
(Ⅰ)△AMC的面积为 ;
(Ⅱ)线段C′M的长为 .
14.(2024秋 建邺区期中)若关于x的方程x2﹣6x+m+1=0有两个不相等的实数根,则m的取值范围是 .
15.(2024秋 大兴区期中)某校生物学科老师在组织学生进行野外实践活动时,学生发现自然界的植物生长具有神奇的规律.比如某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,设这种植物每个支干长出的小分支个数为x,则可列方程为 .
16.(2024秋 大兴区期中)已知抛物线y=x2﹣4x+c与x轴没有交点,则实数c的取值范围是 .
17.(2024秋 崂山区期中)在正常情况下,10米跳台跳水运动员必须在距水面不小于5m时完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员距离水面的高度h(m)和运动员起跳后的运动时间t(s)之间满足关系:h=10+2.5t﹣5t2,则当h=5时,10+2.5t﹣5t2=5即2t2﹣t﹣2=0.
t 1.1 1.2 1.3 1.4
2t2﹣t﹣2 ﹣0.68 ﹣0.32 0.08 0.52
根据表格中的对应值,可判断运动员完成动作的时间最多不超过 s.(精确到0.1)
18.(2024秋 信阳期中)定义:由a,b构造的二次函数y=ax2+(a﹣b)x﹣b叫作一次函数y=ax﹣b的“滋生函数”,一次函数y=ax﹣b叫作二次函数y=ax2+(a﹣b)x﹣b的“本源函数”(a,b为常数,且a≠0).若一次函数y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,则二次函数y=ax2﹣4x+a+2的“本源函数”是 .
三.解答题(共8小题)
19.(2024秋 昂仁县期中)解方程:
(1)x2﹣4x+3=0;
(2)1﹣8x+16x2=2﹣8x;
(3)(x﹣2)2+x(x﹣2)=0.
20.(2024秋 建邺区期中)关于x的一元二次方程mx2+nx+2=0.
(1)求证:当n=m+2时,此方程必有实数根;
(2)若方程有两个相等的整数根,写出满足条件的一组m,n的值,并求此时方程的根.
21.(2024秋 浦北县期中)如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的三个顶点均在格点上.
(1)将△ABC向x轴正方向平移5个单位长度得到△A1B1C1,画出△A1B1C1;
(2)在(1)的条件下,以点O为中心,将△A1B1C1旋转180°得△A2B2C2,画出△A2B2C2.
22.(2024秋 崂山区期中)面向日益严峻的气候变化形势,以发展新能源汽车推动道路交通领域零碳转型已成为全球共识.我国政府不断加大对新能源汽车的支持和推动,新能源汽车的市场需求正在不断增加.如表是一款某品牌新能源热门车型7月份和9月份的全国销量情况:
月份 7月 9月
销量/万辆 2.5 3.6
(1)求该款车销量的月平均增长率.
(2)青岛一个该品牌4S店购进一批该款车型进行销售,已知进价为每辆6万元.经试销发现:当该款汽车售价为7.5万元时,平均每月销量为150辆;而当售价每降低0.1万元时,平均每月就能多售出15辆.为了扩大销量,该4S店决定降价促销,若该4S店想要维持利润不变,该款车的售价应为每辆多少万元?
23.(2024秋 安定区期中)已知抛物线y=x2+bx+c过(0,8),(6,8)两点.
(1)求出该抛物线的解析式;
(2)求出抛物线与x轴的交点坐标;
(3)当y<0时,写出x的取值范围.
24.(2024秋 大兴区期中)已知,△ABC是等腰三角形,∠BAC=60°,O是△ABC内的任意一点,连接OA,OB,OC.
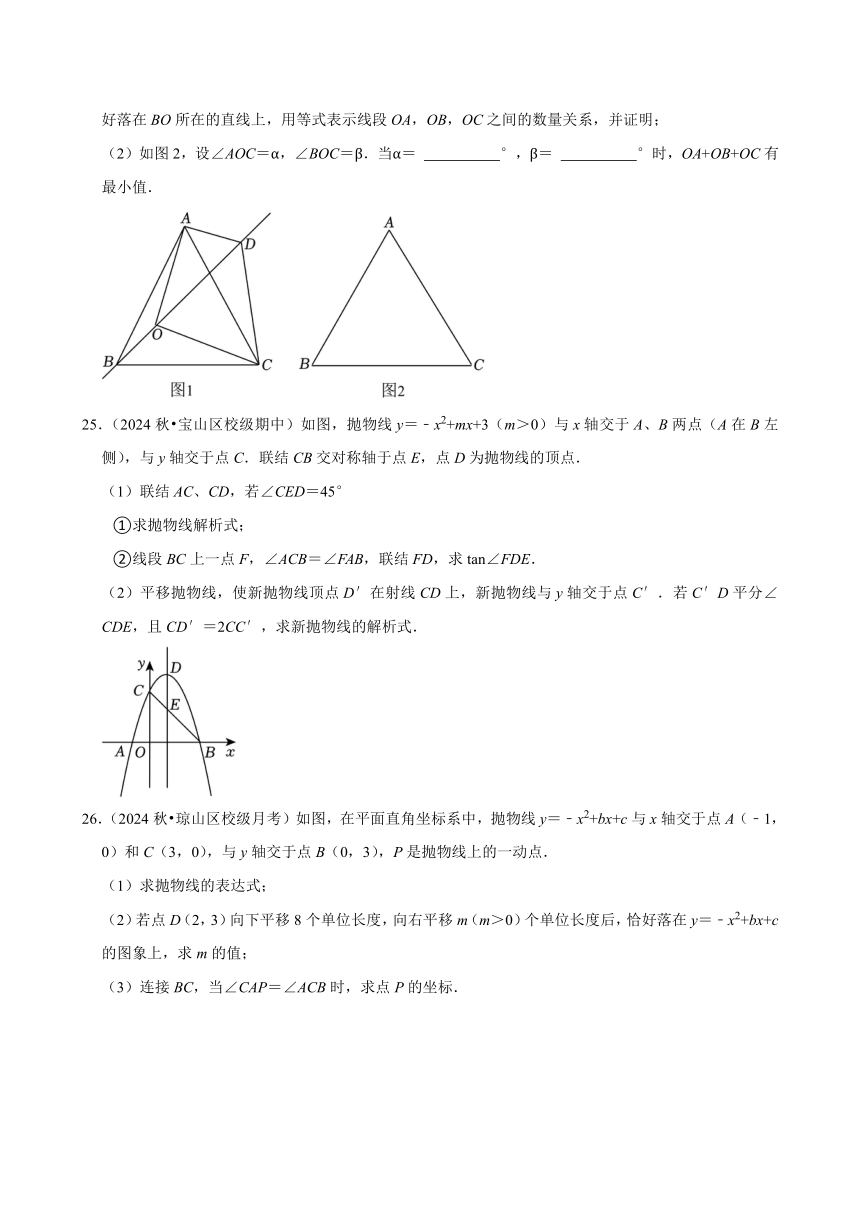
(1)如图1,∠AOC=90°,∠BOC=120°,将△BOC绕点C顺时针旋转60°得到△ADC.点D恰好落在BO所在的直线上,用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)如图2,设∠AOC=α,∠BOC=β.当α= °,β= °时,OA+OB+OC有最小值.
25.(2024秋 宝山区校级期中)如图,抛物线y=﹣x2+mx+3(m>0)与x轴交于A、B两点(A在B左侧),与y轴交于点C.联结CB交对称轴于点E,点D为抛物线的顶点.
(1)联结AC、CD,若∠CED=45°
①求抛物线解析式;
②线段BC上一点F,∠ACB=∠FAB,联结FD,求tan∠FDE.
(2)平移抛物线,使新抛物线顶点D′在射线CD上,新抛物线与y轴交于点C′.若C′D平分∠CDE,且CD′=2CC′,求新抛物线的解析式.
26.(2024秋 琼山区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和C(3,0),与y轴交于点B(0,3),P是抛物线上的一动点.
(1)求抛物线的表达式;
(2)若点D(2,3)向下平移8个单位长度,向右平移m(m>0)个单位长度后,恰好落在y=﹣x2+bx+c的图象上,求m的值;
(3)连接BC,当∠CAP=∠ACB时,求点P的坐标.
第21-23章复习卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
一.选择题(共9小题)
1.(2024秋 临潼区期中)下列字母既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解答】解:A.“H”既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.“S”不是轴对称图形,是中心对称图形,故本选项不符合题意;
C.“A”是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.“Q”既不是轴对称图形,也不是中心对称图形,故本选项不符合题意.
故选:A.
2.(2024秋 崂山区期中)若一元二次方程3x2=5x+2的二次项系数是3,则它的常数项是( )
A.﹣2 B.2 C.﹣5 D.5
【解答】解:方程3x2=5x+2,
整理得:3x2﹣5x﹣2=0,
则常数项是﹣2.
故选:A.
3.(2024秋 新会区校级月考)方程(x+1)(x﹣1)=0的根是( )
A.x1=x2=1 B.x1=1,x2=﹣1
C.x1=x2=﹣1 D.x1=1,x2=0
【解答】解:∵(x+1)(x﹣1)=0,
∴x﹣1=0或x+1=0,
解得x1=1,x2=﹣1,
故选:B.
4.(2024秋 青山区期中)有一个人患了流感,经过两轮传染后,共有81个人患了流感,设平均每轮每人传染x个人,则下列等式成立的是( )
A.1+x+x2=81 B.1+x+x(x+1)=81
C.1+x+(1+x)2=81 D.1+(1+x)2=81
【解答】解:依题意得1+x+x(x+1)=81.
故选:B.
5.(2024秋 大兴区期中)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,则∠B1度数为( )
A.29° B.32° C.58° D.61°
【解答】解:∵将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,
∴AC=A1C,∠ACA1=58°,∠B=∠B1,
∴∠A=∠AA1C=(180°﹣58°)=61°,
∵∠ACB=90°,
∴∠B=90°﹣61°=29°,
∴∠B1=∠B=29°,
故选:A.
6.(2024秋 铁西区校级月考)如图,直线a∥b,△AOB的边OB在直线b上,∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1为( )
A.50° B.55° C.60° D.75°
【解答】解:如图:
由题意可得:∠A1OB1=∠AOB=55°,∠AOA1=75°,
∴∠A1OD=180°﹣55°﹣75°=50°,
∵直线a∥b,
∴∠1=∠A1OD=50°,
故选:A.
7.(2024秋 信阳期中)关于x的二次函数y=(a+1)x2+ax+2a2﹣2的图象过原点,则a的值为( )
A.﹣1 B.1 C.±1 D.0
【解答】解:把(0,0)代入y=(a+1)x2+3x+a2﹣1得a2﹣1=0,
解得a=1或a=﹣1,
而a+1≠0,
所以a的值为1.
故选:B.
8.(2024秋 开鲁县校级期中)关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下
B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小
D.图象的顶点坐标为(﹣3,﹣2)
【解答】解:∵二次函数,a=<0,
∴开口向下,顶点坐标为(3,﹣2);当x=3时,y有最大值﹣2;当x>3时,y随x的增大而减小;图象的顶点坐标为(3,﹣2);
∴D选项错误,符合题意,
故选:D.
9.(2024秋 南开区期中)二次函数y=ax2+bx+c(a≠0)的图象开口向下,与x轴交于点(﹣3,0),其对称轴为直线,有下列结论:①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④对于任意非零实数m,若x1,x2(x1<x2)为方程a(x+3)(x﹣2)+m2=0的两个根,则x1<﹣3且x2>2.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线与x轴交于点(﹣3,0),对称轴为直线,
∴抛物线与x轴的另一个交点为(2,0),
∴抛物线与y轴交于正半轴,
∴c>0,
∵﹣=﹣,
∴a=b,
∴abc>0,故①正确;
∵抛物线解析式为y=ax2+ax+c经过(﹣3,0),
∴9a﹣3a+c=0,
∴6a+c=0,
∴3a+3a+c=0,
∵3a<0,
∴3a+c>0,故②正确;
∵当x>﹣时,y随x的增大而减小,故③错误;
由题意x1,x2(x1<x2)是抛物线y=a(x+3)(x﹣2)与直线y=﹣m2交点的横坐标,
∴x1<﹣3,x2>2,故④正确.
故选:C.
二.填空题(共9小题)
10.(2024秋 朝阳区校级期中)若m、n是一元二次方程3x2﹣kx+2=0的两个根,则mn= .
【解答】解:∵m、n是一元二次方程3x2﹣kx+2=0的根,
∴mn=.
故答案为:.
11.(2024秋 大兴区期中)在平面直角坐标系xOy中,点(﹣2,3)关于原点的对称点坐标为 (2,﹣3) .
【解答】解:点(﹣2,3)关于原点O对称的点的坐标是:(2,﹣3).
故答案为:(2,﹣3).
12.(2024秋 蓬江区校级期中)将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若AB=2,将三角板绕原点O逆时针旋转60°,则点A的对应点A′的坐标为 (0) .
【解答】解:由题意得,将三角板绕原点O逆时针旋转60°,点A的对应点A′落在y轴的正半轴上.
在Rt△AOB中,∠AOB=30°,AB=2,
∴OA===,
∴OA'=OA=,
∴点A′的坐标为(0).
故答案为:(0).
13.(2024秋 南开区期中)如图,Rt△ABC中,AB=8,BC=2,∠BCA=90°,将Rt△ABC绕着点A顺时针旋转,得到Rt△AB′C′,点B,C的对应点分别为B′,C′,连接CC′,交AB于点M,点M恰为AB边中点.
(Ⅰ)△AMC的面积为 ;
(Ⅱ)线段C′M的长为 11 .
【解答】解:(1)∵AB=8,BC=2,∠BCA=90°,
∴AC===,
∴S△ABC===.
∵点M为AB边中点,
∴=.
故答案为:.
(2)过点A作AD⊥CC'于点D,
由旋转得,AC=AC',
∴△ACC'为等腰三角形,
∴CD=C'D.
∵点M为AB边中点,∠BCA=90°,
∴CM==AM=4,
∴∠ACM=∠CAM.
∵cos∠CAB==,
∴cos∠ACM==,
∴CD=,
∴CC'=2CD=15,
∴C'M=CC'﹣CM=15﹣4=11.
故答案为:11.
14.(2024秋 建邺区期中)若关于x的方程x2﹣6x+m+1=0有两个不相等的实数根,则m的取值范围是 m<8 .
【解答】解:根据题意得Δ=(﹣6)2﹣4×1×(m+1)>0,
解得m<8.
故答案为:m<8.
15.(2024秋 大兴区期中)某校生物学科老师在组织学生进行野外实践活动时,学生发现自然界的植物生长具有神奇的规律.比如某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,设这种植物每个支干长出的小分支个数为x,则可列方程为 x2+x+1=43 .
【解答】解:根据题意列方程得:x2+x+1=43.
故答案为:x2+x+1=43.
16.(2024秋 大兴区期中)已知抛物线y=x2﹣4x+c与x轴没有交点,则实数c的取值范围是 c>4 .
【解答】解:若抛物线y=x2﹣4x+c与x轴没有交点,则Δ=(﹣4)2﹣4c<0,
解得c>4.
故答案为:c>4.
17.(2024秋 崂山区期中)在正常情况下,10米跳台跳水运动员必须在距水面不小于5m时完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员距离水面的高度h(m)和运动员起跳后的运动时间t(s)之间满足关系:h=10+2.5t﹣5t2,则当h=5时,10+2.5t﹣5t2=5即2t2﹣t﹣2=0.
t 1.1 1.2 1.3 1.4
2t2﹣t﹣2 ﹣0.68 ﹣0.32 0.08 0.52
根据表格中的对应值,可判断运动员完成动作的时间最多不超过 1.3 s.(精确到0.1)
【解答】解:根据表格中的对应值,可判断运动员完成动作的时间最多不超过1.3s,
故答案为:1.3.
18.(2024秋 信阳期中)定义:由a,b构造的二次函数y=ax2+(a﹣b)x﹣b叫作一次函数y=ax﹣b的“滋生函数”,一次函数y=ax﹣b叫作二次函数y=ax2+(a﹣b)x﹣b的“本源函数”(a,b为常数,且a≠0).若一次函数y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,则二次函数y=ax2﹣4x+a+2的“本源函数”是 y=﹣3x﹣1 .
【解答】解:∵y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,
∴y=ax2﹣4x+a+2=ax2+(a﹣b)x﹣b,即,
解得,
∴y=ax2﹣4x+a+2的“本源函数”是y=﹣3x﹣1,
故答案为:y=﹣3x﹣1.
三.解答题(共8小题)
19.(2024秋 昂仁县期中)解方程:
(1)x2﹣4x+3=0;
(2)1﹣8x+16x2=2﹣8x;
(3)(x﹣2)2+x(x﹣2)=0.
【解答】解:(1)∵x2﹣4x+3=0,
∴(x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
解得x1=1,x2=3;
(2)1﹣8x+16x2=2﹣8x,
移项及合并同类项,得:16x2=1,
系数化为1,得:,
∴;
(3)∵(x﹣2)2+x(x﹣2)=0,
∴(x﹣2)(x﹣2+x)=0,
∴x﹣2=0或x﹣2+x=0,
解得x1=2,x2=1.
20.(2024秋 建邺区期中)关于x的一元二次方程mx2+nx+2=0.
(1)求证:当n=m+2时,此方程必有实数根;
(2)若方程有两个相等的整数根,写出满足条件的一组m,n的值,并求此时方程的根.
【解答】解:(1)∵Δ=n2﹣8m,
当n=m+2时,Δ=(m+2)2﹣8m=(m﹣2)2≥0,
∴方程必有实数根;
(2)∵方程有两个相等的整数根,
∴Δ=n2﹣8m=0,
若n=4,m=2,
则方程变形为2x2+4x+2=0,
解得x1=x2=﹣1.
21.(2024秋 浦北县期中)如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的三个顶点均在格点上.
(1)将△ABC向x轴正方向平移5个单位长度得到△A1B1C1,画出△A1B1C1;
(2)在(1)的条件下,以点O为中心,将△A1B1C1旋转180°得△A2B2C2,画出△A2B2C2.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
22.(2024秋 崂山区期中)面向日益严峻的气候变化形势,以发展新能源汽车推动道路交通领域零碳转型已成为全球共识.我国政府不断加大对新能源汽车的支持和推动,新能源汽车的市场需求正在不断增加.如表是一款某品牌新能源热门车型7月份和9月份的全国销量情况:
月份 7月 9月
销量/万辆 2.5 3.6
(1)求该款车销量的月平均增长率.
(2)青岛一个该品牌4S店购进一批该款车型进行销售,已知进价为每辆6万元.经试销发现:当该款汽车售价为7.5万元时,平均每月销量为150辆;而当售价每降低0.1万元时,平均每月就能多售出15辆.为了扩大销量,该4S店决定降价促销,若该4S店想要维持利润不变,该款车的售价应为每辆多少万元?
【解答】解:(1)设该款车销量的月平均增长率为x,
根据题意得:2.5(1+x)2=3.6,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:该款车销量的月平均增长率为20%;
(2)设该款车的售价为每辆y万元,则每辆的销售利润为(y﹣6)万元,平均每月可售出150+×15=(1275﹣150y)辆,
根据题意得:(y﹣6)(1275﹣150y)=(7.5﹣6)×150,
整理得:2y2﹣29y+105=0,
解得:y1=7,y2=7.5(不符合题意,舍去).
答:该款车的售价应为每辆7万元.
23.(2024秋 安定区期中)已知抛物线y=x2+bx+c过(0,8),(6,8)两点.
(1)求出该抛物线的解析式;
(2)求出抛物线与x轴的交点坐标;
(3)当y<0时,写出x的取值范围.
【解答】解:(1)∵抛物线y=x2+bx+c过(0,8),(6,8)两点,
∴
解得:
∴该抛物线的解析式为y=x2﹣6x+8;
(2)将y=0代入y=x2﹣6x+8,得x2﹣6x+8=0
解得:x1=2,x2=4
∴抛物线与x轴的交点坐标为(2,0)和(4,0);
(3)∵y=x2+bx+c中,a=1>0,其图象大致如下
由图象可知:当y<0时,2<x<4.
24.(2024秋 大兴区期中)已知,△ABC是等腰三角形,∠BAC=60°,O是△ABC内的任意一点,连接OA,OB,OC.
(1)如图1,∠AOC=90°,∠BOC=120°,将△BOC绕点C顺时针旋转60°得到△ADC.点D恰好落在BO所在的直线上,用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)如图2,设∠AOC=α,∠BOC=β.当α= 120 °,β= 120 °时,OA+OB+OC有最小值.
【解答】解:(1)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△ADC≌△BOC,∠OCD=60°.
∴CD=OC,∠ADC=∠BOC=120°,AD=OB.
∴△OCD是等边三角形,
∴OC=OD=CD,∠COD=∠CDO=60°,
∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°,
∴∠AOD=30°,∠ADO=60°.
∴∠DAO=90°.
在Rt△ADO中,∠DAO=90°,
∴OA2+AD2=OD2.
∴OA2+OB2=OC2.
(2)如图2,当α=β=120°时,OA+OB+OC有最小值.理由如下:
作图如图2,
将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′.
∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°.
∴O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC.
∴△OC O′是等边三角形.
∴OC=O′C=OO′,∠COO′=∠CO′O=60°.
∵∠AOB=∠BOC=120°,
∴∠AOC=∠A′O′C=∠BOC=120°.
∴四点B,O,O′,A′共线.
∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小.
∴当α=β=120°时,OA+OB+OC有最小值,
故答案为:120,120.
25.(2024秋 宝山区校级期中)如图,抛物线y=﹣x2+mx+3(m>0)与x轴交于A、B两点(A在B左侧),与y轴交于点C.联结CB交对称轴于点E,点D为抛物线的顶点.
(1)联结AC、CD,若∠CED=45°
①求抛物线解析式;
②线段BC上一点F,∠ACB=∠FAB,联结FD,求tan∠FDE.
(2)平移抛物线,使新抛物线顶点D′在射线CD上,新抛物线与y轴交于点C′.若C′D平分∠CDE,且CD′=2CC′,求新抛物线的解析式.
【解答】解:(1)①令x=0,则 y=3,
∴C(0,3),
∴OC=3.
∵DE∥y轴,
∴∠OCB=∠CED=45°,
又∵∠BOC=90°,
∴OB=OC=3,
∴点B(3,0),
把点B(3,0)代入 y=﹣x2+mx+3(m>0)中,
得:﹣9+3m+3=0,
∴m=2,
∴抛物线的解析式为:y=﹣x2+2x+3.
②令y=0,则﹣x2+2x+3=0,解得:x1=﹣1,x2=3,
∵点A(﹣1,0),B(3,0),
∴AB=4.
如图1所示,
在 Rt△BOC 中,.
∵∠FAB=∠ACB,∠ABF=∠CBA,
∴△BAF∽△BCA,
∴,
则 .
过点F作FN⊥AB于点N,则△FNB 为等腰直角三角形,
∴,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),对称轴为直线 x=1,
∴FM=BN﹣2=﹣2=,
如图1,作FM垂直于直线 x=1于点M,
∴,
∴.
(2)如图2所示,
∵C′D平分∠CDE,
∴∠CDC′=∠C′DE,
∵DE∥y轴,
∴∠CC'D=∠C'DE=∠CDC',
∴CC′=CD,
又∵CD'=2CC'=2CD,
∴D为 CD'的中点,
对抛物线配方得:,
可得其顶点坐标为:,
设 D'(xD,yD'),因为C(0,3),由中点坐标公式得:
,,
故 .
∴新抛物线解析式为:
,
令x=0,则 ,则 ,
又CD=CC',根据两点间距离公式有:
CD2=CC'2,
即 =,
∴,
∵m>0,m2>0,
∴4m2=4+m2,解得:,
∴新抛物线解析式为:
.
26.(2024秋 琼山区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和C(3,0),与y轴交于点B(0,3),P是抛物线上的一动点.
(1)求抛物线的表达式;
(2)若点D(2,3)向下平移8个单位长度,向右平移m(m>0)个单位长度后,恰好落在y=﹣x2+bx+c的图象上,求m的值;
(3)连接BC,当∠CAP=∠ACB时,求点P的坐标.
【解答】解:(1)由题意得:
y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)由题意得,点D(2,3)平移后点的横坐标为D′(2+m,3﹣8),
∵D′(2+m,3﹣8)恰好落在y=﹣(x+1)(x﹣3)的图象上,
∴﹣(2+m+1)(2+m﹣3)=﹣5,
整理得:m2+2m﹣8=0,
解得:m=2或m=﹣4(舍去),
∴m的值为2;
(3)过点A作AD∥BC交y轴于点D,连接AD交抛物线于点P,如图1,则∠CAP=∠ACB,
∵点A(﹣1,0),点B(0,3),
∴OC=OB=3,
∴∠OCB=∠OBC=45°,
∴∠OAD=∠ODA=45°,
∵点A(﹣1,0),
∴OA=OD=1,
∴点D(0,﹣1),
设直线AD的解析式为y=kx﹣1,将点A,点D的坐标代入得:
0=﹣k﹣1,
解得:k=﹣1,
∴直线AD的解析式为y=﹣x﹣1,
联立得,
解得:或(与点A重合,舍去),
∴点P的坐标为(4,﹣5);
作点D关于原点的对称点D′,连接AD′交抛物线于点P,如图2,则∠CAD′=∠ACB,
则D′(0,1),同理求得直线AD′的解析式为y=x+1,
联立得,
解得:或(与点A重合,舍去),
∴点P的坐标为(2,3);
综上,点P的坐标为(2,3)或(4,﹣5).
一.选择题(共9小题)
1.(2024秋 临潼区期中)下列字母既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(2024秋 崂山区期中)若一元二次方程3x2=5x+2的二次项系数是3,则它的常数项是( )
A.﹣2 B.2 C.﹣5 D.5
3.(2024秋 新会区校级月考)方程(x+1)(x﹣1)=0的根是( )
A.x1=x2=1 B.x1=1,x2=﹣1
C.x1=x2=﹣1 D.x1=1,x2=0
4.(2024秋 青山区期中)有一个人患了流感,经过两轮传染后,共有81个人患了流感,设平均每轮每人传染x个人,则下列等式成立的是( )
A.1+x+x2=81 B.1+x+x(x+1)=81
C.1+x+(1+x)2=81 D.1+(1+x)2=81
5.(2024秋 大兴区期中)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,则∠B1度数为( )
A.29° B.32° C.58° D.61°
6.(2024秋 铁西区校级月考)如图,直线a∥b,△AOB的边OB在直线b上,∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1为( )
A.50° B.55° C.60° D.75°
7.(2024秋 信阳期中)关于x的二次函数y=(a+1)x2+ax+2a2﹣2的图象过原点,则a的值为( )
A.﹣1 B.1 C.±1 D.0
8.(2024秋 开鲁县校级期中)关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下
B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小
D.图象的顶点坐标为(﹣3,﹣2)
9.(2024秋 南开区期中)二次函数y=ax2+bx+c(a≠0)的图象开口向下,与x轴交于点(﹣3,0),其对称轴为直线,有下列结论:①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④对于任意非零实数m,若x1,x2(x1<x2)为方程a(x+3)(x﹣2)+m2=0的两个根,则x1<﹣3且x2>2.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共9小题)
10.(2024秋 朝阳区校级期中)若m、n是一元二次方程3x2﹣kx+2=0的两个根,则mn= .
11.(2024秋 大兴区期中)在平面直角坐标系xOy中,点(﹣2,3)关于原点的对称点坐标为 .
12.(2024秋 蓬江区校级期中)将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若AB=2,将三角板绕原点O逆时针旋转60°,则点A的对应点A′的坐标为 .
13.(2024秋 南开区期中)如图,Rt△ABC中,AB=8,BC=2,∠BCA=90°,将Rt△ABC绕着点A顺时针旋转,得到Rt△AB′C′,点B,C的对应点分别为B′,C′,连接CC′,交AB于点M,点M恰为AB边中点.
(Ⅰ)△AMC的面积为 ;
(Ⅱ)线段C′M的长为 .
14.(2024秋 建邺区期中)若关于x的方程x2﹣6x+m+1=0有两个不相等的实数根,则m的取值范围是 .
15.(2024秋 大兴区期中)某校生物学科老师在组织学生进行野外实践活动时,学生发现自然界的植物生长具有神奇的规律.比如某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,设这种植物每个支干长出的小分支个数为x,则可列方程为 .
16.(2024秋 大兴区期中)已知抛物线y=x2﹣4x+c与x轴没有交点,则实数c的取值范围是 .
17.(2024秋 崂山区期中)在正常情况下,10米跳台跳水运动员必须在距水面不小于5m时完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员距离水面的高度h(m)和运动员起跳后的运动时间t(s)之间满足关系:h=10+2.5t﹣5t2,则当h=5时,10+2.5t﹣5t2=5即2t2﹣t﹣2=0.
t 1.1 1.2 1.3 1.4
2t2﹣t﹣2 ﹣0.68 ﹣0.32 0.08 0.52
根据表格中的对应值,可判断运动员完成动作的时间最多不超过 s.(精确到0.1)
18.(2024秋 信阳期中)定义:由a,b构造的二次函数y=ax2+(a﹣b)x﹣b叫作一次函数y=ax﹣b的“滋生函数”,一次函数y=ax﹣b叫作二次函数y=ax2+(a﹣b)x﹣b的“本源函数”(a,b为常数,且a≠0).若一次函数y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,则二次函数y=ax2﹣4x+a+2的“本源函数”是 .
三.解答题(共8小题)
19.(2024秋 昂仁县期中)解方程:
(1)x2﹣4x+3=0;
(2)1﹣8x+16x2=2﹣8x;
(3)(x﹣2)2+x(x﹣2)=0.
20.(2024秋 建邺区期中)关于x的一元二次方程mx2+nx+2=0.
(1)求证:当n=m+2时,此方程必有实数根;
(2)若方程有两个相等的整数根,写出满足条件的一组m,n的值,并求此时方程的根.
21.(2024秋 浦北县期中)如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的三个顶点均在格点上.
(1)将△ABC向x轴正方向平移5个单位长度得到△A1B1C1,画出△A1B1C1;
(2)在(1)的条件下,以点O为中心,将△A1B1C1旋转180°得△A2B2C2,画出△A2B2C2.
22.(2024秋 崂山区期中)面向日益严峻的气候变化形势,以发展新能源汽车推动道路交通领域零碳转型已成为全球共识.我国政府不断加大对新能源汽车的支持和推动,新能源汽车的市场需求正在不断增加.如表是一款某品牌新能源热门车型7月份和9月份的全国销量情况:
月份 7月 9月
销量/万辆 2.5 3.6
(1)求该款车销量的月平均增长率.
(2)青岛一个该品牌4S店购进一批该款车型进行销售,已知进价为每辆6万元.经试销发现:当该款汽车售价为7.5万元时,平均每月销量为150辆;而当售价每降低0.1万元时,平均每月就能多售出15辆.为了扩大销量,该4S店决定降价促销,若该4S店想要维持利润不变,该款车的售价应为每辆多少万元?
23.(2024秋 安定区期中)已知抛物线y=x2+bx+c过(0,8),(6,8)两点.
(1)求出该抛物线的解析式;
(2)求出抛物线与x轴的交点坐标;
(3)当y<0时,写出x的取值范围.
24.(2024秋 大兴区期中)已知,△ABC是等腰三角形,∠BAC=60°,O是△ABC内的任意一点,连接OA,OB,OC.
(1)如图1,∠AOC=90°,∠BOC=120°,将△BOC绕点C顺时针旋转60°得到△ADC.点D恰好落在BO所在的直线上,用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)如图2,设∠AOC=α,∠BOC=β.当α= °,β= °时,OA+OB+OC有最小值.
25.(2024秋 宝山区校级期中)如图,抛物线y=﹣x2+mx+3(m>0)与x轴交于A、B两点(A在B左侧),与y轴交于点C.联结CB交对称轴于点E,点D为抛物线的顶点.
(1)联结AC、CD,若∠CED=45°
①求抛物线解析式;
②线段BC上一点F,∠ACB=∠FAB,联结FD,求tan∠FDE.
(2)平移抛物线,使新抛物线顶点D′在射线CD上,新抛物线与y轴交于点C′.若C′D平分∠CDE,且CD′=2CC′,求新抛物线的解析式.
26.(2024秋 琼山区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和C(3,0),与y轴交于点B(0,3),P是抛物线上的一动点.
(1)求抛物线的表达式;
(2)若点D(2,3)向下平移8个单位长度,向右平移m(m>0)个单位长度后,恰好落在y=﹣x2+bx+c的图象上,求m的值;
(3)连接BC,当∠CAP=∠ACB时,求点P的坐标.
第21-23章复习卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
一.选择题(共9小题)
1.(2024秋 临潼区期中)下列字母既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解答】解:A.“H”既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.“S”不是轴对称图形,是中心对称图形,故本选项不符合题意;
C.“A”是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.“Q”既不是轴对称图形,也不是中心对称图形,故本选项不符合题意.
故选:A.
2.(2024秋 崂山区期中)若一元二次方程3x2=5x+2的二次项系数是3,则它的常数项是( )
A.﹣2 B.2 C.﹣5 D.5
【解答】解:方程3x2=5x+2,
整理得:3x2﹣5x﹣2=0,
则常数项是﹣2.
故选:A.
3.(2024秋 新会区校级月考)方程(x+1)(x﹣1)=0的根是( )
A.x1=x2=1 B.x1=1,x2=﹣1
C.x1=x2=﹣1 D.x1=1,x2=0
【解答】解:∵(x+1)(x﹣1)=0,
∴x﹣1=0或x+1=0,
解得x1=1,x2=﹣1,
故选:B.
4.(2024秋 青山区期中)有一个人患了流感,经过两轮传染后,共有81个人患了流感,设平均每轮每人传染x个人,则下列等式成立的是( )
A.1+x+x2=81 B.1+x+x(x+1)=81
C.1+x+(1+x)2=81 D.1+(1+x)2=81
【解答】解:依题意得1+x+x(x+1)=81.
故选:B.
5.(2024秋 大兴区期中)如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,则∠B1度数为( )
A.29° B.32° C.58° D.61°
【解答】解:∵将△ABC绕点C逆时针方向旋转58°得到△A1B1C.若点A1恰好落在AB边上,
∴AC=A1C,∠ACA1=58°,∠B=∠B1,
∴∠A=∠AA1C=(180°﹣58°)=61°,
∵∠ACB=90°,
∴∠B=90°﹣61°=29°,
∴∠B1=∠B=29°,
故选:A.
6.(2024秋 铁西区校级月考)如图,直线a∥b,△AOB的边OB在直线b上,∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1为( )
A.50° B.55° C.60° D.75°
【解答】解:如图:
由题意可得:∠A1OB1=∠AOB=55°,∠AOA1=75°,
∴∠A1OD=180°﹣55°﹣75°=50°,
∵直线a∥b,
∴∠1=∠A1OD=50°,
故选:A.
7.(2024秋 信阳期中)关于x的二次函数y=(a+1)x2+ax+2a2﹣2的图象过原点,则a的值为( )
A.﹣1 B.1 C.±1 D.0
【解答】解:把(0,0)代入y=(a+1)x2+3x+a2﹣1得a2﹣1=0,
解得a=1或a=﹣1,
而a+1≠0,
所以a的值为1.
故选:B.
8.(2024秋 开鲁县校级期中)关于二次函数的图象与性质,下列结论错误的是( )
A.图象开口向下
B.当x=3时,y有最大值﹣2
C.当x>3时,y随x的增大而减小
D.图象的顶点坐标为(﹣3,﹣2)
【解答】解:∵二次函数,a=<0,
∴开口向下,顶点坐标为(3,﹣2);当x=3时,y有最大值﹣2;当x>3时,y随x的增大而减小;图象的顶点坐标为(3,﹣2);
∴D选项错误,符合题意,
故选:D.
9.(2024秋 南开区期中)二次函数y=ax2+bx+c(a≠0)的图象开口向下,与x轴交于点(﹣3,0),其对称轴为直线,有下列结论:①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④对于任意非零实数m,若x1,x2(x1<x2)为方程a(x+3)(x﹣2)+m2=0的两个根,则x1<﹣3且x2>2.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线与x轴交于点(﹣3,0),对称轴为直线,
∴抛物线与x轴的另一个交点为(2,0),
∴抛物线与y轴交于正半轴,
∴c>0,
∵﹣=﹣,
∴a=b,
∴abc>0,故①正确;
∵抛物线解析式为y=ax2+ax+c经过(﹣3,0),
∴9a﹣3a+c=0,
∴6a+c=0,
∴3a+3a+c=0,
∵3a<0,
∴3a+c>0,故②正确;
∵当x>﹣时,y随x的增大而减小,故③错误;
由题意x1,x2(x1<x2)是抛物线y=a(x+3)(x﹣2)与直线y=﹣m2交点的横坐标,
∴x1<﹣3,x2>2,故④正确.
故选:C.
二.填空题(共9小题)
10.(2024秋 朝阳区校级期中)若m、n是一元二次方程3x2﹣kx+2=0的两个根,则mn= .
【解答】解:∵m、n是一元二次方程3x2﹣kx+2=0的根,
∴mn=.
故答案为:.
11.(2024秋 大兴区期中)在平面直角坐标系xOy中,点(﹣2,3)关于原点的对称点坐标为 (2,﹣3) .
【解答】解:点(﹣2,3)关于原点O对称的点的坐标是:(2,﹣3).
故答案为:(2,﹣3).
12.(2024秋 蓬江区校级期中)将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若AB=2,将三角板绕原点O逆时针旋转60°,则点A的对应点A′的坐标为 (0) .
【解答】解:由题意得,将三角板绕原点O逆时针旋转60°,点A的对应点A′落在y轴的正半轴上.
在Rt△AOB中,∠AOB=30°,AB=2,
∴OA===,
∴OA'=OA=,
∴点A′的坐标为(0).
故答案为:(0).
13.(2024秋 南开区期中)如图,Rt△ABC中,AB=8,BC=2,∠BCA=90°,将Rt△ABC绕着点A顺时针旋转,得到Rt△AB′C′,点B,C的对应点分别为B′,C′,连接CC′,交AB于点M,点M恰为AB边中点.
(Ⅰ)△AMC的面积为 ;
(Ⅱ)线段C′M的长为 11 .
【解答】解:(1)∵AB=8,BC=2,∠BCA=90°,
∴AC===,
∴S△ABC===.
∵点M为AB边中点,
∴=.
故答案为:.
(2)过点A作AD⊥CC'于点D,
由旋转得,AC=AC',
∴△ACC'为等腰三角形,
∴CD=C'D.
∵点M为AB边中点,∠BCA=90°,
∴CM==AM=4,
∴∠ACM=∠CAM.
∵cos∠CAB==,
∴cos∠ACM==,
∴CD=,
∴CC'=2CD=15,
∴C'M=CC'﹣CM=15﹣4=11.
故答案为:11.
14.(2024秋 建邺区期中)若关于x的方程x2﹣6x+m+1=0有两个不相等的实数根,则m的取值范围是 m<8 .
【解答】解:根据题意得Δ=(﹣6)2﹣4×1×(m+1)>0,
解得m<8.
故答案为:m<8.
15.(2024秋 大兴区期中)某校生物学科老师在组织学生进行野外实践活动时,学生发现自然界的植物生长具有神奇的规律.比如某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,设这种植物每个支干长出的小分支个数为x,则可列方程为 x2+x+1=43 .
【解答】解:根据题意列方程得:x2+x+1=43.
故答案为:x2+x+1=43.
16.(2024秋 大兴区期中)已知抛物线y=x2﹣4x+c与x轴没有交点,则实数c的取值范围是 c>4 .
【解答】解:若抛物线y=x2﹣4x+c与x轴没有交点,则Δ=(﹣4)2﹣4c<0,
解得c>4.
故答案为:c>4.
17.(2024秋 崂山区期中)在正常情况下,10米跳台跳水运动员必须在距水面不小于5m时完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员距离水面的高度h(m)和运动员起跳后的运动时间t(s)之间满足关系:h=10+2.5t﹣5t2,则当h=5时,10+2.5t﹣5t2=5即2t2﹣t﹣2=0.
t 1.1 1.2 1.3 1.4
2t2﹣t﹣2 ﹣0.68 ﹣0.32 0.08 0.52
根据表格中的对应值,可判断运动员完成动作的时间最多不超过 1.3 s.(精确到0.1)
【解答】解:根据表格中的对应值,可判断运动员完成动作的时间最多不超过1.3s,
故答案为:1.3.
18.(2024秋 信阳期中)定义:由a,b构造的二次函数y=ax2+(a﹣b)x﹣b叫作一次函数y=ax﹣b的“滋生函数”,一次函数y=ax﹣b叫作二次函数y=ax2+(a﹣b)x﹣b的“本源函数”(a,b为常数,且a≠0).若一次函数y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,则二次函数y=ax2﹣4x+a+2的“本源函数”是 y=﹣3x﹣1 .
【解答】解:∵y=ax﹣b的“滋生函数”是y=ax2﹣4x+a+2,
∴y=ax2﹣4x+a+2=ax2+(a﹣b)x﹣b,即,
解得,
∴y=ax2﹣4x+a+2的“本源函数”是y=﹣3x﹣1,
故答案为:y=﹣3x﹣1.
三.解答题(共8小题)
19.(2024秋 昂仁县期中)解方程:
(1)x2﹣4x+3=0;
(2)1﹣8x+16x2=2﹣8x;
(3)(x﹣2)2+x(x﹣2)=0.
【解答】解:(1)∵x2﹣4x+3=0,
∴(x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
解得x1=1,x2=3;
(2)1﹣8x+16x2=2﹣8x,
移项及合并同类项,得:16x2=1,
系数化为1,得:,
∴;
(3)∵(x﹣2)2+x(x﹣2)=0,
∴(x﹣2)(x﹣2+x)=0,
∴x﹣2=0或x﹣2+x=0,
解得x1=2,x2=1.
20.(2024秋 建邺区期中)关于x的一元二次方程mx2+nx+2=0.
(1)求证:当n=m+2时,此方程必有实数根;
(2)若方程有两个相等的整数根,写出满足条件的一组m,n的值,并求此时方程的根.
【解答】解:(1)∵Δ=n2﹣8m,
当n=m+2时,Δ=(m+2)2﹣8m=(m﹣2)2≥0,
∴方程必有实数根;
(2)∵方程有两个相等的整数根,
∴Δ=n2﹣8m=0,
若n=4,m=2,
则方程变形为2x2+4x+2=0,
解得x1=x2=﹣1.
21.(2024秋 浦北县期中)如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的三个顶点均在格点上.
(1)将△ABC向x轴正方向平移5个单位长度得到△A1B1C1,画出△A1B1C1;
(2)在(1)的条件下,以点O为中心,将△A1B1C1旋转180°得△A2B2C2,画出△A2B2C2.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
22.(2024秋 崂山区期中)面向日益严峻的气候变化形势,以发展新能源汽车推动道路交通领域零碳转型已成为全球共识.我国政府不断加大对新能源汽车的支持和推动,新能源汽车的市场需求正在不断增加.如表是一款某品牌新能源热门车型7月份和9月份的全国销量情况:
月份 7月 9月
销量/万辆 2.5 3.6
(1)求该款车销量的月平均增长率.
(2)青岛一个该品牌4S店购进一批该款车型进行销售,已知进价为每辆6万元.经试销发现:当该款汽车售价为7.5万元时,平均每月销量为150辆;而当售价每降低0.1万元时,平均每月就能多售出15辆.为了扩大销量,该4S店决定降价促销,若该4S店想要维持利润不变,该款车的售价应为每辆多少万元?
【解答】解:(1)设该款车销量的月平均增长率为x,
根据题意得:2.5(1+x)2=3.6,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:该款车销量的月平均增长率为20%;
(2)设该款车的售价为每辆y万元,则每辆的销售利润为(y﹣6)万元,平均每月可售出150+×15=(1275﹣150y)辆,
根据题意得:(y﹣6)(1275﹣150y)=(7.5﹣6)×150,
整理得:2y2﹣29y+105=0,
解得:y1=7,y2=7.5(不符合题意,舍去).
答:该款车的售价应为每辆7万元.
23.(2024秋 安定区期中)已知抛物线y=x2+bx+c过(0,8),(6,8)两点.
(1)求出该抛物线的解析式;
(2)求出抛物线与x轴的交点坐标;
(3)当y<0时,写出x的取值范围.
【解答】解:(1)∵抛物线y=x2+bx+c过(0,8),(6,8)两点,
∴
解得:
∴该抛物线的解析式为y=x2﹣6x+8;
(2)将y=0代入y=x2﹣6x+8,得x2﹣6x+8=0
解得:x1=2,x2=4
∴抛物线与x轴的交点坐标为(2,0)和(4,0);
(3)∵y=x2+bx+c中,a=1>0,其图象大致如下
由图象可知:当y<0时,2<x<4.
24.(2024秋 大兴区期中)已知,△ABC是等腰三角形,∠BAC=60°,O是△ABC内的任意一点,连接OA,OB,OC.
(1)如图1,∠AOC=90°,∠BOC=120°,将△BOC绕点C顺时针旋转60°得到△ADC.点D恰好落在BO所在的直线上,用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)如图2,设∠AOC=α,∠BOC=β.当α= 120 °,β= 120 °时,OA+OB+OC有最小值.
【解答】解:(1)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△ADC≌△BOC,∠OCD=60°.
∴CD=OC,∠ADC=∠BOC=120°,AD=OB.
∴△OCD是等边三角形,
∴OC=OD=CD,∠COD=∠CDO=60°,
∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°,
∴∠AOD=30°,∠ADO=60°.
∴∠DAO=90°.
在Rt△ADO中,∠DAO=90°,
∴OA2+AD2=OD2.
∴OA2+OB2=OC2.
(2)如图2,当α=β=120°时,OA+OB+OC有最小值.理由如下:
作图如图2,
将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′.
∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°.
∴O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC.
∴△OC O′是等边三角形.
∴OC=O′C=OO′,∠COO′=∠CO′O=60°.
∵∠AOB=∠BOC=120°,
∴∠AOC=∠A′O′C=∠BOC=120°.
∴四点B,O,O′,A′共线.
∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小.
∴当α=β=120°时,OA+OB+OC有最小值,
故答案为:120,120.
25.(2024秋 宝山区校级期中)如图,抛物线y=﹣x2+mx+3(m>0)与x轴交于A、B两点(A在B左侧),与y轴交于点C.联结CB交对称轴于点E,点D为抛物线的顶点.
(1)联结AC、CD,若∠CED=45°
①求抛物线解析式;
②线段BC上一点F,∠ACB=∠FAB,联结FD,求tan∠FDE.
(2)平移抛物线,使新抛物线顶点D′在射线CD上,新抛物线与y轴交于点C′.若C′D平分∠CDE,且CD′=2CC′,求新抛物线的解析式.
【解答】解:(1)①令x=0,则 y=3,
∴C(0,3),
∴OC=3.
∵DE∥y轴,
∴∠OCB=∠CED=45°,
又∵∠BOC=90°,
∴OB=OC=3,
∴点B(3,0),
把点B(3,0)代入 y=﹣x2+mx+3(m>0)中,
得:﹣9+3m+3=0,
∴m=2,
∴抛物线的解析式为:y=﹣x2+2x+3.
②令y=0,则﹣x2+2x+3=0,解得:x1=﹣1,x2=3,
∵点A(﹣1,0),B(3,0),
∴AB=4.
如图1所示,
在 Rt△BOC 中,.
∵∠FAB=∠ACB,∠ABF=∠CBA,
∴△BAF∽△BCA,
∴,
则 .
过点F作FN⊥AB于点N,则△FNB 为等腰直角三角形,
∴,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),对称轴为直线 x=1,
∴FM=BN﹣2=﹣2=,
如图1,作FM垂直于直线 x=1于点M,
∴,
∴.
(2)如图2所示,
∵C′D平分∠CDE,
∴∠CDC′=∠C′DE,
∵DE∥y轴,
∴∠CC'D=∠C'DE=∠CDC',
∴CC′=CD,
又∵CD'=2CC'=2CD,
∴D为 CD'的中点,
对抛物线配方得:,
可得其顶点坐标为:,
设 D'(xD,yD'),因为C(0,3),由中点坐标公式得:
,,
故 .
∴新抛物线解析式为:
,
令x=0,则 ,则 ,
又CD=CC',根据两点间距离公式有:
CD2=CC'2,
即 =,
∴,
∵m>0,m2>0,
∴4m2=4+m2,解得:,
∴新抛物线解析式为:
.
26.(2024秋 琼山区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和C(3,0),与y轴交于点B(0,3),P是抛物线上的一动点.
(1)求抛物线的表达式;
(2)若点D(2,3)向下平移8个单位长度,向右平移m(m>0)个单位长度后,恰好落在y=﹣x2+bx+c的图象上,求m的值;
(3)连接BC,当∠CAP=∠ACB时,求点P的坐标.
【解答】解:(1)由题意得:
y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)由题意得,点D(2,3)平移后点的横坐标为D′(2+m,3﹣8),
∵D′(2+m,3﹣8)恰好落在y=﹣(x+1)(x﹣3)的图象上,
∴﹣(2+m+1)(2+m﹣3)=﹣5,
整理得:m2+2m﹣8=0,
解得:m=2或m=﹣4(舍去),
∴m的值为2;
(3)过点A作AD∥BC交y轴于点D,连接AD交抛物线于点P,如图1,则∠CAP=∠ACB,
∵点A(﹣1,0),点B(0,3),
∴OC=OB=3,
∴∠OCB=∠OBC=45°,
∴∠OAD=∠ODA=45°,
∵点A(﹣1,0),
∴OA=OD=1,
∴点D(0,﹣1),
设直线AD的解析式为y=kx﹣1,将点A,点D的坐标代入得:
0=﹣k﹣1,
解得:k=﹣1,
∴直线AD的解析式为y=﹣x﹣1,
联立得,
解得:或(与点A重合,舍去),
∴点P的坐标为(4,﹣5);
作点D关于原点的对称点D′,连接AD′交抛物线于点P,如图2,则∠CAD′=∠ACB,
则D′(0,1),同理求得直线AD′的解析式为y=x+1,
联立得,
解得:或(与点A重合,舍去),
∴点P的坐标为(2,3);
综上,点P的坐标为(2,3)或(4,﹣5).
同课章节目录
