华师大版八年级数学上册课件:13.2 三角形全等的判定(SAS)(共20张PPT)
文档属性
| 名称 | 华师大版八年级数学上册课件:13.2 三角形全等的判定(SAS)(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-14 00:00:00 | ||
图片预览


文档简介
课件20张PPT。-SAS13.2 三角形全等的判定方法两个条件
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。即一组或两组条件对应相等的两个三角形不能判定全等。一个条件
①一角;
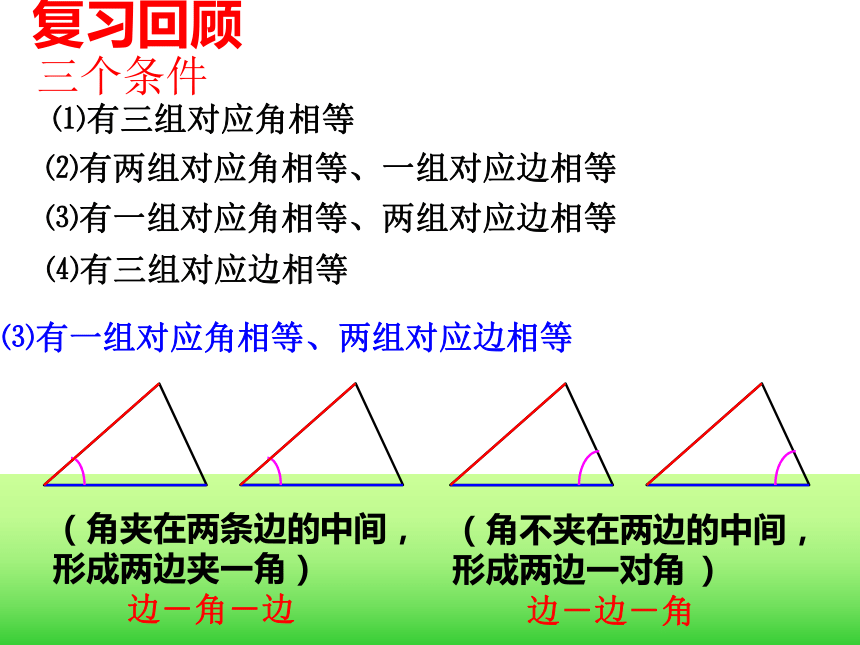
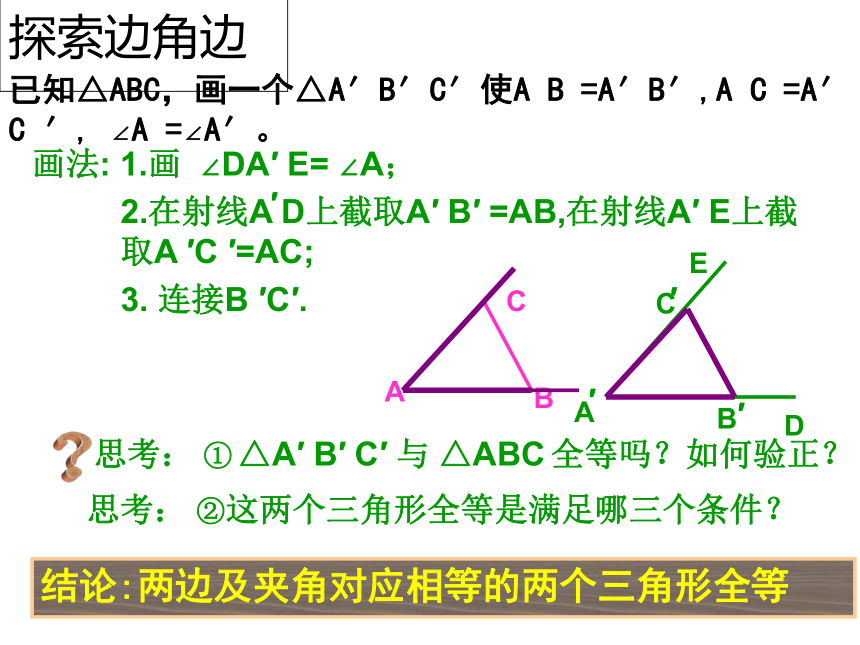
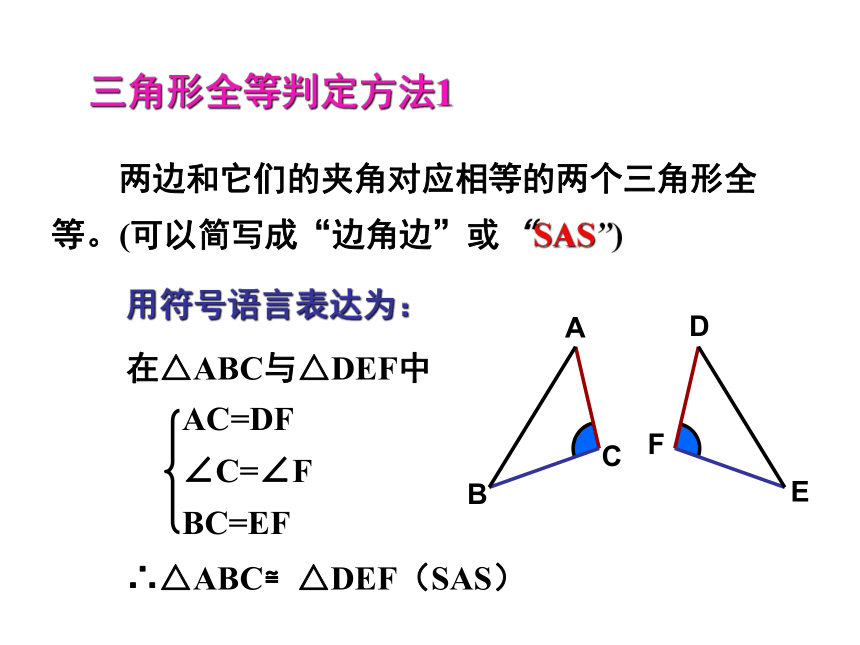
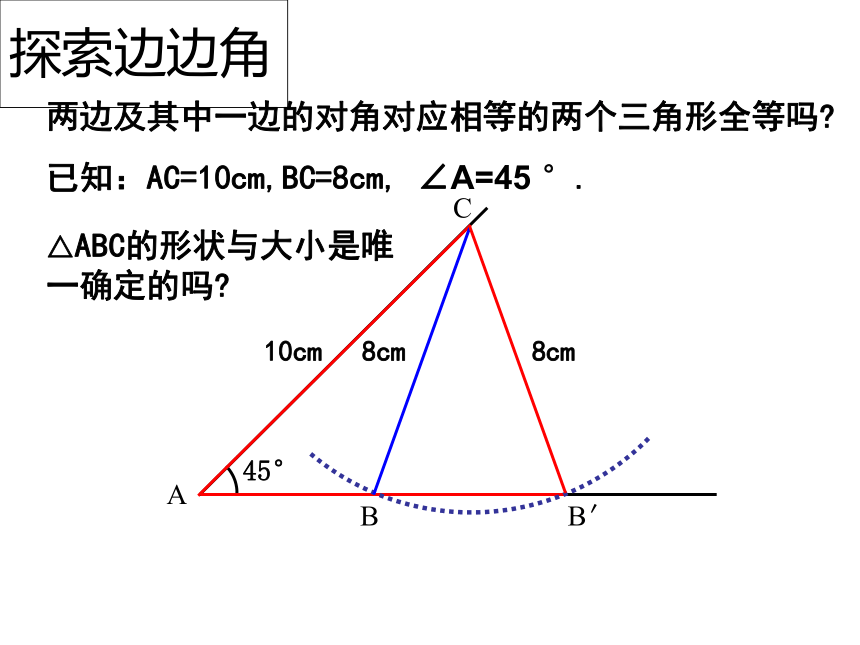
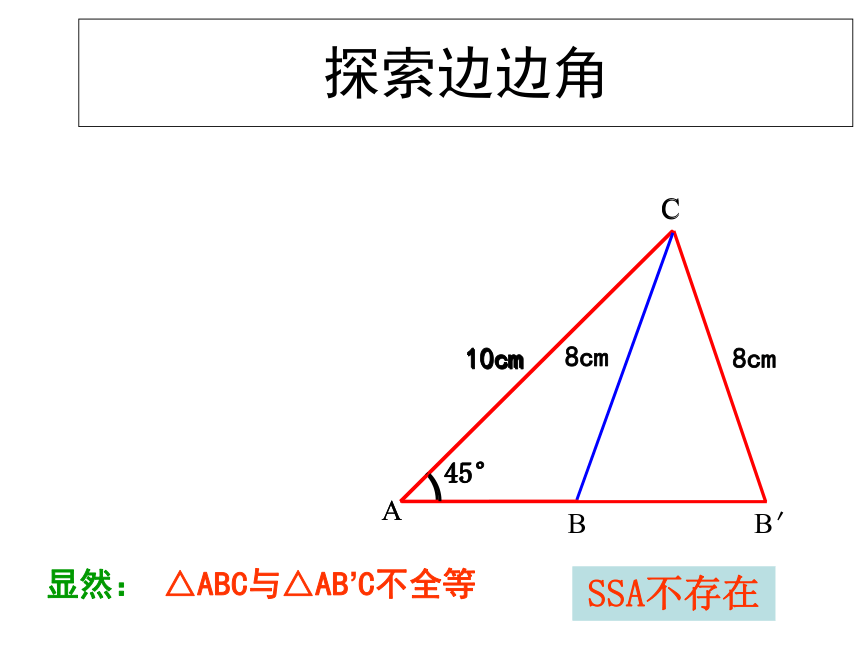
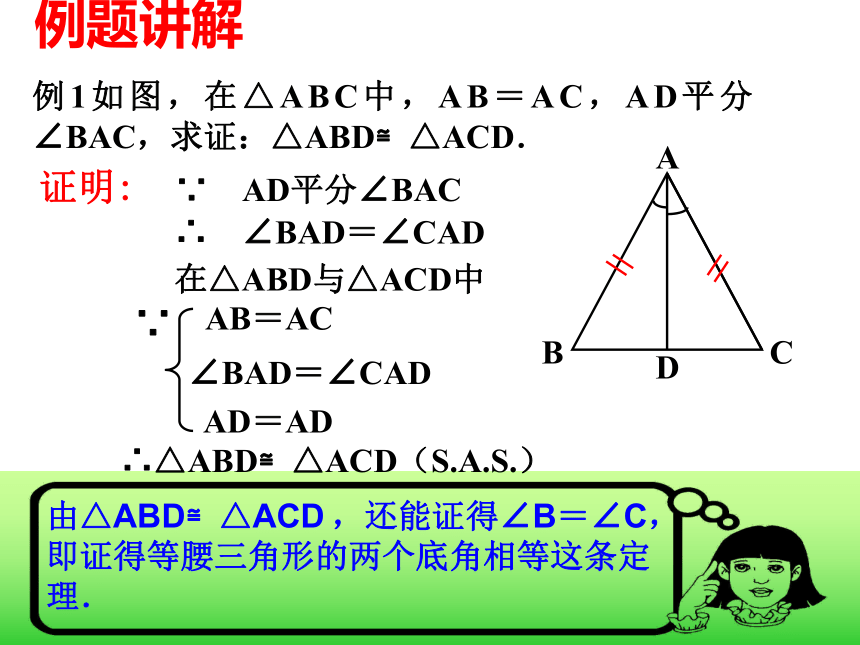
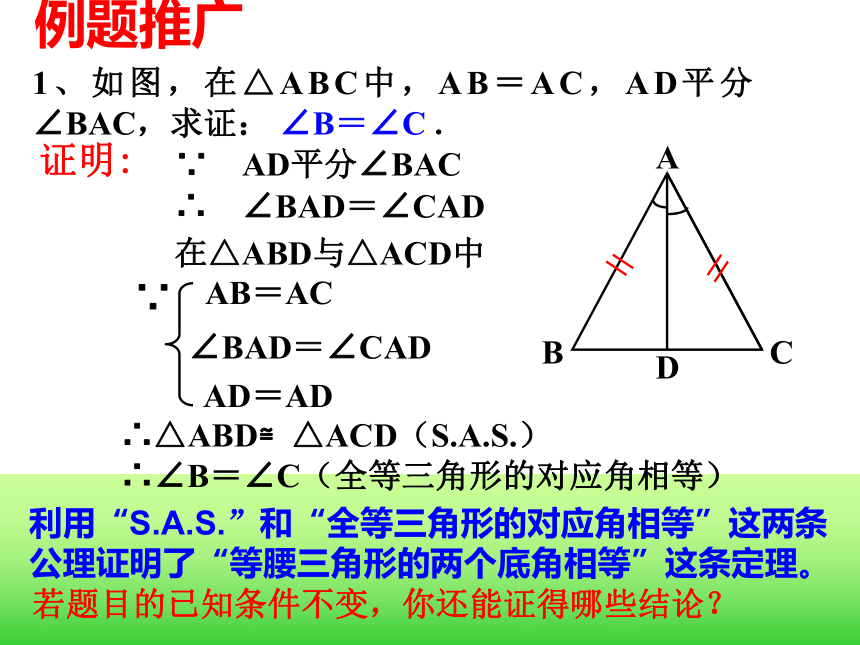
②一边;复习回顾探索三角形全等的条件⑴有三组对应角相等 ⑵有两组对应角相等、一组对应边相等 ⑶有一组对应角相等、两组对应边相等 ⑷有三组对应边相等 复习回顾⑶有一组对应角相等、两组对应边相等 边-角-边边-边-角(角夹在两条边的中间,形成两边夹一角) (角不夹在两边的中间,形成两边一对角 ) 三个条件 已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。结论:两边及夹角对应相等的两个三角形全等?思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正?画法: 1.画 ∠DA′ E= ∠A;2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;3. 连接B ′C′.′ACBA′EDCB′′思考: ②这两个三角形全等是满足哪三个条件?探索边角边 三角形全等判定方法1用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA探索边边角两边及其中一边的对角对应相等的两个三角形全等吗?已知:AC=10cm,BC=8cm, ∠A=45 °.△ABC的形状与大小是唯一确定的吗?探索边边角SSA不存在显然: △ABC与△AB’C不全等例题讲解例1如图,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.证明: ∴ ∠BAD=∠CAD AD=AD∴△ABD≌△ACD(S.A.S.)∵ AD平分∠BAC在△ABD与△ACD中∵AB=AC∠BAD=∠CAD由△ABD≌△ACD ,还能证得∠B=∠C,即证得等腰三角形的两个底角相等这条定理.例题推广1、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: ∠B=∠C .证明: ∴∠B=∠C(全等三角形的对应角相等)利用“S.A.S.”和“全等三角形的对应角相等”这两条公理证明了“等腰三角形的两个底角相等”这条定理。若题目的已知条件不变,你还能证得哪些结论?例题推广2、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: .BD=CD,证明: ∴BD=CD(全等三角形的对应边相等)AD⊥BC ∴ ∠ADB= ∠ADC (全等三角形的对应角相等)
又∵ ∠ADB+ ∠ADC=180°
∴ ∠ADB= ∠ADC= 90°∴ AD⊥BC“三线合一”这说明了什么?等腰三角形顶角的平分线,就是底边上的中线,也是底边上的高。1、根据题目条件,判断下面的三角形是否全等.
(1) AC=DF,∠C=∠F,BC=EF;
(2) BC=BD,∠ABC=∠ABD.
(1)全等(2)全等巩固训练C2.在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS巩固训练(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中巩固训练3.已知AB∥DC, AD=BC , ∠A=∠B,点M是AB的中点,求证: △AMD≌△BMC .证明:
∵点M是AB的中点,
∴ AM=BM。
在△ADM和△BCM中AD=BC
∠A=∠B
AM=BM ∴△AMD≌△BMC (S.A.S.)巩固训练∵1.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●●●展示提升2如图,已知:AB=AD,AC=AE,∠1=∠2,
求证:∠B=∠D.
展示提升3.如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,
求证:AB=AD.
展示提升课堂小结今天你学到了什么?1、今天我们学习了哪种方法判定两个三角形全等?通过证明三角形全等可以证明两条线段相等等、两个角相等。答:S.A.S.(边角边)(角夹在两条边的中间,形成两边夹一角) 2、 “边边角”能不能判定两个三角形全等?答:不能再见!
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。即一组或两组条件对应相等的两个三角形不能判定全等。一个条件
①一角;
②一边;复习回顾探索三角形全等的条件⑴有三组对应角相等 ⑵有两组对应角相等、一组对应边相等 ⑶有一组对应角相等、两组对应边相等 ⑷有三组对应边相等 复习回顾⑶有一组对应角相等、两组对应边相等 边-角-边边-边-角(角夹在两条边的中间,形成两边夹一角) (角不夹在两边的中间,形成两边一对角 ) 三个条件 已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。结论:两边及夹角对应相等的两个三角形全等?思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正?画法: 1.画 ∠DA′ E= ∠A;2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;3. 连接B ′C′.′ACBA′EDCB′′思考: ②这两个三角形全等是满足哪三个条件?探索边角边 三角形全等判定方法1用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA探索边边角两边及其中一边的对角对应相等的两个三角形全等吗?已知:AC=10cm,BC=8cm, ∠A=45 °.△ABC的形状与大小是唯一确定的吗?探索边边角SSA不存在显然: △ABC与△AB’C不全等例题讲解例1如图,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.证明: ∴ ∠BAD=∠CAD AD=AD∴△ABD≌△ACD(S.A.S.)∵ AD平分∠BAC在△ABD与△ACD中∵AB=AC∠BAD=∠CAD由△ABD≌△ACD ,还能证得∠B=∠C,即证得等腰三角形的两个底角相等这条定理.例题推广1、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: ∠B=∠C .证明: ∴∠B=∠C(全等三角形的对应角相等)利用“S.A.S.”和“全等三角形的对应角相等”这两条公理证明了“等腰三角形的两个底角相等”这条定理。若题目的已知条件不变,你还能证得哪些结论?例题推广2、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: .BD=CD,证明: ∴BD=CD(全等三角形的对应边相等)AD⊥BC ∴ ∠ADB= ∠ADC (全等三角形的对应角相等)
又∵ ∠ADB+ ∠ADC=180°
∴ ∠ADB= ∠ADC= 90°∴ AD⊥BC“三线合一”这说明了什么?等腰三角形顶角的平分线,就是底边上的中线,也是底边上的高。1、根据题目条件,判断下面的三角形是否全等.
(1) AC=DF,∠C=∠F,BC=EF;
(2) BC=BD,∠ABC=∠ABD.
(1)全等(2)全等巩固训练C2.在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS巩固训练(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中巩固训练3.已知AB∥DC, AD=BC , ∠A=∠B,点M是AB的中点,求证: △AMD≌△BMC .证明:
∵点M是AB的中点,
∴ AM=BM。
在△ADM和△BCM中AD=BC
∠A=∠B
AM=BM ∴△AMD≌△BMC (S.A.S.)巩固训练∵1.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●●●展示提升2如图,已知:AB=AD,AC=AE,∠1=∠2,
求证:∠B=∠D.
展示提升3.如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,
求证:AB=AD.
展示提升课堂小结今天你学到了什么?1、今天我们学习了哪种方法判定两个三角形全等?通过证明三角形全等可以证明两条线段相等等、两个角相等。答:S.A.S.(边角边)(角夹在两条边的中间,形成两边夹一角) 2、 “边边角”能不能判定两个三角形全等?答:不能再见!
