华师大版九年级数学上册课件:第22章 一元二次方程小结课件(共20张PPT)
文档属性
| 名称 | 华师大版九年级数学上册课件:第22章 一元二次方程小结课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-14 00:00:00 | ||
图片预览








文档简介
课件20张PPT。大声喊出我们的口号:学数学,善总结,
勤思考,会表达!我最棒,你最棒,
我们大家都最棒!《一元二次方程》小结课考题再现 关于x的一元二次方程(x-m)2+6x=4m-3有实数根.
(1)求m的取值范围.
(2)设方程的两根分别是x1与x2,求代数式
x12+x22 + x1x2的最小值.(2012年乐山中考题改编)
一、盘点知识、构建体系解题三想:解题前要猜想,解题时要联想,解题后要回想联想一
关于x的一元二次方程的标准形式是:
ax2+bx+c=0(a≠0).联想二关于x的一元二次方程ax2+bx+c=0(a≠0)的根的判别式
是_________ .
Δ=b2-4ac不相等相等没有考题呈现 关于x的一元二次方程(x-m)2+6x=4m-3有实数根.
(1)求m的取值范围.
(2)设方程的两根分别是x1与x2,求代数式
x1x2+x12+x22的最小值.(2012年乐山中考题改编)
一、盘点知识、构建体系联想三 联想四关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1、x2,那么x1+x2=__, x1x2=__,
配方法:分为两类,第一类:当首项系数为1时,直接配一次项系数一半的平方;第二类:若二次项不为1,先把首项系数化为1,在配一次项系数一半的平方。一、盘点知识、构建体系一元二次方程根与系数的关系“拓展积累”:
1.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为1,则有a+b+c=__.
2.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为-1,则有_______.
3.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为0,则有_______.
0a-b+c=0或a+c=bC=0一、盘点知识、构建体系4.二次三项式ax2+bx+c是完全平方式,可以理解为对应的一元二次方程ax2+bx+c=0(a≠0)的_______.“b2-4ac”=05.关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1、x2,则|x1-x2|=____.
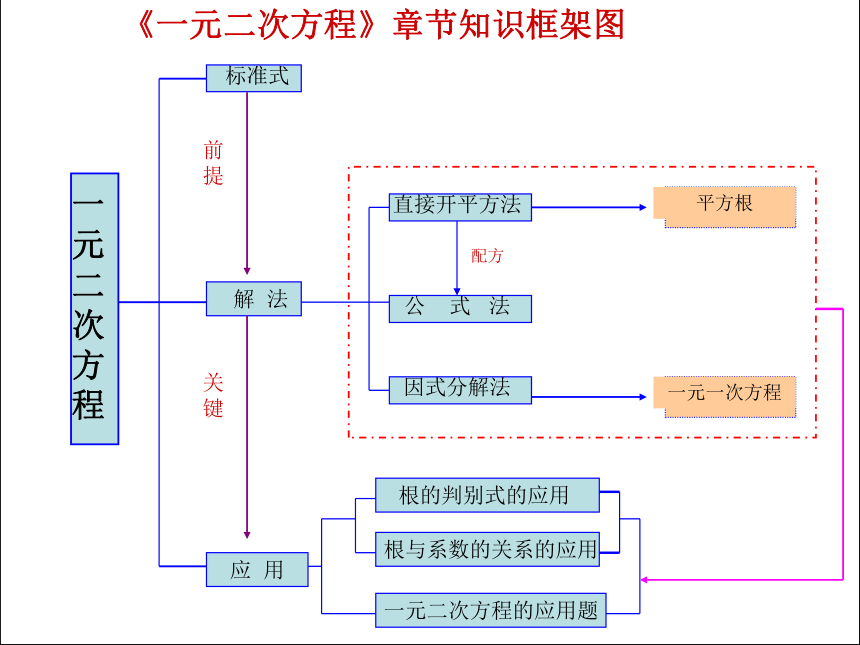
《一元二次方程》章节知识框架图二、解剖病例,提高认识 病例一:关于x的方程 是关于x的一元二次方程,则m的值是正解:(课后自行完成)病例二:方程x2-2x+3=0与方程x2+3x-4=0的所有实数根之和为(D)
A. 1 B.-3 C.5 D. -1 病因:忽视了判别式的符号二、解剖病例,提高认识正解:二、解剖病例,提高认识病例三
关于x的一元二次方程kx2- x+1=0有两个不相等的实数根,则可的取值范围是_____.
病因:忽略了隐含条件解:由题意得, >0,解之得,k<正解:病例四:病因:没有读懂题二、解剖病例,提高认识数学需要阅读三、精讲例题、挖掘内涵 例1. 关于x的一元二次方程x2+2x+m=0.
(1)当m=-3时,求方程的根;
(2)当m=3时,判断方程的根的情况.
变式一:已知x=1是关于x的方程x2+2x+m=0的一个根,则方程的另一根是___.
变式二:若二次三项式x2+2x+m是完全平方式,则m=___.
变式三:关于x的 一元二次方程x2+2x+m=0的两根为x1, x2,且 x12 x2+ x1x22=-3.求m的值.
三、精讲例题、挖掘内涵例2 .关于x的一元二次方程(1-2k)x2- x-1=0有实数根,则可的取值范围是___.
三、例题精讲、挖掘内涵变式一:关于x的一元二次方程(1-2k)x2- x-1=0的两根互为相反数,则k的值是___.
变式二:关于x的方程(1-2k)x2- x-1=0有实数根,则x的取值范围是___.
三、例题精讲、挖掘内涵同类题一:关于x的一元二次方程(m-2)x2+x+m2-4=0的一个根为0,则m的值是___.
同类题二:直角三角形的两条直角边a、b是关于x的方程x2-(m-3)x+(m+2)=0两根,且斜边为5,m的值是_____.
四、反思体味,内省自悟 通过本节课的学习,您有什么收获?还有什么疑惑吗?好题分享:请与您的老师和同学分享一道特色题五、针对训练,整体升华1、把方程 x2-8x-4=0 化成的形式,结果为______2、市政府为了解决市民看病难的问题,决定下调药品价格,某种药品经过连续两次降价后,由每盒200元下调至128元,则这种药品平均每次降价()
(A)10% (B)15% (C)18% (D)20%3、关于x的一元二次方程mx2-(3m-1)x+2m-1=0,其根的判别式的值是1,则m的值是___ 4、等腰三角形三边的长为2、2、,若关于的一元二次方程的两根之差的绝对值为 ,则等腰三角形的周长为 _____ .5、用因式分解法解方程:4(x-2)2-(3x-1)2=0. 6、用配方法解方程:4x2-12x-1=0. 7、用公式法解方程:4x2-3x-1=x-2 8、请用配方法证明关于x的方程ax2+bx+c=0(a≠0)的解为:x=
( )9、若关于的一元二次方x2+(2k-3)x+k2=0有实数根 、 ,(1)求实数的取值范围;(2)设 求t的最小值.
勤思考,会表达!我最棒,你最棒,
我们大家都最棒!《一元二次方程》小结课考题再现 关于x的一元二次方程(x-m)2+6x=4m-3有实数根.
(1)求m的取值范围.
(2)设方程的两根分别是x1与x2,求代数式
x12+x22 + x1x2的最小值.(2012年乐山中考题改编)
一、盘点知识、构建体系解题三想:解题前要猜想,解题时要联想,解题后要回想联想一
关于x的一元二次方程的标准形式是:
ax2+bx+c=0(a≠0).联想二关于x的一元二次方程ax2+bx+c=0(a≠0)的根的判别式
是_________ .
Δ=b2-4ac不相等相等没有考题呈现 关于x的一元二次方程(x-m)2+6x=4m-3有实数根.
(1)求m的取值范围.
(2)设方程的两根分别是x1与x2,求代数式
x1x2+x12+x22的最小值.(2012年乐山中考题改编)
一、盘点知识、构建体系联想三 联想四关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1、x2,那么x1+x2=__, x1x2=__,
配方法:分为两类,第一类:当首项系数为1时,直接配一次项系数一半的平方;第二类:若二次项不为1,先把首项系数化为1,在配一次项系数一半的平方。一、盘点知识、构建体系一元二次方程根与系数的关系“拓展积累”:
1.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为1,则有a+b+c=__.
2.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为-1,则有_______.
3.关于x的一元二次方程ax2+bx+c=0(a≠0) 有一根为0,则有_______.
0a-b+c=0或a+c=bC=0一、盘点知识、构建体系4.二次三项式ax2+bx+c是完全平方式,可以理解为对应的一元二次方程ax2+bx+c=0(a≠0)的_______.“b2-4ac”=05.关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1、x2,则|x1-x2|=____.
《一元二次方程》章节知识框架图二、解剖病例,提高认识 病例一:关于x的方程 是关于x的一元二次方程,则m的值是正解:(课后自行完成)病例二:方程x2-2x+3=0与方程x2+3x-4=0的所有实数根之和为(D)
A. 1 B.-3 C.5 D. -1 病因:忽视了判别式的符号二、解剖病例,提高认识正解:二、解剖病例,提高认识病例三
关于x的一元二次方程kx2- x+1=0有两个不相等的实数根,则可的取值范围是_____.
病因:忽略了隐含条件解:由题意得, >0,解之得,k<正解:病例四:病因:没有读懂题二、解剖病例,提高认识数学需要阅读三、精讲例题、挖掘内涵 例1. 关于x的一元二次方程x2+2x+m=0.
(1)当m=-3时,求方程的根;
(2)当m=3时,判断方程的根的情况.
变式一:已知x=1是关于x的方程x2+2x+m=0的一个根,则方程的另一根是___.
变式二:若二次三项式x2+2x+m是完全平方式,则m=___.
变式三:关于x的 一元二次方程x2+2x+m=0的两根为x1, x2,且 x12 x2+ x1x22=-3.求m的值.
三、精讲例题、挖掘内涵例2 .关于x的一元二次方程(1-2k)x2- x-1=0有实数根,则可的取值范围是___.
三、例题精讲、挖掘内涵变式一:关于x的一元二次方程(1-2k)x2- x-1=0的两根互为相反数,则k的值是___.
变式二:关于x的方程(1-2k)x2- x-1=0有实数根,则x的取值范围是___.
三、例题精讲、挖掘内涵同类题一:关于x的一元二次方程(m-2)x2+x+m2-4=0的一个根为0,则m的值是___.
同类题二:直角三角形的两条直角边a、b是关于x的方程x2-(m-3)x+(m+2)=0两根,且斜边为5,m的值是_____.
四、反思体味,内省自悟 通过本节课的学习,您有什么收获?还有什么疑惑吗?好题分享:请与您的老师和同学分享一道特色题五、针对训练,整体升华1、把方程 x2-8x-4=0 化成的形式,结果为______2、市政府为了解决市民看病难的问题,决定下调药品价格,某种药品经过连续两次降价后,由每盒200元下调至128元,则这种药品平均每次降价()
(A)10% (B)15% (C)18% (D)20%3、关于x的一元二次方程mx2-(3m-1)x+2m-1=0,其根的判别式的值是1,则m的值是___ 4、等腰三角形三边的长为2、2、,若关于的一元二次方程的两根之差的绝对值为 ,则等腰三角形的周长为 _____ .5、用因式分解法解方程:4(x-2)2-(3x-1)2=0. 6、用配方法解方程:4x2-12x-1=0. 7、用公式法解方程:4x2-3x-1=x-2 8、请用配方法证明关于x的方程ax2+bx+c=0(a≠0)的解为:x=
( )9、若关于的一元二次方x2+(2k-3)x+k2=0有实数根 、 ,(1)求实数的取值范围;(2)设 求t的最小值.
