物理人教版(2019)必修第一册3.5共点力的平衡(共40张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册3.5共点力的平衡(共40张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-08 18:40:02 | ||
图片预览





文档简介
(共40张PPT)
3.5 共点力的平衡
G
FN
G
F1
F2
G
FN
F
Ff
F1
F2
F
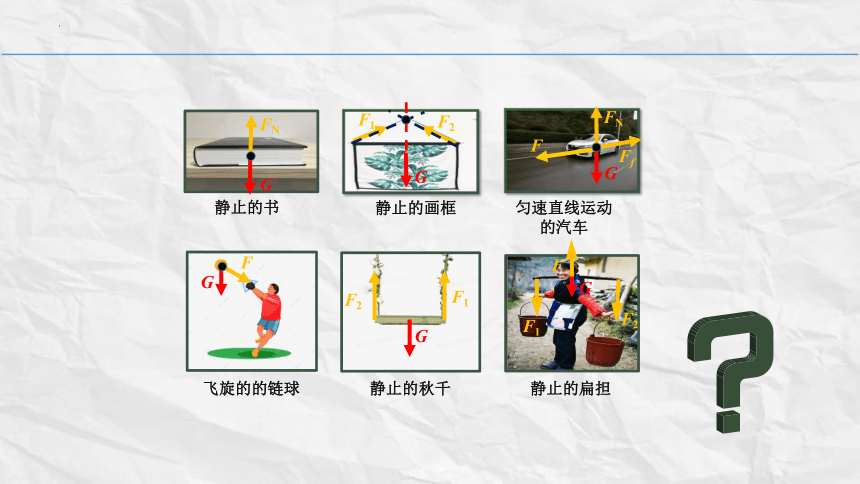
静止的书
静止的画框
飞旋的的链球
静止的秋千
静止的扁担
匀速直线运动的汽车
G
F1
F2
G
F
G
G
FN
G
F1
F2
G
FN
F
Ff
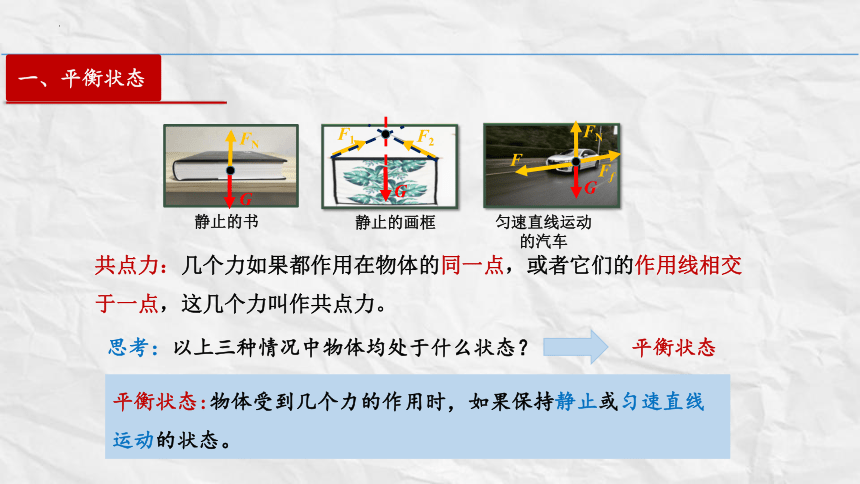
静止的书
静止的画框
匀速直线运动的汽车
共点力:几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
思考:以上三种情况中物体均处于什么状态?
平衡状态
一、平衡状态
平衡状态:物体受到几个力的作用时,如果保持静止或匀速直线运动的状态。
一、平衡状态
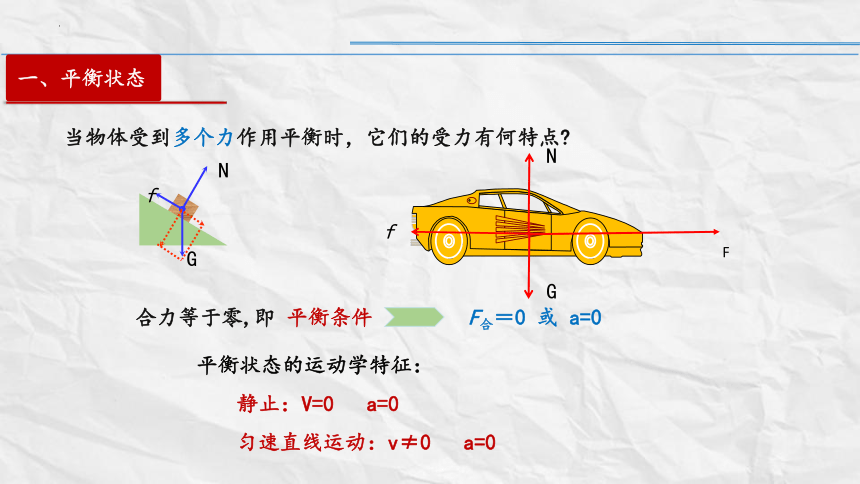
当物体受到多个力作用平衡时,它们的受力有何特点
G
N
f
F
N
G
f
合力等于零,即 平衡条件
平衡状态的运动学特征: 静止:V=0 a=0 匀速直线运动:v≠0 a=0
F合=0 或 a=0
一、平衡状态
“静止”=“v=0”
v=0
a=0时,静止,处于平衡状态
a≠0时,不静止,处于非平衡状态,如自由落体初始时刻、竖直上抛
注意:保持静止和瞬时速度为0意义不同
一、平衡状态
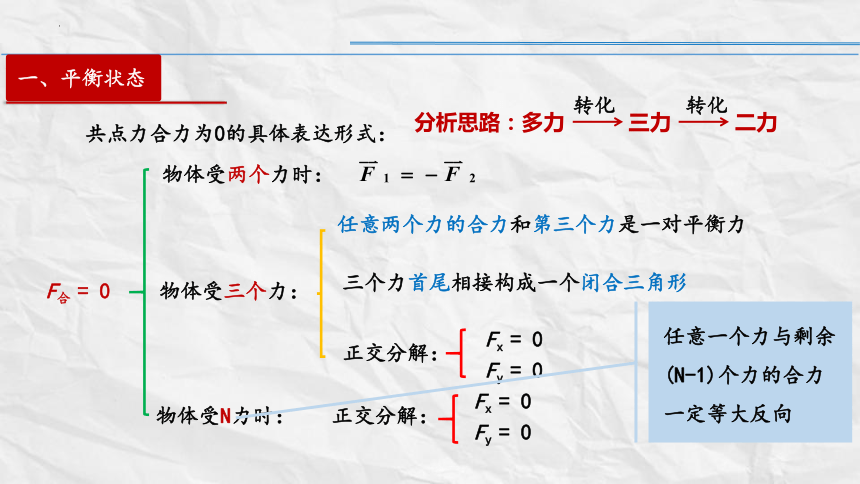
共点力合力为0的具体表达形式:
F合 = 0
物体受三个力:
三个力首尾相接构成一个闭合三角形
任意两个力的合力和第三个力是一对平衡力
正交分解:
Fx = 0
Fy = 0
物体受N力时:
正交分解:
Fx = 0
Fy = 0
物体受两个力时:
任意一个力与剩余(N-1)个力的合力一定等大反向
分析思路:多力 三力 二力
转化
转化
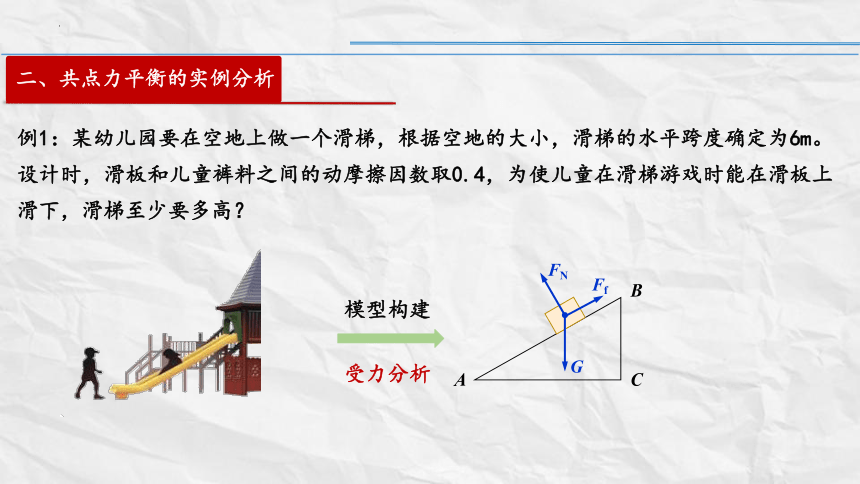
例1:某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
二、共点力平衡的实例分析
二、共点力平衡的实例分析
A
B
C
方法一:正交分解法
Ff=μFN
解得:tanθ =μ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
G1
G2
二、共点力平衡的实例分析
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等大反向
方法二:合成法
Ff=μFN
解得 tanθ =μ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
FN
G
G’
Ff
A
B
C
θ
θ
G
Ff
FN
二、共点力平衡的实例分析
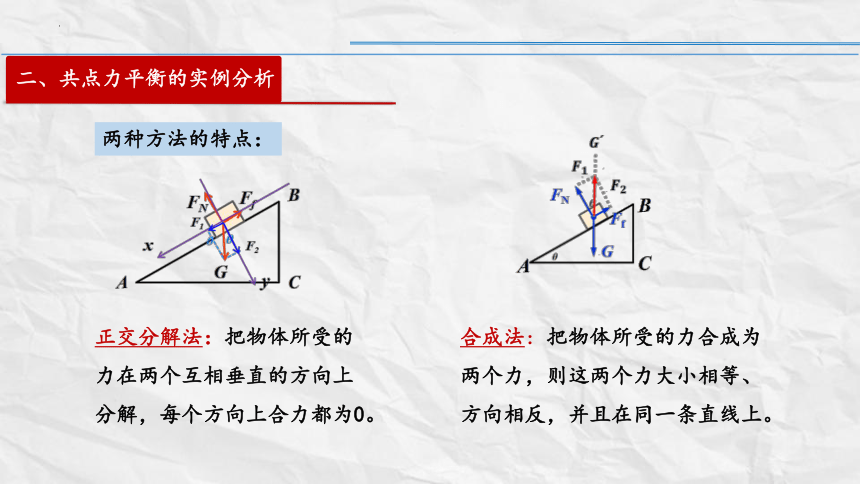
合成法:把物体所受的力合成为两个力,则这两个力大小相等、方向相反,并且在同一条直线上。
正交分解法:把物体所受的力在两个互相垂直的方向上分解,每个方向上合力都为0。
两种方法的特点:
二、共点力平衡的实例分析
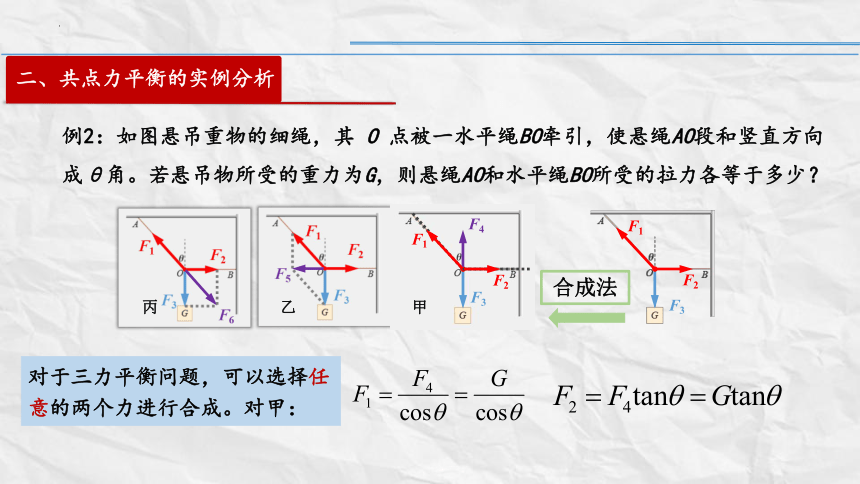
例2:如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
F3
F2
F1
合成法
F3
F2
F1
F5
F3
F2
F1
F6
乙
丙
F3
F1
F2
F4
甲
对于三力平衡问题,可以选择任意的两个力进行合成。对甲:
二、共点力平衡的实例分析
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
三、处理平衡问题的常用方法
方法 内容
合成法 物体受三个共点力的作用而平衡,则任意两个力的合力一定与第三个力大小相等,方向相反
分解法 物体受三个共点力的作用而平衡,将某一个力按力的效果分解,则其分力和其他两个力满足平衡条件
正交分 解法 物体受到三个或三个以上力的作用时,将物体所受的力分解为相互垂直的两组,每组力都满足平衡条件
力的三角形法 对受三力作用而平衡的物体,将力的矢量图平移使三力组成一个首尾依次相接的矢量三角形,根据正弦定理、余弦定理或相似三角形等数学知识求解未知力
应用共点力平衡条件解题的步骤:
合成法、分解法、正交分解法
根据平衡条件列出平衡方程,解平衡方程,对结果进行讨论
选取一个平衡体(单个物体或系统,也可以是结点)作为研究对象
对研究对象进行受力分析,画出受力示意图
1.选择研究对象
2.画受力示意图
3.明确解题策略
4.列方程求解
三、处理平衡问题的常用方法
四、整体法、隔离法求解平衡问题
(1)整体法:对物理问题的整个系统或整个过程进行分析、研究的方法。
(2)整体法和隔离法的应用:在分析外力对系统的作用时,用整体法;在分析系统内各物体(或一个物体的各部分)间的相互作用时,用隔离法;有时解答一个问题需要多次选取研究对象,整体法和隔离法交替应用。
四、整体法、隔离法求解平衡问题
例:如图所示,甲、乙两个小球的质量均为m,两球间用细线2连接,甲球用细线1悬挂在天花板上。现分别用大小相等的力F水平向左、向右拉两球,平衡时细线都被拉紧。则平衡时两球的可能位置是下列选项中的( )
A
谢谢!
3.5 共点力的平衡(第2课时)
物 理
一、“定杆”与“动杆、“活结”与“死结”
绳子的“死结”和“活结”
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
一、“定杆”与“动杆”、“活结”与“死结”
“死结”:两根独立的绳子,力可以不同。
轻绳问题小结:
“活结”:两侧的绳子作用力一定等大。
两侧绳子合力的方向一定沿这两段绳子夹角的平分线。
一、“定杆”与“动杆”、“活结”与“死结”
例:如图所示,将一轻质细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是( )
C
一、“定杆”与“动杆”、“活结”与“死结”
晾衣杆模型:
一、“定杆”与“动杆”、“活结”与“死结”
如图,晒衣服的绳子轻且光滑,悬挂衣服的衣架的挂钩也是光滑的,轻绳两端分别固定在两根竖直杆上的A、B两点,衣服处于静止状态,如果保持绳子A端位置不变,将B端分别移动到不同的位置。
下列判断正确的是( )
A.B端移到B1位置时,绳子张力不变
B.B端移到B2位置时,绳子张力变小
C.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变大
D.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变小
AD
一、“定杆”与“动杆”、“活结”与“死结”
一、“定杆”与“动杆”、“活结”与“死结”
“定杆”与“动杆”
(1)“动杆”:对于一端有转轴或有铰链的轻杆,当杆处于平衡状态时,杆所受到的弹力方向一定沿着轻杆的方向,否则会引起杆的转动,如甲图所示。
(2)“定杆”:一端固定的轻杆(如一端“插入”墙壁或固定于地面),杆所受到的弹力不一定沿着轻杆的方向,力的方向只能根据具体情况进行受力分析。需要根据平衡条件确定杆中的弹力大小和方向。如乙图所示。
甲图
乙图
一、“定杆”与“动杆”、“活结”与“死结”
BD
一、“定杆”与“动杆、“活结”与“死结”
例:如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量为M2的物体,已知物体重力加速度为g。求:(1)轻杆BC对C端的弹力大小及方向;(2)轻杆HG对G端的弹力大小及方向。
θ
G2= G cosθ
G
G1
G2
θ
θ
F1
F2
G
θ
G1= G sinθ
F1= G tanθ
F2= G/cosθ
使物体紧压挡板
使物体紧压斜面
那挡板缓慢旋转的过程中呢?
二、动态平衡
二、动态平衡
动态平衡问题是指通过控制某些物理量的变化,使物体的状态发生缓慢改变,“缓慢”指物体的速度很小,可认为速度为零,所以在变化程中可认为物体处于平衡状态,把物体的这种状态称为动态平衡态。
二、动态平衡
1、解析式法
解析:此时FN1=mgtanθ ;FN2=mg/cosθ
θ变小:tanθ变小;cosθ变大;FN1变小;FN2 变小
如图所示,一质量为m的光滑小球,静止在挡板和倾角为θ的斜面之间。现将斜面以下端顶点为轴转动(挡板保持竖直状态不变),使θ角变小(θ>0)的过程中,问:挡板对小球的支持力FN1和斜面对小球的支持力FN2大小如何变化?
mg
FN1
F
θ
FN2
二、动态平衡
如图所示,一质量为m的光滑小球,静止在挡板和倾角为θ的斜面之间。现将挡板以下端为轴缓慢逆时针转动直至放平的过程中,问:挡板对小球的支持力FN1和斜面对小球的支持力FN2大小如何变化?
FN1
FN2
α
mg
二、动态平衡
2、动态矢量三角形法(图解法)适用于三力动态平衡:一力大小方向均不变(通常为重力,也可能是其他力)、一力方向不变、一力大小方向都变。
解题方法:构建物体受力三角形,将三个力的首尾相连构成闭合三角形;画力的三角形初、末状态图,分析另外两个力的变化情况。
二、动态平衡
θ
mg
FN1
挡板缓慢转动至放平,FN2减小到0,FN1先减小后增大到mg
FN1
FN2
mg
FN2
FN1
α
FN1
FN2
mg
二、动态平衡
当FN1 垂直于FN2时,FN1存在最小值,最小值FN1min=mgsinθ
θ
mg
FN1
FN1
FN2
结论:变化力垂直于定向力时,变化力有最小值。
挡板对物体的支持力FN1(变化力)先变小后变大。
斜面对物体的支持力FN2(定向力)一直变小。
二、动态平衡
3、相似三角形法:在三力平衡问题中,各力构成的矢量三角形可能不是直角三角形,力与力之间的夹角可能也未知,但题目中能找出几何三角形和力所构成的三角形相似,此时可利用相似三角形的对应边成比例进行求解。
适用条件:有一恒力,另外两个力大小、方向都变。
解题思路:①将物体所受三个力的矢量首尾相连构成闭合三角形,寻找与力的三角形相似的实际物体组成的几何三角形;②利用相似三角形的性质,建立比例关系,把力的大小变化转化成三角形边长的大小变化。
二、动态平衡
受力特点:三个力互相不垂直,且夹角(方向)未知。
如图,半径为R的光滑半球的正上方,离球面顶端距离为h 的O点,用一根长为l的细线悬挂质量为m 的小球,小球靠在半球面上.试求小球对球面压力的大小
F
N
G
相似三角形法:力的矢量三角形与空间三角形相似
T
由于拉动过程中h、R不变,L变小。故T减小,FN不变
二、动态平衡
4、作辅助圆法:
对于三个共点力作用下的动态平衡问题,若有其中一个力大小、方向均确定,另两个力的方向在变化,但是方向变化的两个力的夹角保持不变,可以建立辅助圆,用“同弧所对圆周角相等”的规律解题。
二、动态平衡
5、拉密定理法:物体受到三个共点力作用保持平衡状态,当某个力发生变化时,判断各个力的大小变化情况。
方法:在同一平面内,当三个共点力的合力为零时,其中任一个力与其他两个力夹角正弦的比值相等
二、动态平衡
如图所示,两根轻绳一端系于结点O,另一端分别系于固定圆环上的A、B两点,O为圆心。O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与绳OA成120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角始终不变,物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
A. F1逐渐增大
B. F1先增大后减小
C. F2逐渐增大
D. F2先减小后增大
O
A
M
B
谢谢!
3.5 共点力的平衡
G
FN
G
F1
F2
G
FN
F
Ff
F1
F2
F
静止的书
静止的画框
飞旋的的链球
静止的秋千
静止的扁担
匀速直线运动的汽车
G
F1
F2
G
F
G
G
FN
G
F1
F2
G
FN
F
Ff
静止的书
静止的画框
匀速直线运动的汽车
共点力:几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
思考:以上三种情况中物体均处于什么状态?
平衡状态
一、平衡状态
平衡状态:物体受到几个力的作用时,如果保持静止或匀速直线运动的状态。
一、平衡状态
当物体受到多个力作用平衡时,它们的受力有何特点
G
N
f
F
N
G
f
合力等于零,即 平衡条件
平衡状态的运动学特征: 静止:V=0 a=0 匀速直线运动:v≠0 a=0
F合=0 或 a=0
一、平衡状态
“静止”=“v=0”
v=0
a=0时,静止,处于平衡状态
a≠0时,不静止,处于非平衡状态,如自由落体初始时刻、竖直上抛
注意:保持静止和瞬时速度为0意义不同
一、平衡状态
共点力合力为0的具体表达形式:
F合 = 0
物体受三个力:
三个力首尾相接构成一个闭合三角形
任意两个力的合力和第三个力是一对平衡力
正交分解:
Fx = 0
Fy = 0
物体受N力时:
正交分解:
Fx = 0
Fy = 0
物体受两个力时:
任意一个力与剩余(N-1)个力的合力一定等大反向
分析思路:多力 三力 二力
转化
转化
例1:某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
二、共点力平衡的实例分析
二、共点力平衡的实例分析
A
B
C
方法一:正交分解法
Ff=μFN
解得:tanθ =μ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
G1
G2
二、共点力平衡的实例分析
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等大反向
方法二:合成法
Ff=μFN
解得 tanθ =μ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
FN
G
G’
Ff
A
B
C
θ
θ
G
Ff
FN
二、共点力平衡的实例分析
合成法:把物体所受的力合成为两个力,则这两个力大小相等、方向相反,并且在同一条直线上。
正交分解法:把物体所受的力在两个互相垂直的方向上分解,每个方向上合力都为0。
两种方法的特点:
二、共点力平衡的实例分析
例2:如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
F3
F2
F1
合成法
F3
F2
F1
F5
F3
F2
F1
F6
乙
丙
F3
F1
F2
F4
甲
对于三力平衡问题,可以选择任意的两个力进行合成。对甲:
二、共点力平衡的实例分析
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
三、处理平衡问题的常用方法
方法 内容
合成法 物体受三个共点力的作用而平衡,则任意两个力的合力一定与第三个力大小相等,方向相反
分解法 物体受三个共点力的作用而平衡,将某一个力按力的效果分解,则其分力和其他两个力满足平衡条件
正交分 解法 物体受到三个或三个以上力的作用时,将物体所受的力分解为相互垂直的两组,每组力都满足平衡条件
力的三角形法 对受三力作用而平衡的物体,将力的矢量图平移使三力组成一个首尾依次相接的矢量三角形,根据正弦定理、余弦定理或相似三角形等数学知识求解未知力
应用共点力平衡条件解题的步骤:
合成法、分解法、正交分解法
根据平衡条件列出平衡方程,解平衡方程,对结果进行讨论
选取一个平衡体(单个物体或系统,也可以是结点)作为研究对象
对研究对象进行受力分析,画出受力示意图
1.选择研究对象
2.画受力示意图
3.明确解题策略
4.列方程求解
三、处理平衡问题的常用方法
四、整体法、隔离法求解平衡问题
(1)整体法:对物理问题的整个系统或整个过程进行分析、研究的方法。
(2)整体法和隔离法的应用:在分析外力对系统的作用时,用整体法;在分析系统内各物体(或一个物体的各部分)间的相互作用时,用隔离法;有时解答一个问题需要多次选取研究对象,整体法和隔离法交替应用。
四、整体法、隔离法求解平衡问题
例:如图所示,甲、乙两个小球的质量均为m,两球间用细线2连接,甲球用细线1悬挂在天花板上。现分别用大小相等的力F水平向左、向右拉两球,平衡时细线都被拉紧。则平衡时两球的可能位置是下列选项中的( )
A
谢谢!
3.5 共点力的平衡(第2课时)
物 理
一、“定杆”与“动杆、“活结”与“死结”
绳子的“死结”和“活结”
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
一、“定杆”与“动杆”、“活结”与“死结”
“死结”:两根独立的绳子,力可以不同。
轻绳问题小结:
“活结”:两侧的绳子作用力一定等大。
两侧绳子合力的方向一定沿这两段绳子夹角的平分线。
一、“定杆”与“动杆”、“活结”与“死结”
例:如图所示,将一轻质细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是( )
C
一、“定杆”与“动杆”、“活结”与“死结”
晾衣杆模型:
一、“定杆”与“动杆”、“活结”与“死结”
如图,晒衣服的绳子轻且光滑,悬挂衣服的衣架的挂钩也是光滑的,轻绳两端分别固定在两根竖直杆上的A、B两点,衣服处于静止状态,如果保持绳子A端位置不变,将B端分别移动到不同的位置。
下列判断正确的是( )
A.B端移到B1位置时,绳子张力不变
B.B端移到B2位置时,绳子张力变小
C.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变大
D.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变小
AD
一、“定杆”与“动杆”、“活结”与“死结”
一、“定杆”与“动杆”、“活结”与“死结”
“定杆”与“动杆”
(1)“动杆”:对于一端有转轴或有铰链的轻杆,当杆处于平衡状态时,杆所受到的弹力方向一定沿着轻杆的方向,否则会引起杆的转动,如甲图所示。
(2)“定杆”:一端固定的轻杆(如一端“插入”墙壁或固定于地面),杆所受到的弹力不一定沿着轻杆的方向,力的方向只能根据具体情况进行受力分析。需要根据平衡条件确定杆中的弹力大小和方向。如乙图所示。
甲图
乙图
一、“定杆”与“动杆”、“活结”与“死结”
BD
一、“定杆”与“动杆、“活结”与“死结”
例:如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量为M2的物体,已知物体重力加速度为g。求:(1)轻杆BC对C端的弹力大小及方向;(2)轻杆HG对G端的弹力大小及方向。
θ
G2= G cosθ
G
G1
G2
θ
θ
F1
F2
G
θ
G1= G sinθ
F1= G tanθ
F2= G/cosθ
使物体紧压挡板
使物体紧压斜面
那挡板缓慢旋转的过程中呢?
二、动态平衡
二、动态平衡
动态平衡问题是指通过控制某些物理量的变化,使物体的状态发生缓慢改变,“缓慢”指物体的速度很小,可认为速度为零,所以在变化程中可认为物体处于平衡状态,把物体的这种状态称为动态平衡态。
二、动态平衡
1、解析式法
解析:此时FN1=mgtanθ ;FN2=mg/cosθ
θ变小:tanθ变小;cosθ变大;FN1变小;FN2 变小
如图所示,一质量为m的光滑小球,静止在挡板和倾角为θ的斜面之间。现将斜面以下端顶点为轴转动(挡板保持竖直状态不变),使θ角变小(θ>0)的过程中,问:挡板对小球的支持力FN1和斜面对小球的支持力FN2大小如何变化?
mg
FN1
F
θ
FN2
二、动态平衡
如图所示,一质量为m的光滑小球,静止在挡板和倾角为θ的斜面之间。现将挡板以下端为轴缓慢逆时针转动直至放平的过程中,问:挡板对小球的支持力FN1和斜面对小球的支持力FN2大小如何变化?
FN1
FN2
α
mg
二、动态平衡
2、动态矢量三角形法(图解法)适用于三力动态平衡:一力大小方向均不变(通常为重力,也可能是其他力)、一力方向不变、一力大小方向都变。
解题方法:构建物体受力三角形,将三个力的首尾相连构成闭合三角形;画力的三角形初、末状态图,分析另外两个力的变化情况。
二、动态平衡
θ
mg
FN1
挡板缓慢转动至放平,FN2减小到0,FN1先减小后增大到mg
FN1
FN2
mg
FN2
FN1
α
FN1
FN2
mg
二、动态平衡
当FN1 垂直于FN2时,FN1存在最小值,最小值FN1min=mgsinθ
θ
mg
FN1
FN1
FN2
结论:变化力垂直于定向力时,变化力有最小值。
挡板对物体的支持力FN1(变化力)先变小后变大。
斜面对物体的支持力FN2(定向力)一直变小。
二、动态平衡
3、相似三角形法:在三力平衡问题中,各力构成的矢量三角形可能不是直角三角形,力与力之间的夹角可能也未知,但题目中能找出几何三角形和力所构成的三角形相似,此时可利用相似三角形的对应边成比例进行求解。
适用条件:有一恒力,另外两个力大小、方向都变。
解题思路:①将物体所受三个力的矢量首尾相连构成闭合三角形,寻找与力的三角形相似的实际物体组成的几何三角形;②利用相似三角形的性质,建立比例关系,把力的大小变化转化成三角形边长的大小变化。
二、动态平衡
受力特点:三个力互相不垂直,且夹角(方向)未知。
如图,半径为R的光滑半球的正上方,离球面顶端距离为h 的O点,用一根长为l的细线悬挂质量为m 的小球,小球靠在半球面上.试求小球对球面压力的大小
F
N
G
相似三角形法:力的矢量三角形与空间三角形相似
T
由于拉动过程中h、R不变,L变小。故T减小,FN不变
二、动态平衡
4、作辅助圆法:
对于三个共点力作用下的动态平衡问题,若有其中一个力大小、方向均确定,另两个力的方向在变化,但是方向变化的两个力的夹角保持不变,可以建立辅助圆,用“同弧所对圆周角相等”的规律解题。
二、动态平衡
5、拉密定理法:物体受到三个共点力作用保持平衡状态,当某个力发生变化时,判断各个力的大小变化情况。
方法:在同一平面内,当三个共点力的合力为零时,其中任一个力与其他两个力夹角正弦的比值相等
二、动态平衡
如图所示,两根轻绳一端系于结点O,另一端分别系于固定圆环上的A、B两点,O为圆心。O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与绳OA成120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角始终不变,物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
A. F1逐渐增大
B. F1先增大后减小
C. F2逐渐增大
D. F2先减小后增大
O
A
M
B
谢谢!
