华师大版八年级数学下册课件:14.1 勾股定理(共17张PPT)
文档属性
| 名称 | 华师大版八年级数学下册课件:14.1 勾股定理(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 801.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-14 07:36:26 | ||
图片预览



文档简介
课件17张PPT。勾股定理学习目标:
1.探索勾股定理,感受数形结合思想;
2.尝试验证勾股定理,感受勾股定理的文化价值;
3.初步运用勾股定理,进一步了解和熟悉勾股定理;
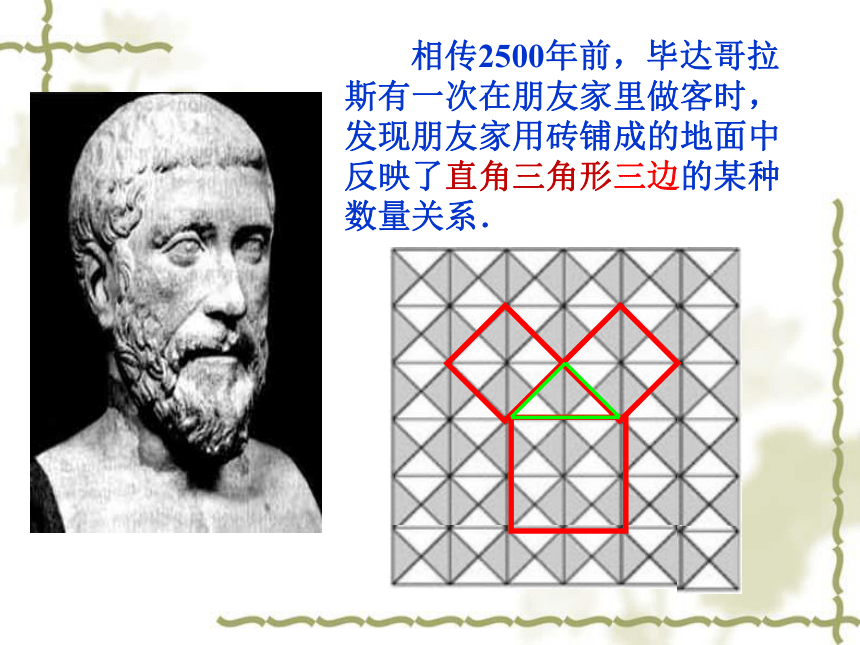
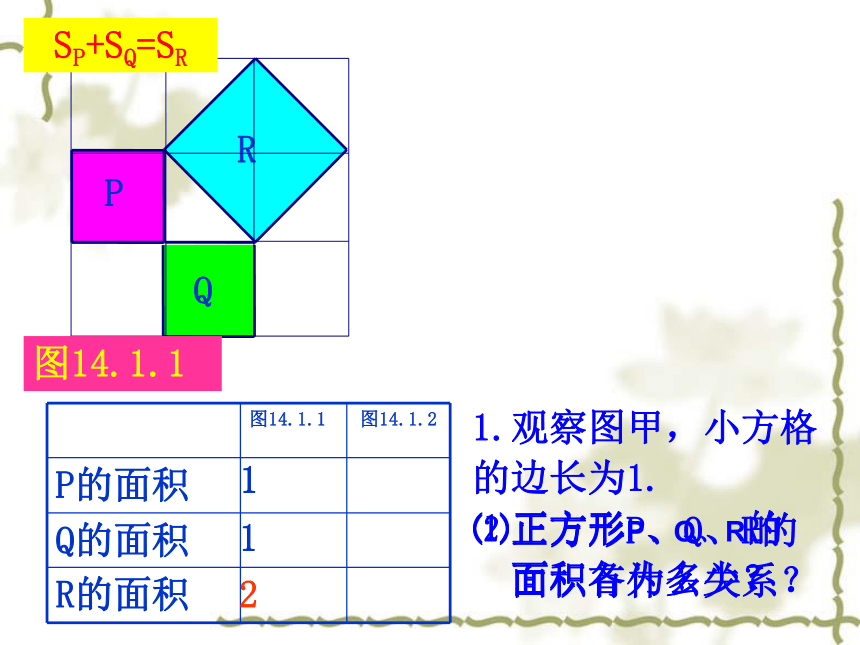
?这就是本届大会会徽的图案. 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.112SP+SQ=SRC图14.1.11.观察图甲,小方格
的边长为1.
⑴正方形P、Q、R的
面积各为多少?⑵正方形P、Q、R的
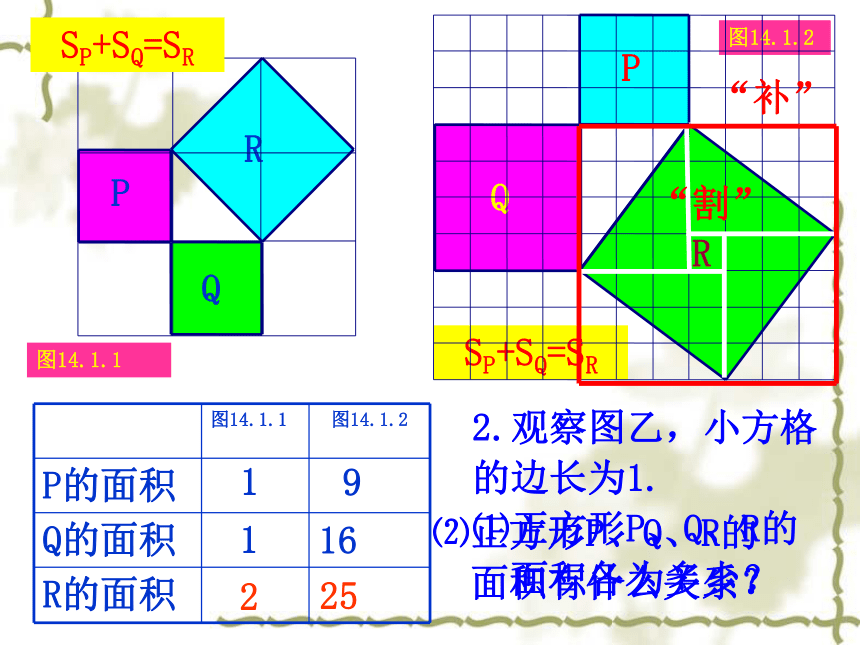
面积有什么关系?C图14.1.22.观察图乙,小方格
的边长为1.
⑴正方形P、Q、R的
面积各为多少?91625SP+SQ=SR⑵正方形P、Q、R的
面积有什么关系?112“割”“补”图14.1.22.观察图乙,小方格
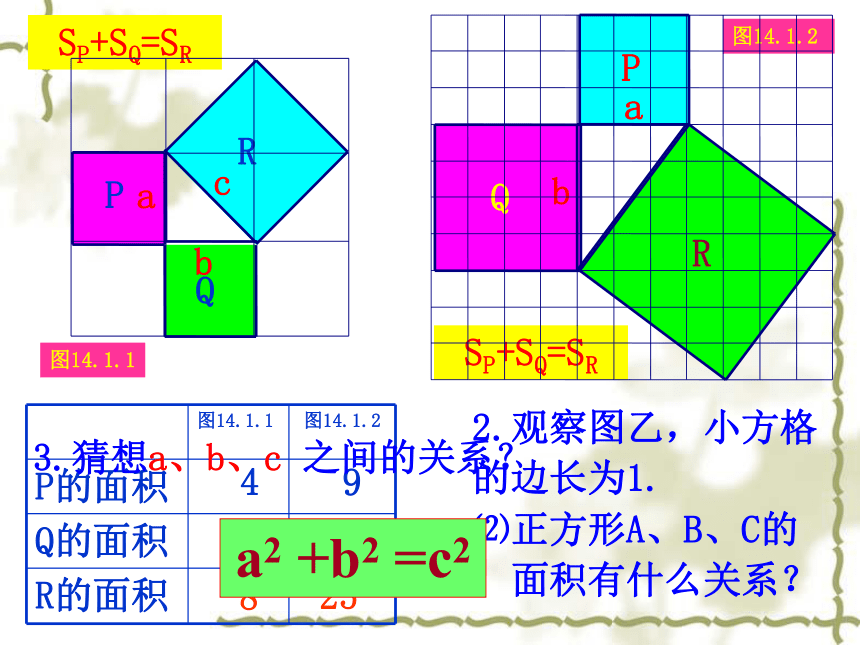
的边长为1.91625SP+SQ=SR⑵正方形A、B、C的
面积有什么关系?448SP+SQ=SR图14.1.1acabcb3.猜想a、b、c 之间的关系?a2 +b2 =c2勾股定理(毕达哥拉斯定理) (gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么 直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股即 :勾2+股2=弦2bac勾股定理的证明(一)大正方形的面积可以表示为 ;
也可以表示为 。(a+b)2所以c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 1、求出下列直角三角形中未知边的长度x。6x25248X
试一试: 2.如图,在Rt△ABC中,∠C=90°.
(1) 已知:c=13,b=5,求 a;
(2) 已知: a:b=3:4, c=15,求a、b.(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结试一试:5 或 1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .当堂评价
2、 如图,点E在正方形ABCD内,且∠AEB=90°,
AE=5,BE=12,求阴影部分的面积.
当堂评价解:在Rt△ABE中, ∠AEB=90°,
AE=5,BE=12
∴ AB2=AE2+BE2=52+122=25+144=169
AB=13
∵正方形ABCD的面积为 AB2=169;
Rt △ABE的面积为
∴阴影部分面积为 169-30=139
1、这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 、运用“勾股定理”应注意什么问题?1、课本111页练习1、2;117页习题
第1、2题。作业2、查阅有关勾股定理的历史资料。 3.(选做) 已知等腰直角三角形斜边的长为2cm,求这个三角形的周长? 再见
1.探索勾股定理,感受数形结合思想;
2.尝试验证勾股定理,感受勾股定理的文化价值;
3.初步运用勾股定理,进一步了解和熟悉勾股定理;
?这就是本届大会会徽的图案. 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.112SP+SQ=SRC图14.1.11.观察图甲,小方格
的边长为1.
⑴正方形P、Q、R的
面积各为多少?⑵正方形P、Q、R的
面积有什么关系?C图14.1.22.观察图乙,小方格
的边长为1.
⑴正方形P、Q、R的
面积各为多少?91625SP+SQ=SR⑵正方形P、Q、R的
面积有什么关系?112“割”“补”图14.1.22.观察图乙,小方格
的边长为1.91625SP+SQ=SR⑵正方形A、B、C的
面积有什么关系?448SP+SQ=SR图14.1.1acabcb3.猜想a、b、c 之间的关系?a2 +b2 =c2勾股定理(毕达哥拉斯定理) (gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么 直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股即 :勾2+股2=弦2bac勾股定理的证明(一)大正方形的面积可以表示为 ;
也可以表示为 。(a+b)2所以c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 1、求出下列直角三角形中未知边的长度x。6x25248X
试一试: 2.如图,在Rt△ABC中,∠C=90°.
(1) 已知:c=13,b=5,求 a;
(2) 已知: a:b=3:4, c=15,求a、b.(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结试一试:5 或 1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .当堂评价
2、 如图,点E在正方形ABCD内,且∠AEB=90°,
AE=5,BE=12,求阴影部分的面积.
当堂评价解:在Rt△ABE中, ∠AEB=90°,
AE=5,BE=12
∴ AB2=AE2+BE2=52+122=25+144=169
AB=13
∵正方形ABCD的面积为 AB2=169;
Rt △ABE的面积为
∴阴影部分面积为 169-30=139
1、这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 、运用“勾股定理”应注意什么问题?1、课本111页练习1、2;117页习题
第1、2题。作业2、查阅有关勾股定理的历史资料。 3.(选做) 已知等腰直角三角形斜边的长为2cm,求这个三角形的周长? 再见
