人教版七年级数学下册课件:5.3.1平行线的性质(共14张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.3.1平行线的性质(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-14 00:00:00 | ||
图片预览





文档简介
课件14张PPT。一、创设情境:问题:
现有一个梯形池塘,但有两个底角处都填满了土,只剩下两个完整的角,你能否设法求出该梯形池塘的四个角各是多少度吗?
5.3.1 平行线的性质二、协同探索:1、利用坐标纸上的直线,或者用直尺和三角尺,画出两条平行线a∥b,
2、画一条截线c,使之与直线a、b相交,
3、并找出一组同位角,标记为 ∠ 1 和∠ 2.
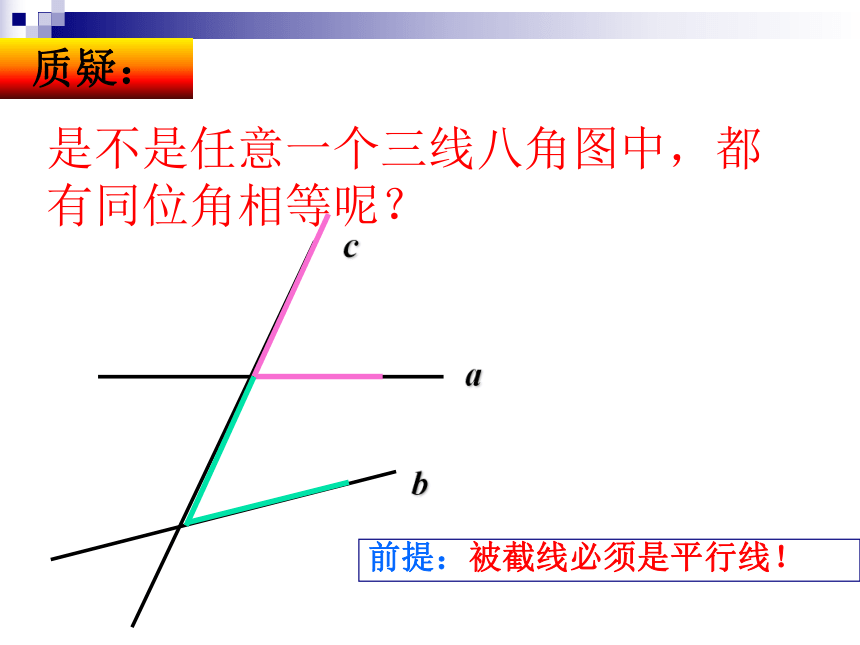
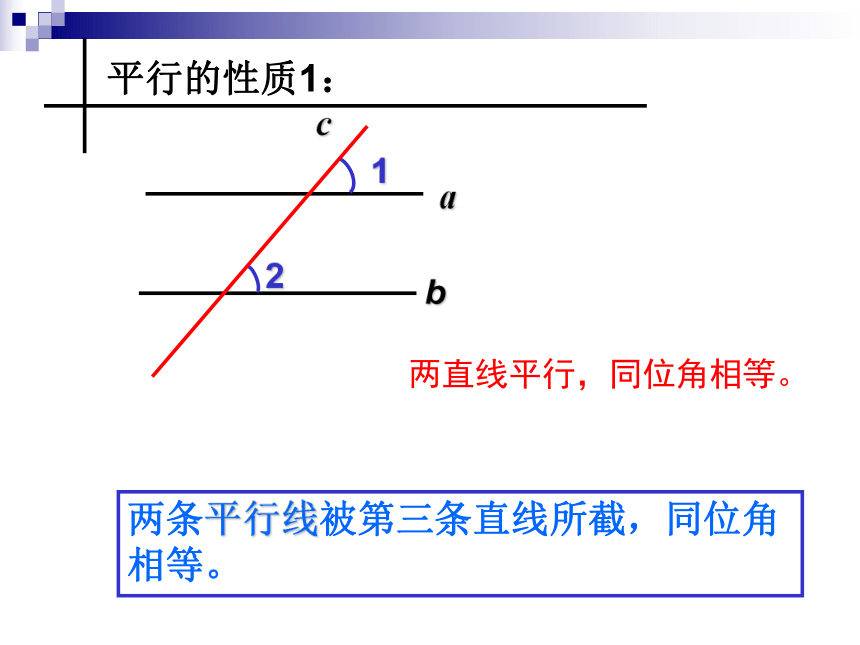
4、用量角器测量这一组同位角的大小,记录下来.从中你能发现什么?几何画板演示动动手!是不是任意一个三线八角图中,都有同位角相等呢?质疑:abc前提:被截线必须是平行线!两条平行线被第三条直线所截,同位角相等。ab21c平行的性质1:两直线平行,同位角相等。 如图,已知:a// b ,那么?3与?2有什么数量关系?
试说明理由! c如图:已知a//b,那么?2与? 4有什么数量关系呢?
试说明理由!思考1思考2小组讨论!动动脑!如图,已知:a// b ,那么?3与?2有什么关系? 答:∠ 2 = ∠3,理由如下:
因为 a∥b(已知),
所以 ∠1= ∠2( ),
因为∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等∠1思考1∠2和∠3是内错角 两条平行线被第三条直线所截,内错角相等。平行的性质2:cc如图:已知a//b,那么?2与? 4有什么关系呢????答: ? 2+ ? 4=180°,理由如下:
a//b (已知)
? 1= ? 2
(两直线平行,同位角相等)
? 1+ ? 4=180°
(邻补角定义)
? 2+ ? 4=180°
(等量代换)?∠2和∠3是同旁内角 思考2两条平行线被第三条直线所截,同旁内角互补。平行的性质3:ab2134 3、整理归纳: 平行线的性质:
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补) 解:∵AD∥BC (已知)∴? A +? B=180°
∴ ∠B= 180°-? A=180°-115°=65°∵AD∥BC (已知) ∴? D+ ? C=180°∴? C=180°-? D =180°-100°=80°答:梯形的另外两个角分别为65°、80°. 例1 如图有一块梯形玻璃片的残余部分,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度。(两直线平行,同旁内角互补)(两直线平行,同旁内角互补)
1、如图,已知平行线AB、CD被直线AE所截;
(1)若∠1=110 °,则∠2=______.
(2)若∠1=110 °,则∠3=______.
(3)若∠1=110 °,则∠4=______.
2╭DB2、一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同,若测得第一次拐弯的∠B=142°,则第二次拐弯的∠C=_____°才合理?CB110°110°70°142°三、巩固练习:AD(1)DE和BC平行吗?为什么?
(2)∠C多少度?为什么?3、如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=80° 课本第21页 练习 T2同位角相等
内错角相等
同旁内角互补两直线平行判定性质四.谈收获:如图EF∥AD,∠1=∠2,∠BAC=70°,
(1) ∠2与∠3有什么数量关系?
(2)DG与BA是否平行,试说明理由。
(3)试求∠AGD的度数。拓展提高
现有一个梯形池塘,但有两个底角处都填满了土,只剩下两个完整的角,你能否设法求出该梯形池塘的四个角各是多少度吗?
5.3.1 平行线的性质二、协同探索:1、利用坐标纸上的直线,或者用直尺和三角尺,画出两条平行线a∥b,
2、画一条截线c,使之与直线a、b相交,
3、并找出一组同位角,标记为 ∠ 1 和∠ 2.
4、用量角器测量这一组同位角的大小,记录下来.从中你能发现什么?几何画板演示动动手!是不是任意一个三线八角图中,都有同位角相等呢?质疑:abc前提:被截线必须是平行线!两条平行线被第三条直线所截,同位角相等。ab21c平行的性质1:两直线平行,同位角相等。 如图,已知:a// b ,那么?3与?2有什么数量关系?
试说明理由! c如图:已知a//b,那么?2与? 4有什么数量关系呢?
试说明理由!思考1思考2小组讨论!动动脑!如图,已知:a// b ,那么?3与?2有什么关系? 答:∠ 2 = ∠3,理由如下:
因为 a∥b(已知),
所以 ∠1= ∠2( ),
因为∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等∠1思考1∠2和∠3是内错角 两条平行线被第三条直线所截,内错角相等。平行的性质2:cc如图:已知a//b,那么?2与? 4有什么关系呢????答: ? 2+ ? 4=180°,理由如下:
a//b (已知)
? 1= ? 2
(两直线平行,同位角相等)
? 1+ ? 4=180°
(邻补角定义)
? 2+ ? 4=180°
(等量代换)?∠2和∠3是同旁内角 思考2两条平行线被第三条直线所截,同旁内角互补。平行的性质3:ab2134 3、整理归纳: 平行线的性质:
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补) 解:∵AD∥BC (已知)∴? A +? B=180°
∴ ∠B= 180°-? A=180°-115°=65°∵AD∥BC (已知) ∴? D+ ? C=180°∴? C=180°-? D =180°-100°=80°答:梯形的另外两个角分别为65°、80°. 例1 如图有一块梯形玻璃片的残余部分,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度。(两直线平行,同旁内角互补)(两直线平行,同旁内角互补)
1、如图,已知平行线AB、CD被直线AE所截;
(1)若∠1=110 °,则∠2=______.
(2)若∠1=110 °,则∠3=______.
(3)若∠1=110 °,则∠4=______.
2╭DB2、一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同,若测得第一次拐弯的∠B=142°,则第二次拐弯的∠C=_____°才合理?CB110°110°70°142°三、巩固练习:AD(1)DE和BC平行吗?为什么?
(2)∠C多少度?为什么?3、如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=80° 课本第21页 练习 T2同位角相等
内错角相等
同旁内角互补两直线平行判定性质四.谈收获:如图EF∥AD,∠1=∠2,∠BAC=70°,
(1) ∠2与∠3有什么数量关系?
(2)DG与BA是否平行,试说明理由。
(3)试求∠AGD的度数。拓展提高
