沪科版八年级数学2024-2025学年八年级下册数学专项训练卷(三)(含答案)
文档属性
| 名称 | 沪科版八年级数学2024-2025学年八年级下册数学专项训练卷(三)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 22:30:25 | ||
图片预览



文档简介
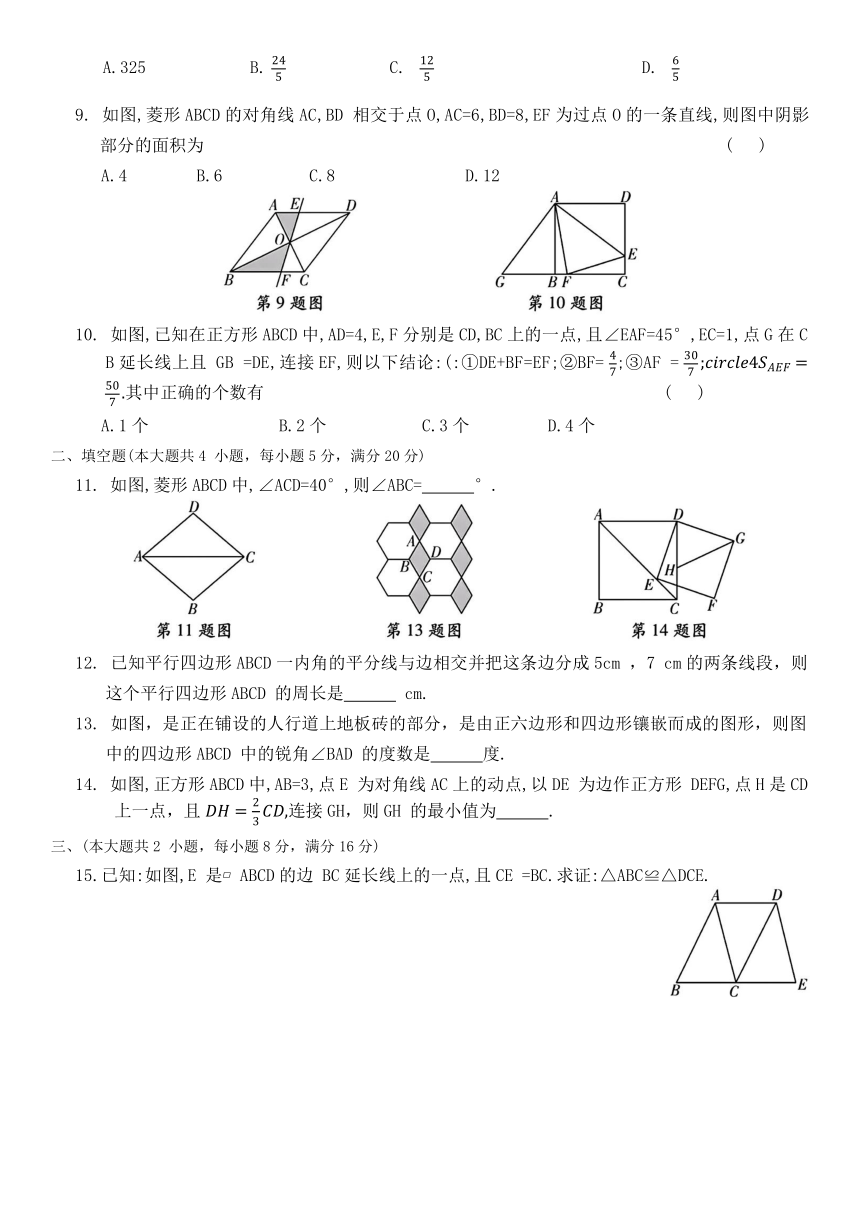
专项训练卷(三)
训练内容:四边形 时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 已知一个多边形的内角和是540°,则这个多边形的对角线条数是 ( )
A.5 B.7 C.9 D.10
2. 某中学新科技馆铺设地面,已有正方形地砖,现打算购买另一种正多边形地砖(边长与正方形的相等),与正方形地砖作平面镶嵌,则该学校可以购买的地砖形状是 ( )
A.正五边形 B.正六边形 C.正八边形 D.正十二边形
3. 在△ABC中,点D,E分别是△ABC 的边AB,AC的中点,连接DE.若∠C=68°,则∠AED =
( )
A.22° B.68° C.96° D.112°
4. 如图,五边形ABCDE中,AE∥CD,若∠A=∠C=110°,则∠B 的度数为 ( )
A.70°
B.110°
C.140°
D.150°
5. 在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论:①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.其中正确的有 ( )
A.①②③ B.①②④ C.②③④ D.①③④
6. 如图所示,在四边形ABCD中,∠BCD=90°,AB⊥BD于点 B,点E是BD的中点,连接AE,CE,则AE与CE 的大小关系是 ( )
A. AE=CE B. AE>CE C. AE7. 如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有 ( )
A.4个 B.5个 C.8个 D.9个
8. 如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OE⊥AC,交AD于点E,
过点 E作EF⊥BD,垂足为点 F,则OE+EF 的值为 ( )
A.325 B. C. D.
9. 如图,菱形ABCD的对角线AC,BD 相交于点O,AC=6,BD=8,EF为过点O的一条直线,则图中阴影部分的面积为 ( )
A.4 B.6 C.8 D.12
10. 如图,已知在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,点G在CB延长线上且 GB =DE,连接EF,则以下结论:(:①DE+BF=EF;②BF= ;③AF = 其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4 小题,每小题5分,满分20分)
11. 如图,菱形ABCD中,∠ACD=40°,则∠ABC= °.
12. 已知平行四边形ABCD一内角的平分线与边相交并把这条边分成5cm ,7 cm的两条线段,则这个平行四边形ABCD 的周长是 cm.
13. 如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD 中的锐角∠BAD 的度数是 度.
14. 如图,正方形ABCD中,AB=3,点E 为对角线AC上的动点,以DE 为边作正方形 DEFG,点H是CD 上一点,且 连接GH,则GH 的最小值为 .
三、(本大题共2 小题,每小题8分,满分16分)
15.已知:如图,E 是 ABCD的边 BC延长线上的一点,且CE =BC.求证:△ABC≌△DCE.
16. 已知:如图, ,点E,F分别是AC,BD的中点,求证:EF⊥BD.
四、(本大题共2小题,每小题8分,满分16分)
17. 一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形的边数.
(2)求这个多边形的内角和.
18. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM 为平行四边形.
(2)若AD=4,AB=2,且MN⊥AC,求DM的长.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:
(2)若 求菱形ABCD 的面积.
20. 如图,在正方形ABCD中,点E是BC上的一点,点F 是CD延长线上的一点,且 连接AE,AF,EF.
(1)求证:
(2)若 求EF的长.
六、(本题满分12分)
21. 在 中, 以 BC为边作周长为18 的矩形 BCDE,M,N分别为AC,CD的中点,连接MN.请你画出图形,并直接写出线段MN的长.
七、(本题满分12分)
22. 已知:在 中, ,点D,E分别是AB,AC的中点,连接DE 并延长交外角. 的平分线 CN于点 F.
(1)求证:
(2)连接CD,AF,当. 满足什么条件时,四边形ADCF 为正方形 请说明理由.
八、(本题满分14分)
23. 如图,D,E分别是 的边AB,AC上的点,把 沿DE折叠,使点A 落在四边形 BCED所在的平面上,点A 的对应点为 已知
(1)求 的度数.
(2)在图①,图②,图③中,写出. 的数量关系,并选择一种情况说明理由.
专项训练卷(三)
1. A 2. C 3. B 4. C 5. B 6. B 7. D 8. C 9. B 10. C11. 100 12. 34或3813. 60
15. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠B=∠DCE.在△ABC和△DCE中, ∴△ABC≌△DCE(SAS).
16. 证明:连接DE,BE,
∵ ∠ABC=∠ADC=90°,E为AC 的中点,
∴BE=DE,∵ F为BD的中点,
∴EF⊥BD.17. 解:(1)设多边形的每一个内角为x,则每一个外角为 由题意得 解得 这个多边形的边数为:
(2)由(1)知,该多边形是六边形,
∴内角和为(6-2)×180°=720°.
18. (1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,∴∠OAM=∠OCN,∠OMA=∠ONC.
在△AOM和△CON中,
∴ △AOM≌△CON(AAS),∴AM=CN.
∵AM∥CN,∴四边形ANCM为平行四边形.
(2)解:∵在矩形ABCD中,AD=BC,由(1)知AM=CN,
∴DM=BN.∵ 四边形ANCM 为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,∴AM=AN=NC=AD-DM.在 Rt△ABN中,根据勾股定理,得 即 解得
19. (1)证明:∵四边形ABCD是菱形,∴AB=AD.
∵点E,F分别是边AD,AB的中点,∴AF=AE.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS).
(2)解:连接BD,如图,
∵四边形ABCD 是菱形,
∴AB=AD,∠A=∠C=60°,
∴ △ABD 是等边三角形.
∵点E是边AD的中点,∴BE⊥AD,
在Rt△ABE中,设AE=x,则AB=2x,根据勾股定理,得 即 解得 (舍去), ∴AE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积为
20. (1)证明:∵ 四边形ABCD 是正方形,
∴AB=AD,∠ABC=∠ADC=∠ADF=90°,
在△ABE和△ADF中,
(2)解:∵△ABE≌△ADF,∴AE=AF,∠BAE=∠DAF,∵∠BAE+∠EAD =90°,∴∠DAF+∠EAD =90°,即∠EAF = (-
21. 解: 中BC边上的高为6×2÷6=2,而矩形 BCDE的周长为18,BC=6,∴BE=CD=18÷2-6=3.
①当矩形 BCDE 和△ABC在 BC同侧时,过点A作AF⊥BC,垂足为F,与ED交于点G,连接AD,如图1,
∵AB=AC,∴BF=CF=3.
∵ ∠GFC=∠FCD=∠CDG=90°,
∴ 四边形CFGD 是矩形,∴DG=CF=3,易知AF=2,∴AG=GF-AF=3-2=1,
∵M,N分别为AC和CD的中点,.
②当矩形 BCDE和. 在BC异侧时,过点A作. 垂足为F,与BC交于点G,连接AD,如图2,
易知 ,F为ED的中点,
∵M,N分别为AC和CD的中点,∴ 综上,MN的长为 求
22. (1)证明:
平分
∴ ∠A =∠ACF.∵E是AC的中点,.
在 与 中,
(2)解:当∠ACB=90°时,
四边形ADCF 是正方形.
理由如下:连接CD,AF,由(1)知∠A=∠ACF,可得AD∥CF,又知AD=CF,
∴ 四边形 ADCF 为平行四边形.
∵CB=CA,D为AB中点,∴CD⊥AB,
∴四边形ADCF 为矩形,当AC⊥BC,即∠ACB=90°时, 此时四边形ADCF 为正方形.
23. 解:(1)∵∠B=80°,∠C=70°,
∴∠A=180°-(∠B+∠C)=30°.
(2)数量关系分别为:∠1-∠2=2∠A,∠1 +∠2 =2∠A,∠2-∠1=2∠A,理由如下:
图①:如图,AC与A'D交于点 H,
∵ ∠AHD=∠A'+∠2,∠A'=∠A,
∴∠AHD=∠A+∠2.
∵∠1 =∠A+∠AHD,
∴∠1=∠A+∠A+∠2,
∴ ∠1--∠2=2∠A.
图②:由折叠可知,∠A=∠A',∠AED=∠A'ED,∠ADE = ∠A'DE.∵ ∠1 +2∠ADE = 180°,∠2 +2∠AED =180°,∴∠1+∠2+2(∠AED+∠ADE)=360°.
又∵∠A+∠AED+∠ADE=180°,∴∠AED+∠ADE =180°-
即
图③:如图,AB与. 交于点M,
训练内容:四边形 时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 已知一个多边形的内角和是540°,则这个多边形的对角线条数是 ( )
A.5 B.7 C.9 D.10
2. 某中学新科技馆铺设地面,已有正方形地砖,现打算购买另一种正多边形地砖(边长与正方形的相等),与正方形地砖作平面镶嵌,则该学校可以购买的地砖形状是 ( )
A.正五边形 B.正六边形 C.正八边形 D.正十二边形
3. 在△ABC中,点D,E分别是△ABC 的边AB,AC的中点,连接DE.若∠C=68°,则∠AED =
( )
A.22° B.68° C.96° D.112°
4. 如图,五边形ABCDE中,AE∥CD,若∠A=∠C=110°,则∠B 的度数为 ( )
A.70°
B.110°
C.140°
D.150°
5. 在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论:①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.其中正确的有 ( )
A.①②③ B.①②④ C.②③④ D.①③④
6. 如图所示,在四边形ABCD中,∠BCD=90°,AB⊥BD于点 B,点E是BD的中点,连接AE,CE,则AE与CE 的大小关系是 ( )
A. AE=CE B. AE>CE C. AE
A.4个 B.5个 C.8个 D.9个
8. 如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OE⊥AC,交AD于点E,
过点 E作EF⊥BD,垂足为点 F,则OE+EF 的值为 ( )
A.325 B. C. D.
9. 如图,菱形ABCD的对角线AC,BD 相交于点O,AC=6,BD=8,EF为过点O的一条直线,则图中阴影部分的面积为 ( )
A.4 B.6 C.8 D.12
10. 如图,已知在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,点G在CB延长线上且 GB =DE,连接EF,则以下结论:(:①DE+BF=EF;②BF= ;③AF = 其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4 小题,每小题5分,满分20分)
11. 如图,菱形ABCD中,∠ACD=40°,则∠ABC= °.
12. 已知平行四边形ABCD一内角的平分线与边相交并把这条边分成5cm ,7 cm的两条线段,则这个平行四边形ABCD 的周长是 cm.
13. 如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD 中的锐角∠BAD 的度数是 度.
14. 如图,正方形ABCD中,AB=3,点E 为对角线AC上的动点,以DE 为边作正方形 DEFG,点H是CD 上一点,且 连接GH,则GH 的最小值为 .
三、(本大题共2 小题,每小题8分,满分16分)
15.已知:如图,E 是 ABCD的边 BC延长线上的一点,且CE =BC.求证:△ABC≌△DCE.
16. 已知:如图, ,点E,F分别是AC,BD的中点,求证:EF⊥BD.
四、(本大题共2小题,每小题8分,满分16分)
17. 一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形的边数.
(2)求这个多边形的内角和.
18. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.
(1)求证:四边形ANCM 为平行四边形.
(2)若AD=4,AB=2,且MN⊥AC,求DM的长.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:
(2)若 求菱形ABCD 的面积.
20. 如图,在正方形ABCD中,点E是BC上的一点,点F 是CD延长线上的一点,且 连接AE,AF,EF.
(1)求证:
(2)若 求EF的长.
六、(本题满分12分)
21. 在 中, 以 BC为边作周长为18 的矩形 BCDE,M,N分别为AC,CD的中点,连接MN.请你画出图形,并直接写出线段MN的长.
七、(本题满分12分)
22. 已知:在 中, ,点D,E分别是AB,AC的中点,连接DE 并延长交外角. 的平分线 CN于点 F.
(1)求证:
(2)连接CD,AF,当. 满足什么条件时,四边形ADCF 为正方形 请说明理由.
八、(本题满分14分)
23. 如图,D,E分别是 的边AB,AC上的点,把 沿DE折叠,使点A 落在四边形 BCED所在的平面上,点A 的对应点为 已知
(1)求 的度数.
(2)在图①,图②,图③中,写出. 的数量关系,并选择一种情况说明理由.
专项训练卷(三)
1. A 2. C 3. B 4. C 5. B 6. B 7. D 8. C 9. B 10. C11. 100 12. 34或3813. 60
15. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠B=∠DCE.在△ABC和△DCE中, ∴△ABC≌△DCE(SAS).
16. 证明:连接DE,BE,
∵ ∠ABC=∠ADC=90°,E为AC 的中点,
∴BE=DE,∵ F为BD的中点,
∴EF⊥BD.17. 解:(1)设多边形的每一个内角为x,则每一个外角为 由题意得 解得 这个多边形的边数为:
(2)由(1)知,该多边形是六边形,
∴内角和为(6-2)×180°=720°.
18. (1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,∴∠OAM=∠OCN,∠OMA=∠ONC.
在△AOM和△CON中,
∴ △AOM≌△CON(AAS),∴AM=CN.
∵AM∥CN,∴四边形ANCM为平行四边形.
(2)解:∵在矩形ABCD中,AD=BC,由(1)知AM=CN,
∴DM=BN.∵ 四边形ANCM 为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,∴AM=AN=NC=AD-DM.在 Rt△ABN中,根据勾股定理,得 即 解得
19. (1)证明:∵四边形ABCD是菱形,∴AB=AD.
∵点E,F分别是边AD,AB的中点,∴AF=AE.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS).
(2)解:连接BD,如图,
∵四边形ABCD 是菱形,
∴AB=AD,∠A=∠C=60°,
∴ △ABD 是等边三角形.
∵点E是边AD的中点,∴BE⊥AD,
在Rt△ABE中,设AE=x,则AB=2x,根据勾股定理,得 即 解得 (舍去), ∴AE=1,AB=2AE=2,∴AD=AB=2,∴菱形ABCD的面积为
20. (1)证明:∵ 四边形ABCD 是正方形,
∴AB=AD,∠ABC=∠ADC=∠ADF=90°,
在△ABE和△ADF中,
(2)解:∵△ABE≌△ADF,∴AE=AF,∠BAE=∠DAF,∵∠BAE+∠EAD =90°,∴∠DAF+∠EAD =90°,即∠EAF = (-
21. 解: 中BC边上的高为6×2÷6=2,而矩形 BCDE的周长为18,BC=6,∴BE=CD=18÷2-6=3.
①当矩形 BCDE 和△ABC在 BC同侧时,过点A作AF⊥BC,垂足为F,与ED交于点G,连接AD,如图1,
∵AB=AC,∴BF=CF=3.
∵ ∠GFC=∠FCD=∠CDG=90°,
∴ 四边形CFGD 是矩形,∴DG=CF=3,易知AF=2,∴AG=GF-AF=3-2=1,
∵M,N分别为AC和CD的中点,.
②当矩形 BCDE和. 在BC异侧时,过点A作. 垂足为F,与BC交于点G,连接AD,如图2,
易知 ,F为ED的中点,
∵M,N分别为AC和CD的中点,∴ 综上,MN的长为 求
22. (1)证明:
平分
∴ ∠A =∠ACF.∵E是AC的中点,.
在 与 中,
(2)解:当∠ACB=90°时,
四边形ADCF 是正方形.
理由如下:连接CD,AF,由(1)知∠A=∠ACF,可得AD∥CF,又知AD=CF,
∴ 四边形 ADCF 为平行四边形.
∵CB=CA,D为AB中点,∴CD⊥AB,
∴四边形ADCF 为矩形,当AC⊥BC,即∠ACB=90°时, 此时四边形ADCF 为正方形.
23. 解:(1)∵∠B=80°,∠C=70°,
∴∠A=180°-(∠B+∠C)=30°.
(2)数量关系分别为:∠1-∠2=2∠A,∠1 +∠2 =2∠A,∠2-∠1=2∠A,理由如下:
图①:如图,AC与A'D交于点 H,
∵ ∠AHD=∠A'+∠2,∠A'=∠A,
∴∠AHD=∠A+∠2.
∵∠1 =∠A+∠AHD,
∴∠1=∠A+∠A+∠2,
∴ ∠1--∠2=2∠A.
图②:由折叠可知,∠A=∠A',∠AED=∠A'ED,∠ADE = ∠A'DE.∵ ∠1 +2∠ADE = 180°,∠2 +2∠AED =180°,∴∠1+∠2+2(∠AED+∠ADE)=360°.
又∵∠A+∠AED+∠ADE=180°,∴∠AED+∠ADE =180°-
即
图③:如图,AB与. 交于点M,
