2024年北京延庆高二(上)期中数学(PDF版,含答案)
文档属性
| 名称 | 2024年北京延庆高二(上)期中数学(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 09:48:51 | ||
图片预览




文档简介
2024 2025
本试卷共 6 页,150 分。考试时长 120 分钟。考生务必将答案答在答题纸上,在试
卷上作答无效。考试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共 40分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合
题目要求的一项。
(1)在复平面内,复数1 i 的共.轭.复.数.对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(2)已知向量 a ( 1,2,1),b (3, x, y)且 a // b,那么 | b | =
(A)3 6 (B) 6 (C)9 (D)18
(3)在空间直角坐标系中,点 P(1, 2,3)关于坐标平面 xOy 的对称点为
(A) (1, 2,3) (B) (1,2, 3) (C) (1, 2, 3) (D) ( 1,2,3)
(4)设 v1 (0,1,1) , v (1,0, 1) 分别是空间中直线 l1 , l2 2 的方向向量,则直线 l1 , l2 所
成角的大小为
5 2
(A) (B) (C) (D)
6 6 3 3
(5)过 ( 2, 0)和 (0, 2) 两点的直线的倾斜角是
3
(A) 1 (B)1 (C) (D)
4 4
(6)“ a 1”是“直线 l1 : ax y 2 0 与 l2 : 2x (a 1)y 2 0 平行”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
高二年级(数学) 第 1 页(共 6页)
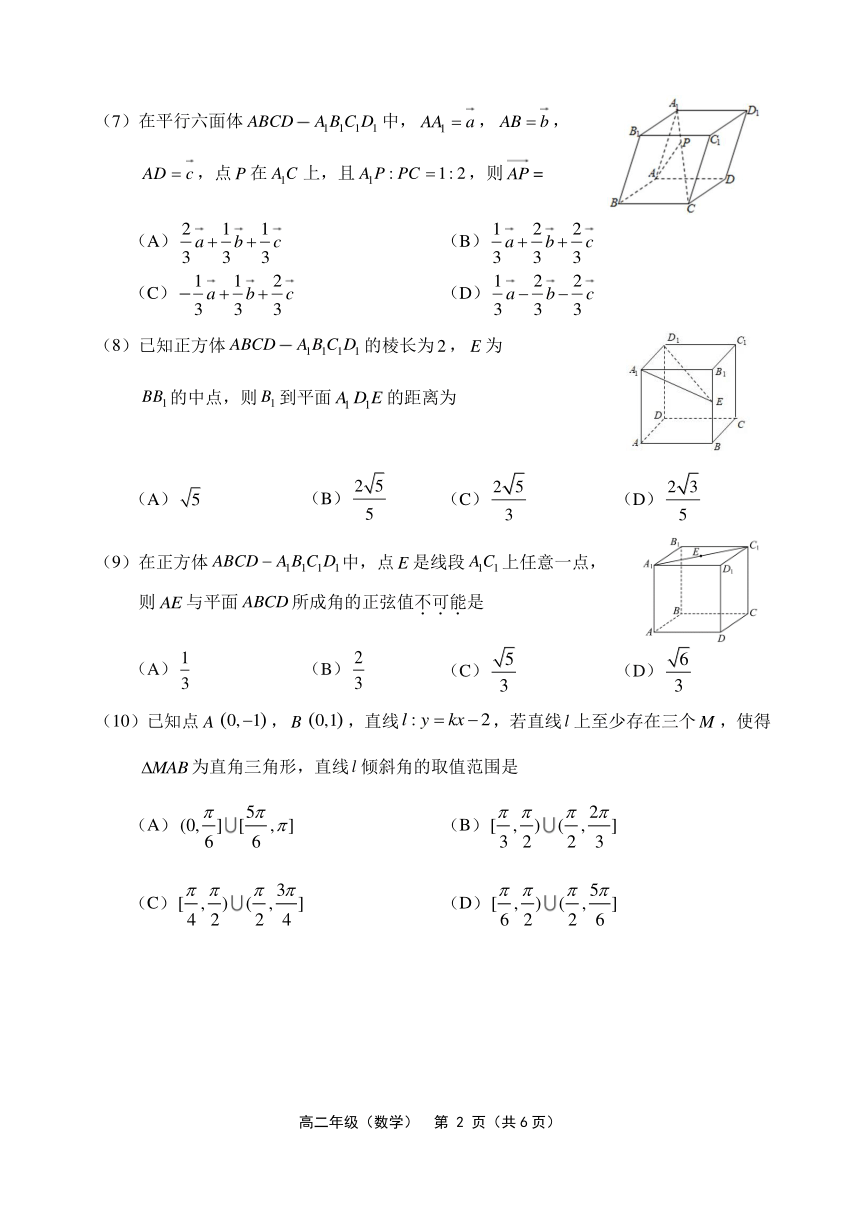
(7)在平行六面体 ABCD A1B1C1D1 中, AA1 a , AB b ,
AD c,点 P 在 A1C 上,且 A1P : PC 1: 2,则 AP =
2 1 1 1 2 2
(A) a b c (B) a b c
3 3 3 3 3 3
1 1 2 1 2 2
(C) a b c (D) a b c
3 3 3 3 3 3
(8)已知正方体 ABCD A1B1C1D1 的棱长为 2, E 为
BB1的中点,则 B1 到平面 A1 D1E 的距离为
2 5 2 5 2 3
(A) 5 (B) (C) (D)
5 3 5
(9)在正方体 ABCD A1B1C1D1中,点 E 是线段 A1C1上任意一点,
则 AE 与平面 ABCD所成角的正弦值不.可.能.是
1 2 5 6
(A) (B) (C) (D)
3 3 3 3
(10)已知点 A (0, 1) ,B (0,1) ,直线 l : y kx 2,若直线 l 上至少存在三个M ,使得
MAB为直角三角形,直线 l 倾斜角的取值范围是
5 2
(A) (0, ] [ , ] (B)[ , ) ( , ]
6 6 3 2 2 3
3 5
(C)[ , ) ( , ] (D)[ , ) ( , ]
4 2 2 4 6 2 2 6
高二年级(数学) 第 2 页(共 6页)
第二部分 (非选择题 共 110 分)
二、填空题共 5小题,每小题 5分,共 25 分。
5i
(11)复数 z ,则 | z | = .
1 2i
(12)已知点 A(1,1, 4), B(1, 4, 2) ,点C 在线段 AB 上,且 | AC | 2 | CB |,则点C 坐标
为 .
(13)若平面 ,平面 的法向量为 n1 (1, 2,3) ,平面 的法向量为 n2 (x, y, 0),
写出平面 的一个法向量 .
(14)已知点 A(1,3), B( 1,4),直线 l : y ax 2与线段 AB 无.交.点.,则直线 l 在
y 轴上
的截距为 ;a的取值范围是 .
(15)如图:在直三棱柱 ABC A1 B1 C1 中, AB BB 3 , BC 3 , ABC 90 ,1
CH xCB ,CP yCB1(0 x 1,0 y 1) .记 f (x, y) AH HP,给出下列四个
结论:
①存在H ,使得任意 P ,都有 AH HP;
②对于任意点H ,都不.存.在.点 P ,使得平面 AHP 平面 A1B1C ;
③ f (x, y)的最小值为3;
④当 f (x, y)取最小时,过点 A,H , P 作三棱柱的截面,则截面周长为5 6 .
其中,所有正确结论的序号是 .
高二年级(数学) 第 3 页(共 6页)
三、解答题共 6小题,共 85分。解答应写出文字说明,证明过程或演算步骤。
(16)(本小题 13 分)
已知△ABC 的顶点坐标为 A( 1,5) 、 B( 2, 1) 、C(4,3) .
(Ⅰ)求过点 B 且与直线 AC 平行的直线的方程;
(Ⅱ)求 BC 边上的中线所在直线的方程;
(Ⅲ)求 AB 边上的高所在直线的方程.
(17)(本小题 14 分)
如图,在三棱柱 ABC A1B1C1 中, CC1 底面 ABC , D 是 A1C1 的中点,且
AC BC CC1 2.
(Ⅰ)求证: BC1 // 平面 AB1D ;
(Ⅱ)若 AC BC ,求直线CC1与平面 AB1D 所成角的正
弦值;
(Ⅲ)若 AC BC ,求平面 AB1D 与平面 ACC1A1 所成角
的余弦值.
(18)(本小题 14 分)
设△ABC 的内角 A, B ,C 对应的边分别为 a ,b , c ,且b sin A 3a cos B .
(Ⅰ)求角 B 的大小;
(Ⅱ)从下列三个条件中选择一组作为已知,使△ABC 存.在.且.唯.一.,并求△ABC 的面积.
条件①:b 3, sinC 2sin A ;
条件②:b 21, a 5 ;
21
条件③:b 21, cosC .
7
注:如果选择的条件使△ABC 不存在或不唯一,第(Ⅱ)问得0 分.
高二年级(数学) 第 4 页(共 6页)
(19)(本小题 14 分)
2
已知函数 f (x) 2a sin x cos x 2 cos x,且 f (x)的图像过点 ( , 0) .
6
(Ⅰ)求函数 f (x)的最小正周期和单调递减区间;
(Ⅱ)若函数 f (x)在[ , m]上与直线 y 3有交点,求实数m 的取值范围;
12
11
(Ⅲ)设函数 g(x) | f (x) t | ( t R ),记函数 g(x)在[ , ] 上的最大值为M (t),
6 12
求M (t)的最小值及此时 t 的值.
(20)(本小题 15 分)
如图,已知四棱锥 P ABCD中,底面 ABCD 是边长为 4的正方形,CD 平面
PAD , PAD是正三角形, E , F ,G ,O 分别为 PC , PD, BC , AD 的中点.
(Ⅰ)求证: PO 平面 ABCD;
(Ⅱ)求点 A到平面 EFG 的距离;
(Ⅲ)线段 PC 上是否存在点M ,使得三棱锥M EFG
3 PM
的体积为 ,若存在,求 的值;若不存在,
3 PC
说明理由.
高二年级(数学) 第 5 页(共 6页)
(21)(本小题 15 分)
给定正整数 n 2 ,设集合M { | (t1,t2 , ,tn ),tk {0,1},k 1,2, ,n}.对于集
合M 中的任意元素 (x1, x2 , , xn )和 (y1, y2 , , yn ),记
x1y1 x2 y x y A M2 n n .设 ,且集合 A { i | i (ti1,ti2 , ,tin ),i 1,2, ,n},
p, i j,
对于 A中任意元素 i , j ,若 i j 则称 A具有性质T(n, p) .
1, i j,
(Ⅰ)判断集合 A {(1,1,0),(1,0,1),(0,1,1)}是否具有性质T (3,2),
集合B {(1,1,0,0),(1,0,1,0),(0,1,1,0),(1,0,0,1)}是否具有性质T(4,2);
(直接写出答案,结论不需要证明)
(Ⅱ)判断是否存在具有性质T(4, p) 的集合 A,并加以证明;
(Ⅲ)若集合 A具有性质T(n, p) ,证明: t1 j t2 j tnj p ( j 1,2, ,n) .
高二年级(数学) 第 6 页(共 6页)
延庆区 2024-2025学年第一学期期中考试
高二数学参考答案及评分标准 2024.11
一、选择题(共 10 小题,每小题 4 分,共 40 分)
(1)D (2)A (3)B (4)C (5)D
(6)C (7)A (8)B (9)A (10)B
二、填空题(共 5 小题,每小题 5 分,共 25 分)
(11) 5 (12) (1,3,0) (13) (2, 1,0) (不唯一,共线即可)
(14) 2, ( 6,5) (注: 第一问 3 分,第二问 2 分)
(15)①③④ (注:对一个 2 分,两个 3 分,有选错 0 分)
三、解答题(共 6 小题,共 85 分)
(16)(共 13 分)
5 3 2
解:(Ⅰ)直线 AC 的斜率 kAC = = ……2 分
1 4 5
2
过点 B 且与直线 AC 平行的直线的斜率为 ……4 分
5
过点 B 且与直线 AC 平行的直线方程为
2
y +1= (x + 2) 2x +5y +9 = 0 ……5 分
5
(Ⅱ)设 BC 边的中点为D ,因为 B ( 2, 1)、C (4,3),
2+ 4 1+3
所以点D 的坐标为 , ,即 D (1,1), ……7 分
2 2
5 1
kAD = = 2 ……8 分
1 1
所以 BC 边的中线所在直线方程为 y 1= 2(x 1) 2x + y 3 = 0 ……9 分
1 5
(Ⅲ)因为 kAB = = 6 , ……10 分
2 +1
1
所以 AB 边的高线所在直线的斜率为 , ……12 分
6
高二数学答案 第 1 页(共 7 页)
1
因此 AB 边的高线所在直线方程为 y 3 = (x 4) x + 6y 22 = 0 .……13 分
6
(17)(共 14 分)
(Ⅰ)证明:连接 A1B,设 A1B∩AB1=E,连接 DE,
由 ABC﹣A1B1C1 为三棱柱,得 A1E=BE.
又∵D 是 A1C1 的中点,所以 DE 是 A1BC1的中位线, ……1 分
∴BC1∥DE. ……2 分
∵BC1 平面 AB1D,DE 平面 AB1D, ……3 分
∴BC1∥平面 AB1D; ……4 分
(Ⅱ)解:∵CC1⊥底面 ABC,AC⊥BC, ……5 分
以 C 为原点,CA ,CB ,CC1 的方向分别为 x,y,z 轴正方向建立如图所示的空
间直角坐标系,则 C(0,0,0),A(2,0,0),B(0,2,0),
A1(2,0,2),B1(0,2,2),C1(0,0,2),D(1,0,2),
CC1 = (0, 0, 2) , AB1 = ( 2, 2, 2) , AD = ( 1, 0, 2)
设平面 AB1D 的法向量为 n = (x, y, z)
n AB1 = 2x + 2y + 2z = 0
由 ,得 n = (2,1,1) ; ……7 分
n AD = 2x + 2z = 0
高二数学答案 第 2 页(共 7 页)
设直线 C C1 与平面 AB1D 所成角为 θ.
n CC 6
则 sin =| cos n,CC 11 |= = . ……9 分
| n || CC | 61
6
∴直线 C C1 与平面 AB1D 所成角的正弦值为 . ……10 分
6
(Ⅲ)设平面 AB1D 与平面 ACC1A1所成角为 , 为锐角,
平面 ACC1A1的法向量为m = (0,1, 0) , ……11 分
n m 6
cos =| cos n, m |= = , ……13 分
| n || m | 6
6
平面 AB1D 与平面 ACC1A1所成角余弦值为 . ……14 分
6
(18)(共 14 分)
a b
解:(Ⅰ)∵b sin A = 3a cos B ,由正弦定理 = ……2 分
sin A sin B
得 sin B sin A = 3 sin Acos B , ……3 分
在△ABC 中,sinA≠0, tan B = 3 , ……4分
∵B∈(0,π), ……5 分
∴ B = . ……6 分
3
(Ⅱ)若选①,∵sinC=2sinA,c = 2a ……7 分
由余弦定理 b2
2 2 2
=a2+c2﹣2accosB,得9 = a + 4a 4a cos B , ……9 分
解得 a = 3 , c = 2 3 ……11 分
1 3 3
∴ S = acsin B = . ……14 分
2 2
21
若选③,∵ b = 21, cosC =
7
高二数学答案 第 3 页(共 7 页)
5 7
sin A = sin(B +C) = sin BcosC + cos BsinC = ……10 分
14
由正弦定理可得: c = 4 ……11 分
1
S = bcsin A = 5 3 ……14 分
2
选择②,面积公式 2 分;余弦定理 2 分.不超过 4 分.
(19)(共 14 分)
3 3
解:(Ⅰ)由题意, f = asin + 2cos
2
= a + 2 = 0 ,
6 3 6 2 4
解得 a = 3 . ……1 分
∴ f (x) = 3 sin 2x + 2cos2 x , ……2 分
= 3 sin 2x + cos 2x +1, ……3 分
= 2sin 2x + +1, ……4 分
6
2
f ( x)的最小正周期T = = ; ……5 分
2
2
f ( x)的单调减区间为[ + k , + k ],k z ……7 分
6 3
(Ⅱ)∵函数 f ( x)在区间 ,m 上与直线 y = 3有交点
12
所以,函数 f ( x)在区间 ,m 上的最大值为 3, ……8 分
12
又因为 2x + [0,2m+ ] ……9 分
6 6
所以 2m+ ,解得m . ……10 分
6 2 6
∴实数 m 的取值范围是 ,+ .
6
高二数学答案 第 4 页(共 7 页)
11
(Ⅲ) g(x) =| f (x) t |=| 2sin 2x + +1 t |, x [ , ], 2x + [ , 2 ]
6 6 12 6 2
当 2x + = 时, f (x) t 取最大值3 t
6 2
3
当2x + = 时, f (x) t 取最小值 1 t
6 2
所以,当 t 1时, M (t) = 3 t ……11分
当 t 1时, M (t) = t +1 ……12分
所以,当 t = 1时, M (t)min = 2 ……14分
(20)(共 15 分)
(Ⅰ)证明:因为△PAD 是正三角形,O 是 AD 的中点,
所以 PO⊥AD. ……1 分
又因为 CD⊥平面 PAD,PO 平面 PAD,CD⊥PO, ……2 分
AD∩CD=D,CD,AD 平面 ABCD, ……3 分
所以 PO⊥面 ABCD; ……4 分
解:(Ⅱ)因为OA,OG ,OP 两两互相垂直.以 O 点为原点,OA,OG ,OP 的方
向分别为 x,y,z 轴正方向建立如图所示的空间直角坐标系. ……5分
则O(0, 0, 0) , A(2, 0, 0), B(2, 4, 0),C( 2, 4, 0) , D( 2, 0, 0), P(0, 0, 2 3) ,
E( 1, 2, 3) , F ( 1, 0, 3) , G(0, 4, 0) ,
EF = (0, 2,0) , EG = (1, 2, 3) , FG = (1, 4, 3) .
高二数学答案 第 5 页(共 7 页)
设平面 EFG 的法向量为 n = (x, y, z) ,
n EF = 2y = 0
由 ,得 n = ( 3, 0,1) ……7 分
n EG = x + 2y 3z = 0
AE = ( 3, 2, 3) ,
| AE n |
点 A到平面 EFG 的距离d = = 3 ……9 分
| n |
1 1
(Ⅲ)设 PM = PC , [0, ) ( ,1] ……10 分
2 2
M ( 2 , 4 , 2 3 2 3 ) , EM = (1 2 , 4 2, 3 2 3 )
| PF n |
所以点 M 到面 EFG 的距离为定值 d = = 3 |1 2 | ……11 分
| n |
EF EG 4 2
cos EF , EG = = =
| EF || EG | 2 2 2 2
1
S EFG = | EF || EG | sin EF ,EG = 2 ……12 分
2
1 1 3
VM EFG = S EFGh = | EF || EG | sin EF ,EG h = , ……13 分
3 6 3
PM 1 3
解得: = = 或 . ……15 分
PC 4 4
(21)(共 15 分)
(Ⅰ)集合 A具有性质T (3,2), ……2 分
集合 B 不具有性质T (4,2) . ……4 分
(Ⅱ)当 n = 4 时,集合A 中的元素个数为 4 .由题设 p {0,1,2,3,4}.……5 分
假设集合A 具有性质T (4, p) ,则
①当 p = 0时, A = {(0,0,0,0)},矛盾.
②当 p =1时,A = {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)},不具有性质T (4,1) ,矛盾.
高二数学答案 第 6 页(共 7 页)
③当 p = 2 时, A {(1,1,0,0), (1,0,1,0), (1,0,0,1), (0,1,1,0), (0,1,0,1), (0,0,1,1)}.
因为 (1,1,0,0)和 (0,0,1,1)至多一个在A 中;(1,0,1,0)和 (0,1,0,1)至多一个在A 中;
(1,0,0,1)和 (0,1,1,0)至多一个在A 中,故集合A 中的元素个数小于 4 ,矛盾.
④当 p = 3时, A = {(1,1,1,0), (1,1,0,1), (1,0,1,1), (0,1,1,1)},不具有性质T (4,3),矛盾.
⑤当 p = 4 时, A = {(1,1,1,1)},矛盾.
综上,不存在具有性质T (4, p) 的集合A . ……10 分
(Ⅲ)记 c j = t1 j + t2 j + + tnj ( j =1,2, ,n) ,则 c1 + c2 + + cn = np .
若 p = 0,则 A = {(0,0, ,0)},矛盾.若 p =1,则 A = {(1,0,0, ,0)},矛盾.
故 p 2. ……11 分
假设存在 j 使得 c j ≥ p +1,不妨设 j =1,即 c1 ≥ p +1.
当 c1 = n时,有 c j = 0或 c j =1 ( j = 2,3, ,n) 成立.
所以 , , , 中分量为1的个数至多有 n + (n 1) = 2n 1 2n ≤ np1 2 n . ……12 分
当 p +1≤ c1 n时,不妨设 t11 = t21 = = t p+1,1 =1,tn1 = 0.
因为 n n = p ,所以 n 的各分量有 p 个1,不妨设 tn2 = tn3 = = tn, p+1 =1.
由 i j 时, i j =1可知, q {2,3, , p +1}, t1q , t2q , , t p+1,q 中至多有1个1,
即 1, 2 , , p+1 的前 p +1个分量中,至多含有 p +1+ p = 2 p +1个1. ……13 分
又 i =1 (i =1,2, , p +1),则 1, 2 , , n p+1 的前 p +1个分量中,含有
( p +1) + ( p +1) = 2 p + 2 个1,矛盾. ……14 分
所以 c j ≤ p ( j =1,2, ,n) . 因为 c1 + c2 + + cn = np ,
所以 c j = p ( j =1,2, ,n) .所以 t1 j + t2 j + + tnj = p ( j =1,2, ,n) .……15 分
高二数学答案 第 7 页(共 7 页)
本试卷共 6 页,150 分。考试时长 120 分钟。考生务必将答案答在答题纸上,在试
卷上作答无效。考试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共 40分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合
题目要求的一项。
(1)在复平面内,复数1 i 的共.轭.复.数.对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(2)已知向量 a ( 1,2,1),b (3, x, y)且 a // b,那么 | b | =
(A)3 6 (B) 6 (C)9 (D)18
(3)在空间直角坐标系中,点 P(1, 2,3)关于坐标平面 xOy 的对称点为
(A) (1, 2,3) (B) (1,2, 3) (C) (1, 2, 3) (D) ( 1,2,3)
(4)设 v1 (0,1,1) , v (1,0, 1) 分别是空间中直线 l1 , l2 2 的方向向量,则直线 l1 , l2 所
成角的大小为
5 2
(A) (B) (C) (D)
6 6 3 3
(5)过 ( 2, 0)和 (0, 2) 两点的直线的倾斜角是
3
(A) 1 (B)1 (C) (D)
4 4
(6)“ a 1”是“直线 l1 : ax y 2 0 与 l2 : 2x (a 1)y 2 0 平行”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
高二年级(数学) 第 1 页(共 6页)
(7)在平行六面体 ABCD A1B1C1D1 中, AA1 a , AB b ,
AD c,点 P 在 A1C 上,且 A1P : PC 1: 2,则 AP =
2 1 1 1 2 2
(A) a b c (B) a b c
3 3 3 3 3 3
1 1 2 1 2 2
(C) a b c (D) a b c
3 3 3 3 3 3
(8)已知正方体 ABCD A1B1C1D1 的棱长为 2, E 为
BB1的中点,则 B1 到平面 A1 D1E 的距离为
2 5 2 5 2 3
(A) 5 (B) (C) (D)
5 3 5
(9)在正方体 ABCD A1B1C1D1中,点 E 是线段 A1C1上任意一点,
则 AE 与平面 ABCD所成角的正弦值不.可.能.是
1 2 5 6
(A) (B) (C) (D)
3 3 3 3
(10)已知点 A (0, 1) ,B (0,1) ,直线 l : y kx 2,若直线 l 上至少存在三个M ,使得
MAB为直角三角形,直线 l 倾斜角的取值范围是
5 2
(A) (0, ] [ , ] (B)[ , ) ( , ]
6 6 3 2 2 3
3 5
(C)[ , ) ( , ] (D)[ , ) ( , ]
4 2 2 4 6 2 2 6
高二年级(数学) 第 2 页(共 6页)
第二部分 (非选择题 共 110 分)
二、填空题共 5小题,每小题 5分,共 25 分。
5i
(11)复数 z ,则 | z | = .
1 2i
(12)已知点 A(1,1, 4), B(1, 4, 2) ,点C 在线段 AB 上,且 | AC | 2 | CB |,则点C 坐标
为 .
(13)若平面 ,平面 的法向量为 n1 (1, 2,3) ,平面 的法向量为 n2 (x, y, 0),
写出平面 的一个法向量 .
(14)已知点 A(1,3), B( 1,4),直线 l : y ax 2与线段 AB 无.交.点.,则直线 l 在
y 轴上
的截距为 ;a的取值范围是 .
(15)如图:在直三棱柱 ABC A1 B1 C1 中, AB BB 3 , BC 3 , ABC 90 ,1
CH xCB ,CP yCB1(0 x 1,0 y 1) .记 f (x, y) AH HP,给出下列四个
结论:
①存在H ,使得任意 P ,都有 AH HP;
②对于任意点H ,都不.存.在.点 P ,使得平面 AHP 平面 A1B1C ;
③ f (x, y)的最小值为3;
④当 f (x, y)取最小时,过点 A,H , P 作三棱柱的截面,则截面周长为5 6 .
其中,所有正确结论的序号是 .
高二年级(数学) 第 3 页(共 6页)
三、解答题共 6小题,共 85分。解答应写出文字说明,证明过程或演算步骤。
(16)(本小题 13 分)
已知△ABC 的顶点坐标为 A( 1,5) 、 B( 2, 1) 、C(4,3) .
(Ⅰ)求过点 B 且与直线 AC 平行的直线的方程;
(Ⅱ)求 BC 边上的中线所在直线的方程;
(Ⅲ)求 AB 边上的高所在直线的方程.
(17)(本小题 14 分)
如图,在三棱柱 ABC A1B1C1 中, CC1 底面 ABC , D 是 A1C1 的中点,且
AC BC CC1 2.
(Ⅰ)求证: BC1 // 平面 AB1D ;
(Ⅱ)若 AC BC ,求直线CC1与平面 AB1D 所成角的正
弦值;
(Ⅲ)若 AC BC ,求平面 AB1D 与平面 ACC1A1 所成角
的余弦值.
(18)(本小题 14 分)
设△ABC 的内角 A, B ,C 对应的边分别为 a ,b , c ,且b sin A 3a cos B .
(Ⅰ)求角 B 的大小;
(Ⅱ)从下列三个条件中选择一组作为已知,使△ABC 存.在.且.唯.一.,并求△ABC 的面积.
条件①:b 3, sinC 2sin A ;
条件②:b 21, a 5 ;
21
条件③:b 21, cosC .
7
注:如果选择的条件使△ABC 不存在或不唯一,第(Ⅱ)问得0 分.
高二年级(数学) 第 4 页(共 6页)
(19)(本小题 14 分)
2
已知函数 f (x) 2a sin x cos x 2 cos x,且 f (x)的图像过点 ( , 0) .
6
(Ⅰ)求函数 f (x)的最小正周期和单调递减区间;
(Ⅱ)若函数 f (x)在[ , m]上与直线 y 3有交点,求实数m 的取值范围;
12
11
(Ⅲ)设函数 g(x) | f (x) t | ( t R ),记函数 g(x)在[ , ] 上的最大值为M (t),
6 12
求M (t)的最小值及此时 t 的值.
(20)(本小题 15 分)
如图,已知四棱锥 P ABCD中,底面 ABCD 是边长为 4的正方形,CD 平面
PAD , PAD是正三角形, E , F ,G ,O 分别为 PC , PD, BC , AD 的中点.
(Ⅰ)求证: PO 平面 ABCD;
(Ⅱ)求点 A到平面 EFG 的距离;
(Ⅲ)线段 PC 上是否存在点M ,使得三棱锥M EFG
3 PM
的体积为 ,若存在,求 的值;若不存在,
3 PC
说明理由.
高二年级(数学) 第 5 页(共 6页)
(21)(本小题 15 分)
给定正整数 n 2 ,设集合M { | (t1,t2 , ,tn ),tk {0,1},k 1,2, ,n}.对于集
合M 中的任意元素 (x1, x2 , , xn )和 (y1, y2 , , yn ),记
x1y1 x2 y x y A M2 n n .设 ,且集合 A { i | i (ti1,ti2 , ,tin ),i 1,2, ,n},
p, i j,
对于 A中任意元素 i , j ,若 i j 则称 A具有性质T(n, p) .
1, i j,
(Ⅰ)判断集合 A {(1,1,0),(1,0,1),(0,1,1)}是否具有性质T (3,2),
集合B {(1,1,0,0),(1,0,1,0),(0,1,1,0),(1,0,0,1)}是否具有性质T(4,2);
(直接写出答案,结论不需要证明)
(Ⅱ)判断是否存在具有性质T(4, p) 的集合 A,并加以证明;
(Ⅲ)若集合 A具有性质T(n, p) ,证明: t1 j t2 j tnj p ( j 1,2, ,n) .
高二年级(数学) 第 6 页(共 6页)
延庆区 2024-2025学年第一学期期中考试
高二数学参考答案及评分标准 2024.11
一、选择题(共 10 小题,每小题 4 分,共 40 分)
(1)D (2)A (3)B (4)C (5)D
(6)C (7)A (8)B (9)A (10)B
二、填空题(共 5 小题,每小题 5 分,共 25 分)
(11) 5 (12) (1,3,0) (13) (2, 1,0) (不唯一,共线即可)
(14) 2, ( 6,5) (注: 第一问 3 分,第二问 2 分)
(15)①③④ (注:对一个 2 分,两个 3 分,有选错 0 分)
三、解答题(共 6 小题,共 85 分)
(16)(共 13 分)
5 3 2
解:(Ⅰ)直线 AC 的斜率 kAC = = ……2 分
1 4 5
2
过点 B 且与直线 AC 平行的直线的斜率为 ……4 分
5
过点 B 且与直线 AC 平行的直线方程为
2
y +1= (x + 2) 2x +5y +9 = 0 ……5 分
5
(Ⅱ)设 BC 边的中点为D ,因为 B ( 2, 1)、C (4,3),
2+ 4 1+3
所以点D 的坐标为 , ,即 D (1,1), ……7 分
2 2
5 1
kAD = = 2 ……8 分
1 1
所以 BC 边的中线所在直线方程为 y 1= 2(x 1) 2x + y 3 = 0 ……9 分
1 5
(Ⅲ)因为 kAB = = 6 , ……10 分
2 +1
1
所以 AB 边的高线所在直线的斜率为 , ……12 分
6
高二数学答案 第 1 页(共 7 页)
1
因此 AB 边的高线所在直线方程为 y 3 = (x 4) x + 6y 22 = 0 .……13 分
6
(17)(共 14 分)
(Ⅰ)证明:连接 A1B,设 A1B∩AB1=E,连接 DE,
由 ABC﹣A1B1C1 为三棱柱,得 A1E=BE.
又∵D 是 A1C1 的中点,所以 DE 是 A1BC1的中位线, ……1 分
∴BC1∥DE. ……2 分
∵BC1 平面 AB1D,DE 平面 AB1D, ……3 分
∴BC1∥平面 AB1D; ……4 分
(Ⅱ)解:∵CC1⊥底面 ABC,AC⊥BC, ……5 分
以 C 为原点,CA ,CB ,CC1 的方向分别为 x,y,z 轴正方向建立如图所示的空
间直角坐标系,则 C(0,0,0),A(2,0,0),B(0,2,0),
A1(2,0,2),B1(0,2,2),C1(0,0,2),D(1,0,2),
CC1 = (0, 0, 2) , AB1 = ( 2, 2, 2) , AD = ( 1, 0, 2)
设平面 AB1D 的法向量为 n = (x, y, z)
n AB1 = 2x + 2y + 2z = 0
由 ,得 n = (2,1,1) ; ……7 分
n AD = 2x + 2z = 0
高二数学答案 第 2 页(共 7 页)
设直线 C C1 与平面 AB1D 所成角为 θ.
n CC 6
则 sin =| cos n,CC 11 |= = . ……9 分
| n || CC | 61
6
∴直线 C C1 与平面 AB1D 所成角的正弦值为 . ……10 分
6
(Ⅲ)设平面 AB1D 与平面 ACC1A1所成角为 , 为锐角,
平面 ACC1A1的法向量为m = (0,1, 0) , ……11 分
n m 6
cos =| cos n, m |= = , ……13 分
| n || m | 6
6
平面 AB1D 与平面 ACC1A1所成角余弦值为 . ……14 分
6
(18)(共 14 分)
a b
解:(Ⅰ)∵b sin A = 3a cos B ,由正弦定理 = ……2 分
sin A sin B
得 sin B sin A = 3 sin Acos B , ……3 分
在△ABC 中,sinA≠0, tan B = 3 , ……4分
∵B∈(0,π), ……5 分
∴ B = . ……6 分
3
(Ⅱ)若选①,∵sinC=2sinA,c = 2a ……7 分
由余弦定理 b2
2 2 2
=a2+c2﹣2accosB,得9 = a + 4a 4a cos B , ……9 分
解得 a = 3 , c = 2 3 ……11 分
1 3 3
∴ S = acsin B = . ……14 分
2 2
21
若选③,∵ b = 21, cosC =
7
高二数学答案 第 3 页(共 7 页)
5 7
sin A = sin(B +C) = sin BcosC + cos BsinC = ……10 分
14
由正弦定理可得: c = 4 ……11 分
1
S = bcsin A = 5 3 ……14 分
2
选择②,面积公式 2 分;余弦定理 2 分.不超过 4 分.
(19)(共 14 分)
3 3
解:(Ⅰ)由题意, f = asin + 2cos
2
= a + 2 = 0 ,
6 3 6 2 4
解得 a = 3 . ……1 分
∴ f (x) = 3 sin 2x + 2cos2 x , ……2 分
= 3 sin 2x + cos 2x +1, ……3 分
= 2sin 2x + +1, ……4 分
6
2
f ( x)的最小正周期T = = ; ……5 分
2
2
f ( x)的单调减区间为[ + k , + k ],k z ……7 分
6 3
(Ⅱ)∵函数 f ( x)在区间 ,m 上与直线 y = 3有交点
12
所以,函数 f ( x)在区间 ,m 上的最大值为 3, ……8 分
12
又因为 2x + [0,2m+ ] ……9 分
6 6
所以 2m+ ,解得m . ……10 分
6 2 6
∴实数 m 的取值范围是 ,+ .
6
高二数学答案 第 4 页(共 7 页)
11
(Ⅲ) g(x) =| f (x) t |=| 2sin 2x + +1 t |, x [ , ], 2x + [ , 2 ]
6 6 12 6 2
当 2x + = 时, f (x) t 取最大值3 t
6 2
3
当2x + = 时, f (x) t 取最小值 1 t
6 2
所以,当 t 1时, M (t) = 3 t ……11分
当 t 1时, M (t) = t +1 ……12分
所以,当 t = 1时, M (t)min = 2 ……14分
(20)(共 15 分)
(Ⅰ)证明:因为△PAD 是正三角形,O 是 AD 的中点,
所以 PO⊥AD. ……1 分
又因为 CD⊥平面 PAD,PO 平面 PAD,CD⊥PO, ……2 分
AD∩CD=D,CD,AD 平面 ABCD, ……3 分
所以 PO⊥面 ABCD; ……4 分
解:(Ⅱ)因为OA,OG ,OP 两两互相垂直.以 O 点为原点,OA,OG ,OP 的方
向分别为 x,y,z 轴正方向建立如图所示的空间直角坐标系. ……5分
则O(0, 0, 0) , A(2, 0, 0), B(2, 4, 0),C( 2, 4, 0) , D( 2, 0, 0), P(0, 0, 2 3) ,
E( 1, 2, 3) , F ( 1, 0, 3) , G(0, 4, 0) ,
EF = (0, 2,0) , EG = (1, 2, 3) , FG = (1, 4, 3) .
高二数学答案 第 5 页(共 7 页)
设平面 EFG 的法向量为 n = (x, y, z) ,
n EF = 2y = 0
由 ,得 n = ( 3, 0,1) ……7 分
n EG = x + 2y 3z = 0
AE = ( 3, 2, 3) ,
| AE n |
点 A到平面 EFG 的距离d = = 3 ……9 分
| n |
1 1
(Ⅲ)设 PM = PC , [0, ) ( ,1] ……10 分
2 2
M ( 2 , 4 , 2 3 2 3 ) , EM = (1 2 , 4 2, 3 2 3 )
| PF n |
所以点 M 到面 EFG 的距离为定值 d = = 3 |1 2 | ……11 分
| n |
EF EG 4 2
cos EF , EG = = =
| EF || EG | 2 2 2 2
1
S EFG = | EF || EG | sin EF ,EG = 2 ……12 分
2
1 1 3
VM EFG = S EFGh = | EF || EG | sin EF ,EG h = , ……13 分
3 6 3
PM 1 3
解得: = = 或 . ……15 分
PC 4 4
(21)(共 15 分)
(Ⅰ)集合 A具有性质T (3,2), ……2 分
集合 B 不具有性质T (4,2) . ……4 分
(Ⅱ)当 n = 4 时,集合A 中的元素个数为 4 .由题设 p {0,1,2,3,4}.……5 分
假设集合A 具有性质T (4, p) ,则
①当 p = 0时, A = {(0,0,0,0)},矛盾.
②当 p =1时,A = {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)},不具有性质T (4,1) ,矛盾.
高二数学答案 第 6 页(共 7 页)
③当 p = 2 时, A {(1,1,0,0), (1,0,1,0), (1,0,0,1), (0,1,1,0), (0,1,0,1), (0,0,1,1)}.
因为 (1,1,0,0)和 (0,0,1,1)至多一个在A 中;(1,0,1,0)和 (0,1,0,1)至多一个在A 中;
(1,0,0,1)和 (0,1,1,0)至多一个在A 中,故集合A 中的元素个数小于 4 ,矛盾.
④当 p = 3时, A = {(1,1,1,0), (1,1,0,1), (1,0,1,1), (0,1,1,1)},不具有性质T (4,3),矛盾.
⑤当 p = 4 时, A = {(1,1,1,1)},矛盾.
综上,不存在具有性质T (4, p) 的集合A . ……10 分
(Ⅲ)记 c j = t1 j + t2 j + + tnj ( j =1,2, ,n) ,则 c1 + c2 + + cn = np .
若 p = 0,则 A = {(0,0, ,0)},矛盾.若 p =1,则 A = {(1,0,0, ,0)},矛盾.
故 p 2. ……11 分
假设存在 j 使得 c j ≥ p +1,不妨设 j =1,即 c1 ≥ p +1.
当 c1 = n时,有 c j = 0或 c j =1 ( j = 2,3, ,n) 成立.
所以 , , , 中分量为1的个数至多有 n + (n 1) = 2n 1 2n ≤ np1 2 n . ……12 分
当 p +1≤ c1 n时,不妨设 t11 = t21 = = t p+1,1 =1,tn1 = 0.
因为 n n = p ,所以 n 的各分量有 p 个1,不妨设 tn2 = tn3 = = tn, p+1 =1.
由 i j 时, i j =1可知, q {2,3, , p +1}, t1q , t2q , , t p+1,q 中至多有1个1,
即 1, 2 , , p+1 的前 p +1个分量中,至多含有 p +1+ p = 2 p +1个1. ……13 分
又 i =1 (i =1,2, , p +1),则 1, 2 , , n p+1 的前 p +1个分量中,含有
( p +1) + ( p +1) = 2 p + 2 个1,矛盾. ……14 分
所以 c j ≤ p ( j =1,2, ,n) . 因为 c1 + c2 + + cn = np ,
所以 c j = p ( j =1,2, ,n) .所以 t1 j + t2 j + + tnj = p ( j =1,2, ,n) .……15 分
高二数学答案 第 7 页(共 7 页)
同课章节目录
