1.1---1.2 全等图形、全等三角形 同步练习(含答案)2024-2025学年苏科版数学八年级上册
文档属性
| 名称 | 1.1---1.2 全等图形、全等三角形 同步练习(含答案)2024-2025学年苏科版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 14:04:30 | ||
图片预览

文档简介
八年级上学期 · 第1章1.1&1.2单元同步练习卷
教材版本 苏科版 练习时间 90分钟 练习难度 ★★★☆☆
练习范围 主要对1.1全等图形, 1.2全等三角形相关知识进行练习
一、 选择题 (本大题共8小题, 每小题2分, 共计16分。 )
1. 下列说法错误的是( ) .
A. 如果两个图形全等,那么它们的形状和大小一定相同
B. 全等三角形的对应边相等,对应角相等
C. 图形全等,只与形状、大小有关,而与它们的位置无关
D. 面积相等的两个图形是全等图形
2. 下列图形:①两个正方形;②底边相等的两个等腰三角形;③每边都是2cm的两个三角
形;④半径都是1.5cm的两个圆 .其中是一对全等图形的有( ) .
A. 1个 B. 2个 C. 3个 D. 4个
3. 下列说法正确的是( ) .
A. 全等三角形的周长和面积分别相等 B. 全等三角形是指形状相同的两个三角形 C. 全等三角形是指面积相等的两个三角形 D. 所有的等边三角形都是全等三角形
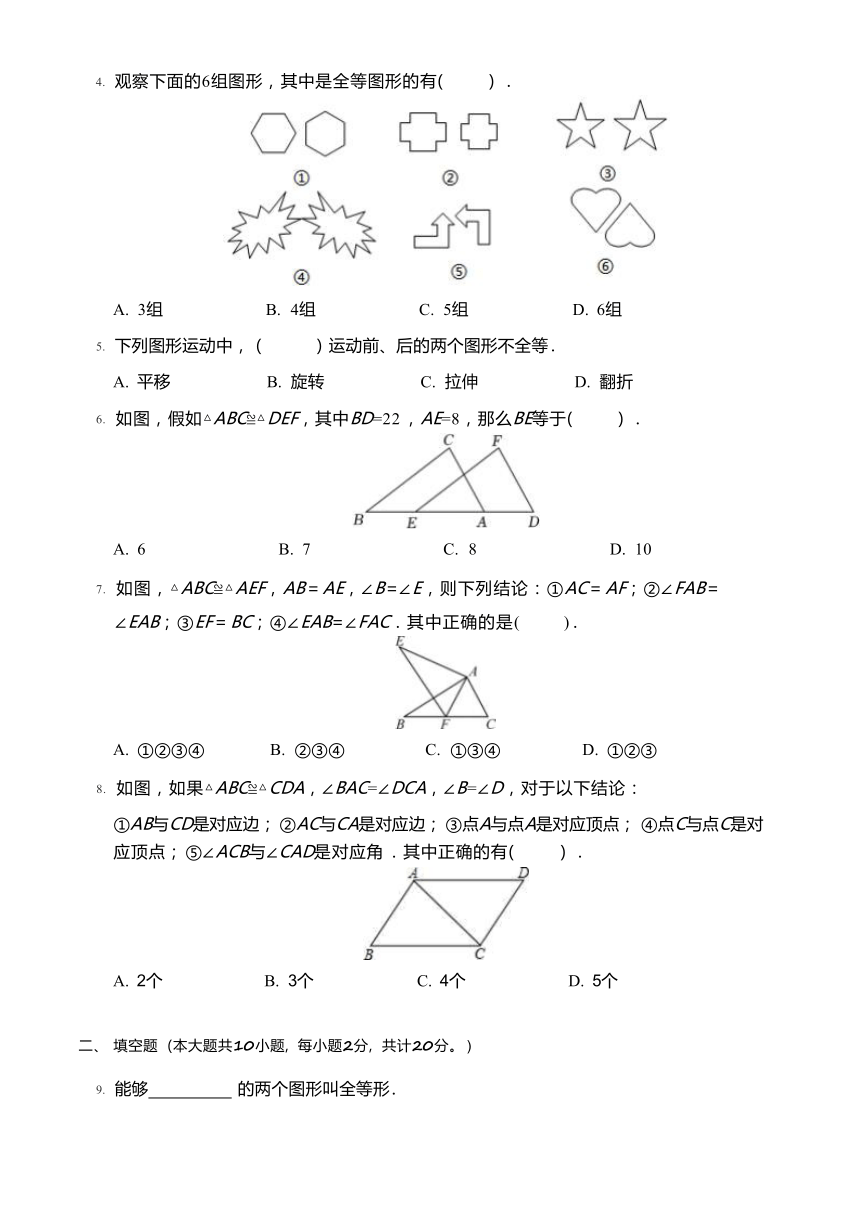
4. 观察下面的6组图形,其中是全等图形的有( ) .
A. 3组 B. 4组 C. 5组 D. 6组
5. 下列图形运动中,( )运动前、后的两个图形不全等 .
A. 平移 B. 旋转 C. 拉伸 D. 翻折
6. 如图,假如△ABC≌△DEF,其中BD=22 ,AE=8,那么BE等于( ) .
A. 6 B. 7 C. 8 D. 10
7. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:①AC=AF;②∠FAB =
∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的是( ) .
A. ①②③④ B. ②③④ C. ①③④ D. ①②③
8. 如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边; ②AC与CA是对应边; ③点A与点A是对应顶点; ④点C与点C是对 应顶点; ⑤∠ACB与∠CAD是对应角 .其中正确的有( ) .
A. 2个 B. 3个 C. 4个 D. 5个
二、 填空题 (本大题共10小题, 每小题2分, 共计20分。 )
9. 能够 的两个图形叫全等形 .
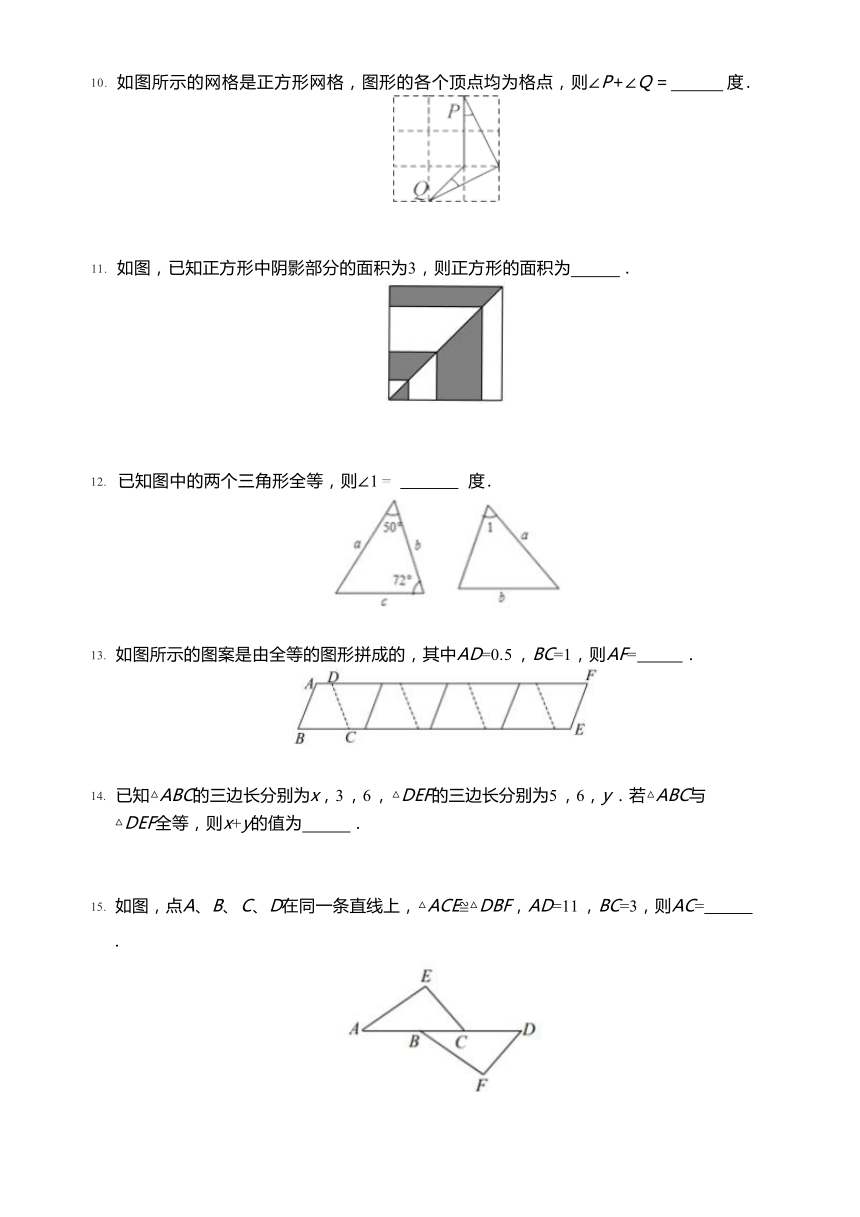
10. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠P+∠Q = 度 .
11. 如图,已知正方形中阴影部分的面积为3,则正方形的面积为 .
12. 已知图中的两个三角形全等,则∠1 度 .
13. 如图所示的图案是由全等的图形拼成的,其中AD=0.5 ,BC=1,则AF= .
14. 已知△ABC的三边长分别为x,3 ,6 , △DEF的三边长分别为5 ,6,y .若△ABC与 △DEF全等,则x+y的值为 .
15. 如图,点A、B、 C、D在同一条直线上,△ACE≌△DBF,AD=11 ,BC=3,则AC=
.
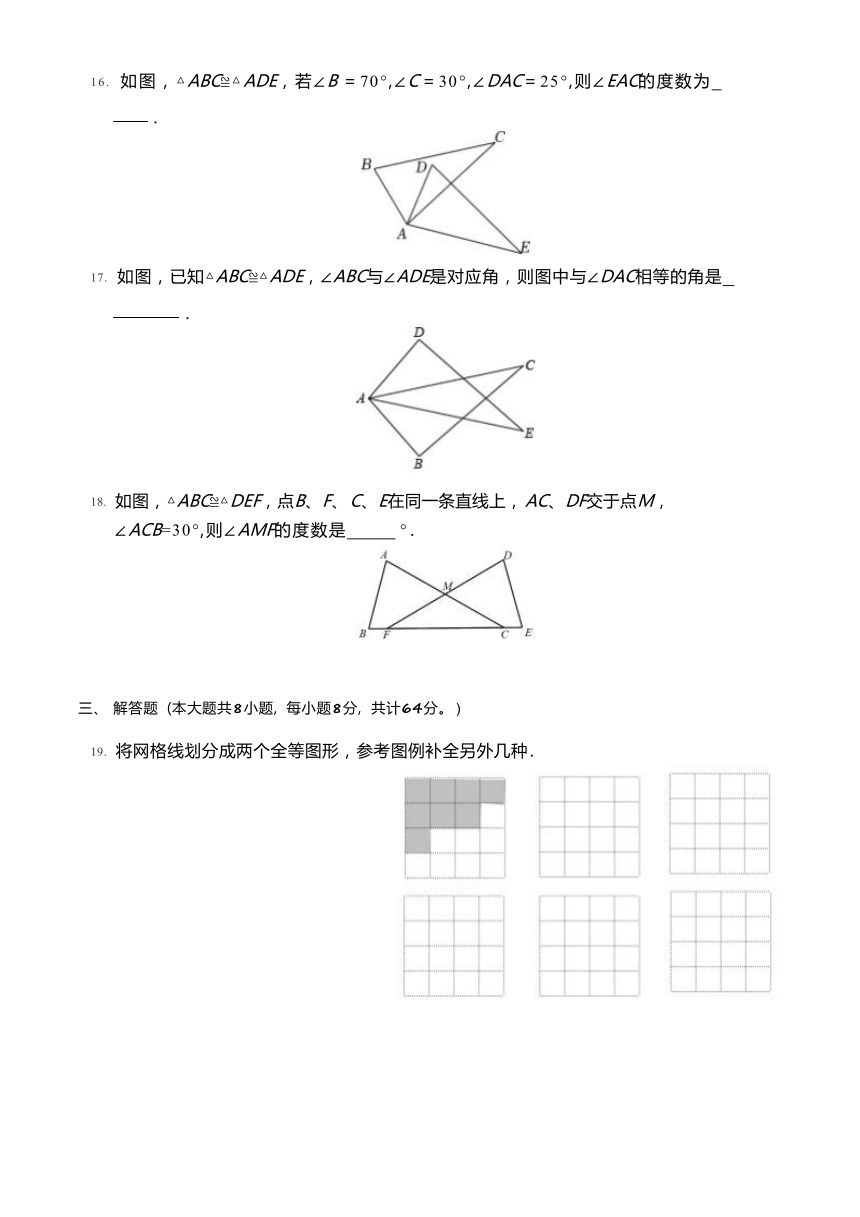
16. 如图,△ABC≌△ADE,若∠B =70°,∠C=30°,∠DAC=25°,则∠EAC的度数为
.
17. 如图,已知△ABC≌△ADE,∠ABC与∠ADE是对应角,则图中与∠DAC相等的角是
.
18. 如图,△ABC≌△DEF,点B、F、 C、E在同一条直线上, AC、DF交于点M, ∠ACB=30°,则∠AMF的度数是 ° .
三、 解答题 (本大题共8小题, 每小题8分, 共计64分。 )
19. 将网格线划分成两个全等图形,参考图例补全另外几种 .
20. 沿着图中的虚线,请将如图的图形分割成四个全等的图形 .
21. 如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,写出其他对应边及对应角 .
22. 如图所示, A,D,E三点在同一直线上,且△BAD≌△ACE,求证: BD=CE+DE.
23. 如图,点F、 G是正五边形ABCDE边BC、 CD上的点,连接AF、BG交于点H,且 △ABF≌△BCG .
(1)求∠EAB的大小;
(2)求∠AHG的大小 .
24. 如图所示,△ACD≌△ECD,△CEF≌△BEF,∠ACB =90° . 求∠B的度数 .
25. 如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系?请说明理由;
(2)当DE∥BC时,求∠AED的度数 .
26. 如图,已知△ABC≌△DEC,且点B,C,D在同一条直线上,延长DE交AB于点F.
(1)求证: DF⊥AB;
(2)已知BD=8 ,CE=3,求AE的长度 .
参考答案:
选择题
1-5:DBABC,6-8:BCB
填空题
9.完全重合
10.45
11.6
12.58
13.6
14.8
15.7
16.55°
∠BAE
60
解答题
参考下图,答案不唯一
答案见下图
解:∵△ABC≌△CDA
∴对应边AC和CA,对应角∠BAC和∠DCA,∠B和∠D,∠ACB和∠CAD
证明:∵△BAD≌△ACE
∴BD=AE,AD=CE
∵AE=AD+DE
∴BD=CE+DE
解:(1)∵五边形ABCDE是正五边形,
∴∠EAB= =108°
(2)∵△ABF≌△BCG
∴∠BAF=∠CBG
又∵∠AHG=∠BAF+∠ABH=∠CBG+∠ABH=∠ABC=∠EAB=108°
解:设∠B=
∵△ACD≌△ECD,△CEF≌△BEF
∴∠A=∠CED,∠B=∠3=
∴∠A=∠CED=∠B+∠3=2
∵∠A+∠B+∠ACB=180°
∴2 + +90°=180°
∴ =30°
即∠B=30°
25.解(1)DE=CE+BC,理由如下
∵△ABC≌△DAE
∴AE=BC,DE=AC
∵A、E、C三点在同一条直线上,
∴AC=AE+CE
∴DE=CE+BC
∵△ABC≌△DAE
∴∠AED=∠C
又∵DE∥BC
∴∠C=∠DEC
又∵∠AED+∠DEC=180°
∴∠AED=∠DEC=90°
∴当DE∥BC时,∠AED=90°
(1)证明:∵△ABC≌△DEC
∴∠BCA=∠ECD,∠BAC=∠EDC
∵点B、C、D在同一条直线上,
∴∠BCA=∠ECD=90°
∴∠CDE+∠CED=90°
∵∠AEF=∠CED
∴∠AEF+∠BAC=90°
∴∠AFE=90°即DF⊥AB
(2)解:∵△ABC≌△DEC
∴BC=CE=3,AC=DC
∴DC=BD-BC=8-3=5
∴AC=DC=5
∴AE=AC-CE=5-3=2
教材版本 苏科版 练习时间 90分钟 练习难度 ★★★☆☆
练习范围 主要对1.1全等图形, 1.2全等三角形相关知识进行练习
一、 选择题 (本大题共8小题, 每小题2分, 共计16分。 )
1. 下列说法错误的是( ) .
A. 如果两个图形全等,那么它们的形状和大小一定相同
B. 全等三角形的对应边相等,对应角相等
C. 图形全等,只与形状、大小有关,而与它们的位置无关
D. 面积相等的两个图形是全等图形
2. 下列图形:①两个正方形;②底边相等的两个等腰三角形;③每边都是2cm的两个三角
形;④半径都是1.5cm的两个圆 .其中是一对全等图形的有( ) .
A. 1个 B. 2个 C. 3个 D. 4个
3. 下列说法正确的是( ) .
A. 全等三角形的周长和面积分别相等 B. 全等三角形是指形状相同的两个三角形 C. 全等三角形是指面积相等的两个三角形 D. 所有的等边三角形都是全等三角形
4. 观察下面的6组图形,其中是全等图形的有( ) .
A. 3组 B. 4组 C. 5组 D. 6组
5. 下列图形运动中,( )运动前、后的两个图形不全等 .
A. 平移 B. 旋转 C. 拉伸 D. 翻折
6. 如图,假如△ABC≌△DEF,其中BD=22 ,AE=8,那么BE等于( ) .
A. 6 B. 7 C. 8 D. 10
7. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:①AC=AF;②∠FAB =
∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的是( ) .
A. ①②③④ B. ②③④ C. ①③④ D. ①②③
8. 如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边; ②AC与CA是对应边; ③点A与点A是对应顶点; ④点C与点C是对 应顶点; ⑤∠ACB与∠CAD是对应角 .其中正确的有( ) .
A. 2个 B. 3个 C. 4个 D. 5个
二、 填空题 (本大题共10小题, 每小题2分, 共计20分。 )
9. 能够 的两个图形叫全等形 .
10. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠P+∠Q = 度 .
11. 如图,已知正方形中阴影部分的面积为3,则正方形的面积为 .
12. 已知图中的两个三角形全等,则∠1 度 .
13. 如图所示的图案是由全等的图形拼成的,其中AD=0.5 ,BC=1,则AF= .
14. 已知△ABC的三边长分别为x,3 ,6 , △DEF的三边长分别为5 ,6,y .若△ABC与 △DEF全等,则x+y的值为 .
15. 如图,点A、B、 C、D在同一条直线上,△ACE≌△DBF,AD=11 ,BC=3,则AC=
.
16. 如图,△ABC≌△ADE,若∠B =70°,∠C=30°,∠DAC=25°,则∠EAC的度数为
.
17. 如图,已知△ABC≌△ADE,∠ABC与∠ADE是对应角,则图中与∠DAC相等的角是
.
18. 如图,△ABC≌△DEF,点B、F、 C、E在同一条直线上, AC、DF交于点M, ∠ACB=30°,则∠AMF的度数是 ° .
三、 解答题 (本大题共8小题, 每小题8分, 共计64分。 )
19. 将网格线划分成两个全等图形,参考图例补全另外几种 .
20. 沿着图中的虚线,请将如图的图形分割成四个全等的图形 .
21. 如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,写出其他对应边及对应角 .
22. 如图所示, A,D,E三点在同一直线上,且△BAD≌△ACE,求证: BD=CE+DE.
23. 如图,点F、 G是正五边形ABCDE边BC、 CD上的点,连接AF、BG交于点H,且 △ABF≌△BCG .
(1)求∠EAB的大小;
(2)求∠AHG的大小 .
24. 如图所示,△ACD≌△ECD,△CEF≌△BEF,∠ACB =90° . 求∠B的度数 .
25. 如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系?请说明理由;
(2)当DE∥BC时,求∠AED的度数 .
26. 如图,已知△ABC≌△DEC,且点B,C,D在同一条直线上,延长DE交AB于点F.
(1)求证: DF⊥AB;
(2)已知BD=8 ,CE=3,求AE的长度 .
参考答案:
选择题
1-5:DBABC,6-8:BCB
填空题
9.完全重合
10.45
11.6
12.58
13.6
14.8
15.7
16.55°
∠BAE
60
解答题
参考下图,答案不唯一
答案见下图
解:∵△ABC≌△CDA
∴对应边AC和CA,对应角∠BAC和∠DCA,∠B和∠D,∠ACB和∠CAD
证明:∵△BAD≌△ACE
∴BD=AE,AD=CE
∵AE=AD+DE
∴BD=CE+DE
解:(1)∵五边形ABCDE是正五边形,
∴∠EAB= =108°
(2)∵△ABF≌△BCG
∴∠BAF=∠CBG
又∵∠AHG=∠BAF+∠ABH=∠CBG+∠ABH=∠ABC=∠EAB=108°
解:设∠B=
∵△ACD≌△ECD,△CEF≌△BEF
∴∠A=∠CED,∠B=∠3=
∴∠A=∠CED=∠B+∠3=2
∵∠A+∠B+∠ACB=180°
∴2 + +90°=180°
∴ =30°
即∠B=30°
25.解(1)DE=CE+BC,理由如下
∵△ABC≌△DAE
∴AE=BC,DE=AC
∵A、E、C三点在同一条直线上,
∴AC=AE+CE
∴DE=CE+BC
∵△ABC≌△DAE
∴∠AED=∠C
又∵DE∥BC
∴∠C=∠DEC
又∵∠AED+∠DEC=180°
∴∠AED=∠DEC=90°
∴当DE∥BC时,∠AED=90°
(1)证明:∵△ABC≌△DEC
∴∠BCA=∠ECD,∠BAC=∠EDC
∵点B、C、D在同一条直线上,
∴∠BCA=∠ECD=90°
∴∠CDE+∠CED=90°
∵∠AEF=∠CED
∴∠AEF+∠BAC=90°
∴∠AFE=90°即DF⊥AB
(2)解:∵△ABC≌△DEC
∴BC=CE=3,AC=DC
∴DC=BD-BC=8-3=5
∴AC=DC=5
∴AE=AC-CE=5-3=2
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
