1.2 种群数量的变化 第1课时课件(共35张PPT2份视频) 2024-2025学年高二生物学人教版(2019)选择性必修2
文档属性
| 名称 | 1.2 种群数量的变化 第1课时课件(共35张PPT2份视频) 2024-2025学年高二生物学人教版(2019)选择性必修2 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2024-11-09 17:33:47 | ||
图片预览








文档简介
(共35张PPT)
第2节 种群数量的变化
第1课时
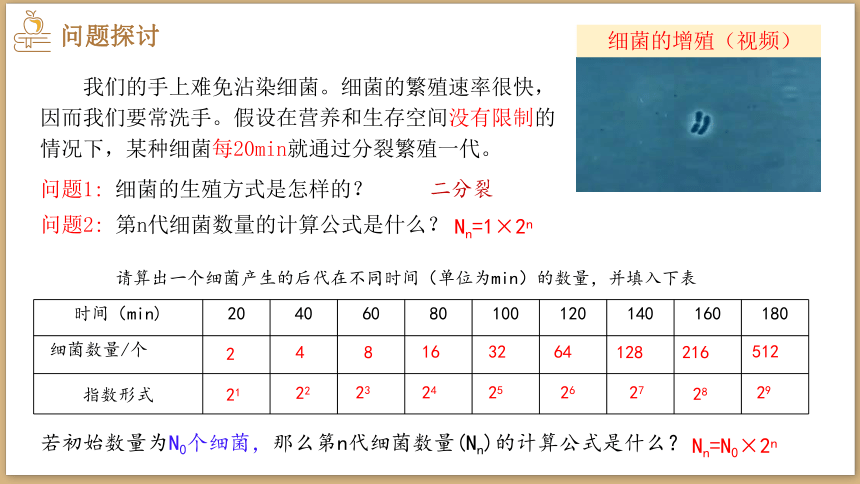
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
细菌的增殖(视频)
二分裂
问题1: 细菌的生殖方式是怎样的?
问题2: 第n代细菌数量的计算公式是什么?
Nn=1×2n
请算出一个细菌产生的后代在不同时间(单位为min)的数量,并填入下表
时间(min) 20 40 60 80 100 120 140 160 180
细菌数量/个
指数形式
21
22
23
24
25
26
27
28
29
2
4
8
16
32
64
128
216
512
若初始数量为N0个细菌,那么第n代细菌数量(Nn)的计算公式是什么?
Nn=N0×2n
n= 60min ×72h/20min=216
Nn=1 X 2n =2216
不会
建构模型
问题3: 72h后,由一个细菌分裂产生的细菌数量是多少?
问题4: 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?为了验证你的观点,我们可以采用什么学科方法来研究?
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
细菌的增殖(视频)
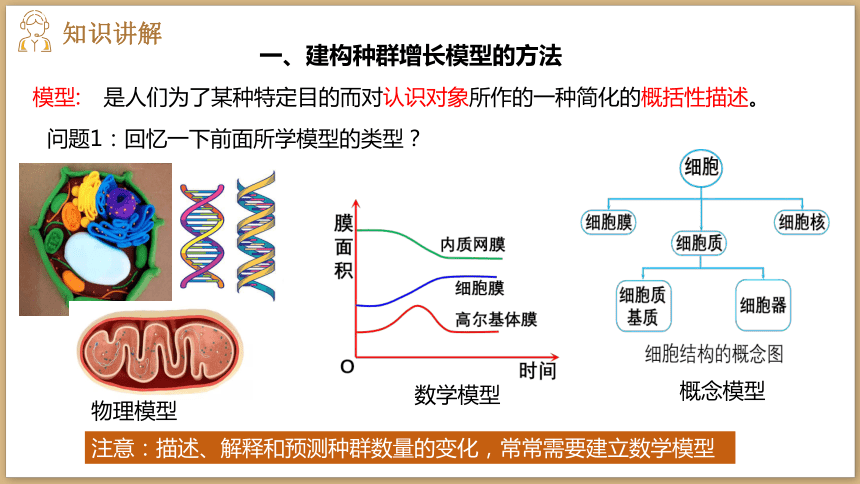
模型:
物理模型
数学模型
概念模型
注意:描述、解释和预测种群数量的变化,常常需要建立数学模型
是人们为了某种特定目的而对认识对象所作的一种简化的概括性描述。
问题1:回忆一下前面所学模型的类型?
SZ-LWH
一、建构种群增长模型的方法
观察分析
提出问题
提出假设
建立
数学模型
对模型进行检验修正
研究方法
研究实例
细菌每20min分裂一次,怎样计算繁殖n代的数量?
在资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察、统计细菌数量,对模型进行检验或修正
1.定义:
用来描述一个系统或它的性质的数学形式。
2.步骤:
建立数学模型
SZ-LWH
一、建构种群增长模型的方法——
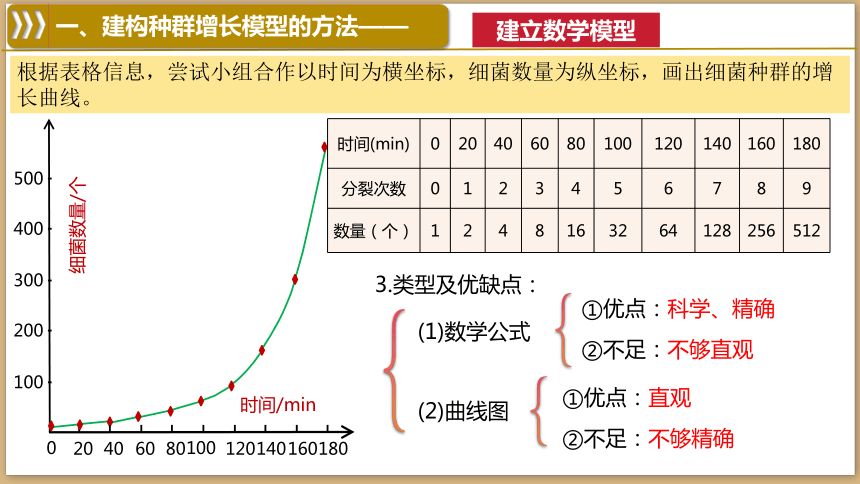
根据表格信息,尝试小组合作以时间为横坐标,细菌数量为纵坐标,画出细菌种群的增长曲线。
0
时间/min
细菌数量/个
100
200
300
400
500
20
40
60
80
100
120
140
160
180
时间(min) 0 20 40 60 80 100 120 140 160 180
分裂次数 0 1 2 3 4 5 6 7 8 9
数量(个) 1 2 4 8 16 32 64 128 256 512
3.类型及优缺点:
(1)数学公式
(2)曲线图
①优点:科学、精确
②不足:不够直观
①优点:直观
②不足:不够精确
建立数学模型
SZ-LWH
一、建构种群增长模型的方法——
阅读教材P8“思考●讨论”, 分析自然界种群增长的实例,小组合作完成以下问题。
1.两个资料中种群增长有什么共同点
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
自然界中种群的数量变化情况是怎样的呢?
分析自然界种群增长实例
思考.讨论
【资料1】1859年,一位来澳大利亚定居的英国人在他的农场中放生了24只野兔,一个世纪后,这24只野兔的后代竟超过6亿只。漫山遍野的野兔不仅与牛羊争食牧草,还啃噬树皮,造成植被破坏,导致水土流失。直到人们引入了黏液瘤病毒才使野兔的数量得到控制。
24只
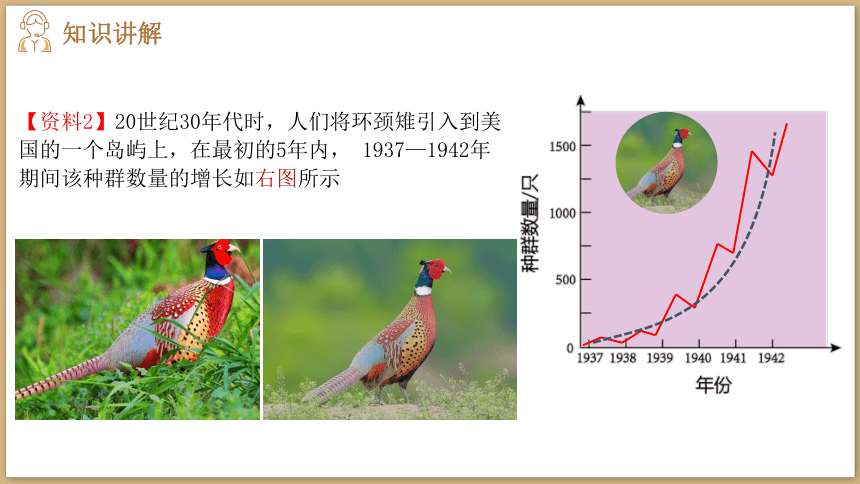
【资料2】20世纪30年代时,人们将环颈雉引入到美国的一个岛屿上,在最初的5年内, 1937—1942年期间该种群数量的增长如右图所示
1.两个资料中种群增长有什么共同点?
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
种群数量增长迅猛,且呈无限增长趋势。
食物充足、缺少天敌等。
不能,因为资源和空间是有限的。
思考.讨论
0
时间/min
细菌数量/个
100
200
300
400
500
20
40
60
80
100
120
140
160
180
二、种群的“J”形增长
自然界确有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈“J”形。
某海岛上环颈雉种群数量的变化
1.“J”形增长曲线的模型假设和适用对象分别是什么?
阅读教材P8-9,小组合作完成以下问题。
3.写出“J”形增长曲线的数学模型(以数学公式表示)及各字母的含义。
2.“J”形增长曲线的增长特点是怎样的?
4.查阅历年来世界和我国人口增长的数据,分析人口是否呈“J”形增长。
1.模型假设:
食物和空间条件充裕
气候适宜
没有天敌(捕食和寄生天敌)
没有其他竞争物种等
某种群
理想状态
种群数量每年以一定的倍数增长
第二年的数量是第一年的λ倍
什么情况会出现理想状态?
①实验室条件下;
②当一个种群刚迁入到一个新的适宜环境时 。
若第一年是N0,则第二年是多少?t年后呢?
2.“J”形增长的数学模型公式:
假设:
种群数量每年以一定的倍数(λ)增长。种群起始数量为N0
N1 = N0 λ
N2 = N1 λ =N0 λ2
N3 = N2 λ = N0λ3
Nt = N0 λt
t年后该种群的数量
种群的起始数量
每年增长倍数
时间
λ =
当年种群数量
前一年种群数量
曲线图:
时间(t)
种群数量Nt
数学模型:
3.“J”形增长的特点:
种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
只有λ>1且为定值时,种群增长才为“J”形增长。
4.“J”形增长的适用条件
据图分析,种群数量变化符合数学公式:Nt=N0λt时,种群增长曲线一定是“J”形吗?并说明理由。
当λ<1时,种群数量减少;
当λ=1时,种群数量相对稳定;
不一定
当λ>1时,种群数量增多
现学现用
① 1~4年,种群数量_______________
② 4~5年,种群数量_______________
③ 5~9年,种群数量_______________
④ 9~10年,种群数量______________
⑤ 10~11年,种群数量_____________
⑥ 11~13年,种群数量_____________
。
⑦ 前9年,种群数量第_______年最高
⑧ 9~13年,种群数量第______年最低
呈“J”形增长
增长
相对稳定
下降
下降
11~12下降,
5
12
据图说出种群数量如何变化
12~13增长
λ =
当年种群数量
前一年种群数量
5. 种群”J”形增长的实例
①外来入侵物种的种群数量变化
②动物迁入适宜其生活的新环境后,一段时间内种群的数量变化
③实验室中营养充分的情况
中国人口数据增长曲线
世界人口数据增长曲线
6.人口数据增长曲线:
人口在20世纪大部分时期呈现出“J”形增长
如果遇到资源、空间等方面的限制,种群还会呈“J”形增长吗?
【实例】生态学家高斯的实验
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履虫的数量。经反复实验,结果如下图所示。
第二天和第三天
第五天
问题2.第几天以后基本维持在375个左右?
问题1.大草履虫的数量在第几天增长较快?
【实例】生态学家高斯的实验
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履虫的数量。经反复实验,结果如下图所示。
问题3. 为什么大草履虫种群没有出现“J”形增长?
由于随着大草履虫数量的增多,对食物和空间的竞争趋于激烈,导致出生率下降,死亡率升高。
问题4.这种类型的种群增长称为什么?
种群的“S”形增长
1.什么是“S”形增长曲线?“S”形增长曲线的形成原因是什么?
阅读课本P9页相关内容,回答以下问题:
3.“S”形增长曲线的适用对象是什么?
2.“S”形增长曲线的增长有什么特点 尝试分析“S”形增长曲线各段的含义。
4.什么是环境容纳量(K值)?在生产实践活动中如何运用K值?
三、种群的“S”形增长
三、种群的“S”形增长
1.概念:
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形。
2.“S”形增长形成原因:
现实状态
①资源和空间有限
②种群密度增大时,
种内竞争加剧
出生率下降
死亡率升高
出生率=死亡率
种群稳定在一定的水平
此时种群达到的最大数量称为什么?
3.环境容纳量:
一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K 值。
思考1. K值是不是种群数量的最大值?
不是;K值是种群在一定环境条件下所能维持(允许达到)的种群最大数量
思考2.同一种群的K值是固定不变的吗?
不是一成不变的:K值会随着环境的改变而发生变化,当环境遭到破坏时,K值会下降;当环境条件状况改善时,K值会上升。
4.“S”曲线的分析:
B
C
D
E
A
种群基数小,需要适应新环境,增长较缓慢。
(1)AB段:
(2)BC段:
(3)C点:
(4)CD段:
资源和空间丰富,出生率升高,种群数量增长迅速。
种群数量为K/2,种群增长速率达到最大。
资源和空间有限,种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓;
调整期
加速期
转折期
减速期
(5)DE段:
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。
饱和期
5.“S”曲线的增长特点:
S型曲线增长速率曲线
增长速率
时间
t1
t2
①增长速率先 后 ,最后为 。
②当种群数量为 时,增长速率达到最大。
K/2
K
A
B
C
D
E
请以时间为横坐标,种群增长速率为纵坐标,画出种群“S”形增长的增长速率曲线。
增大
减小
0
k/2
增长率与增长速率
增长率
增长速率
指种群数量在单位时间内的改变数值,有单位。(如个/年等)
指在单位时间内种群数量增加的量占初始数量的比例,是一个百分比,无单位。
例:某一种群的数量在某一单位时间t(如一年)内,由初数量Nt-1(个)增长到末数量Nt(个),则这一单位时间内种群的增长率和增长速率的计算分别为:
增长速率=
末数-初数
单位时间
=
Nt-Nt-1(个)
t(年)
×100%
增长率=
末数-初数
=
Nt-Nt-1
初数
Nt-1
=出生率-死亡率
= λ-1
拓展延伸
种群增长率
时间
t1
t2
O
种群增长速率
时间
t1
t2
O
“J”形曲线增长率
“S”形曲线增长率
“J”形曲线增长速率
“S”形曲线增长速率
请根据“J”形增长曲线和“S”形增长曲线,画出相应的增长率曲线和增长速率曲线
1.如图表示一个区域内甲、乙两个种群的增长速率随时间变化的曲线,下列有关叙述正确的是( )
A.据图可知,乙种群的K值大于甲种群的K值
B.t3~t5时间内甲、乙两种群的年龄结构不同
C.t2~t3时间内甲种群出生率小于死亡率
D.t4时乙的种群密度最大
B
①野生大熊猫种群数量锐减的关键原因是什么?
②保护大熊猫的根本措施是什么?
建立自然保护区,改善栖息环境,从而提高环境容纳量。
野生大熊猫的栖息地遭到破坏,食物和活动范围缩小,K值降低。
6.K值和K/2值的运用:
增大环境阻力→降低K值→防治老鼠
断绝或减少它们的食物来源
养殖或释放它们的天敌
③鼠害导致作物减产,蚊、蝇会传播疾病。从环境容纳量的角度思考,对家鼠等有害动物的控制,应当采取什么措施?
防止老鼠种群数量达到K/2处
6.K值和K/2值的运用:
④为了保护鱼类资源不受破坏,并能持续地获得最大捕鱼量,应使被捕鱼群的种群数量保持在什么水平?为什么?
应使被捕鱼群的种群数量保持在K/2水平,因为在这个水平上种群增长速率最大。
6.K值和K/2值的运用:
K
种群数量
时间
0
B
C
D
E
t1
t2
A
K/2
——“黄金开发点”
6.K值和K/2值的运用:
K值
减小环境阻力 → 增大K值 → 保护野生生物资源
增大环境阻力 → 降低K值 → 防治有害生物
草原最大载畜量不超过K值 → 合理确定载畜量
K/2值
渔业捕捞后的种群数量要在K/2值处
K/2值前防治有害生物,严防达到K/2值处
“J”形增长 “S”形增长
条件
模型
增长速率
有无K值
增长倍数
食物和空间条件充裕、气候适宜、没有敌害(即无环境阻力)
资源和空间有限,天敌的制约等(即存在环境阻力)
Nt=N0λt
无
有
λ为大于1的定值
增长倍数大于1,不是定值
种群增长的“J”形增长与“S”形增长的比较
两种增长曲线的主要差异是:
环境阻力不同
生存斗争中被淘汰的个体数
环境阻力
第2节 种群数量的变化
第1课时
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
细菌的增殖(视频)
二分裂
问题1: 细菌的生殖方式是怎样的?
问题2: 第n代细菌数量的计算公式是什么?
Nn=1×2n
请算出一个细菌产生的后代在不同时间(单位为min)的数量,并填入下表
时间(min) 20 40 60 80 100 120 140 160 180
细菌数量/个
指数形式
21
22
23
24
25
26
27
28
29
2
4
8
16
32
64
128
216
512
若初始数量为N0个细菌,那么第n代细菌数量(Nn)的计算公式是什么?
Nn=N0×2n
n= 60min ×72h/20min=216
Nn=1 X 2n =2216
不会
建构模型
问题3: 72h后,由一个细菌分裂产生的细菌数量是多少?
问题4: 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?为了验证你的观点,我们可以采用什么学科方法来研究?
我们的手上难免沾染细菌。细菌的繁殖速率很快,因而我们要常洗手。假设在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
细菌的增殖(视频)
模型:
物理模型
数学模型
概念模型
注意:描述、解释和预测种群数量的变化,常常需要建立数学模型
是人们为了某种特定目的而对认识对象所作的一种简化的概括性描述。
问题1:回忆一下前面所学模型的类型?
SZ-LWH
一、建构种群增长模型的方法
观察分析
提出问题
提出假设
建立
数学模型
对模型进行检验修正
研究方法
研究实例
细菌每20min分裂一次,怎样计算繁殖n代的数量?
在资源和生存空间没有限制的条件下,细菌种群的增长不会受种群密度增加的影响
Nn=2n
N代表细菌数量,n表示第几代
观察、统计细菌数量,对模型进行检验或修正
1.定义:
用来描述一个系统或它的性质的数学形式。
2.步骤:
建立数学模型
SZ-LWH
一、建构种群增长模型的方法——
根据表格信息,尝试小组合作以时间为横坐标,细菌数量为纵坐标,画出细菌种群的增长曲线。
0
时间/min
细菌数量/个
100
200
300
400
500
20
40
60
80
100
120
140
160
180
时间(min) 0 20 40 60 80 100 120 140 160 180
分裂次数 0 1 2 3 4 5 6 7 8 9
数量(个) 1 2 4 8 16 32 64 128 256 512
3.类型及优缺点:
(1)数学公式
(2)曲线图
①优点:科学、精确
②不足:不够直观
①优点:直观
②不足:不够精确
建立数学模型
SZ-LWH
一、建构种群增长模型的方法——
阅读教材P8“思考●讨论”, 分析自然界种群增长的实例,小组合作完成以下问题。
1.两个资料中种群增长有什么共同点
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
自然界中种群的数量变化情况是怎样的呢?
分析自然界种群增长实例
思考.讨论
【资料1】1859年,一位来澳大利亚定居的英国人在他的农场中放生了24只野兔,一个世纪后,这24只野兔的后代竟超过6亿只。漫山遍野的野兔不仅与牛羊争食牧草,还啃噬树皮,造成植被破坏,导致水土流失。直到人们引入了黏液瘤病毒才使野兔的数量得到控制。
24只
【资料2】20世纪30年代时,人们将环颈雉引入到美国的一个岛屿上,在最初的5年内, 1937—1942年期间该种群数量的增长如右图所示
1.两个资料中种群增长有什么共同点?
2.种群出现这种增长的原因是什么?
3.这种种群增长的趋势能不能一直持续下去?为什么?
种群数量增长迅猛,且呈无限增长趋势。
食物充足、缺少天敌等。
不能,因为资源和空间是有限的。
思考.讨论
0
时间/min
细菌数量/个
100
200
300
400
500
20
40
60
80
100
120
140
160
180
二、种群的“J”形增长
自然界确有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈“J”形。
某海岛上环颈雉种群数量的变化
1.“J”形增长曲线的模型假设和适用对象分别是什么?
阅读教材P8-9,小组合作完成以下问题。
3.写出“J”形增长曲线的数学模型(以数学公式表示)及各字母的含义。
2.“J”形增长曲线的增长特点是怎样的?
4.查阅历年来世界和我国人口增长的数据,分析人口是否呈“J”形增长。
1.模型假设:
食物和空间条件充裕
气候适宜
没有天敌(捕食和寄生天敌)
没有其他竞争物种等
某种群
理想状态
种群数量每年以一定的倍数增长
第二年的数量是第一年的λ倍
什么情况会出现理想状态?
①实验室条件下;
②当一个种群刚迁入到一个新的适宜环境时 。
若第一年是N0,则第二年是多少?t年后呢?
2.“J”形增长的数学模型公式:
假设:
种群数量每年以一定的倍数(λ)增长。种群起始数量为N0
N1 = N0 λ
N2 = N1 λ =N0 λ2
N3 = N2 λ = N0λ3
Nt = N0 λt
t年后该种群的数量
种群的起始数量
每年增长倍数
时间
λ =
当年种群数量
前一年种群数量
曲线图:
时间(t)
种群数量Nt
数学模型:
3.“J”形增长的特点:
种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
只有λ>1且为定值时,种群增长才为“J”形增长。
4.“J”形增长的适用条件
据图分析,种群数量变化符合数学公式:Nt=N0λt时,种群增长曲线一定是“J”形吗?并说明理由。
当λ<1时,种群数量减少;
当λ=1时,种群数量相对稳定;
不一定
当λ>1时,种群数量增多
现学现用
① 1~4年,种群数量_______________
② 4~5年,种群数量_______________
③ 5~9年,种群数量_______________
④ 9~10年,种群数量______________
⑤ 10~11年,种群数量_____________
⑥ 11~13年,种群数量_____________
。
⑦ 前9年,种群数量第_______年最高
⑧ 9~13年,种群数量第______年最低
呈“J”形增长
增长
相对稳定
下降
下降
11~12下降,
5
12
据图说出种群数量如何变化
12~13增长
λ =
当年种群数量
前一年种群数量
5. 种群”J”形增长的实例
①外来入侵物种的种群数量变化
②动物迁入适宜其生活的新环境后,一段时间内种群的数量变化
③实验室中营养充分的情况
中国人口数据增长曲线
世界人口数据增长曲线
6.人口数据增长曲线:
人口在20世纪大部分时期呈现出“J”形增长
如果遇到资源、空间等方面的限制,种群还会呈“J”形增长吗?
【实例】生态学家高斯的实验
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履虫的数量。经反复实验,结果如下图所示。
第二天和第三天
第五天
问题2.第几天以后基本维持在375个左右?
问题1.大草履虫的数量在第几天增长较快?
【实例】生态学家高斯的实验
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履虫的数量。经反复实验,结果如下图所示。
问题3. 为什么大草履虫种群没有出现“J”形增长?
由于随着大草履虫数量的增多,对食物和空间的竞争趋于激烈,导致出生率下降,死亡率升高。
问题4.这种类型的种群增长称为什么?
种群的“S”形增长
1.什么是“S”形增长曲线?“S”形增长曲线的形成原因是什么?
阅读课本P9页相关内容,回答以下问题:
3.“S”形增长曲线的适用对象是什么?
2.“S”形增长曲线的增长有什么特点 尝试分析“S”形增长曲线各段的含义。
4.什么是环境容纳量(K值)?在生产实践活动中如何运用K值?
三、种群的“S”形增长
三、种群的“S”形增长
1.概念:
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形。
2.“S”形增长形成原因:
现实状态
①资源和空间有限
②种群密度增大时,
种内竞争加剧
出生率下降
死亡率升高
出生率=死亡率
种群稳定在一定的水平
此时种群达到的最大数量称为什么?
3.环境容纳量:
一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K 值。
思考1. K值是不是种群数量的最大值?
不是;K值是种群在一定环境条件下所能维持(允许达到)的种群最大数量
思考2.同一种群的K值是固定不变的吗?
不是一成不变的:K值会随着环境的改变而发生变化,当环境遭到破坏时,K值会下降;当环境条件状况改善时,K值会上升。
4.“S”曲线的分析:
B
C
D
E
A
种群基数小,需要适应新环境,增长较缓慢。
(1)AB段:
(2)BC段:
(3)C点:
(4)CD段:
资源和空间丰富,出生率升高,种群数量增长迅速。
种群数量为K/2,种群增长速率达到最大。
资源和空间有限,种群密度增大,种内竞争加剧,出生率降低,死亡率升高,种群增长减缓;
调整期
加速期
转折期
减速期
(5)DE段:
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持相对稳定。
饱和期
5.“S”曲线的增长特点:
S型曲线增长速率曲线
增长速率
时间
t1
t2
①增长速率先 后 ,最后为 。
②当种群数量为 时,增长速率达到最大。
K/2
K
A
B
C
D
E
请以时间为横坐标,种群增长速率为纵坐标,画出种群“S”形增长的增长速率曲线。
增大
减小
0
k/2
增长率与增长速率
增长率
增长速率
指种群数量在单位时间内的改变数值,有单位。(如个/年等)
指在单位时间内种群数量增加的量占初始数量的比例,是一个百分比,无单位。
例:某一种群的数量在某一单位时间t(如一年)内,由初数量Nt-1(个)增长到末数量Nt(个),则这一单位时间内种群的增长率和增长速率的计算分别为:
增长速率=
末数-初数
单位时间
=
Nt-Nt-1(个)
t(年)
×100%
增长率=
末数-初数
=
Nt-Nt-1
初数
Nt-1
=出生率-死亡率
= λ-1
拓展延伸
种群增长率
时间
t1
t2
O
种群增长速率
时间
t1
t2
O
“J”形曲线增长率
“S”形曲线增长率
“J”形曲线增长速率
“S”形曲线增长速率
请根据“J”形增长曲线和“S”形增长曲线,画出相应的增长率曲线和增长速率曲线
1.如图表示一个区域内甲、乙两个种群的增长速率随时间变化的曲线,下列有关叙述正确的是( )
A.据图可知,乙种群的K值大于甲种群的K值
B.t3~t5时间内甲、乙两种群的年龄结构不同
C.t2~t3时间内甲种群出生率小于死亡率
D.t4时乙的种群密度最大
B
①野生大熊猫种群数量锐减的关键原因是什么?
②保护大熊猫的根本措施是什么?
建立自然保护区,改善栖息环境,从而提高环境容纳量。
野生大熊猫的栖息地遭到破坏,食物和活动范围缩小,K值降低。
6.K值和K/2值的运用:
增大环境阻力→降低K值→防治老鼠
断绝或减少它们的食物来源
养殖或释放它们的天敌
③鼠害导致作物减产,蚊、蝇会传播疾病。从环境容纳量的角度思考,对家鼠等有害动物的控制,应当采取什么措施?
防止老鼠种群数量达到K/2处
6.K值和K/2值的运用:
④为了保护鱼类资源不受破坏,并能持续地获得最大捕鱼量,应使被捕鱼群的种群数量保持在什么水平?为什么?
应使被捕鱼群的种群数量保持在K/2水平,因为在这个水平上种群增长速率最大。
6.K值和K/2值的运用:
K
种群数量
时间
0
B
C
D
E
t1
t2
A
K/2
——“黄金开发点”
6.K值和K/2值的运用:
K值
减小环境阻力 → 增大K值 → 保护野生生物资源
增大环境阻力 → 降低K值 → 防治有害生物
草原最大载畜量不超过K值 → 合理确定载畜量
K/2值
渔业捕捞后的种群数量要在K/2值处
K/2值前防治有害生物,严防达到K/2值处
“J”形增长 “S”形增长
条件
模型
增长速率
有无K值
增长倍数
食物和空间条件充裕、气候适宜、没有敌害(即无环境阻力)
资源和空间有限,天敌的制约等(即存在环境阻力)
Nt=N0λt
无
有
λ为大于1的定值
增长倍数大于1,不是定值
种群增长的“J”形增长与“S”形增长的比较
两种增长曲线的主要差异是:
环境阻力不同
生存斗争中被淘汰的个体数
环境阻力
