3.1.1 函数的定义与函数值同步学案
文档属性
| 名称 | 3.1.1 函数的定义与函数值同步学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 906.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 15:26:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.1.1 函数的定义与函数值同步学案
列清单·划重点
知识点1 函数的定义
一般的,如果在一个变化过程中有两个变量x和y,并且对于变量x在某一范围内的_______________,变量 y都有唯一确定的值与它__________,那么我们就称 y是x的函数,其中x 是自变量,y是因变量.
知识点2 函数值的定义
对于自变量 x在可以_______________的一个确定的值a,函数 y有______确定的对应值,这个对应值叫做当x=a时函数的值,简称函数值.
明考点·识方法
考点1 函数的定义
典例1 下列四个图象中,y不是x的函数的是 ( )
变式 下列关系中,y不是x 的函数的是 ( )
考点2 求函数关系式
典例2 油箱中存油40升,油从油箱中均匀流出,流速为 0.2升/分钟,则油箱中剩余油量 Q(升)与流出时间 t(分钟)的函数关系是 ( )
变式 为了加强公民节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 吨时,水价为每吨1.2元;超过10 吨时,超过的部分按每吨1.8元收费,现有某户居民5月份用水 12吨,应交水费________元.
考点3 与函数值有关的问题
典例3 当x=-2时,求下列函数y的对应值.
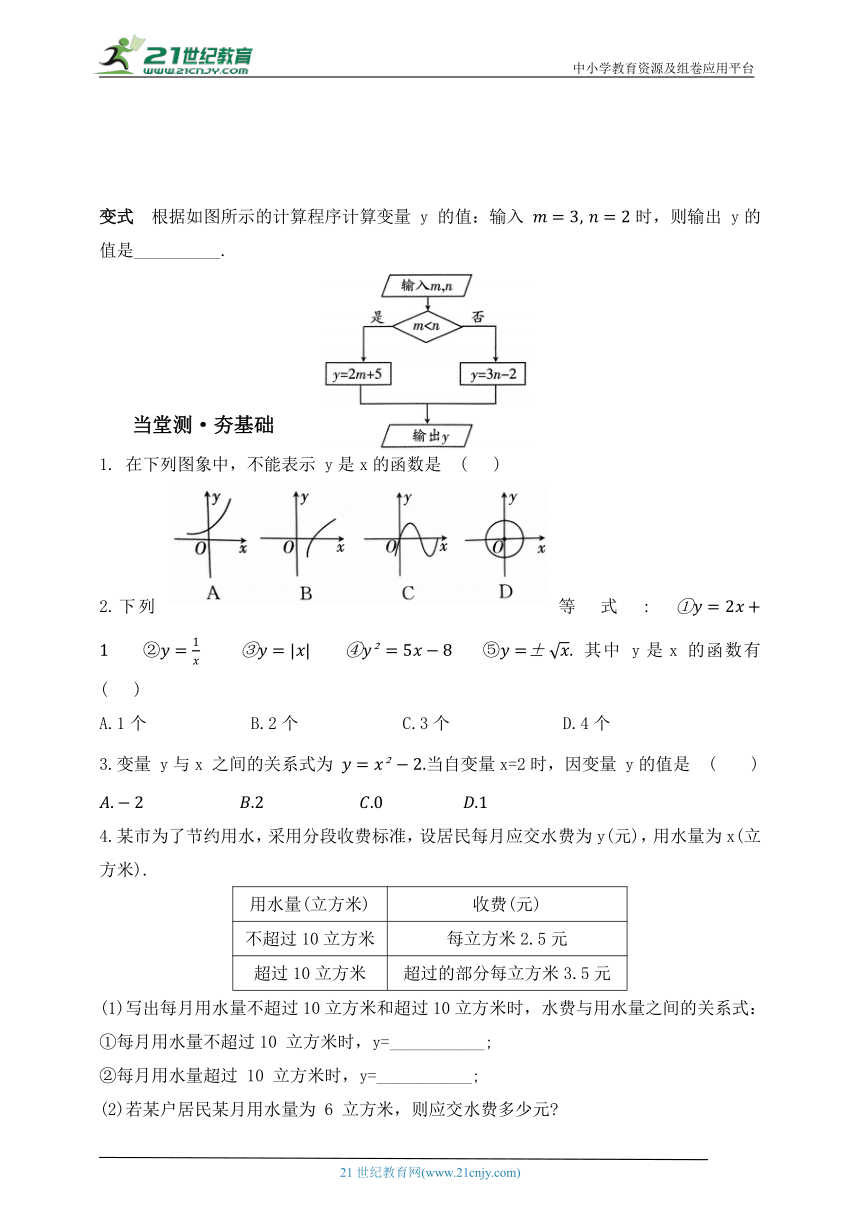
变式 根据如图所示的计算程序计算变量 y 的值:输入 时,则输出 y的值是__________.
当堂测·夯基础
在下列图象中,不能表示 y是x的函数是 ( )
2.下列等式: 其中 y是x 的函数有 ( )
A.1个 B.2个 C.3个 D.4个
3.变量 y与x 之间的关系式为 当自变量x=2时,因变量 y的值是 ( )
4.某市为了节约用水,采用分段收费标准,设居民每月应交水费为y(元),用水量为x(立方米).
用水量(立方米) 收费(元)
不超过10立方米 每立方米2.5元
超过10立方米 超过的部分每立方米3.5元
(1)写出每月用水量不超过10立方米和超过10立方米时,水费与用水量之间的关系式:
①每月用水量不超过10 立方米时,y=___________;
②每月用水量超过 10 立方米时,y=___________;
(2)若某户居民某月用水量为 6 立方米,则应交水费多少元
(3)若某户居民某月交水费32 元,则该户居民用水多少立方米
参考答案
【列清单·划重点】
知识点 1 每一个确定值 对应
知识点 2 取值范围内 唯一
【明考点·识方法】
典例1 D 变式 D
典例2 B 变式 15.6
典例3 解:(1)当x=-2时,
(2)当x=-2时,
变式 4
【当堂测·夯基础】
1. D 2. C 3. B
4.解:(1)①当0≤x≤10时,y=2.5x.故答案为:2.5x;
②当x>10时,y=2.5×10+3.5(x-10)=3.5x-10.故答案为:3.5x-10;
(2)当x=6时,y=2.5×6=15(元).所以,应交水费15元;
(3)2.5×10=25(元),32>25,∴该户居民月用水量超出 10 立方米.
当 y=32时,3.5x-10=32,解得x=12.所以,该户居民用水 12 立方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1.1 函数的定义与函数值同步学案
列清单·划重点
知识点1 函数的定义
一般的,如果在一个变化过程中有两个变量x和y,并且对于变量x在某一范围内的_______________,变量 y都有唯一确定的值与它__________,那么我们就称 y是x的函数,其中x 是自变量,y是因变量.
知识点2 函数值的定义
对于自变量 x在可以_______________的一个确定的值a,函数 y有______确定的对应值,这个对应值叫做当x=a时函数的值,简称函数值.
明考点·识方法
考点1 函数的定义
典例1 下列四个图象中,y不是x的函数的是 ( )
变式 下列关系中,y不是x 的函数的是 ( )
考点2 求函数关系式
典例2 油箱中存油40升,油从油箱中均匀流出,流速为 0.2升/分钟,则油箱中剩余油量 Q(升)与流出时间 t(分钟)的函数关系是 ( )
变式 为了加强公民节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 吨时,水价为每吨1.2元;超过10 吨时,超过的部分按每吨1.8元收费,现有某户居民5月份用水 12吨,应交水费________元.
考点3 与函数值有关的问题
典例3 当x=-2时,求下列函数y的对应值.
变式 根据如图所示的计算程序计算变量 y 的值:输入 时,则输出 y的值是__________.
当堂测·夯基础
在下列图象中,不能表示 y是x的函数是 ( )
2.下列等式: 其中 y是x 的函数有 ( )
A.1个 B.2个 C.3个 D.4个
3.变量 y与x 之间的关系式为 当自变量x=2时,因变量 y的值是 ( )
4.某市为了节约用水,采用分段收费标准,设居民每月应交水费为y(元),用水量为x(立方米).
用水量(立方米) 收费(元)
不超过10立方米 每立方米2.5元
超过10立方米 超过的部分每立方米3.5元
(1)写出每月用水量不超过10立方米和超过10立方米时,水费与用水量之间的关系式:
①每月用水量不超过10 立方米时,y=___________;
②每月用水量超过 10 立方米时,y=___________;
(2)若某户居民某月用水量为 6 立方米,则应交水费多少元
(3)若某户居民某月交水费32 元,则该户居民用水多少立方米
参考答案
【列清单·划重点】
知识点 1 每一个确定值 对应
知识点 2 取值范围内 唯一
【明考点·识方法】
典例1 D 变式 D
典例2 B 变式 15.6
典例3 解:(1)当x=-2时,
(2)当x=-2时,
变式 4
【当堂测·夯基础】
1. D 2. C 3. B
4.解:(1)①当0≤x≤10时,y=2.5x.故答案为:2.5x;
②当x>10时,y=2.5×10+3.5(x-10)=3.5x-10.故答案为:3.5x-10;
(2)当x=6时,y=2.5×6=15(元).所以,应交水费15元;
(3)2.5×10=25(元),32>25,∴该户居民月用水量超出 10 立方米.
当 y=32时,3.5x-10=32,解得x=12.所以,该户居民用水 12 立方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
