物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器 课件(共17张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器 课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-09 15:21:35 | ||
图片预览




文档简介
(共17张PPT)
1.4 质谱仪与回旋加速器
怎么分开电荷量相同,但质量不同的带电粒子?
质谱仪
阿斯顿
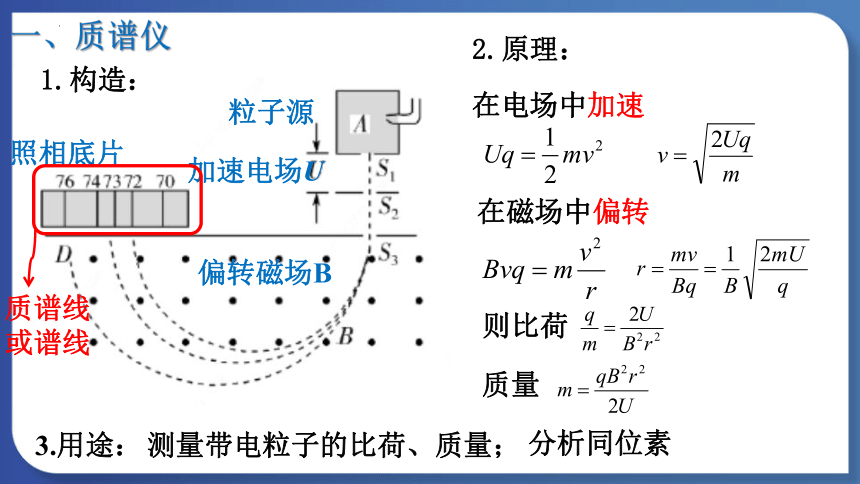
一、质谱仪
一、质谱仪
粒子源
加速电场U
偏转磁场B
照相底片
2.原理:
在电场中加速
在磁场中偏转
质谱线或谱线
则比荷
质量
3.用途:
1.构造:
测量带电粒子的比荷、质量;
分析同位素
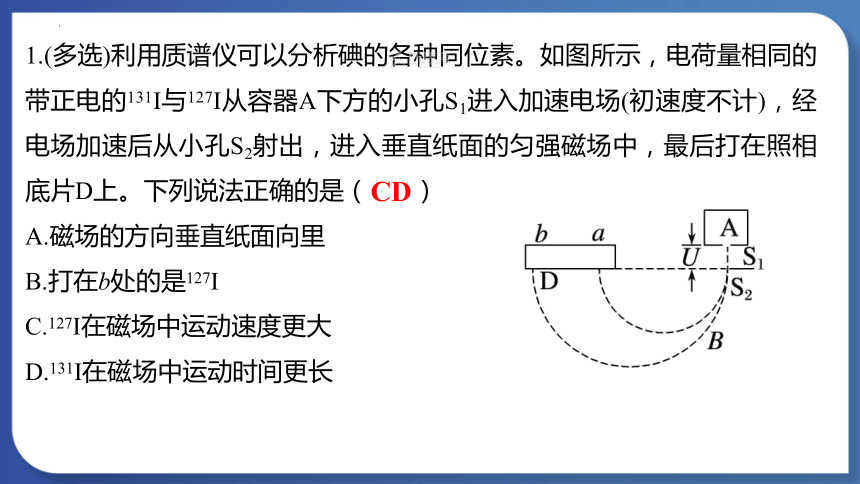
1.(多选)利用质谱仪可以分析碘的各种同位素。如图所示,电荷量相同的带正电的131I与127I从容器A下方的小孔S1进入加速电场(初速度不计),经电场加速后从小孔S2射出,进入垂直纸面的匀强磁场中,最后打在照相底片D上。下列说法正确的是( )
A.磁场的方向垂直纸面向里
B.打在b处的是127I
C.127I在磁场中运动速度更大
D.131I在磁场中运动时间更长
CD
2.质谱仪的原理图如图所示,由加速电场、速度选择器和偏转磁场组成。在速度选择器中存在相互垂直的匀强电场和匀强磁场(图中未画出)。偏转磁场是一个以直线MN为边界、方向垂直纸面向外、磁感应强度大小为B2的匀强磁场。一电荷量为q、质量为m的带正电的粒子从静止开始经过加速电场后,进入速度选择器,并能沿直线穿过速度选择器,从A点垂直MN进入偏转磁场。带电粒子经偏转磁场后,最终到达照相底片的C点。已知速度选择器中的电场方向水平向右、电场强度大小为E,A点到C点的距离为x,
带电粒子所受的重力可忽略不计。求:
(1)粒子进入偏转磁场的速度大小v;
(2)速度选择器中匀强磁场的磁感应强度B1的大小和方向;
(3)加速电场的电势差U。
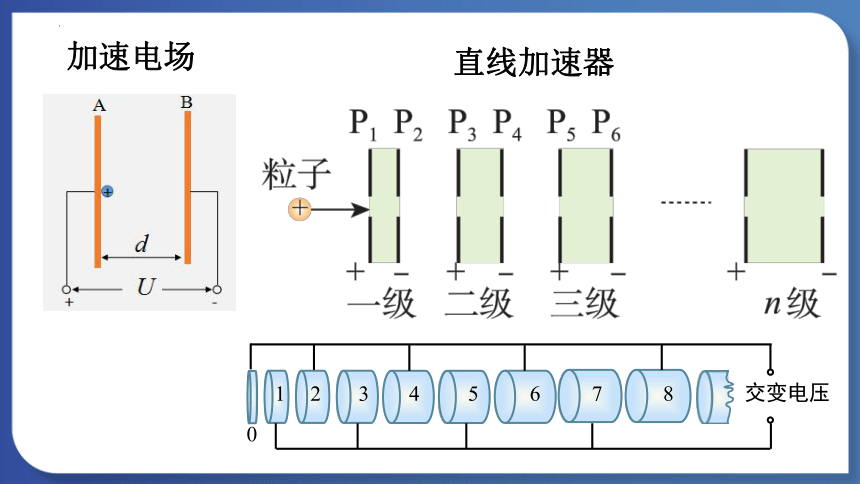
直线加速器
0
1
2
3
4
5
6
7
8
交变电压
加速电场
斯坦福大学加速器
北京正负电子对撞机
直线加速器占地空间非常大,有的长达几十千米,坐落在两个城市之间
欧内斯特·劳伦斯与他自己发明的回旋加速器
二、回旋加速器
二、回旋加速器
1.构造:
二、回旋加速器
1.构造:
2.原理:
(1)粒子经电场加速,经磁场回旋
(2)加速条件:
交流电源的周期等于粒子做圆周运动的周期
一个周期内,粒子加速 次
二、回旋加速器
1.构造:
2.原理:
(3)最大动能:
若D形盒半径为R
对某种粒子q、m一定,粒子获得的最大动能由磁感应强度B和回旋加速器的半径R决定,与加速度电压的大小无关。
二、回旋加速器
1.构造:
2.原理:
(4)加速次数:
(5)运动时间:
加速时间:
回旋时间:
回旋加速器不可无限加速。
粒子速度v接近光速c时,质量变大,在磁场中运动周期改变,与交变电场周期不同步。
只要不断增大回旋加速器的半径R,就能不断提高粒子获得的速度吗?
实际上,回旋加速器加速的带电粒子,能量达到25~30MeV后,就很难再加速了
3.某小型医用回旋加速器,最大回旋半径为0.5 m,磁感应强度大小为1.12 T,质子加速后获得的最大动能为1.5×107 eV。根据给出的数据,可计算质子经该回旋加速器加速后的最大速率约为( )
(忽略相对论效应,1 eV=1.6×10-19 J)
A.3.6×106 m/s B.1.2×107 m/s
C.5.4×107 m/s D.2.4×108 m/s
C
4.(多选)如图所示为回旋加速器示意图,利用回旋加速器对粒子(电荷量和质子相等,质量为质子的2倍)进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T。忽略粒子在D形盒缝隙间的运动时间和相对论效应,下列说法正确的是( )
A.保持B和T不变,该回旋加速器可以加速质子
B.仅将磁场的磁感应强度变为2倍,该回旋加速器仍可加速粒子
C.保持B和T不变,该回旋加速器可以加速粒子(电荷量为质子
的2倍,质量为质子的4倍),加速后粒子的最大动能是粒子最大动能的2倍
D.保持B和T不变,该回旋加速器可以加速粒子(电荷量为质子的2倍,质量
为质子的4倍),且粒子在回旋加速器中运动的时间与粒子的运动时间相等
CD
5.回旋加速器是用来加速一群带电粒子使它们获得很大动能的仪器,其核心部分是两个D形金属盒,两盒分别和一高频交流电源两极相接,以便在盒内的窄缝中形成匀强电场,使粒子每次穿过窄缝时都能被加速,加速电压大小始终为U,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为Rmax。求:
(1)所加交流电源频率;
(2)粒子离开加速器时的最大动能;
(3)粒子被加速次数;
(4)若带电粒子在电场中加速的加速度大小恒为a,粒子在电场中加速的总时间。
一、质谱仪
由:
得:
二、回旋加速器
1.条件:
2.粒子能量:
=
1.4 质谱仪与回旋加速器
怎么分开电荷量相同,但质量不同的带电粒子?
质谱仪
阿斯顿
一、质谱仪
一、质谱仪
粒子源
加速电场U
偏转磁场B
照相底片
2.原理:
在电场中加速
在磁场中偏转
质谱线或谱线
则比荷
质量
3.用途:
1.构造:
测量带电粒子的比荷、质量;
分析同位素
1.(多选)利用质谱仪可以分析碘的各种同位素。如图所示,电荷量相同的带正电的131I与127I从容器A下方的小孔S1进入加速电场(初速度不计),经电场加速后从小孔S2射出,进入垂直纸面的匀强磁场中,最后打在照相底片D上。下列说法正确的是( )
A.磁场的方向垂直纸面向里
B.打在b处的是127I
C.127I在磁场中运动速度更大
D.131I在磁场中运动时间更长
CD
2.质谱仪的原理图如图所示,由加速电场、速度选择器和偏转磁场组成。在速度选择器中存在相互垂直的匀强电场和匀强磁场(图中未画出)。偏转磁场是一个以直线MN为边界、方向垂直纸面向外、磁感应强度大小为B2的匀强磁场。一电荷量为q、质量为m的带正电的粒子从静止开始经过加速电场后,进入速度选择器,并能沿直线穿过速度选择器,从A点垂直MN进入偏转磁场。带电粒子经偏转磁场后,最终到达照相底片的C点。已知速度选择器中的电场方向水平向右、电场强度大小为E,A点到C点的距离为x,
带电粒子所受的重力可忽略不计。求:
(1)粒子进入偏转磁场的速度大小v;
(2)速度选择器中匀强磁场的磁感应强度B1的大小和方向;
(3)加速电场的电势差U。
直线加速器
0
1
2
3
4
5
6
7
8
交变电压
加速电场
斯坦福大学加速器
北京正负电子对撞机
直线加速器占地空间非常大,有的长达几十千米,坐落在两个城市之间
欧内斯特·劳伦斯与他自己发明的回旋加速器
二、回旋加速器
二、回旋加速器
1.构造:
二、回旋加速器
1.构造:
2.原理:
(1)粒子经电场加速,经磁场回旋
(2)加速条件:
交流电源的周期等于粒子做圆周运动的周期
一个周期内,粒子加速 次
二、回旋加速器
1.构造:
2.原理:
(3)最大动能:
若D形盒半径为R
对某种粒子q、m一定,粒子获得的最大动能由磁感应强度B和回旋加速器的半径R决定,与加速度电压的大小无关。
二、回旋加速器
1.构造:
2.原理:
(4)加速次数:
(5)运动时间:
加速时间:
回旋时间:
回旋加速器不可无限加速。
粒子速度v接近光速c时,质量变大,在磁场中运动周期改变,与交变电场周期不同步。
只要不断增大回旋加速器的半径R,就能不断提高粒子获得的速度吗?
实际上,回旋加速器加速的带电粒子,能量达到25~30MeV后,就很难再加速了
3.某小型医用回旋加速器,最大回旋半径为0.5 m,磁感应强度大小为1.12 T,质子加速后获得的最大动能为1.5×107 eV。根据给出的数据,可计算质子经该回旋加速器加速后的最大速率约为( )
(忽略相对论效应,1 eV=1.6×10-19 J)
A.3.6×106 m/s B.1.2×107 m/s
C.5.4×107 m/s D.2.4×108 m/s
C
4.(多选)如图所示为回旋加速器示意图,利用回旋加速器对粒子(电荷量和质子相等,质量为质子的2倍)进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T。忽略粒子在D形盒缝隙间的运动时间和相对论效应,下列说法正确的是( )
A.保持B和T不变,该回旋加速器可以加速质子
B.仅将磁场的磁感应强度变为2倍,该回旋加速器仍可加速粒子
C.保持B和T不变,该回旋加速器可以加速粒子(电荷量为质子
的2倍,质量为质子的4倍),加速后粒子的最大动能是粒子最大动能的2倍
D.保持B和T不变,该回旋加速器可以加速粒子(电荷量为质子的2倍,质量
为质子的4倍),且粒子在回旋加速器中运动的时间与粒子的运动时间相等
CD
5.回旋加速器是用来加速一群带电粒子使它们获得很大动能的仪器,其核心部分是两个D形金属盒,两盒分别和一高频交流电源两极相接,以便在盒内的窄缝中形成匀强电场,使粒子每次穿过窄缝时都能被加速,加速电压大小始终为U,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为Rmax。求:
(1)所加交流电源频率;
(2)粒子离开加速器时的最大动能;
(3)粒子被加速次数;
(4)若带电粒子在电场中加速的加速度大小恒为a,粒子在电场中加速的总时间。
一、质谱仪
由:
得:
二、回旋加速器
1.条件:
2.粒子能量:
=
