人教版数学八年级下18.1.2平行四边形的判定课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下18.1.2平行四边形的判定课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-14 12:44:30 | ||
图片预览


文档简介
课件21张PPT。
18.1.2平行四边形的判定温故而知新 1、平行四边形的定义是什么?有什么作用?2、平行四边形有哪些性质?平行四边形的对边相等.
平行四边形的对角相等.平行四边形的对角线互相
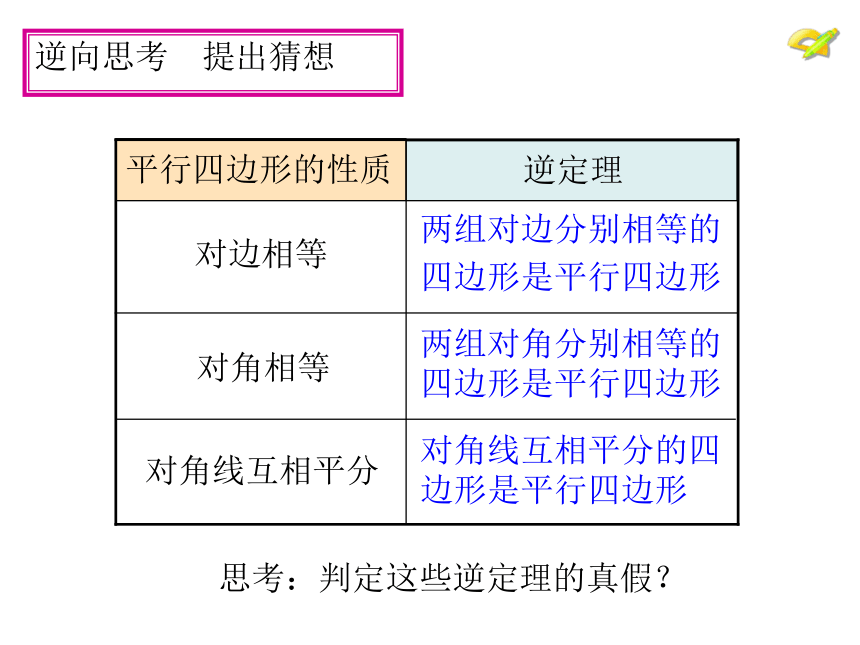
平分.逆向思考 提出猜想 两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
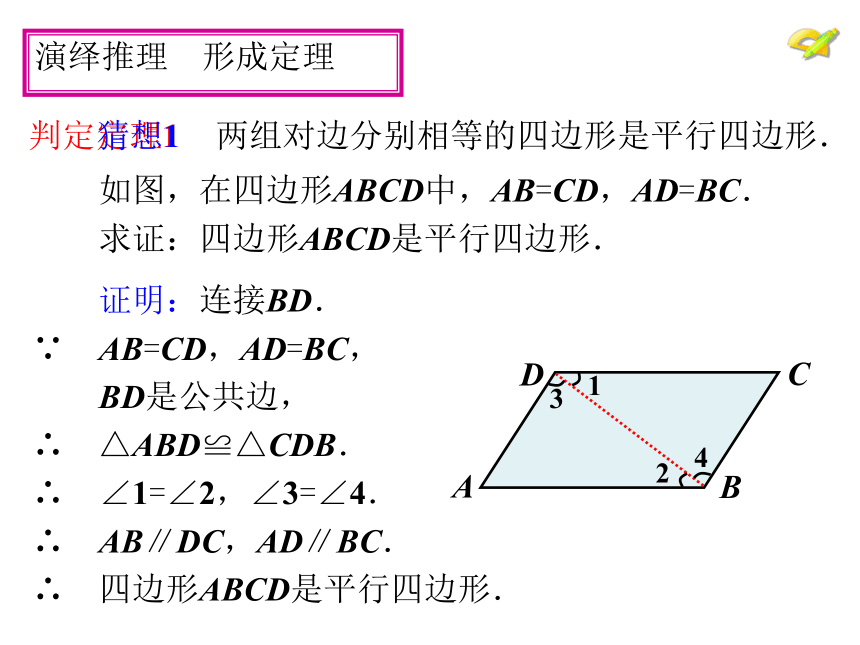
边形是平行四边形 思考:判定这些逆定理的真假? 证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对边分别相等的四边形是平行四边形. 判定定理1 猜想1 ∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
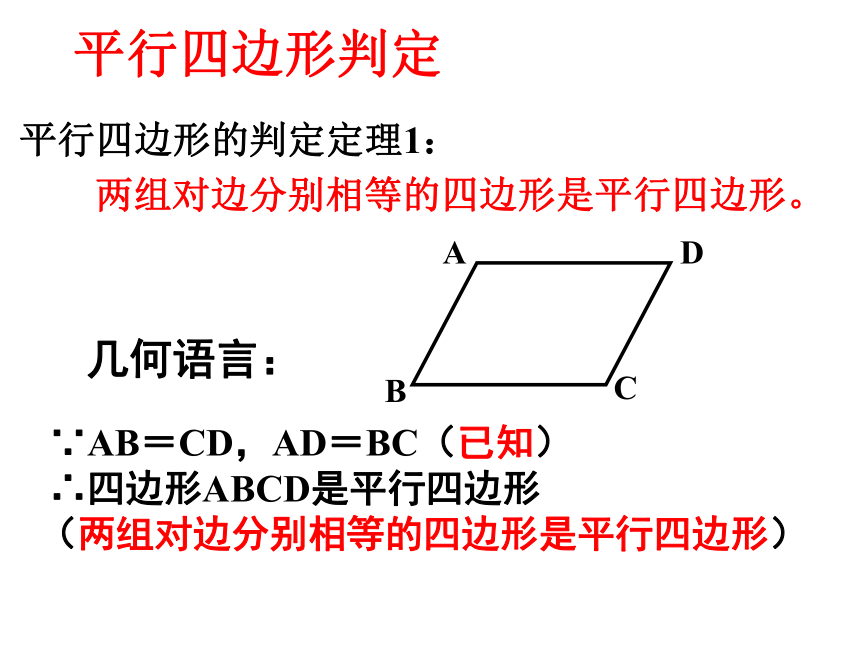
(两组对边分别相等的四边形是平行四边形) 平行四边形判定平行四边形的判定定理1:
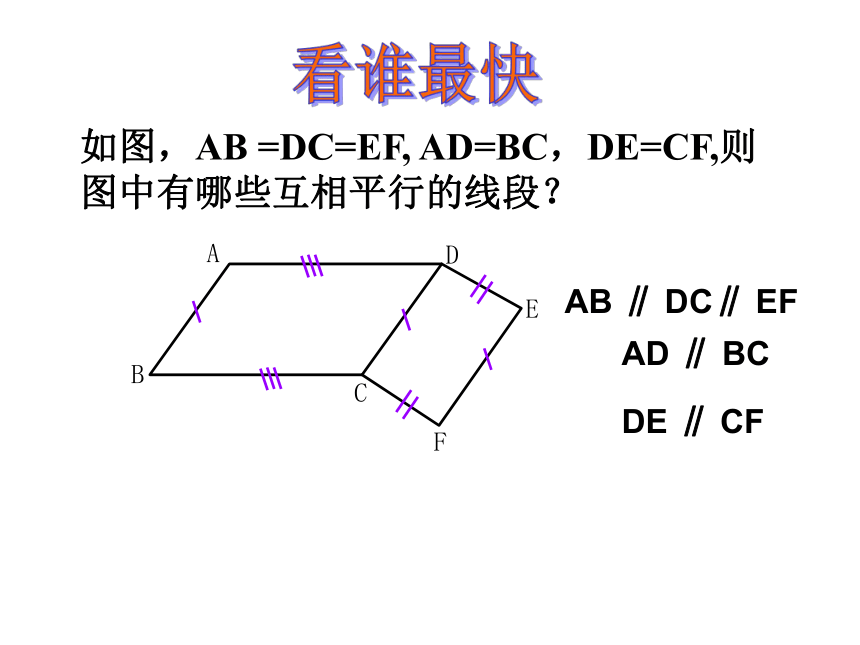
两组对边分别相等的四边形是平行四边形。几何语言:如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 如图,在四边形ABCD中,AC,BD相交于点O,且
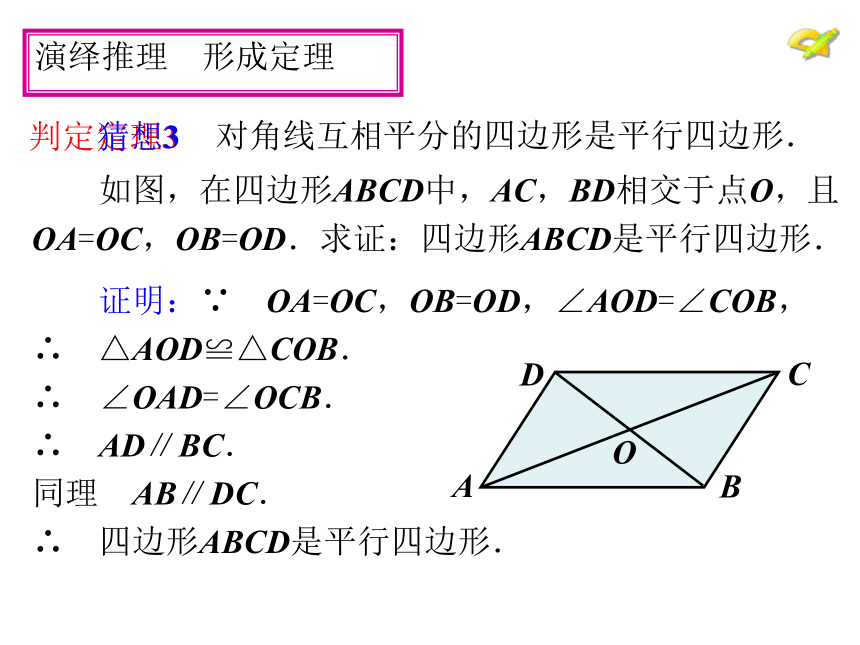
OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 演绎推理 形成定理 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
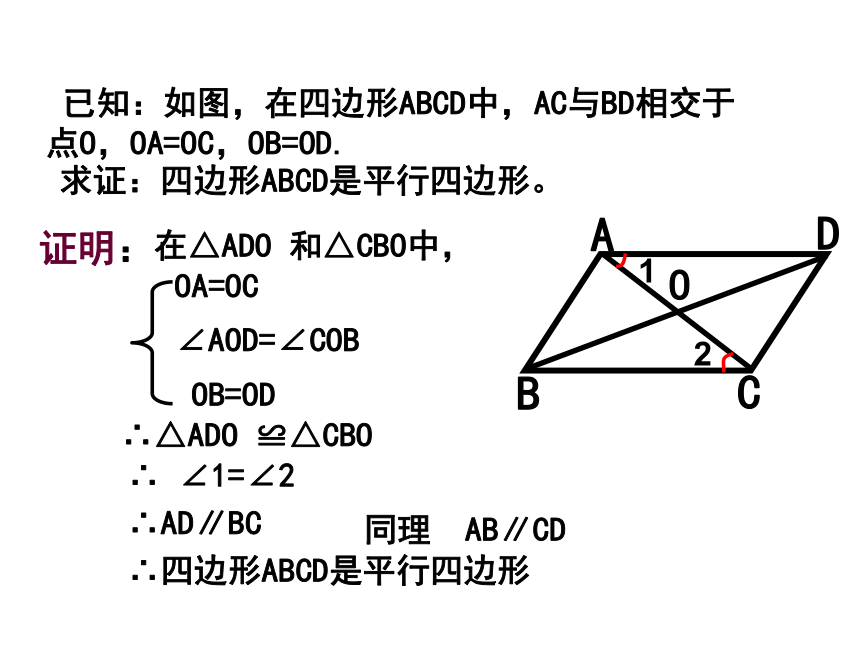
∴ 四边形ABCD是平行四边形. 已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.∴△ADO ≌△CBO OA=OC 证明: OB=OD∠AOD=∠COB∴四边形ABCD是平行四边形求证:四边形ABCD是平行四边形。O21在△ADO 和△CBO中,∴ ∠1=∠2 ∴AD∥BC同理 AB∥CD对角线互相平分的四边形是平行四边形。几何语言:∵OA=OC OB=OD∴四边形ABCD是平行四边形。(对角线互相平分的四边形是平行四边形) 请你识别下列四边形哪些是平行四边形?请说明理由?(1)(3)
(2)BADC4.8㎝4.8㎝7.6㎝7.6㎝夯实基础 平行四边形的判定定理:
1、两组对边分别相等的四边形是平行四边形。两组对角分别相等的四边形是平行四边形。对角线互相平分的四边形是平行四边形。2、3、复习灵活运用 掌握知识 O 例 如图:平行四边形ABCD的对角线AC、BD相交
于点O,点E,F 分别在AC 两侧的延长线上,并
且AE=CF. 求证: 四边形BFDE是平行四边形。
例3 如图:平行四边形ABCD的对角线AC、BD相交 于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。范例赏析你还有其他的证明方法吗? 证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
创设情境:四边形ABCD是平行四边形猜测:一组对边平行且相等的四边形是平行四边形 已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行四边形证明:连接BD∵ AB∥CD∴∠ABD = ∠CDB又∵AB =CD ,BD = DB∴△ABD ≌△CDB (SAS)∴AD = CB∴四边形ABCD是平行四边形又∵AB =CD 符号语言:判定方法一组对边平行且相等的四边形是平行四边形 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.基础练习 例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.基础练习 例2 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.(P50 6题)两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形. 课堂小结 判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法? 综合运用 例3 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
平行四边形的对角相等.平行四边形的对角线互相
平分.逆向思考 提出猜想 两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
边形是平行四边形 思考:判定这些逆定理的真假? 证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对边分别相等的四边形是平行四边形. 判定定理1 猜想1 ∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形) 平行四边形判定平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。几何语言:如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 演绎推理 形成定理 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形. 已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.∴△ADO ≌△CBO OA=OC 证明: OB=OD∠AOD=∠COB∴四边形ABCD是平行四边形求证:四边形ABCD是平行四边形。O21在△ADO 和△CBO中,∴ ∠1=∠2 ∴AD∥BC同理 AB∥CD对角线互相平分的四边形是平行四边形。几何语言:∵OA=OC OB=OD∴四边形ABCD是平行四边形。(对角线互相平分的四边形是平行四边形) 请你识别下列四边形哪些是平行四边形?请说明理由?(1)(3)
(2)BADC4.8㎝4.8㎝7.6㎝7.6㎝夯实基础 平行四边形的判定定理:
1、两组对边分别相等的四边形是平行四边形。两组对角分别相等的四边形是平行四边形。对角线互相平分的四边形是平行四边形。2、3、复习灵活运用 掌握知识 O 例 如图:平行四边形ABCD的对角线AC、BD相交
于点O,点E,F 分别在AC 两侧的延长线上,并
且AE=CF. 求证: 四边形BFDE是平行四边形。
例3 如图:平行四边形ABCD的对角线AC、BD相交 于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。范例赏析你还有其他的证明方法吗? 证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
创设情境:四边形ABCD是平行四边形猜测:一组对边平行且相等的四边形是平行四边形 已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行四边形证明:连接BD∵ AB∥CD∴∠ABD = ∠CDB又∵AB =CD ,BD = DB∴△ABD ≌△CDB (SAS)∴AD = CB∴四边形ABCD是平行四边形又∵AB =CD 符号语言:判定方法一组对边平行且相等的四边形是平行四边形 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.基础练习 例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.基础练习 例2 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.(P50 6题)两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形. 课堂小结 判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法? 综合运用 例3 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
