人教版数学九上第二十四章 圆 单元试卷(含答案)
文档属性
| 名称 | 人教版数学九上第二十四章 圆 单元试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 971.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 17:37:27 | ||
图片预览

文档简介
人教版数学九上第二十四章圆单元试卷
一、单选题
1.的半径为r,点P到圆心O的距离为2,若点P在外,则( )
A. B. C. D.
2.下列说法正确的是( )
A.弦是直径 B.平分弦的直径垂直于弦
C.优弧一定大于劣弧 D.在同圆或等圆中,等弧所对的圆心角相等
3.用反证法证明命题“在中,若,则”时,首先应假设( )
A. B. C. D.
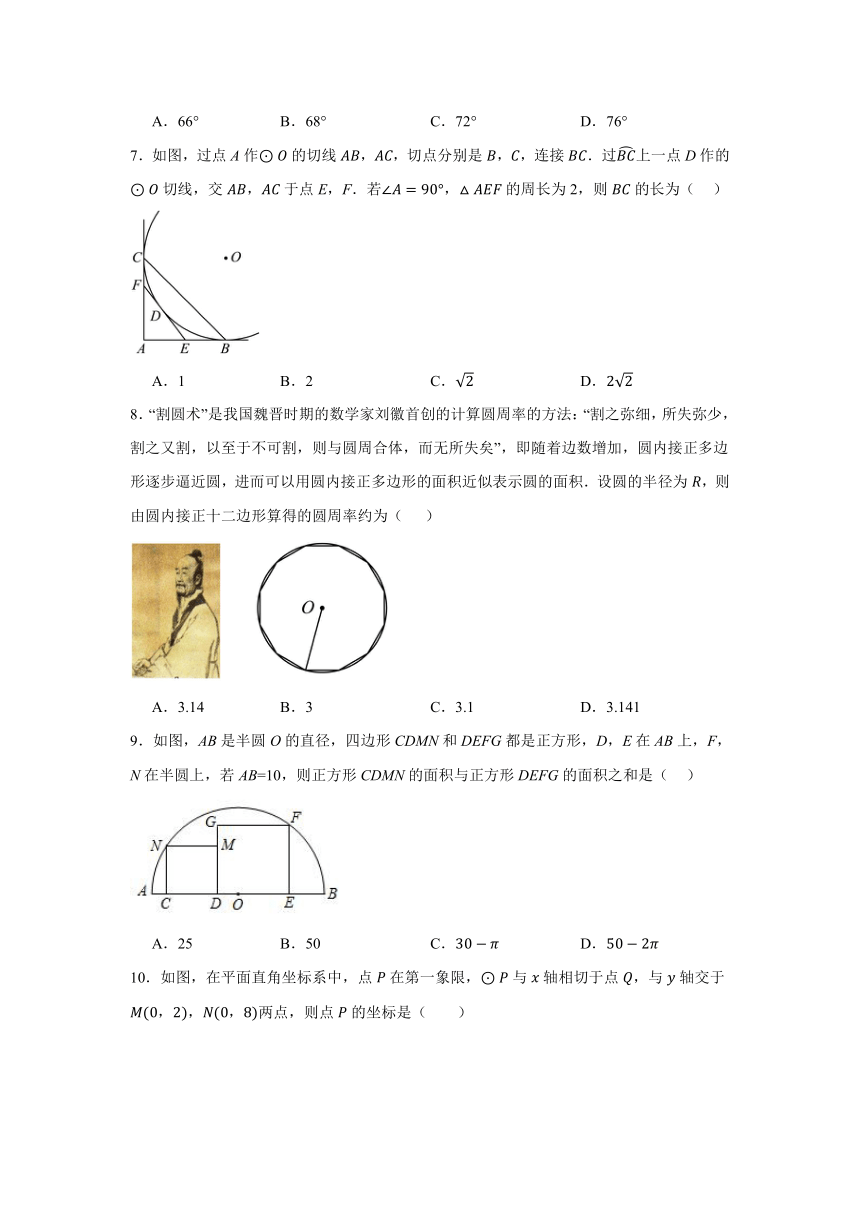
4.如图,A、B、C是上的三点, ,则等于( )
A. B. C. D.
5.如图,正六边形内接于,半径为,则这个正六边形的边心距的长为( )
A. B. C. D.
6.如图,圆中,,过点A作的平行线交过点C的圆的切线于点D,若,则的度数是( )
A.66° B.68° C.72° D.76°
7.如图,过点A作的切线,,切点分别是,,连接.过上一点D作的切线,交,于点E,F.若,的周长为2,则的长为( )
A.1 B.2 C. D.
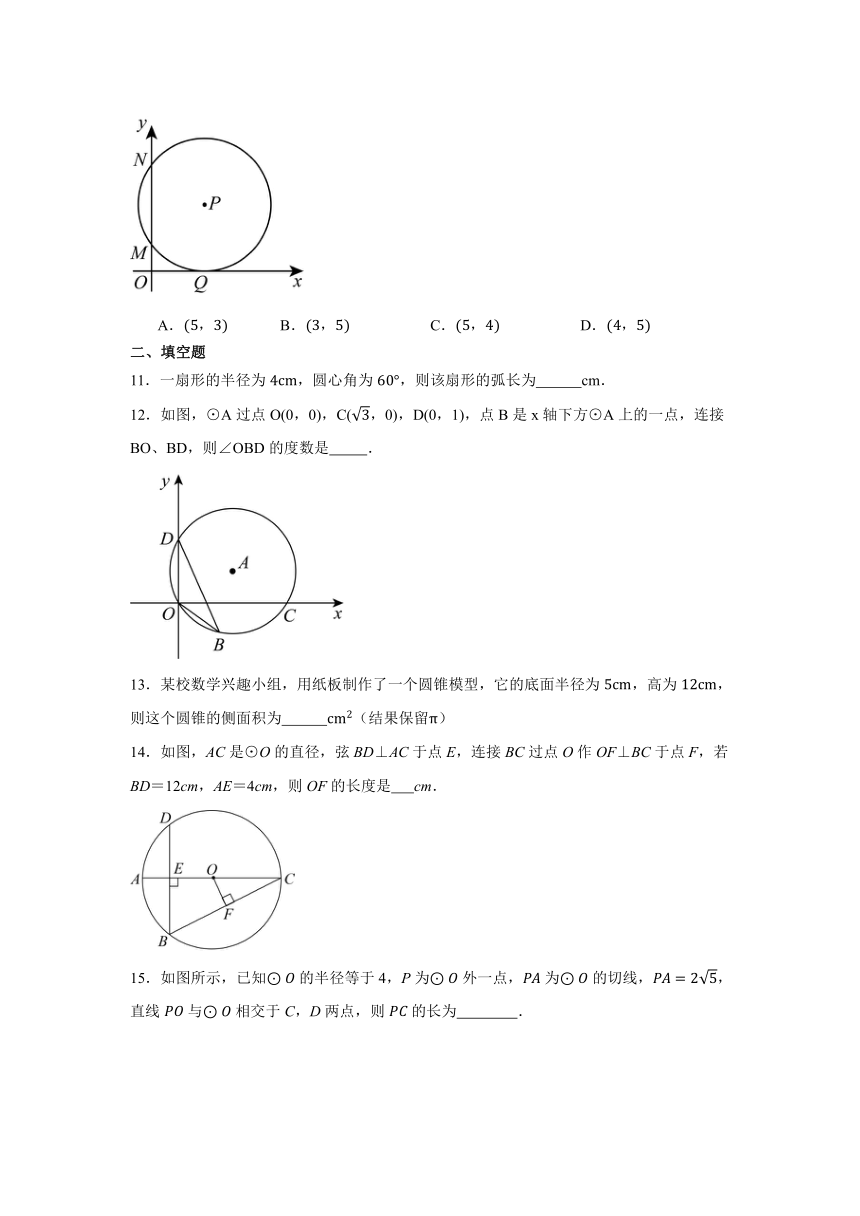
8.“割圆术”是我国魏晋时期的数学家刘徽首创的计算圆周率的方法:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即随着边数增加,圆内接正多边形逐步逼近圆,进而可以用圆内接正多边形的面积近似表示圆的面积.设圆的半径为,则由圆内接正十二边形算得的圆周率约为( )
A.3.14 B.3 C.3.1 D.3.141
9.如图,AB是半圆O的直径,四边形CDMN和DEFG都是正方形,D,E在AB上,F,N在半圆上,若AB=10,则正方形CDMN的面积与正方形DEFG的面积之和是( )
A.25 B.50 C. D.
10.如图,在平面直角坐标系中,点在第一象限,与轴相切于点,与轴交于,两点,则点的坐标是( )
A. B. C. D.
二、填空题
11.一扇形的半径为,圆心角为,则该扇形的弧长为 cm.
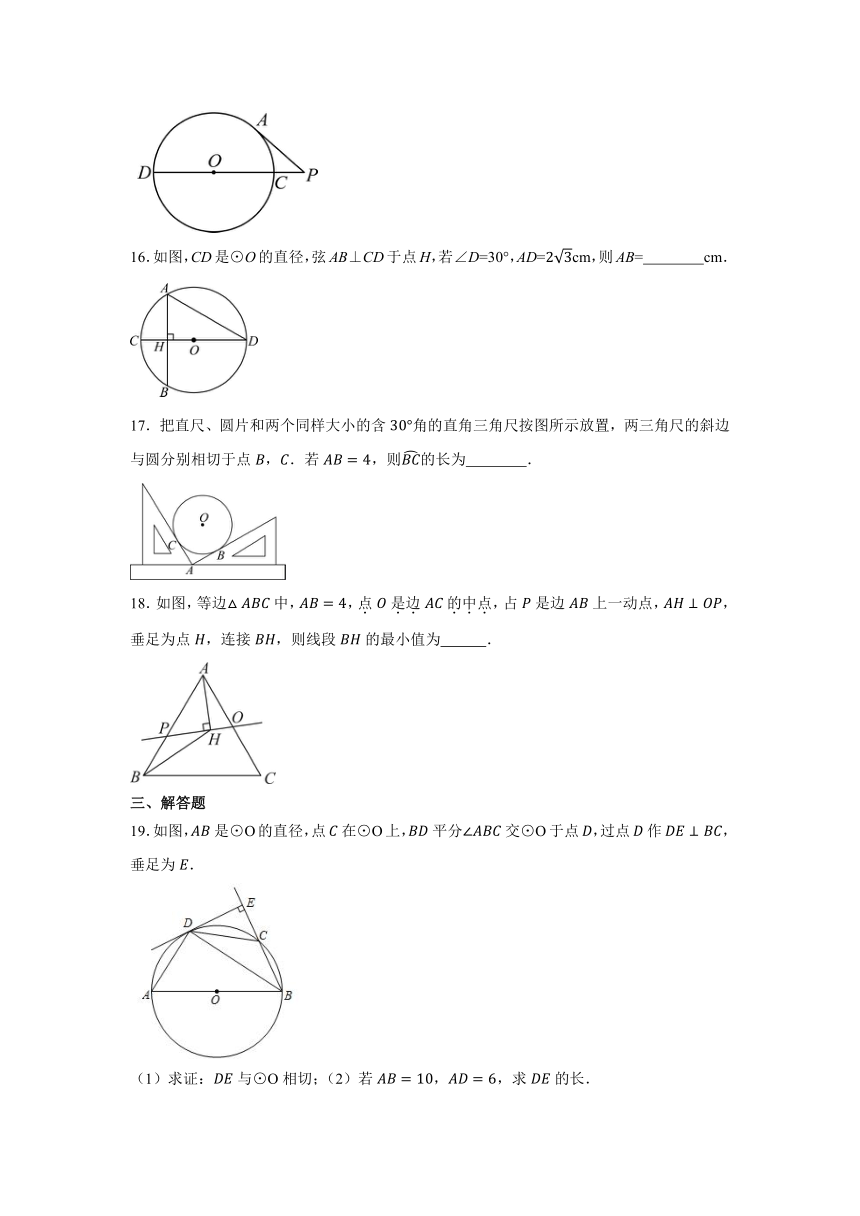
12.如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO、BD,则∠OBD的度数是 .
13.某校数学兴趣小组,用纸板制作了一个圆锥模型,它的底面半径为,高为,则这个圆锥的侧面积为 (结果保留)
14.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
15.如图所示,已知的半径等于4,P为外一点,为的切线,,直线与相交于C,D两点,则的长为 .
16.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,AD=cm,则AB= cm.
17.把直尺、圆片和两个同样大小的含角的直角三角尺按图所示放置,两三角尺的斜边与圆分别相切于点,.若,则的长为 .
18.如图,等边中,,点是边的中点,占是边上一动点,,垂足为点,连接,则线段的最小值为 .
三、解答题
19.如图,是⊙O的直径,点在⊙O上,平分交⊙O于点,过点作,垂足为.
(1)求证:与⊙O相切;(2)若,,求的长.
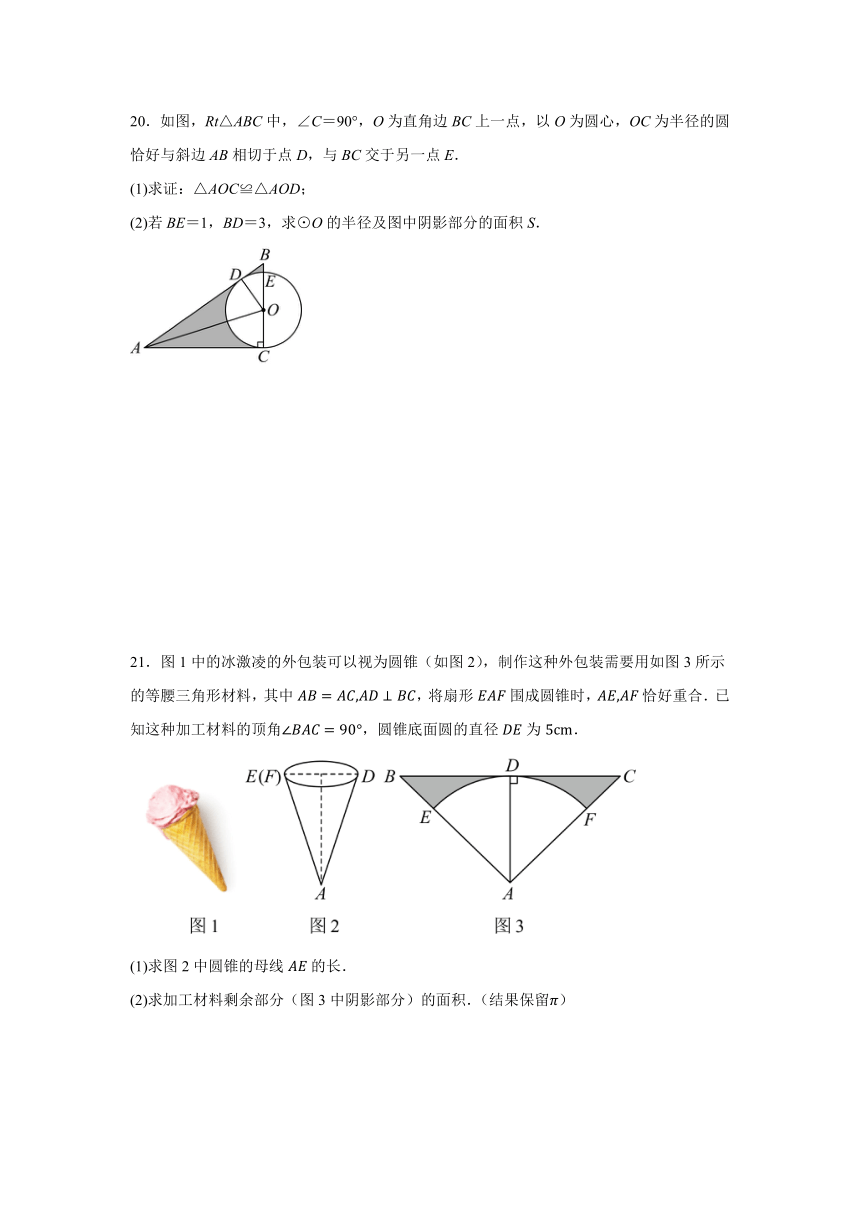
20.如图,Rt△ABC中,∠C=90°,O为直角边BC上一点,以O为圆心,OC为半径的圆恰好与斜边AB相切于点D,与BC交于另一点E.
(1)求证:△AOC≌△AOD;
(2)若BE=1,BD=3,求⊙O的半径及图中阴影部分的面积S.
21.图1中的冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形围成圆锥时,恰好重合.已知这种加工材料的顶角,圆锥底面圆的直径为.
(1)求图2中圆锥的母线的长.
(2)求加工材料剩余部分(图3中阴影部分)的面积.(结果保留)
22.如图是北京地坛公园景区的圆弧形门,张红同学元旦节日和妈妈到景区游玩,她很想知道这扇门的相关数据,于是她从景区管理人员处了解到:这个圆弧形门所在的圆与水平地面是相切的..且与水平地面都是垂直的,根据以上数据,请你帮助张红同学计算出这个圆弧形门的最高点离地面的高度是多少?
23.图1是传统的手工推磨工具,根据它的原理设计了如图2所示的机械设备,磨盘半径,用长为的连杆将点Q与动力装置P相连(大小可变),点P在轨道上滑动,并带动磨盘绕点O转动,,.
(1)如图2,当与相切时,求的长.
(2)在磨盘转动过程中,求的最大值及最小值
24.如图,有一座圆弧形拱桥,它的跨度为,拱高为,当洪水泛滥到跨度只有时,就要采取紧急措施.
(1)求拱桥所在圆的半径;
(2)若某次洪水中,拱顶离水面只有,即,通过计算说明是否需要采取紧急措施.
25.综合与实践【数学理解】德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图2,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大.人们称这一命题为米勒定理.
(1)【问题提出】如图1,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
(2)【问题解决】如图3,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆⊙与轴相切于点时,最大.当最大时,求点的坐标.
参考答案:
1.A
2.D
3.D
4.B
5.B
6.A
7.C
8.B
9.A
10.D
11.
12.30°
13.
14..
15.2
16.
17.
18.
19.(1)证明:连接.
∵,∴.
∵平分,∴.
∴,∴.
∴.
∵,∴.
∴.∴.
∴与相切;
(2)过作于.
∵平分,,∴.
∵,∴.
∴,∴.
∵是的直径,∴.
∵,,
∴.
∵,∴.
∴.
20.(1)证明:∵D是切点
∴OD⊥AB
∴△OAD是Rt△
∴在Rt△OAD和Rt△OAC中
OD=OC,AO=AO
∴△AOD≌△AOC
(2) ∵在Rt△OBD中,OD=
设半径为r,则有:
∴
∵AD、AC是⊙O的切线
∴AD=AC
令AD=AC=x 则有:
∴S△ABC=
S半圆=
21.(1)解:根据题意得,
,
∴;
(2)解:,,,
而,
,
.
22.解:设为切点,连接,交于点,
是的切线,为半径,
,
四边形是矩形,
,
厘米米,厘米米,
设圆的半径为,在中,
米,
,
,
,
解得:,
(米).
答:这扇圆弧形门的最高点离地面的距离是2.5米.
23.(1)连接,如图2,
∵与相切,
∴,
在中,
∴,
在中,;
(2)如图3,当运动到时,点运动在上距离点最远,
在中,,,
∴,
当运动到时,点运动在上距离点最近,
在中,,,
∴.
24.(1)解:设拱桥所在圆的圆心为,连接,如下图,
由题意易知,点共线,且,则,
设拱桥所在圆的半径为,则,
在中,,
由勾股定理,可得,即,
解得,
所以,拱桥所在圆的半径为;
(2)连接,如图,
由(1)知,
∴,
∵,,
∴,
∴,
在中,由勾股定理,得,
∴,
∴不需要采取紧急措施.
25.1)证明:由图可知:∵,是所对的圆周角,
∴,
∵,
∴,
∴.
(2)当的外接圆⊙与轴相切于点时,最大,
∴连接,,过点作于点,
∴四边形是矩形,
∴,,
∵,,
∴,
∴在中,,
∵点,的坐标分别是,,
∴,,
∴,,
∴,
∴,
∴点.
一、单选题
1.的半径为r,点P到圆心O的距离为2,若点P在外,则( )
A. B. C. D.
2.下列说法正确的是( )
A.弦是直径 B.平分弦的直径垂直于弦
C.优弧一定大于劣弧 D.在同圆或等圆中,等弧所对的圆心角相等
3.用反证法证明命题“在中,若,则”时,首先应假设( )
A. B. C. D.
4.如图,A、B、C是上的三点, ,则等于( )
A. B. C. D.
5.如图,正六边形内接于,半径为,则这个正六边形的边心距的长为( )
A. B. C. D.
6.如图,圆中,,过点A作的平行线交过点C的圆的切线于点D,若,则的度数是( )
A.66° B.68° C.72° D.76°
7.如图,过点A作的切线,,切点分别是,,连接.过上一点D作的切线,交,于点E,F.若,的周长为2,则的长为( )
A.1 B.2 C. D.
8.“割圆术”是我国魏晋时期的数学家刘徽首创的计算圆周率的方法:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即随着边数增加,圆内接正多边形逐步逼近圆,进而可以用圆内接正多边形的面积近似表示圆的面积.设圆的半径为,则由圆内接正十二边形算得的圆周率约为( )
A.3.14 B.3 C.3.1 D.3.141
9.如图,AB是半圆O的直径,四边形CDMN和DEFG都是正方形,D,E在AB上,F,N在半圆上,若AB=10,则正方形CDMN的面积与正方形DEFG的面积之和是( )
A.25 B.50 C. D.
10.如图,在平面直角坐标系中,点在第一象限,与轴相切于点,与轴交于,两点,则点的坐标是( )
A. B. C. D.
二、填空题
11.一扇形的半径为,圆心角为,则该扇形的弧长为 cm.
12.如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO、BD,则∠OBD的度数是 .
13.某校数学兴趣小组,用纸板制作了一个圆锥模型,它的底面半径为,高为,则这个圆锥的侧面积为 (结果保留)
14.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
15.如图所示,已知的半径等于4,P为外一点,为的切线,,直线与相交于C,D两点,则的长为 .
16.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,AD=cm,则AB= cm.
17.把直尺、圆片和两个同样大小的含角的直角三角尺按图所示放置,两三角尺的斜边与圆分别相切于点,.若,则的长为 .
18.如图,等边中,,点是边的中点,占是边上一动点,,垂足为点,连接,则线段的最小值为 .
三、解答题
19.如图,是⊙O的直径,点在⊙O上,平分交⊙O于点,过点作,垂足为.
(1)求证:与⊙O相切;(2)若,,求的长.
20.如图,Rt△ABC中,∠C=90°,O为直角边BC上一点,以O为圆心,OC为半径的圆恰好与斜边AB相切于点D,与BC交于另一点E.
(1)求证:△AOC≌△AOD;
(2)若BE=1,BD=3,求⊙O的半径及图中阴影部分的面积S.
21.图1中的冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形围成圆锥时,恰好重合.已知这种加工材料的顶角,圆锥底面圆的直径为.
(1)求图2中圆锥的母线的长.
(2)求加工材料剩余部分(图3中阴影部分)的面积.(结果保留)
22.如图是北京地坛公园景区的圆弧形门,张红同学元旦节日和妈妈到景区游玩,她很想知道这扇门的相关数据,于是她从景区管理人员处了解到:这个圆弧形门所在的圆与水平地面是相切的..且与水平地面都是垂直的,根据以上数据,请你帮助张红同学计算出这个圆弧形门的最高点离地面的高度是多少?
23.图1是传统的手工推磨工具,根据它的原理设计了如图2所示的机械设备,磨盘半径,用长为的连杆将点Q与动力装置P相连(大小可变),点P在轨道上滑动,并带动磨盘绕点O转动,,.
(1)如图2,当与相切时,求的长.
(2)在磨盘转动过程中,求的最大值及最小值
24.如图,有一座圆弧形拱桥,它的跨度为,拱高为,当洪水泛滥到跨度只有时,就要采取紧急措施.
(1)求拱桥所在圆的半径;
(2)若某次洪水中,拱顶离水面只有,即,通过计算说明是否需要采取紧急措施.
25.综合与实践【数学理解】德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图2,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大.人们称这一命题为米勒定理.
(1)【问题提出】如图1,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
(2)【问题解决】如图3,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆⊙与轴相切于点时,最大.当最大时,求点的坐标.
参考答案:
1.A
2.D
3.D
4.B
5.B
6.A
7.C
8.B
9.A
10.D
11.
12.30°
13.
14..
15.2
16.
17.
18.
19.(1)证明:连接.
∵,∴.
∵平分,∴.
∴,∴.
∴.
∵,∴.
∴.∴.
∴与相切;
(2)过作于.
∵平分,,∴.
∵,∴.
∴,∴.
∵是的直径,∴.
∵,,
∴.
∵,∴.
∴.
20.(1)证明:∵D是切点
∴OD⊥AB
∴△OAD是Rt△
∴在Rt△OAD和Rt△OAC中
OD=OC,AO=AO
∴△AOD≌△AOC
(2) ∵在Rt△OBD中,OD=
设半径为r,则有:
∴
∵AD、AC是⊙O的切线
∴AD=AC
令AD=AC=x 则有:
∴S△ABC=
S半圆=
21.(1)解:根据题意得,
,
∴;
(2)解:,,,
而,
,
.
22.解:设为切点,连接,交于点,
是的切线,为半径,
,
四边形是矩形,
,
厘米米,厘米米,
设圆的半径为,在中,
米,
,
,
,
解得:,
(米).
答:这扇圆弧形门的最高点离地面的距离是2.5米.
23.(1)连接,如图2,
∵与相切,
∴,
在中,
∴,
在中,;
(2)如图3,当运动到时,点运动在上距离点最远,
在中,,,
∴,
当运动到时,点运动在上距离点最近,
在中,,,
∴.
24.(1)解:设拱桥所在圆的圆心为,连接,如下图,
由题意易知,点共线,且,则,
设拱桥所在圆的半径为,则,
在中,,
由勾股定理,可得,即,
解得,
所以,拱桥所在圆的半径为;
(2)连接,如图,
由(1)知,
∴,
∵,,
∴,
∴,
在中,由勾股定理,得,
∴,
∴不需要采取紧急措施.
25.1)证明:由图可知:∵,是所对的圆周角,
∴,
∵,
∴,
∴.
(2)当的外接圆⊙与轴相切于点时,最大,
∴连接,,过点作于点,
∴四边形是矩形,
∴,,
∵,,
∴,
∴在中,,
∵点,的坐标分别是,,
∴,,
∴,,
∴,
∴,
∴点.
同课章节目录
