7.5 正态分布 教学设计
文档属性
| 名称 | 7.5 正态分布 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 10:13:56 | ||
图片预览

文档简介
正态分布
教学目标:
1.知识与技能
① 通过高尔顿板试验,了解正态分布密度曲线的来源
② 通过借助几何画板,理解正态分布的概念及其曲线特点,掌握利用原则解决一些简单的与正态分布有关的概率计算问题
2.过程与方法
① 通过试验、频率分布直方图、几何画板操作认识正态曲线,体验从有限到无限的思想方法
② 通过观察正态曲线研究正态曲线的性质,体会数形结合的方法,增强观察、分析和归纳的能力
3、情感态度与价值观
① 通过经历直观动态的高尔顿试验,提高学习数学的兴趣
② 通过联系实际,让学生发现现实生活中有哪些例子服从或近似服从正态分布,是学生认识到数学知识来源于生活、服务于生活
③通过原则的学习,充分感受数学的对称美
教学重点、难点
重点:正态分布密度曲线的特点,利用原则解决一些简单的与正态分布有关的概率计算问题
难点:正态分布密度曲线的特点
教学过程:
创设情境
首先通过高尔顿板实验向学生演示了小球落下的规律。
具体操作如下:自上端放入一小球,任其自由下落,在下落过程中小球碰到下一排钉子,最后落入底板中的某个格。因此任意放入一个球,小球最后落入某个格子内事先是难以确定的,但是实验证明,如果放入大量球的话则其最后呈现的曲线总是雷同的,也就是说落入格中的小球的频率趋向稳定。
给学生演示操作,让学生更直观地看到小球动态的落入情况,提高了学生的学习兴趣。
随着实验重复次数的增加,频率直方图的形状会越来越像一条钟形曲线。
新课讲授
(1)正态曲线
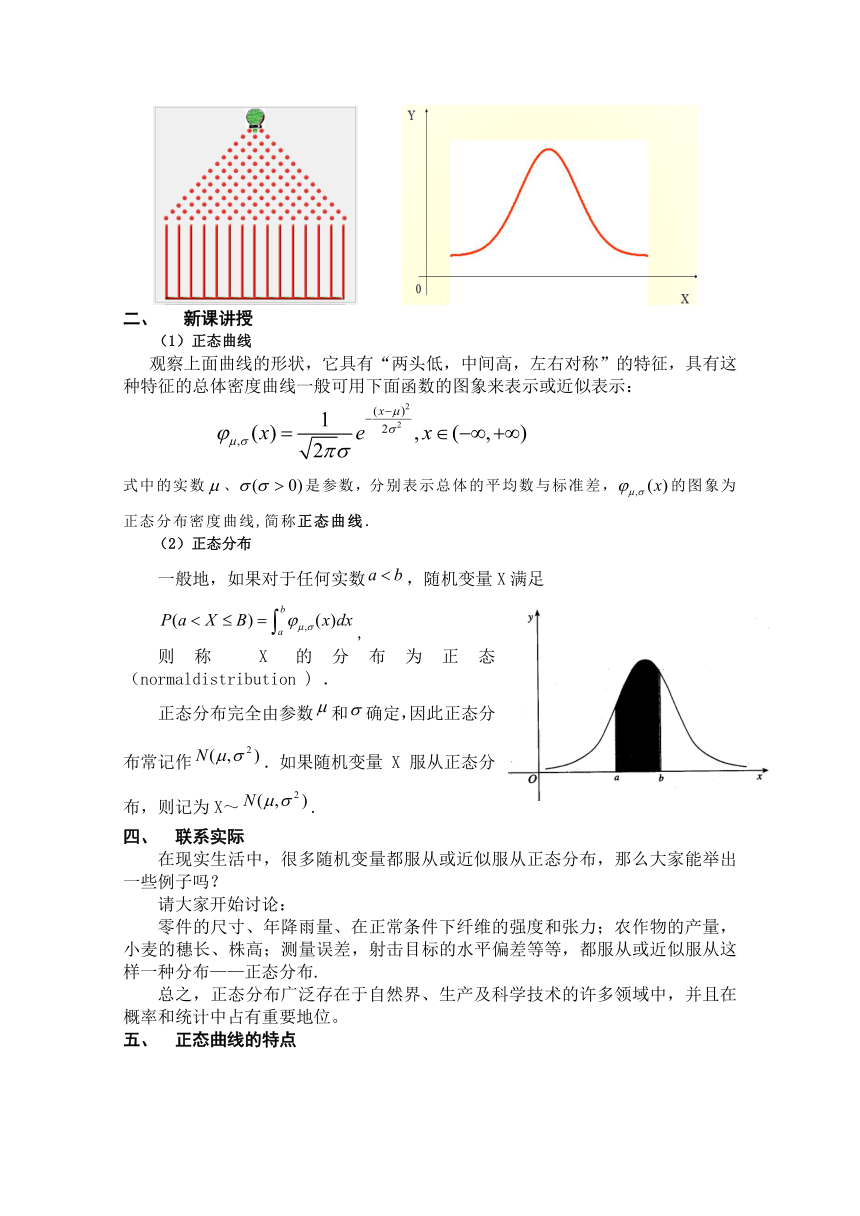
观察上面曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:
式中的实数、是参数,分别表示总体的平均数与标准差,的图象为正态分布密度曲线,简称正态曲线.
(2)正态分布
一般地,如果对于任何实数,随机变量X满足
,
则称 X 的分布为正态(normaldistribution ) .
正态分布完全由参数和确定,因此正态分布常记作.如果随机变量 X 服从正态分布,则记为X~.
联系实际
在现实生活中,很多随机变量都服从或近似服从正态分布,那么大家能举出一些例子吗?
请大家开始讨论:
零件的尺寸、年降雨量、在正常条件下纤维的强度和张力;农作物的产量,小麦的穗长、株高;测量误差,射击目标的水平偏差等等,都服从或近似服从这样一种分布——正态分布.
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中,并且在概率和统计中占有重要地位。
正态曲线的特点
(1)曲线在x轴的上方,与x轴不相交
(2)曲线关于直线x=μ对称
(3)当x=μ时,曲线位于最高点
(4)曲线与x轴之间的面积为1
通过几何画板的演示:
学生又得出两个性质:
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
特殊区间的概率
若~,则对于任何实数,
为图中阴影部分的面积
对于固定的和a而言,该面积随着的减少而变化,这说明越小,X落在区间的概率越大,即X集中在周围概率越大。
特别有:
上述结果可用下图表示:
可以看到,正态总体几乎总取值于区间之内,而在此区间以外取值的概率只有0.0026,通常认为这种情况在一次试验中几乎不可能发生。在实际应用中就只考虑这个区间,称为原则.
例题分析
把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
课堂小结
了解正态曲线、正态分布的概念,
知道正态曲线的解析式及曲线的特点。
3. 能够结合现实理解正态分布在现实生活中的应用。
教学反思
在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布
板书设计
正态分布
解析式曲线性质 ⑴ ⑵ ⑶ ⑷ ⑸3.3原则 例1. 例2①②③④ 例3 多媒体投影
教学目标:
1.知识与技能
① 通过高尔顿板试验,了解正态分布密度曲线的来源
② 通过借助几何画板,理解正态分布的概念及其曲线特点,掌握利用原则解决一些简单的与正态分布有关的概率计算问题
2.过程与方法
① 通过试验、频率分布直方图、几何画板操作认识正态曲线,体验从有限到无限的思想方法
② 通过观察正态曲线研究正态曲线的性质,体会数形结合的方法,增强观察、分析和归纳的能力
3、情感态度与价值观
① 通过经历直观动态的高尔顿试验,提高学习数学的兴趣
② 通过联系实际,让学生发现现实生活中有哪些例子服从或近似服从正态分布,是学生认识到数学知识来源于生活、服务于生活
③通过原则的学习,充分感受数学的对称美
教学重点、难点
重点:正态分布密度曲线的特点,利用原则解决一些简单的与正态分布有关的概率计算问题
难点:正态分布密度曲线的特点
教学过程:
创设情境
首先通过高尔顿板实验向学生演示了小球落下的规律。
具体操作如下:自上端放入一小球,任其自由下落,在下落过程中小球碰到下一排钉子,最后落入底板中的某个格。因此任意放入一个球,小球最后落入某个格子内事先是难以确定的,但是实验证明,如果放入大量球的话则其最后呈现的曲线总是雷同的,也就是说落入格中的小球的频率趋向稳定。
给学生演示操作,让学生更直观地看到小球动态的落入情况,提高了学生的学习兴趣。
随着实验重复次数的增加,频率直方图的形状会越来越像一条钟形曲线。
新课讲授
(1)正态曲线
观察上面曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:
式中的实数、是参数,分别表示总体的平均数与标准差,的图象为正态分布密度曲线,简称正态曲线.
(2)正态分布
一般地,如果对于任何实数,随机变量X满足
,
则称 X 的分布为正态(normaldistribution ) .
正态分布完全由参数和确定,因此正态分布常记作.如果随机变量 X 服从正态分布,则记为X~.
联系实际
在现实生活中,很多随机变量都服从或近似服从正态分布,那么大家能举出一些例子吗?
请大家开始讨论:
零件的尺寸、年降雨量、在正常条件下纤维的强度和张力;农作物的产量,小麦的穗长、株高;测量误差,射击目标的水平偏差等等,都服从或近似服从这样一种分布——正态分布.
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中,并且在概率和统计中占有重要地位。
正态曲线的特点
(1)曲线在x轴的上方,与x轴不相交
(2)曲线关于直线x=μ对称
(3)当x=μ时,曲线位于最高点
(4)曲线与x轴之间的面积为1
通过几何画板的演示:
学生又得出两个性质:
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
特殊区间的概率
若~,则对于任何实数,
为图中阴影部分的面积
对于固定的和a而言,该面积随着的减少而变化,这说明越小,X落在区间的概率越大,即X集中在周围概率越大。
特别有:
上述结果可用下图表示:
可以看到,正态总体几乎总取值于区间之内,而在此区间以外取值的概率只有0.0026,通常认为这种情况在一次试验中几乎不可能发生。在实际应用中就只考虑这个区间,称为原则.
例题分析
把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2;
D.以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
课堂小结
了解正态曲线、正态分布的概念,
知道正态曲线的解析式及曲线的特点。
3. 能够结合现实理解正态分布在现实生活中的应用。
教学反思
在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布
板书设计
正态分布
解析式曲线性质 ⑴ ⑵ ⑶ ⑷ ⑸3.3原则 例1. 例2①②③④ 例3 多媒体投影
