【课时作业】第12章 整式的乘除 复习课(含答案)2024-2025学年数学华东师大版八年级上册
文档属性
| 名称 | 【课时作业】第12章 整式的乘除 复习课(含答案)2024-2025学年数学华东师大版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 66.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 20:33:40 | ||
图片预览

文档简介
第12章 整式的乘除 复习课
一、作业目标
1.会同底数幂的乘法运算;
2.会单(多)项式与多项式相乘;
3.能选择合适的方法分解因式;
4.体会数式通性和从具体到抽象的思想在研究数学问题中的作用.
二、作业内容
1.对于①x-3xy=x(1-3y),② (x+3)(x-1)=x2+2x-3,从左到右的变形,表述正确的是 ( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
2.下列运算正确的是 ( )
A.(-a2)3=-a5
B.a3·a5=a15
C.(-a2b3)2=a4b6
D.3a2-2a2=1
3.下列因式分解正确的是 ( )
A.a(a-b)-b(a-b)= (a-b)(a+b)
B.a2-9b2=(a-3b)2
C.a2+4ab+4b2=(a+2b)2
D.a2-ab+a=a(a-b)
4.将9.52变形正确的是 ( )
A.9.52=92+0.52
B.9.52=(10+0.5)×(10-0.5)
C.9.52=102-2×10×0.5+0.52
D.9.52=92+9×0.5+0.52
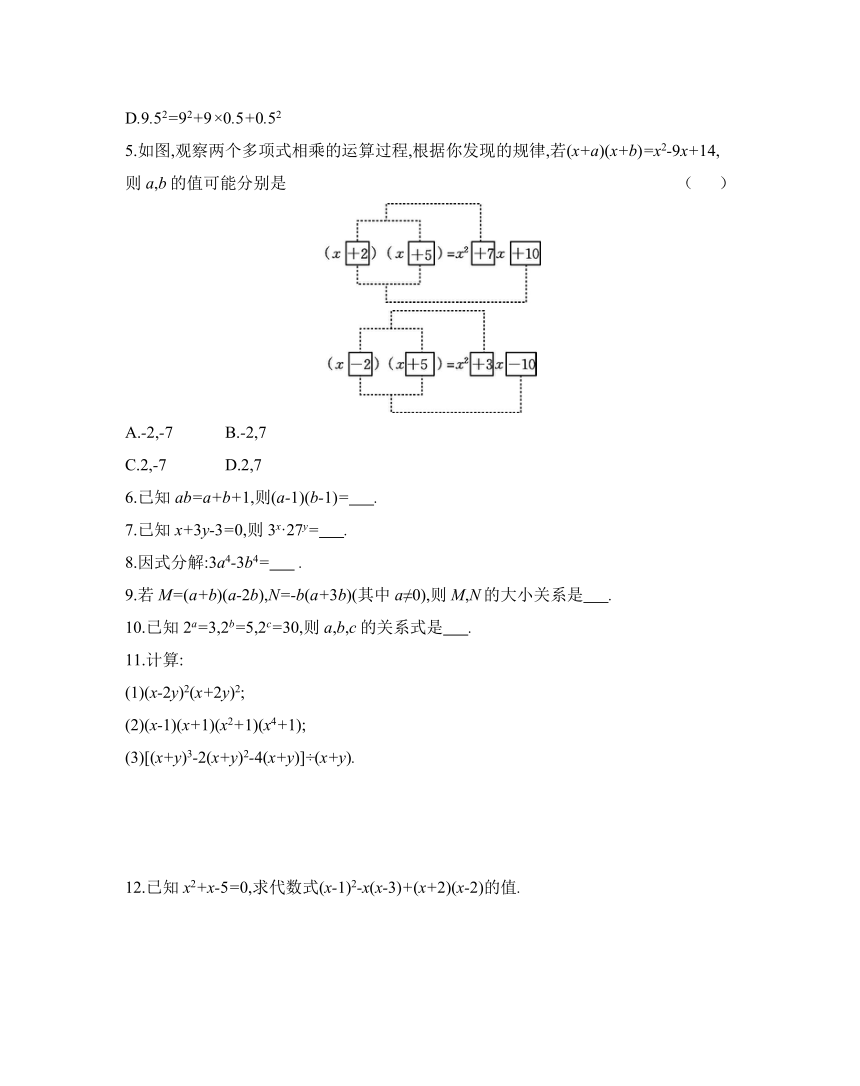
5.如图,观察两个多项式相乘的运算过程,根据你发现的规律,若(x+a)(x+b)=x2-9x+14,则a,b的值可能分别是 ( )
A.-2,-7 B.-2,7
C.2,-7 D.2,7
6.已知ab=a+b+1,则(a-1)(b-1)= .
7.已知x+3y-3=0,则3x·27y= .
8.因式分解:3a4-3b4= .
9.若M=(a+b)(a-2b),N=-b(a+3b)(其中a≠0),则M,N的大小关系是 .
10.已知2a=3,2b=5,2c=30,则a,b,c的关系式是 .
11.计算:
(1)(x-2y)2(x+2y)2;
(2)(x-1)(x+1)(x2+1)(x4+1);
(3)[(x+y)3-2(x+y)2-4(x+y)]÷(x+y).
12.已知x2+x-5=0,求代数式(x-1)2-x(x-3)+(x+2)(x-2)的值.
.
13.分解因式:(1)4x2-25y2;(2)4x2-12xy2+9y4.
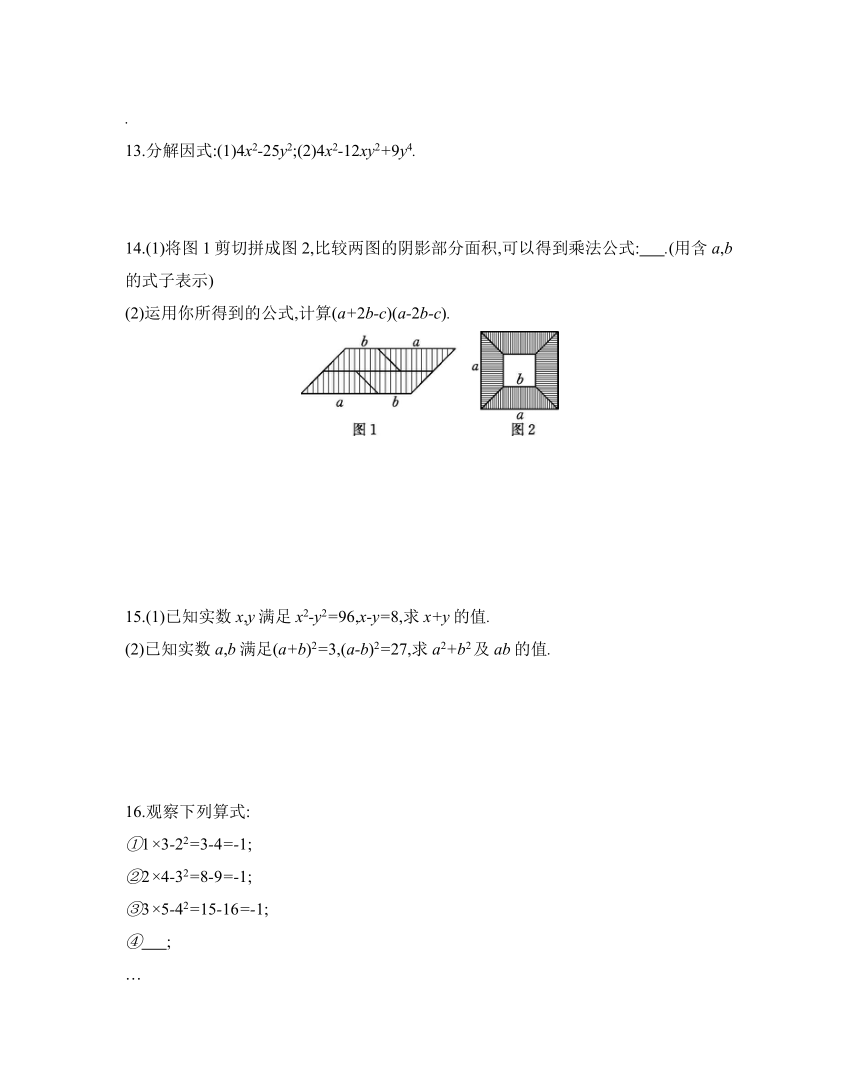
14.(1)将图1剪切拼成图2,比较两图的阴影部分面积,可以得到乘法公式: .(用含a,b的式子表示)
(2)运用你所得到的公式,计算(a+2b-c)(a-2b-c).
15.(1)已知实数x,y满足x2-y2=96,x-y=8,求x+y的值.
(2)已知实数a,b满足(a+b)2=3,(a-b)2=27,求a2+b2及ab的值.
16.观察下列算式:
①1×3-22=3-4=-1;
②2×4-32=8-9=-1;
③3×5-42=15-16=-1;
④ ;
…
(1)请你按以上规律写出第4个算式.
(2)把这个规律用含字母的式子表示出来.
(3)你认为(2)中所写出的式子一定成立吗 并说明理由.
参考答案
1.C 2.C 3.C 4.C 5.A
6.2 7.27 8.3(a2+b2)(a+b)(a-b)
9.M>N 10.c=1+a+b
11.解:(1)x4-8x2y2+16y4.
(2)x8-1.
(3)x2+y2+2xy-2x-2y-4.
12.解:原式=x2-2x+1-x2+3x+x2-4=x2+x-3.
∵x2+x-5=0,
∴x2+x=5,
∴原式=5-3=2.
13.解:(1)4x2-25y2=(2x)2-(5y)2=(2x+5y)(2x-5y).
(2)4x2-12xy2+9y4=(2x)2-12xy2+(3y2)2=(2x-3y2)2.
14.解:(1)(a+b)(a-b)=a2-b2.
(2)(a+2b-c)(a-2b-c)
=[(a-c)+2b][(a-c)-2b]
=(a-c)2-(2b)2
=a2-2ac+c2-4b2.
15.解:(1)∵x2-y2=96,
∴(x+y)(x-y)=96.
∵x-y=8,
∴x+y=12.
(2)∵(a+b)2=3,(a-b)2=27,
∴a2+2ab+b2=3,a2-2ab+b2=27,
∴2a2+2b2=30,4ab=-24,
∴a2+b2=15,ab=-6.
16.解:(1)4×6-52=24-25=-1.
(2)答案不唯一,如n(n+2)-(n+1)2=-1.
(3)成立.理由n(n+2)-(n+1)2=n2+2n-(n2+2n+1)
=n2+2n-n2-2n-1
=-1.
一、作业目标
1.会同底数幂的乘法运算;
2.会单(多)项式与多项式相乘;
3.能选择合适的方法分解因式;
4.体会数式通性和从具体到抽象的思想在研究数学问题中的作用.
二、作业内容
1.对于①x-3xy=x(1-3y),② (x+3)(x-1)=x2+2x-3,从左到右的变形,表述正确的是 ( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
2.下列运算正确的是 ( )
A.(-a2)3=-a5
B.a3·a5=a15
C.(-a2b3)2=a4b6
D.3a2-2a2=1
3.下列因式分解正确的是 ( )
A.a(a-b)-b(a-b)= (a-b)(a+b)
B.a2-9b2=(a-3b)2
C.a2+4ab+4b2=(a+2b)2
D.a2-ab+a=a(a-b)
4.将9.52变形正确的是 ( )
A.9.52=92+0.52
B.9.52=(10+0.5)×(10-0.5)
C.9.52=102-2×10×0.5+0.52
D.9.52=92+9×0.5+0.52
5.如图,观察两个多项式相乘的运算过程,根据你发现的规律,若(x+a)(x+b)=x2-9x+14,则a,b的值可能分别是 ( )
A.-2,-7 B.-2,7
C.2,-7 D.2,7
6.已知ab=a+b+1,则(a-1)(b-1)= .
7.已知x+3y-3=0,则3x·27y= .
8.因式分解:3a4-3b4= .
9.若M=(a+b)(a-2b),N=-b(a+3b)(其中a≠0),则M,N的大小关系是 .
10.已知2a=3,2b=5,2c=30,则a,b,c的关系式是 .
11.计算:
(1)(x-2y)2(x+2y)2;
(2)(x-1)(x+1)(x2+1)(x4+1);
(3)[(x+y)3-2(x+y)2-4(x+y)]÷(x+y).
12.已知x2+x-5=0,求代数式(x-1)2-x(x-3)+(x+2)(x-2)的值.
.
13.分解因式:(1)4x2-25y2;(2)4x2-12xy2+9y4.
14.(1)将图1剪切拼成图2,比较两图的阴影部分面积,可以得到乘法公式: .(用含a,b的式子表示)
(2)运用你所得到的公式,计算(a+2b-c)(a-2b-c).
15.(1)已知实数x,y满足x2-y2=96,x-y=8,求x+y的值.
(2)已知实数a,b满足(a+b)2=3,(a-b)2=27,求a2+b2及ab的值.
16.观察下列算式:
①1×3-22=3-4=-1;
②2×4-32=8-9=-1;
③3×5-42=15-16=-1;
④ ;
…
(1)请你按以上规律写出第4个算式.
(2)把这个规律用含字母的式子表示出来.
(3)你认为(2)中所写出的式子一定成立吗 并说明理由.
参考答案
1.C 2.C 3.C 4.C 5.A
6.2 7.27 8.3(a2+b2)(a+b)(a-b)
9.M>N 10.c=1+a+b
11.解:(1)x4-8x2y2+16y4.
(2)x8-1.
(3)x2+y2+2xy-2x-2y-4.
12.解:原式=x2-2x+1-x2+3x+x2-4=x2+x-3.
∵x2+x-5=0,
∴x2+x=5,
∴原式=5-3=2.
13.解:(1)4x2-25y2=(2x)2-(5y)2=(2x+5y)(2x-5y).
(2)4x2-12xy2+9y4=(2x)2-12xy2+(3y2)2=(2x-3y2)2.
14.解:(1)(a+b)(a-b)=a2-b2.
(2)(a+2b-c)(a-2b-c)
=[(a-c)+2b][(a-c)-2b]
=(a-c)2-(2b)2
=a2-2ac+c2-4b2.
15.解:(1)∵x2-y2=96,
∴(x+y)(x-y)=96.
∵x-y=8,
∴x+y=12.
(2)∵(a+b)2=3,(a-b)2=27,
∴a2+2ab+b2=3,a2-2ab+b2=27,
∴2a2+2b2=30,4ab=-24,
∴a2+b2=15,ab=-6.
16.解:(1)4×6-52=24-25=-1.
(2)答案不唯一,如n(n+2)-(n+1)2=-1.
(3)成立.理由n(n+2)-(n+1)2=n2+2n-(n2+2n+1)
=n2+2n-n2-2n-1
=-1.
