【课时作业】第13章 全等三角形 复习课(含答案)2024-2025学年数学华东师大版八年级上册
文档属性
| 名称 | 【课时作业】第13章 全等三角形 复习课(含答案)2024-2025学年数学华东师大版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 130.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 20:35:04 | ||
图片预览


文档简介
第13章 全等三角形 复习课
一、作业目标
能灵活应用各种判定方法识别全等三角形,并能通过全等三角形解决线段或角相等的问题.
二、作业内容
1.用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是 ( )
A.SAS B.ASA
C.AAS D.SSS
2.如图,请看以下两个推理过程:
①因为∠D=∠B, ∠E=∠C,DE=BC,所以△ADE≌△ABC(AAS);②因为∠DAE=∠BAC, ∠E=∠C,DE=BC,所以△ADE≌△ABC(AAS).则下列判断(包括判定三角形全等的依据)正确的是 ( )
A.①对,②错
B.①错,②对
C.①②都对
D.①②都错
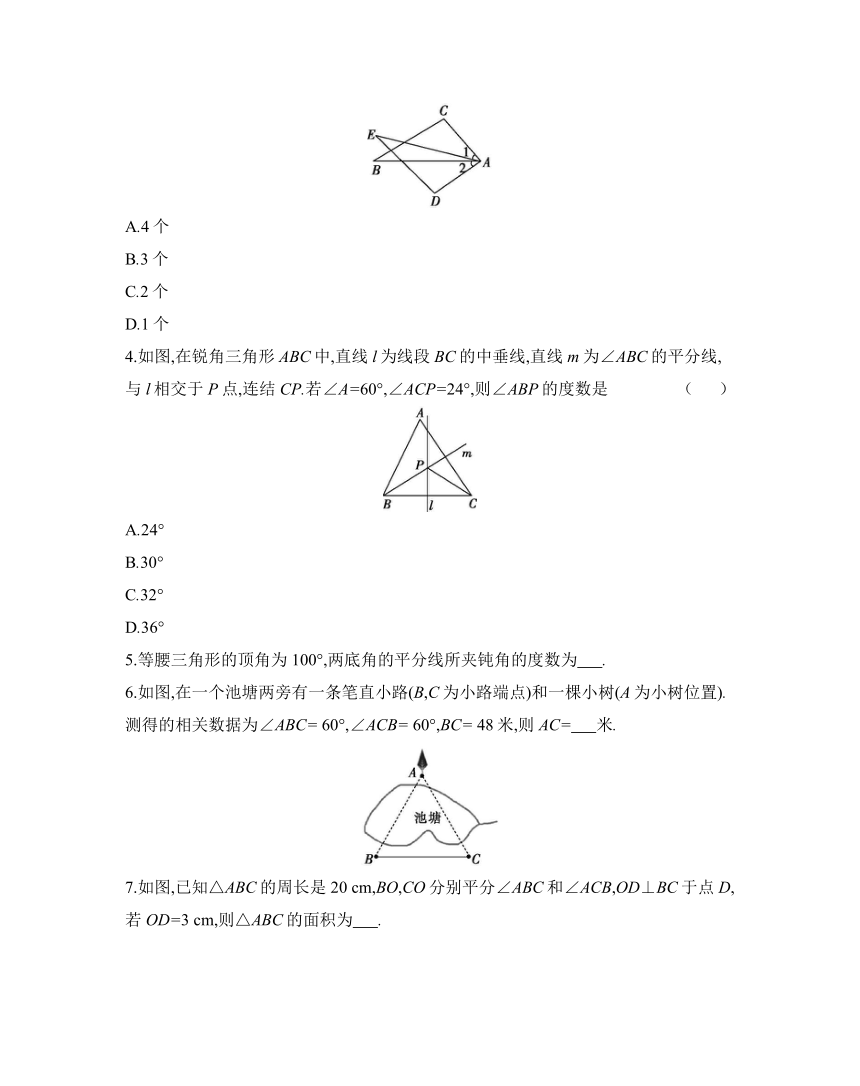
3.如图,已知∠1=∠2,AC=AD,增加下列条件:
①AB=AE;
②BC=ED;
③∠C=∠D;
④∠B=∠E.
其中能使△ABC≌△AED的条件有 ( )
A.4个
B.3个
C.2个
D.1个
4.如图,在锐角三角形ABC中,直线l为线段BC的中垂线,直线m为∠ABC的平分线,与l相交于P点,连结CP.若∠A=60°,∠ACP=24°,则∠ABP的度数是 ( )
A.24°
B.30°
C.32°
D.36°
5.等腰三角形的顶角为100°,两底角的平分线所夹钝角的度数为 .
6.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为∠ABC= 60°,∠ACB= 60°,BC= 48米,则AC= 米.
7.如图,已知△ABC的周长是20 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3 cm,则△ABC的面积为 .
8.在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=20 cm,则△DEB的周长为 .
9.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,用圆规和直尺作图,用两种方法把它分成两个三角形,且要求其中一个三角形是等腰三角形.(保留作图痕迹,不要求写作法和证明)
10.如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:AC=CD.
11.(主题情境题)如图1,这是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P,AP是∠BAC的平分线吗 请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
参考答案
1.D 2.B 3.B 4.C
5.140° 6.48 7.30 cm2 8.20 cm
9.解:第一种方法:利用30度的角所对的直角边是斜边的一半,可作AB边上的中线.
第二种方法:∠CAB=30°,∠B=60°∴作∠CBA的平分线.
第三种方法:在CA上取一点D,使CD=CB.
10.证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
∴△ABC≌△CED,
∴AC=CD.
11.解:(1)AP是∠BAC的平分线.
理由:在△ADF和△AEF中,
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)如图,过点P作PG⊥AC于点G.
∵AP平分∠BAC,PQ⊥AB,
∴PG=PQ=6.
∵S△ABC=S△ABP+S△APC=AB·PQ+AC·PG,
∴AB×6+×9×6=60,
∴AB=11.
一、作业目标
能灵活应用各种判定方法识别全等三角形,并能通过全等三角形解决线段或角相等的问题.
二、作业内容
1.用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是 ( )
A.SAS B.ASA
C.AAS D.SSS
2.如图,请看以下两个推理过程:
①因为∠D=∠B, ∠E=∠C,DE=BC,所以△ADE≌△ABC(AAS);②因为∠DAE=∠BAC, ∠E=∠C,DE=BC,所以△ADE≌△ABC(AAS).则下列判断(包括判定三角形全等的依据)正确的是 ( )
A.①对,②错
B.①错,②对
C.①②都对
D.①②都错
3.如图,已知∠1=∠2,AC=AD,增加下列条件:
①AB=AE;
②BC=ED;
③∠C=∠D;
④∠B=∠E.
其中能使△ABC≌△AED的条件有 ( )
A.4个
B.3个
C.2个
D.1个
4.如图,在锐角三角形ABC中,直线l为线段BC的中垂线,直线m为∠ABC的平分线,与l相交于P点,连结CP.若∠A=60°,∠ACP=24°,则∠ABP的度数是 ( )
A.24°
B.30°
C.32°
D.36°
5.等腰三角形的顶角为100°,两底角的平分线所夹钝角的度数为 .
6.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为∠ABC= 60°,∠ACB= 60°,BC= 48米,则AC= 米.
7.如图,已知△ABC的周长是20 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3 cm,则△ABC的面积为 .
8.在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=20 cm,则△DEB的周长为 .
9.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,用圆规和直尺作图,用两种方法把它分成两个三角形,且要求其中一个三角形是等腰三角形.(保留作图痕迹,不要求写作法和证明)
10.如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:AC=CD.
11.(主题情境题)如图1,这是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P,AP是∠BAC的平分线吗 请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
参考答案
1.D 2.B 3.B 4.C
5.140° 6.48 7.30 cm2 8.20 cm
9.解:第一种方法:利用30度的角所对的直角边是斜边的一半,可作AB边上的中线.
第二种方法:∠CAB=30°,∠B=60°∴作∠CBA的平分线.
第三种方法:在CA上取一点D,使CD=CB.
10.证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
∴△ABC≌△CED,
∴AC=CD.
11.解:(1)AP是∠BAC的平分线.
理由:在△ADF和△AEF中,
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)如图,过点P作PG⊥AC于点G.
∵AP平分∠BAC,PQ⊥AB,
∴PG=PQ=6.
∵S△ABC=S△ABP+S△APC=AB·PQ+AC·PG,
∴AB×6+×9×6=60,
∴AB=11.
