【课时作业】第14章 勾股定理 复习课(含答案)2024-2025学年数学华东师大版八年级上册
文档属性
| 名称 | 【课时作业】第14章 勾股定理 复习课(含答案)2024-2025学年数学华东师大版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 72.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览

文档简介
第14章 勾股定理 复习课
一、作业目标
1.会勾股定理的证明方法及运算.
2.会运用勾股定理的逆定理证明直角三角形.
3.利用勾股定理求最短路径.
4.勾股定理的实际应用.
二、作业内容
1.在△ABC中,下列说法错误的是 ( )
A.如果∠C-∠B=∠A,则△ABC为直角三角形
B.如果∠C=90°,则c2-a2=b2
C.如果(a+b)(a-b)=c2,则△ABC为直角三角形
D.如果∠C∶∠B∶∠A=12∶13∶15,则△ABC为直角三角形
2.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为 ( )
A. B. C. D.
3.在△ABC中,若AB=15,AC=13,高AD=12,则△ABC的周长是 ( )
A.42 B.32
C.42或32 D.37或33
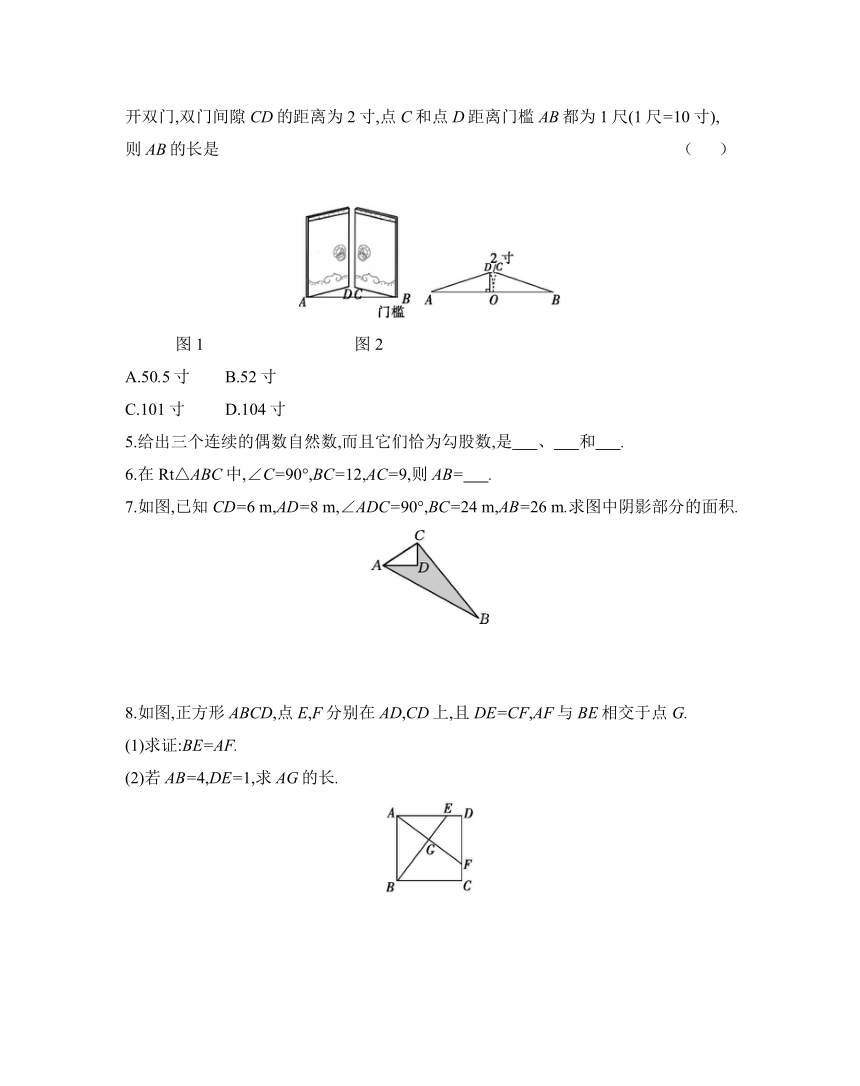
4.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意如下:如图1,图2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是 ( )
图1 图2
A.50.5寸 B.52寸
C.101寸 D.104寸
5.给出三个连续的偶数自然数,而且它们恰为勾股数,是 、 和 .
6.在Rt△ABC中,∠C=90°,BC=12,AC=9,则AB= .
7.如图,已知CD=6 m,AD=8 m,∠ADC=90°,BC=24 m,AB=26 m.求图中阴影部分的面积.
8.如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF.
(2)若AB=4,DE=1,求AG的长.
9.(主题情境题)如图1, 大正方形的面积可以表示为(a+b)2,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即a2+2ab+b2.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:
(a+b)2=a2+2ab+b2.
把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图2中图形的面积关系,直接写出一个多项式进行因式分解的等式.
(2) 如图3,Rt△ABC中,∠C=90°,CA=3,CB=4,CH是斜边AB边上的高.用上述“面积法”求CH的长.
(3)如图4,等腰△ABC中,AB=AC,点O为底边BC上任意点,OM⊥AB, ON⊥AC, CH⊥AB,垂足分别为M,N,H,连结AO,用上述“面积法”求证: OM+ON=CH.
图1 图2
图3 图4
参考答案
1.D 2.C 3.C 4.C
5.6 8 10
6.15
7.解:在Rt△ADC中,
∵CD=6 m,AD=8 m,BC=24 m,AB=26 m,
∴AC2=AD2+CD2=82+62=100,
∴AC=10 m.
在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°,
∴S阴影=AC×BC-AD×CD=×10×24-×8×6=96(m2),
即图中阴影部分的面积为96 m2.
8.解:(1)证明:∵四边形ABCD是正方形,∴∠BAE=∠ADF=90°,AB=AD=CD.
∵DE=CF,∴AE=DF.
在△BAE和△ADF中,,
∴△BAE≌△ADF(SAS),
∴BE=AF.
(2)由(1)得△BAE≌△ADF,
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°.
∵AB=4,DE=1,∴AE=3,∴BE===5.
在Rt△ABE中,AB·AE=BE·AG,∴AG==.
9.解:(1)x2+5x+6=(x+2)( x+3).
(2)Rt△ABC中,∠C=90°,CA=3,CB=4,AB===5.由三角形的面积法得CH===.
(3)等腰△ABC中, OM⊥AB,ON⊥AC,CH⊥AB,△ABC面积可表示为 AB·CH,也可表示为AB·OM+AC·ON,所以AB·CH=AB·OM+AC·ON.因为AB=AC,所以OM+ON=CH.
一、作业目标
1.会勾股定理的证明方法及运算.
2.会运用勾股定理的逆定理证明直角三角形.
3.利用勾股定理求最短路径.
4.勾股定理的实际应用.
二、作业内容
1.在△ABC中,下列说法错误的是 ( )
A.如果∠C-∠B=∠A,则△ABC为直角三角形
B.如果∠C=90°,则c2-a2=b2
C.如果(a+b)(a-b)=c2,则△ABC为直角三角形
D.如果∠C∶∠B∶∠A=12∶13∶15,则△ABC为直角三角形
2.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为 ( )
A. B. C. D.
3.在△ABC中,若AB=15,AC=13,高AD=12,则△ABC的周长是 ( )
A.42 B.32
C.42或32 D.37或33
4.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意如下:如图1,图2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是 ( )
图1 图2
A.50.5寸 B.52寸
C.101寸 D.104寸
5.给出三个连续的偶数自然数,而且它们恰为勾股数,是 、 和 .
6.在Rt△ABC中,∠C=90°,BC=12,AC=9,则AB= .
7.如图,已知CD=6 m,AD=8 m,∠ADC=90°,BC=24 m,AB=26 m.求图中阴影部分的面积.
8.如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF.
(2)若AB=4,DE=1,求AG的长.
9.(主题情境题)如图1, 大正方形的面积可以表示为(a+b)2,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即a2+2ab+b2.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:
(a+b)2=a2+2ab+b2.
把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图2中图形的面积关系,直接写出一个多项式进行因式分解的等式.
(2) 如图3,Rt△ABC中,∠C=90°,CA=3,CB=4,CH是斜边AB边上的高.用上述“面积法”求CH的长.
(3)如图4,等腰△ABC中,AB=AC,点O为底边BC上任意点,OM⊥AB, ON⊥AC, CH⊥AB,垂足分别为M,N,H,连结AO,用上述“面积法”求证: OM+ON=CH.
图1 图2
图3 图4
参考答案
1.D 2.C 3.C 4.C
5.6 8 10
6.15
7.解:在Rt△ADC中,
∵CD=6 m,AD=8 m,BC=24 m,AB=26 m,
∴AC2=AD2+CD2=82+62=100,
∴AC=10 m.
在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°,
∴S阴影=AC×BC-AD×CD=×10×24-×8×6=96(m2),
即图中阴影部分的面积为96 m2.
8.解:(1)证明:∵四边形ABCD是正方形,∴∠BAE=∠ADF=90°,AB=AD=CD.
∵DE=CF,∴AE=DF.
在△BAE和△ADF中,,
∴△BAE≌△ADF(SAS),
∴BE=AF.
(2)由(1)得△BAE≌△ADF,
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°.
∵AB=4,DE=1,∴AE=3,∴BE===5.
在Rt△ABE中,AB·AE=BE·AG,∴AG==.
9.解:(1)x2+5x+6=(x+2)( x+3).
(2)Rt△ABC中,∠C=90°,CA=3,CB=4,AB===5.由三角形的面积法得CH===.
(3)等腰△ABC中, OM⊥AB,ON⊥AC,CH⊥AB,△ABC面积可表示为 AB·CH,也可表示为AB·OM+AC·ON,所以AB·CH=AB·OM+AC·ON.因为AB=AC,所以OM+ON=CH.
