北京市大峪中学2024-2025初二年级第一学期数学期中试卷(图片版,无答案)
文档属性
| 名称 | 北京市大峪中学2024-2025初二年级第一学期数学期中试卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 715.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 22:57:01 | ||
图片预览


文档简介
大峪中学 2024—2025 第一学期初二年级
数学学科期中考试试卷
一、选择题:在每小题给出的四个选项中,只有一项是符合
题目要求的.(共 8 小题,每小题 2 分,共 16 分).
1..下列计算正确的是
3
A. a3 a 2a4 B. a3 a9 C. (ab)3 a3b D. a8 a2 a4
2.如图,△ABC中 AB边上的高线为
(A)AD (B)CE
(C)AF (D)BG
3.如图,盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木
条,使其不变形,这种做法的根据是( )
A.两点之间,线段最短
B.三角形的稳定性
C.长方形的四个角都是直角
D.四边形的稳定性
4. 将两个含 30°和 45°的直角三角板如图放置,则∠α的度数是( )
A.10° B.15° C.20° D.25°
5. 如图为了测量 B点到河对而的目标 A之间的距离,在 B点
同侧选择了一点 C,测得 ABC 65 , ACB 35 ,然后
在 M处立了标杆,使 MBC 65 , MCB 35 ,得到
△MBC≌△ABC,所以测得MB的长就是 A,B两点间的距
离,这里判定△MBC≌△ABC的理由是( )
A. SAS B. AAS C. ASA D. SSS
1
6. 图中的四边形均为长方形,用等式表示下图中图形面积的运算为( )
A. a b 2 a2 2ab b2 B. a b a b a2 b2
C. a a b a2 ab 2D. a b a2 ab b2
7. 已知4y2 my 9是完全平方式,则m的值为()
A.6 B. 12 C. 6 D. 12
8. 设 a,b是实数,定义一种新运算 a☆b a b 2,下面有四个推断:
① a☆b b☆a ② a b 2☆ a2☆b2
③ a ☆b a☆ b ④ a☆ b c a☆b a☆c
其中所有正确推断的序号是
A.①②③④ B.①③④ C.①② D.①③
二、填空题:(共 8 小题,每小题 2 分,共 16 分).
9.三角形两边长分别是 4,6,则第三边边长 a的取值范围是 .
10.一个多边形的每个外角都是 40°,则这个多边形的边数是__________.
若a m 3,a n 2,则a 2m 3n11 . __________.
12.如图,△ABC中,∠B=20°,D是 BC延长线上一点,且∠ACD=60°,则∠A
的度数是____________.
第 12题图 第 13题图
13. 如图,△ABC中,∠A=90°, BD平分∠ABC,交 AC于点 D,DE⊥BC于 E,
若 AB=6, BC=10, AC=8, 则ΔCDE的周长为__________.
2
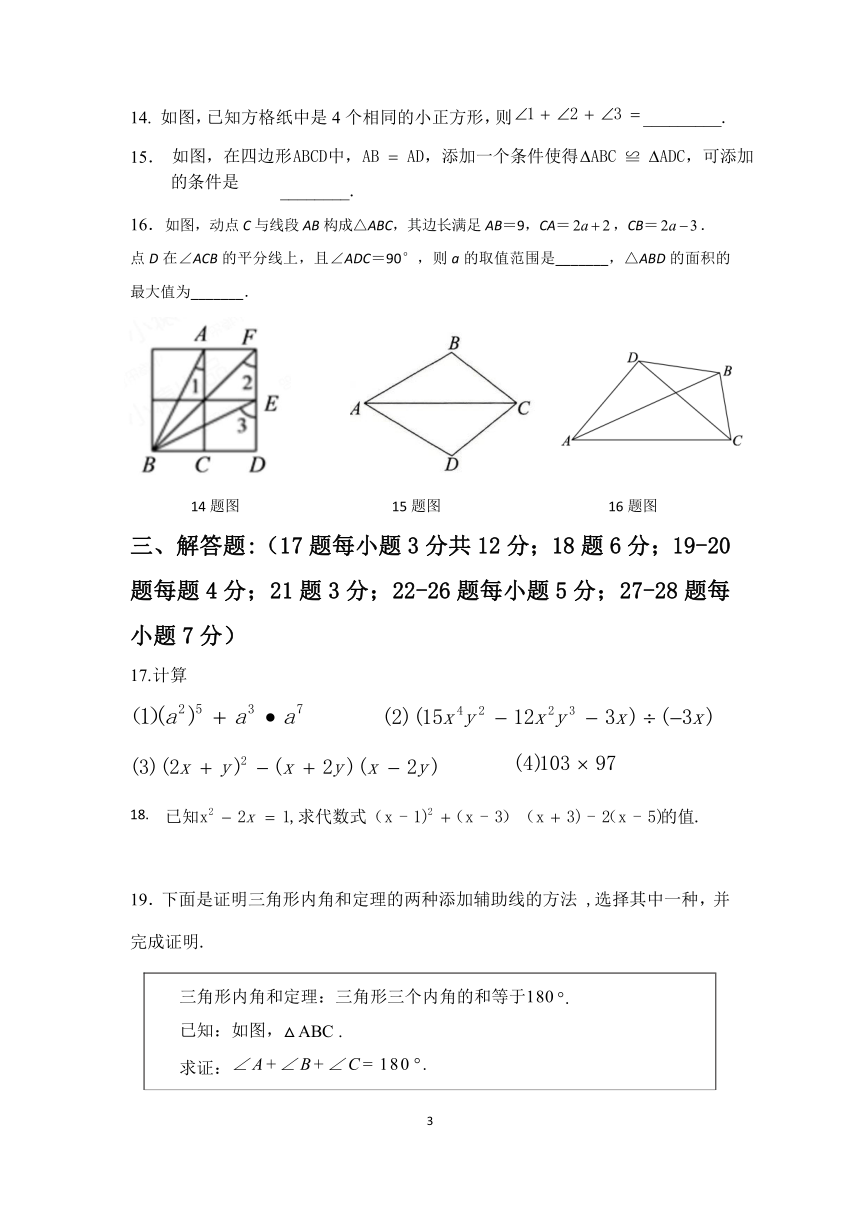
14. 如图,已知方格纸中是 4个相同的小正方形,则 1 2 3 _________.
15. 如图,在四边形ABCD中,AB AD,添加一个条件使得 ABC ≌ ADC,可添加
的条件是 ________.
16.如图,动点 C 与线段 AB构成△ABC,其边长满足 AB=9,CA=2a 2,CB=2a 3.
点 D 在∠ACB 的平分线上,且∠ADC=90°,则 a 的取值范围是_______,△ABD 的面积的
最大值为_______.
14 题图 15 题图 16 题图
三、解答题:(17 题每小题 3 分共 12 分;18 题 6 分;19-20
题每题 4 分;21 题 3 分;22-26 题每小题 5 分;27-28 题每
小题 7 分)
17.计算
(1)(a 2)5 a3 a7 (2)(15x 4y 2 12x 2y 3 3x) ( 3x)
(3)(2x y )2 (x 2y )(x 2y ) (4)103 97
18. 已知x2 2x 1,求代数式(x - 1)2 (x - 3)(x 3) - (2 x - 5)的值.
19.下面是证明三角形内角和定理的两种添加辅助线的方法 ,选择其中一种,并
完成证明.
三角形内角和定理:三角形三个内角的和等于180 °.
已知:如图,△ABC .
求证:∠ A+∠ B+∠ C= 180 ° .
3
方法一 方法二
证明:如图,过点A作 DE∥ BC. 证明:如图,过点C作CD∥ AB.
20. 如图,点 B,F,C,E在一条直线上,BF=CE,
AB∥ED,AC∥FD.求证:△ABC≌△DEF.
21. 已知:如图, ABC.
求作:点P,使得点P在 ABC内,且到三边AB,BC,CA的距离相等.
22.如图,在 ABC中,AD,AE分别是 ABC的高和角平分线.
若 B 30 , C 50 ,求 DAE的度数.
23.已知一个等腰三角形的两边长分别为 3cm和 8cm,求它的周长.
4
24.
(2) 从上面的计算中你发现的规律(用含 n的一般形式表示) .
25. 证明:当n是整数时,两个连续奇数的平方差(2n 1)2 (2n - 1)2是8的倍数.
26. 已知:如图,A、B、D三点在同一直线上,AC=BC ,DC=EC, ∠ACB =
∠DCE =90°,判断线段 AD与线段 BE的关系,并证明你的结论。
27.如图,在△ABC 中,∠ACB=90°,AC =BC,D 为射线 BC 上一点(不与点 B,C 重合),连
接 AD并延长到点 E,使得 DE=AD,连接 BE.过点 B 作 BE 的垂线交直线 AC 于点 F.
(1)如图 1,点 D 在线段 CB 上,且 DB①请补全图形;
②判断 CD,DB,CF 之间的数量关系,并证明.
(2)如图 2,若点 D在线段 BC 的延长线上,请画出图形,直接写出 CD,DB,
CF 之间的数量关系.
图 1 图 2
5
28.在平面直角坐标系 xOy中,对于点 P 和点 A,若存在点 Q,使得 PAQ 90 ,且
AQ AP,则称点 Q 为点 P 关于点 A 的“链垂点”.
(1)如图 1,
①若点 A 的坐标为 2,1 ,则点 A 关于点 O 的“链垂点”坐标为__________;
②若点 B(5,3)为点 O 关于点 C 的“链垂点”,且点 C 位于 x 轴上方,试求点 C 的坐标;
(2)如图 2,图形 G 是端点为 1,0 和 2,1 的线段,图形 H 是以点 O 为中心,各边分别与
坐标轴平行且边长为 6 的正方形,点 D为图形 G 上的动点,对于点E 0,t (t<0),存在
点 D,使得点 D关于点 E 的“链垂点”恰好在图形 H 上,请直接写出 t 的取值范围.
图 1 图 2
6
数学学科期中考试试卷
一、选择题:在每小题给出的四个选项中,只有一项是符合
题目要求的.(共 8 小题,每小题 2 分,共 16 分).
1..下列计算正确的是
3
A. a3 a 2a4 B. a3 a9 C. (ab)3 a3b D. a8 a2 a4
2.如图,△ABC中 AB边上的高线为
(A)AD (B)CE
(C)AF (D)BG
3.如图,盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉一根木
条,使其不变形,这种做法的根据是( )
A.两点之间,线段最短
B.三角形的稳定性
C.长方形的四个角都是直角
D.四边形的稳定性
4. 将两个含 30°和 45°的直角三角板如图放置,则∠α的度数是( )
A.10° B.15° C.20° D.25°
5. 如图为了测量 B点到河对而的目标 A之间的距离,在 B点
同侧选择了一点 C,测得 ABC 65 , ACB 35 ,然后
在 M处立了标杆,使 MBC 65 , MCB 35 ,得到
△MBC≌△ABC,所以测得MB的长就是 A,B两点间的距
离,这里判定△MBC≌△ABC的理由是( )
A. SAS B. AAS C. ASA D. SSS
1
6. 图中的四边形均为长方形,用等式表示下图中图形面积的运算为( )
A. a b 2 a2 2ab b2 B. a b a b a2 b2
C. a a b a2 ab 2D. a b a2 ab b2
7. 已知4y2 my 9是完全平方式,则m的值为()
A.6 B. 12 C. 6 D. 12
8. 设 a,b是实数,定义一种新运算 a☆b a b 2,下面有四个推断:
① a☆b b☆a ② a b 2☆ a2☆b2
③ a ☆b a☆ b ④ a☆ b c a☆b a☆c
其中所有正确推断的序号是
A.①②③④ B.①③④ C.①② D.①③
二、填空题:(共 8 小题,每小题 2 分,共 16 分).
9.三角形两边长分别是 4,6,则第三边边长 a的取值范围是 .
10.一个多边形的每个外角都是 40°,则这个多边形的边数是__________.
若a m 3,a n 2,则a 2m 3n11 . __________.
12.如图,△ABC中,∠B=20°,D是 BC延长线上一点,且∠ACD=60°,则∠A
的度数是____________.
第 12题图 第 13题图
13. 如图,△ABC中,∠A=90°, BD平分∠ABC,交 AC于点 D,DE⊥BC于 E,
若 AB=6, BC=10, AC=8, 则ΔCDE的周长为__________.
2
14. 如图,已知方格纸中是 4个相同的小正方形,则 1 2 3 _________.
15. 如图,在四边形ABCD中,AB AD,添加一个条件使得 ABC ≌ ADC,可添加
的条件是 ________.
16.如图,动点 C 与线段 AB构成△ABC,其边长满足 AB=9,CA=2a 2,CB=2a 3.
点 D 在∠ACB 的平分线上,且∠ADC=90°,则 a 的取值范围是_______,△ABD 的面积的
最大值为_______.
14 题图 15 题图 16 题图
三、解答题:(17 题每小题 3 分共 12 分;18 题 6 分;19-20
题每题 4 分;21 题 3 分;22-26 题每小题 5 分;27-28 题每
小题 7 分)
17.计算
(1)(a 2)5 a3 a7 (2)(15x 4y 2 12x 2y 3 3x) ( 3x)
(3)(2x y )2 (x 2y )(x 2y ) (4)103 97
18. 已知x2 2x 1,求代数式(x - 1)2 (x - 3)(x 3) - (2 x - 5)的值.
19.下面是证明三角形内角和定理的两种添加辅助线的方法 ,选择其中一种,并
完成证明.
三角形内角和定理:三角形三个内角的和等于180 °.
已知:如图,△ABC .
求证:∠ A+∠ B+∠ C= 180 ° .
3
方法一 方法二
证明:如图,过点A作 DE∥ BC. 证明:如图,过点C作CD∥ AB.
20. 如图,点 B,F,C,E在一条直线上,BF=CE,
AB∥ED,AC∥FD.求证:△ABC≌△DEF.
21. 已知:如图, ABC.
求作:点P,使得点P在 ABC内,且到三边AB,BC,CA的距离相等.
22.如图,在 ABC中,AD,AE分别是 ABC的高和角平分线.
若 B 30 , C 50 ,求 DAE的度数.
23.已知一个等腰三角形的两边长分别为 3cm和 8cm,求它的周长.
4
24.
(2) 从上面的计算中你发现的规律(用含 n的一般形式表示) .
25. 证明:当n是整数时,两个连续奇数的平方差(2n 1)2 (2n - 1)2是8的倍数.
26. 已知:如图,A、B、D三点在同一直线上,AC=BC ,DC=EC, ∠ACB =
∠DCE =90°,判断线段 AD与线段 BE的关系,并证明你的结论。
27.如图,在△ABC 中,∠ACB=90°,AC =BC,D 为射线 BC 上一点(不与点 B,C 重合),连
接 AD并延长到点 E,使得 DE=AD,连接 BE.过点 B 作 BE 的垂线交直线 AC 于点 F.
(1)如图 1,点 D 在线段 CB 上,且 DB
②判断 CD,DB,CF 之间的数量关系,并证明.
(2)如图 2,若点 D在线段 BC 的延长线上,请画出图形,直接写出 CD,DB,
CF 之间的数量关系.
图 1 图 2
5
28.在平面直角坐标系 xOy中,对于点 P 和点 A,若存在点 Q,使得 PAQ 90 ,且
AQ AP,则称点 Q 为点 P 关于点 A 的“链垂点”.
(1)如图 1,
①若点 A 的坐标为 2,1 ,则点 A 关于点 O 的“链垂点”坐标为__________;
②若点 B(5,3)为点 O 关于点 C 的“链垂点”,且点 C 位于 x 轴上方,试求点 C 的坐标;
(2)如图 2,图形 G 是端点为 1,0 和 2,1 的线段,图形 H 是以点 O 为中心,各边分别与
坐标轴平行且边长为 6 的正方形,点 D为图形 G 上的动点,对于点E 0,t (t<0),存在
点 D,使得点 D关于点 E 的“链垂点”恰好在图形 H 上,请直接写出 t 的取值范围.
图 1 图 2
6
同课章节目录
