【课时作业】14.1 全等三角形(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】14.1 全等三角形(含答案)2024-2025学年数学沪科版八年级上册 | 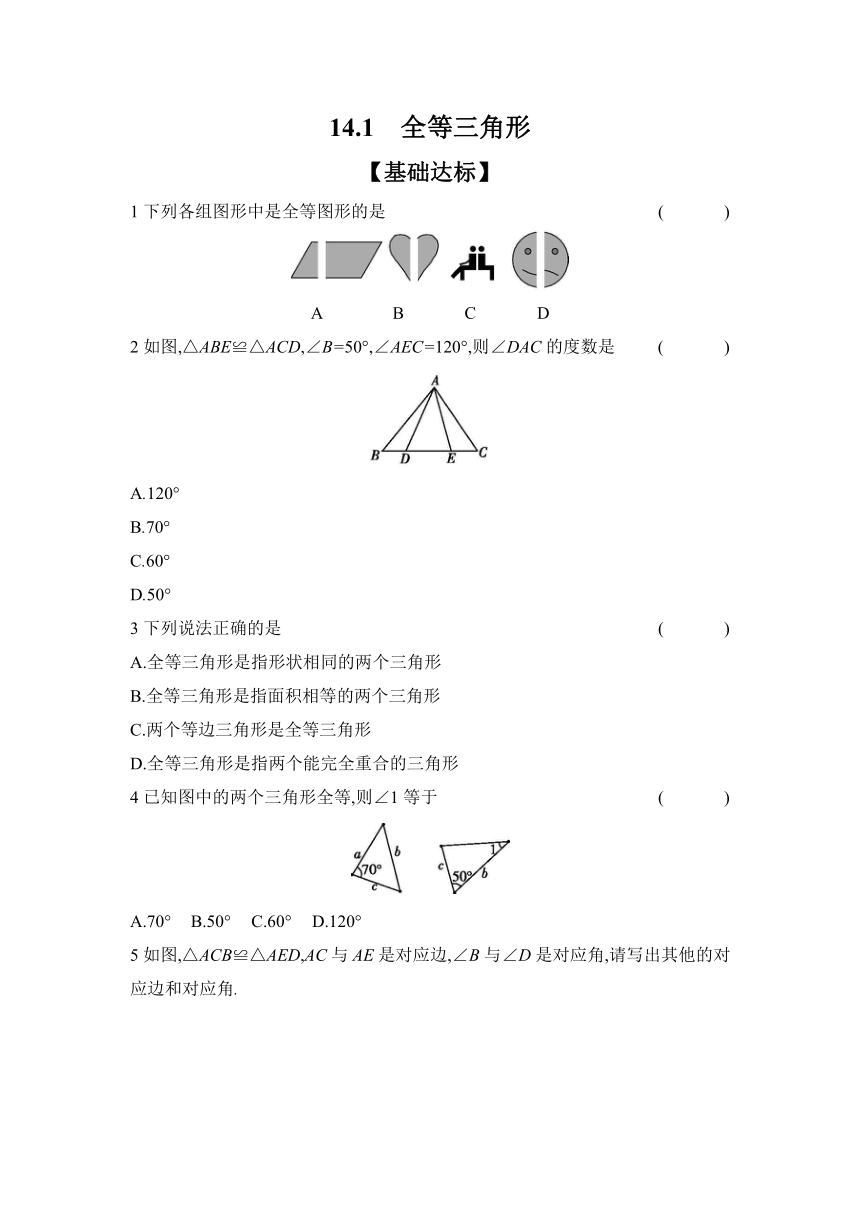 | |
| 格式 | docx | ||
| 文件大小 | 88.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 20:51:01 | ||
图片预览


文档简介
14.1 全等三角形
【基础达标】
1下列各组图形中是全等图形的是 ( )
A B C D
2如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是 ( )
A.120°
B.70°
C.60°
D.50°
3下列说法正确的是 ( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形
D.全等三角形是指两个能完全重合的三角形
4已知图中的两个三角形全等,则∠1等于 ( )
A.70° B.50° C.60° D.120°
5如图,△ACB≌△AED,AC与AE是对应边,∠B与∠D是对应角,请写出其他的对应边和对应角.
【能力巩固】
6如图,△ABC≌△ADE,BC与AD相交于点G,BC与DE相交于点F,∠D=45°,∠EAC=30°,则∠AGC的度数为 ( )
A.75° B.70° C.65° D.60°
7如图,△ABC≌△DBE,点D在线段AC上,线段BC与DE交于点F.下面各项中,不能推导出的结论是 ( )
A.∠EBF=∠ABD
B.∠EBF=∠FDC
C.∠ABD=∠FDC
D.∠ABD=∠FBD
8如图,将△ABC绕点A旋转180°,得△ABC≌ ,对应边分别为 ,对应角分别为 .
9如图,△ABC≌△DEF,BE=4,AE=1,则DE= .
10如图,△ADF≌△BCE,∠B=32°,∠F=28°,BC=5 cm,CD=1 cm.求:
(1)∠1的度数;
(2)AC的长.
11如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,∠ACB=105°,∠CAD=25°,∠B=30°,则∠1的度数为多少
【素养拓展】
12如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明BD=DE+CE;
(2)当∠BAC满足什么条件时,BD∥CE
参考答案
1.B 2.B 3.D 4.C
5.解:其他对应边:BC与DE,AB与AD.
其他对应角:∠C与∠E,∠CAB与∠EAD.
6.A 7.D
8.△AED AB和AE、BC和ED、AC和AD ∠1和∠2、∠B和∠E、∠C和∠D
9.5
10.解:(1)∵△ADF≌△BCE,∠F=28°,
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°.
(2)∵△ADF≌△BCE,BC=5 cm,
∴AD=BC=5 cm.
又∵CD=1 cm,∴AC=AD+CD=6 cm.
11.解:∵△ABC≌△ADE,
∴∠D=∠B=30°.
∵∠ACB=∠CAD+∠AFC,
∴∠AFC=105°-25°=80°,
∴∠1=180°-∠D-∠DFG=180°-80°-30°=70°.
12.解:(1)证明:∵△BAD≌△ACE,∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE.
(2)∠BAC=90°.
理由:
∵∠BAC=90°,∴∠BAE+∠CAE=90°.
∵△BAD≌△ACE,∴∠ABD=∠CAE,
∴∠ABD+∠BAD=90°,
∴∠ADB=90°,∠BDE=90°,∠AEC=∠ADB=90°,
∴∠BDE=∠AEC,∴BD∥CE.
【基础达标】
1下列各组图形中是全等图形的是 ( )
A B C D
2如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是 ( )
A.120°
B.70°
C.60°
D.50°
3下列说法正确的是 ( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形
D.全等三角形是指两个能完全重合的三角形
4已知图中的两个三角形全等,则∠1等于 ( )
A.70° B.50° C.60° D.120°
5如图,△ACB≌△AED,AC与AE是对应边,∠B与∠D是对应角,请写出其他的对应边和对应角.
【能力巩固】
6如图,△ABC≌△ADE,BC与AD相交于点G,BC与DE相交于点F,∠D=45°,∠EAC=30°,则∠AGC的度数为 ( )
A.75° B.70° C.65° D.60°
7如图,△ABC≌△DBE,点D在线段AC上,线段BC与DE交于点F.下面各项中,不能推导出的结论是 ( )
A.∠EBF=∠ABD
B.∠EBF=∠FDC
C.∠ABD=∠FDC
D.∠ABD=∠FBD
8如图,将△ABC绕点A旋转180°,得△ABC≌ ,对应边分别为 ,对应角分别为 .
9如图,△ABC≌△DEF,BE=4,AE=1,则DE= .
10如图,△ADF≌△BCE,∠B=32°,∠F=28°,BC=5 cm,CD=1 cm.求:
(1)∠1的度数;
(2)AC的长.
11如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,∠ACB=105°,∠CAD=25°,∠B=30°,则∠1的度数为多少
【素养拓展】
12如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明BD=DE+CE;
(2)当∠BAC满足什么条件时,BD∥CE
参考答案
1.B 2.B 3.D 4.C
5.解:其他对应边:BC与DE,AB与AD.
其他对应角:∠C与∠E,∠CAB与∠EAD.
6.A 7.D
8.△AED AB和AE、BC和ED、AC和AD ∠1和∠2、∠B和∠E、∠C和∠D
9.5
10.解:(1)∵△ADF≌△BCE,∠F=28°,
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°.
(2)∵△ADF≌△BCE,BC=5 cm,
∴AD=BC=5 cm.
又∵CD=1 cm,∴AC=AD+CD=6 cm.
11.解:∵△ABC≌△ADE,
∴∠D=∠B=30°.
∵∠ACB=∠CAD+∠AFC,
∴∠AFC=105°-25°=80°,
∴∠1=180°-∠D-∠DFG=180°-80°-30°=70°.
12.解:(1)证明:∵△BAD≌△ACE,∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE.
(2)∠BAC=90°.
理由:
∵∠BAC=90°,∴∠BAE+∠CAE=90°.
∵△BAD≌△ACE,∴∠ABD=∠CAE,
∴∠ABD+∠BAD=90°,
∴∠ADB=90°,∠BDE=90°,∠AEC=∠ADB=90°,
∴∠BDE=∠AEC,∴BD∥CE.
