【课时作业】第11章 平面直角坐标系(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第11章 平面直角坐标系(含答案)2024-2025学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 86.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 20:57:49 | ||
图片预览

文档简介
第11章 平面直角坐标系 复习课作业设计
一、作业目标
1.能够认识平面直角坐标系,了解点与坐标的对应关系.
2.掌握平面直角坐标系中点的平移与点的坐标关系的变化.
3.掌握平面直角坐标系中图形的平移规律.
二、作业内容
【基础达标】
1以下能够准确确定某一地方地理位置的是 ( )
A.离芜湖市200千米
B.安徽省内
C.在合肥市北方
D.东经117.77°,北纬31.51°
2如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-1),“马”位于点(2,-1),则“兵”位于点 ( )
A.(-1,2) B.(-3,2)
C.(-3,1) D.(-2,3)
3在平面直角坐标系中,若点A(a,b)在第二象限,则点B(-a,b)所在的象限是第 象限.
4在平面直角坐标系中,若点A(2,m+2)在x轴上,则m的值为 .
【能力巩固】
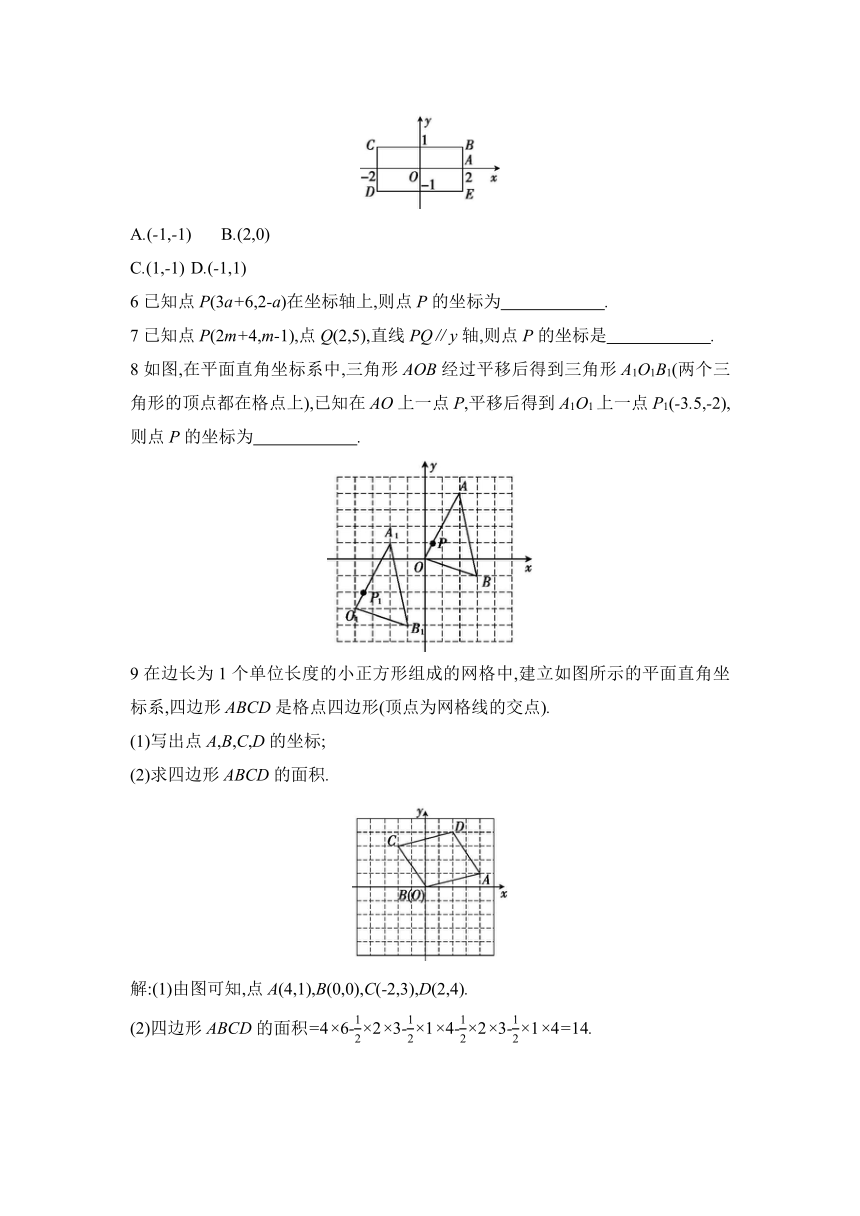
5如图,长方形BCDE的各边分别平行于x轴、y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边做环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动,则两个物体运动后的第2021次相遇地点的坐标是 ( )
A.(-1,-1) B.(2,0)
C.(1,-1) D.(-1,1)
6已知点P(3a+6,2-a)在坐标轴上,则点P的坐标为 .
7已知点P(2m+4,m-1),点Q(2,5),直线PQ∥y轴,则点P的坐标是 .
8如图,在平面直角坐标系中,三角形AOB经过平移后得到三角形A1O1B1(两个三角形的顶点都在格点上),已知在AO上一点P,平移后得到A1O1上一点P1(-3.5,-2),则点P的坐标为 .
9在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
解:(1)由图可知,点A(4,1),B(0,0),C(-2,3),D(2,4).
(2)四边形ABCD的面积=4×6-×2×3-×1×4-×2×3-×1×4=14.
【素养拓展】
10已知当m,n都是实数,且满足2m=8+n时,称pm-1,为“开心点”.
(1)判断点A(5,3)是否为“开心点”,并说明理由;
(2)若点M(a,2a-1)是“开心点”,则点M在第几象限 并说明理由.
参考答案
1.D 2.B
3.一
4.-2
5.A
6.(12,0)或(0,4)
7.(2,-2)
8.(0.5,1)
9.解:(1)由图可知,点A(4,1),B(0,0),C(-2,3),D(2,4).
(2)四边形ABCD的面积=4×6-×2×3-×1×4-×2×3-×1×4=14.
10.解:(1)点A(5,3)是“开心点”,理由如下:
因为A(5,3),所以m-1=5,=3,得m=6,n=4,
则2m=12,8+n=12,所以2m=8+n,所以A(5,3)是“开心点”.
(2)点M在第三象限,理由如下:
因为点M(a,2a-1)是“开心点”,
所以m-1=a,=2a-1,
所以m=a+1,n=4a-4,
代入2m=8+n有2a+2=8+4a-4,
所以a=-1,所以2a-1=-3,所以M(-1,-3),
故点M在第三象限.
一、作业目标
1.能够认识平面直角坐标系,了解点与坐标的对应关系.
2.掌握平面直角坐标系中点的平移与点的坐标关系的变化.
3.掌握平面直角坐标系中图形的平移规律.
二、作业内容
【基础达标】
1以下能够准确确定某一地方地理位置的是 ( )
A.离芜湖市200千米
B.安徽省内
C.在合肥市北方
D.东经117.77°,北纬31.51°
2如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-1),“马”位于点(2,-1),则“兵”位于点 ( )
A.(-1,2) B.(-3,2)
C.(-3,1) D.(-2,3)
3在平面直角坐标系中,若点A(a,b)在第二象限,则点B(-a,b)所在的象限是第 象限.
4在平面直角坐标系中,若点A(2,m+2)在x轴上,则m的值为 .
【能力巩固】
5如图,长方形BCDE的各边分别平行于x轴、y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边做环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动,则两个物体运动后的第2021次相遇地点的坐标是 ( )
A.(-1,-1) B.(2,0)
C.(1,-1) D.(-1,1)
6已知点P(3a+6,2-a)在坐标轴上,则点P的坐标为 .
7已知点P(2m+4,m-1),点Q(2,5),直线PQ∥y轴,则点P的坐标是 .
8如图,在平面直角坐标系中,三角形AOB经过平移后得到三角形A1O1B1(两个三角形的顶点都在格点上),已知在AO上一点P,平移后得到A1O1上一点P1(-3.5,-2),则点P的坐标为 .
9在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
解:(1)由图可知,点A(4,1),B(0,0),C(-2,3),D(2,4).
(2)四边形ABCD的面积=4×6-×2×3-×1×4-×2×3-×1×4=14.
【素养拓展】
10已知当m,n都是实数,且满足2m=8+n时,称pm-1,为“开心点”.
(1)判断点A(5,3)是否为“开心点”,并说明理由;
(2)若点M(a,2a-1)是“开心点”,则点M在第几象限 并说明理由.
参考答案
1.D 2.B
3.一
4.-2
5.A
6.(12,0)或(0,4)
7.(2,-2)
8.(0.5,1)
9.解:(1)由图可知,点A(4,1),B(0,0),C(-2,3),D(2,4).
(2)四边形ABCD的面积=4×6-×2×3-×1×4-×2×3-×1×4=14.
10.解:(1)点A(5,3)是“开心点”,理由如下:
因为A(5,3),所以m-1=5,=3,得m=6,n=4,
则2m=12,8+n=12,所以2m=8+n,所以A(5,3)是“开心点”.
(2)点M在第三象限,理由如下:
因为点M(a,2a-1)是“开心点”,
所以m-1=a,=2a-1,
所以m=a+1,n=4a-4,
代入2m=8+n有2a+2=8+4a-4,
所以a=-1,所以2a-1=-3,所以M(-1,-3),
故点M在第三象限.
