【课时作业】第11章 平面直角坐标系 测试卷(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第11章 平面直角坐标系 测试卷(含答案)2024-2025学年数学沪科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 21:28:34 | ||
图片预览


文档简介
第11章 平面直角坐标系 测试卷
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.已知点A(0,a)到x轴的距离是3,则a为 ( )
A.3 B.-3 C.±3 D.±6
2.若P(m,n)是第三象限内的点,则点Q(-n,0)在 ( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
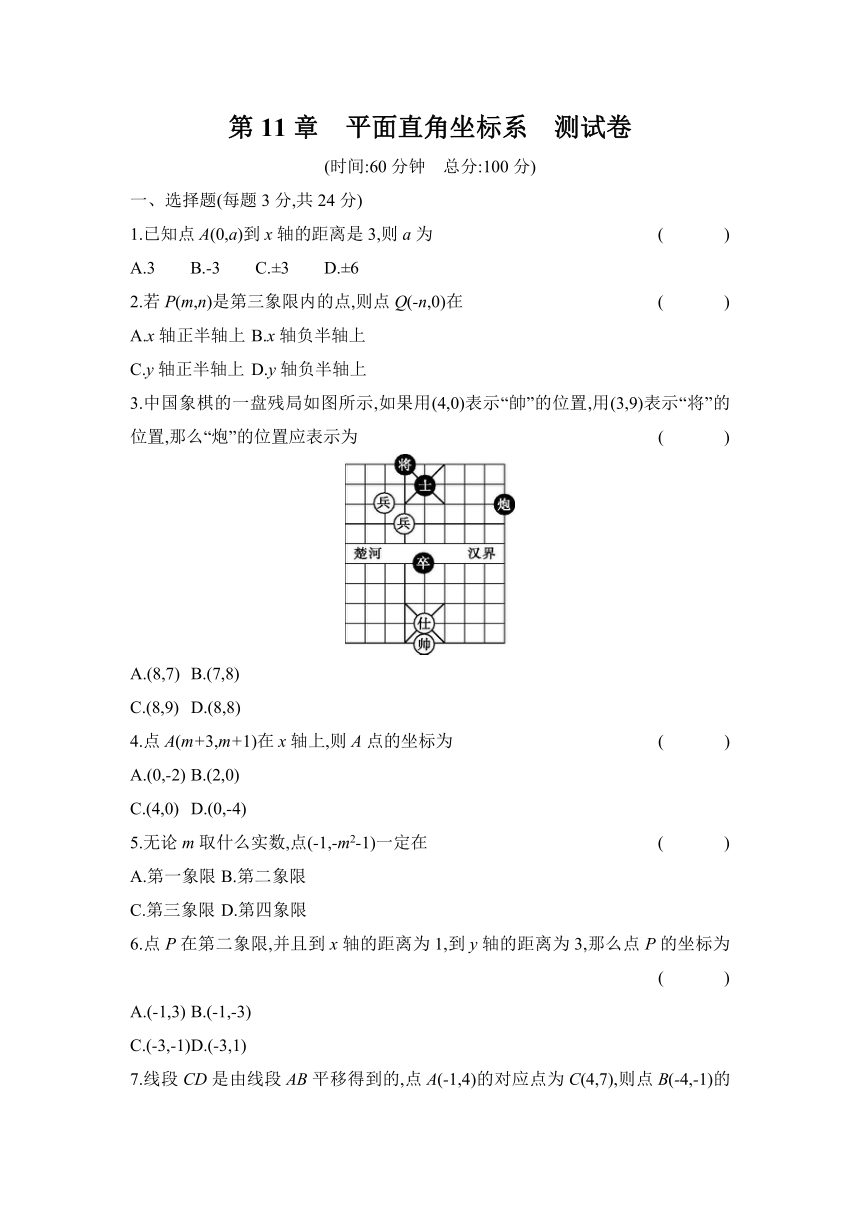
3.中国象棋的一盘残局如图所示,如果用(4,0)表示“帥”的位置,用(3,9)表示“将”的位置,那么“炮”的位置应表示为 ( )
A.(8,7) B.(7,8)
C.(8,9) D.(8,8)
4.点A(m+3,m+1)在x轴上,则A点的坐标为 ( )
A.(0,-2) B.(2,0)
C.(4,0) D.(0,-4)
5.无论m取什么实数,点(-1,-m2-1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.点P在第二象限,并且到x轴的距离为1,到y轴的距离为3,那么点P的坐标为 ( )
A.(-1,3) B.(-1,-3)
C.(-3,-1) D.(-3,1)
7.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 ( )
A.(2,9) B.(5,3)
C.(1,2) D.(-9,-4)
8.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…,表示,则顶点A55的坐标是 ( )
A.(13,13) B.(-13,-13)
C.(14,14) D.(-14,-14)
二、填空题(每题3分,共18分)
9.已知点P(3,-4),它到x轴的距离是 .
10.设点P(x,y)在第四象限,且x2=4,|y|=3,则点P的坐标为 .
11.若点A(x,4-2x)在第二、四象限夹角的平分线上,则x= .
12.通过平移将点A(-7,6)移到点A'(-2,2),若按同样的方式移动点B(3,1)到点B',则点B'的坐标是 .
13.已知点P(a-1,|a|-3)在x轴的负半轴上,则点P的坐标 .
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫作整点.如图,已知点A(0,4),点B是x轴正半轴上的整点,记三角形AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示).
三、解答题(共58分)
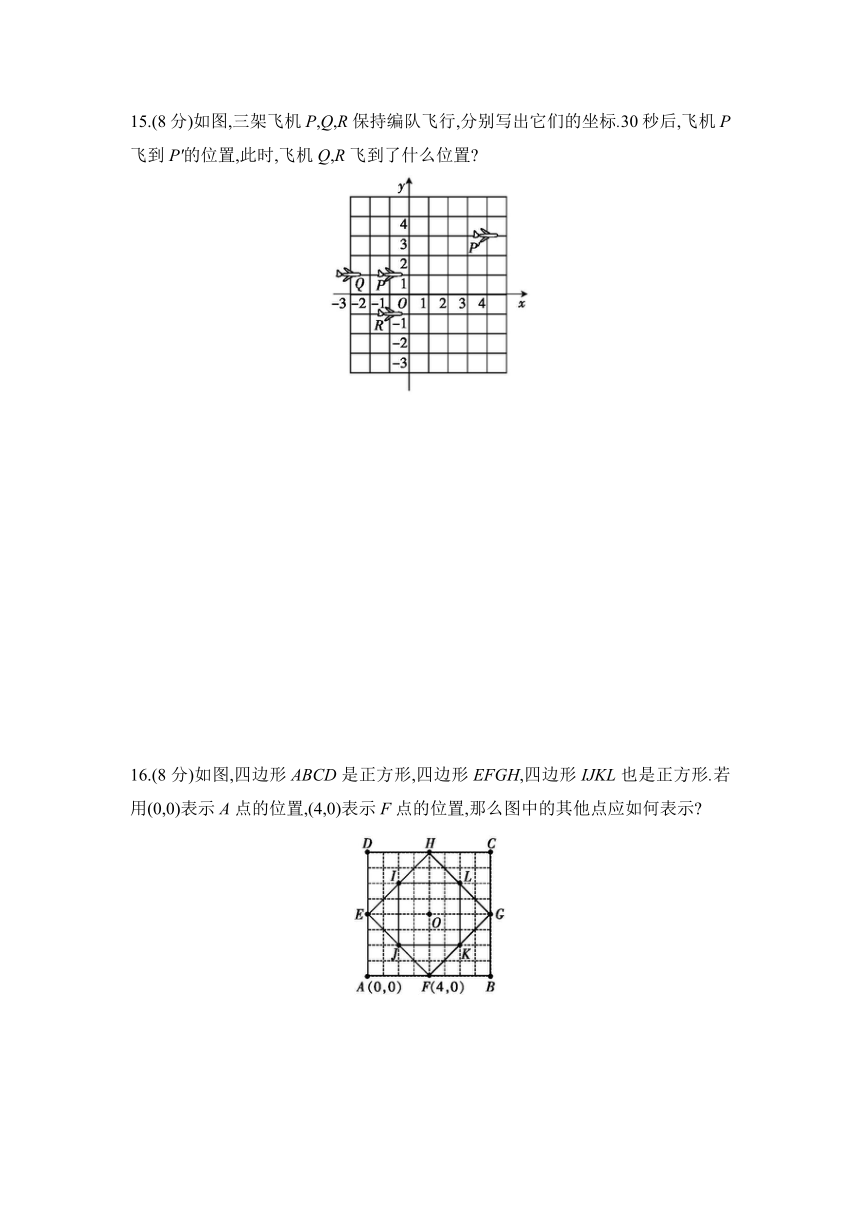
15.(8分)如图,三架飞机P,Q,R保持编队飞行,分别写出它们的坐标.30秒后,飞机P飞到P'的位置,此时,飞机Q,R飞到了什么位置
16.(8分)如图,四边形ABCD是正方形,四边形EFGH,四边形IJKL也是正方形.若用(0,0)表示A点的位置,(4,0)表示F点的位置,那么图中的其他点应如何表示
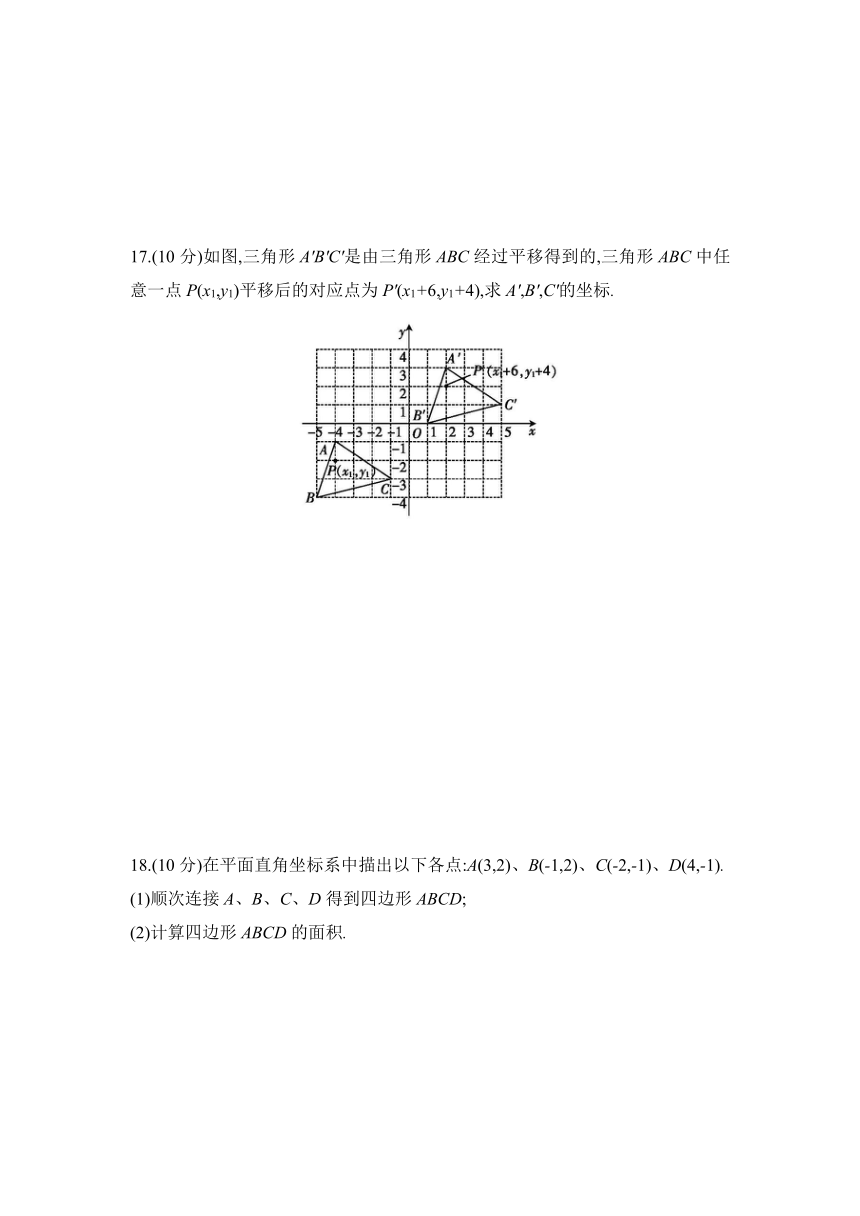
17.(10分)如图,三角形A'B'C'是由三角形ABC经过平移得到的,三角形ABC中任意一点P(x1,y1)平移后的对应点为P'(x1+6,y1+4),求A',B',C'的坐标.
18.(10分)在平面直角坐标系中描出以下各点:A(3,2)、B(-1,2)、C(-2,-1)、D(4,-1).
(1)顺次连接A、B、C、D得到四边形ABCD;
(2)计算四边形ABCD的面积.
19.(10分)如图,在网格中有点A(3,-1).
(1)将点A向左平移4个单位长度,得到点A1,请在图上标出这个点,并写出它的坐标;
(2)将点A向上平移4个单位长度,得到点A2,请在图上标出这个点,并写出它的坐标;
(3)你能判断直线AA1与x轴,直线AA2与y轴的位置关系吗
20.(12分)如图,在平面直角坐标系xOy中,A(4,0),C(0,6),B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即沿着O→A→B→C→O的路线移动).
(1)写出B点的坐标 ;
(2)当点P移动了4秒时,描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
参考答案
1.C 2.A 3.A 4.B 5.C 6.D 7.C 8.C
9.4
10.(2,-3)
11.4
12.(8,-3)
13.(-4,0)
14.3或4 6n-3
15.解:P(-1,1),Q(-3,1),R(-1,-1),30秒后飞机Q的位置为(2,3),飞机R的位置为(4,1).
16.解:B(8,0),C(8,8),D(0,8),E(0,4),G(8,4),H(4,8),I(2,6),J(2,2),K(6,2),L(6,6),O(4,4).
17.解:由图知A(-4,-1),B(-5,-4),C(-1,-3),因为点P(x1,y1)平移后变为P'(x1+6,y1+4),所以A'(2,3),B'(1,0),C'(5,1).
18.解:(1)先描点A、B、C、D,再顺次连接(图略);
(2)四边形ABCD为梯形,面积为15.
19.解:(1)如图,A1(-1,-1).
(2)如图,A2(3,3).
(3)直线AA1∥x轴,直线AA2∥y轴.
20.解:(1)(4,6).
(2)由每秒2个单位长度的速度沿着长方形OABC移动一周(即沿着O→A→B→C→O的路线移动),点P移动了4秒,得P点移动了8个单位,即OA+AP=8,
点P在AB上且距A点4个单位处,P(4,4).
(3)第一次距x轴5个单位时,AP=5,即OA+AP=9=2t,解得t=,
第二次距x轴5个单位时,OP=5,即OA+AB+BC+CP=4+6+4+6-5=2t,解得t=,
综上所述,当t=秒或t=秒时,点P到x轴的距离为5个单位长度.
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.已知点A(0,a)到x轴的距离是3,则a为 ( )
A.3 B.-3 C.±3 D.±6
2.若P(m,n)是第三象限内的点,则点Q(-n,0)在 ( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
3.中国象棋的一盘残局如图所示,如果用(4,0)表示“帥”的位置,用(3,9)表示“将”的位置,那么“炮”的位置应表示为 ( )
A.(8,7) B.(7,8)
C.(8,9) D.(8,8)
4.点A(m+3,m+1)在x轴上,则A点的坐标为 ( )
A.(0,-2) B.(2,0)
C.(4,0) D.(0,-4)
5.无论m取什么实数,点(-1,-m2-1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.点P在第二象限,并且到x轴的距离为1,到y轴的距离为3,那么点P的坐标为 ( )
A.(-1,3) B.(-1,-3)
C.(-3,-1) D.(-3,1)
7.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 ( )
A.(2,9) B.(5,3)
C.(1,2) D.(-9,-4)
8.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…,表示,则顶点A55的坐标是 ( )
A.(13,13) B.(-13,-13)
C.(14,14) D.(-14,-14)
二、填空题(每题3分,共18分)
9.已知点P(3,-4),它到x轴的距离是 .
10.设点P(x,y)在第四象限,且x2=4,|y|=3,则点P的坐标为 .
11.若点A(x,4-2x)在第二、四象限夹角的平分线上,则x= .
12.通过平移将点A(-7,6)移到点A'(-2,2),若按同样的方式移动点B(3,1)到点B',则点B'的坐标是 .
13.已知点P(a-1,|a|-3)在x轴的负半轴上,则点P的坐标 .
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫作整点.如图,已知点A(0,4),点B是x轴正半轴上的整点,记三角形AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示).
三、解答题(共58分)
15.(8分)如图,三架飞机P,Q,R保持编队飞行,分别写出它们的坐标.30秒后,飞机P飞到P'的位置,此时,飞机Q,R飞到了什么位置
16.(8分)如图,四边形ABCD是正方形,四边形EFGH,四边形IJKL也是正方形.若用(0,0)表示A点的位置,(4,0)表示F点的位置,那么图中的其他点应如何表示
17.(10分)如图,三角形A'B'C'是由三角形ABC经过平移得到的,三角形ABC中任意一点P(x1,y1)平移后的对应点为P'(x1+6,y1+4),求A',B',C'的坐标.
18.(10分)在平面直角坐标系中描出以下各点:A(3,2)、B(-1,2)、C(-2,-1)、D(4,-1).
(1)顺次连接A、B、C、D得到四边形ABCD;
(2)计算四边形ABCD的面积.
19.(10分)如图,在网格中有点A(3,-1).
(1)将点A向左平移4个单位长度,得到点A1,请在图上标出这个点,并写出它的坐标;
(2)将点A向上平移4个单位长度,得到点A2,请在图上标出这个点,并写出它的坐标;
(3)你能判断直线AA1与x轴,直线AA2与y轴的位置关系吗
20.(12分)如图,在平面直角坐标系xOy中,A(4,0),C(0,6),B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即沿着O→A→B→C→O的路线移动).
(1)写出B点的坐标 ;
(2)当点P移动了4秒时,描出此时点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
参考答案
1.C 2.A 3.A 4.B 5.C 6.D 7.C 8.C
9.4
10.(2,-3)
11.4
12.(8,-3)
13.(-4,0)
14.3或4 6n-3
15.解:P(-1,1),Q(-3,1),R(-1,-1),30秒后飞机Q的位置为(2,3),飞机R的位置为(4,1).
16.解:B(8,0),C(8,8),D(0,8),E(0,4),G(8,4),H(4,8),I(2,6),J(2,2),K(6,2),L(6,6),O(4,4).
17.解:由图知A(-4,-1),B(-5,-4),C(-1,-3),因为点P(x1,y1)平移后变为P'(x1+6,y1+4),所以A'(2,3),B'(1,0),C'(5,1).
18.解:(1)先描点A、B、C、D,再顺次连接(图略);
(2)四边形ABCD为梯形,面积为15.
19.解:(1)如图,A1(-1,-1).
(2)如图,A2(3,3).
(3)直线AA1∥x轴,直线AA2∥y轴.
20.解:(1)(4,6).
(2)由每秒2个单位长度的速度沿着长方形OABC移动一周(即沿着O→A→B→C→O的路线移动),点P移动了4秒,得P点移动了8个单位,即OA+AP=8,
点P在AB上且距A点4个单位处,P(4,4).
(3)第一次距x轴5个单位时,AP=5,即OA+AP=9=2t,解得t=,
第二次距x轴5个单位时,OP=5,即OA+AB+BC+CP=4+6+4+6-5=2t,解得t=,
综上所述,当t=秒或t=秒时,点P到x轴的距离为5个单位长度.
