【课时作业】第12章 一次函数 测试卷(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第12章 一次函数 测试卷(含答案)2024-2025学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览


文档简介
第12章 一次函数 测试卷
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.若正比例函数y=kx经过点(1,2),则k的值为 ( )
A.- B.-2 C. D.2
2.已知两个变量x和y之间的 3组对应值如下表所示:
x -1 0 1
y -1 1 3
则y与x之间的函数表达式可能是 ( )
A.y=x B.y=2x+1
C.y=x2+x+1 D.y=
3.已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是 ( )
A.x<0
B.-12
C.x>-1
D.x<-1或14.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图象上的两点,则a与b的大小关系是 ( )
A.a>b B.a=b
C.a5.已知点(-2,y1)和(4,y2)都在直线y=(k-5)x+4上,若y1A.k>0 B.k<0 C.k>5 D.k<5
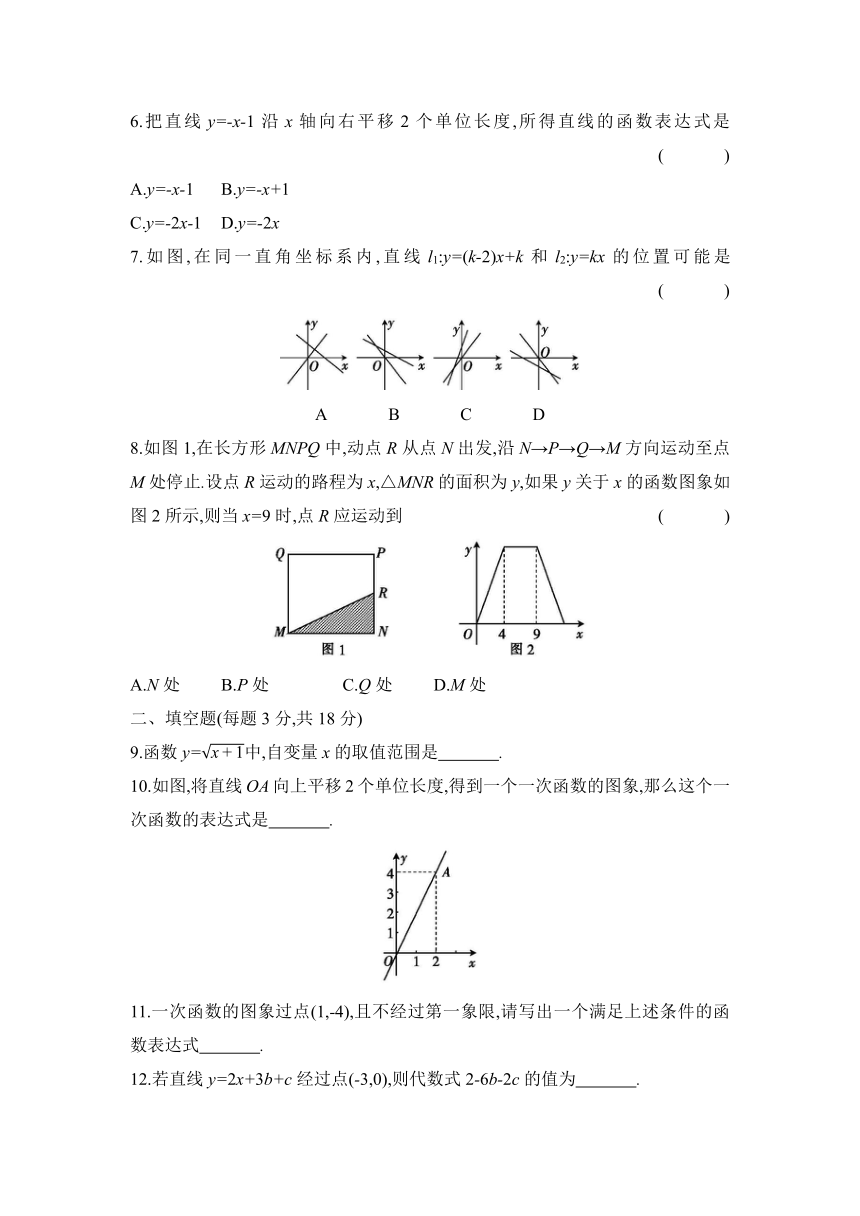
6.把直线y=-x-1沿x轴向右平移2个单位长度,所得直线的函数表达式是 ( )
A.y=-x-1 B.y=-x+1
C.y=-2x-1 D.y=-2x
7.如图,在同一直角坐标系内,直线l1:y=(k-2)x+k和l2:y=kx的位置可能是 ( )
A B C D
8.如图1,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 ( )
A.N处 B.P处 C.Q处 D.M处
二、填空题(每题3分,共18分)
9.函数y=中,自变量x的取值范围是 .
10.如图,将直线OA向上平移2个单位长度,得到一个一次函数的图象,那么这个一次函数的表达式是 .
11.一次函数的图象过点(1,-4),且不经过第一象限,请写出一个满足上述条件的函数表达式 .
12.若直线y=2x+3b+c经过点(-3,0),则代数式2-6b-2c的值为 .
13.某汽车的油箱容量为60 L,加满汽油后行驶了100 km时,油箱中的汽油消耗了,若加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数表达式是 .
14.甲、乙两人驾车从A地出发匀速行驶到B地,在整个行驶过程中,甲、乙离开A地的距离y(千米)与行驶的时间t(时)之间的函数关系如图所示,有下列结论:
①A、B两地相距300千米;
②乙比甲晚出发1小时,早到1小时;
③乙车出发2.5小时后追上甲车;
④当甲、乙两人相距50千米时,t=或.
其中正确的是 .(把所有正确结论的序号都填在横线上)
三、解答题(共58分)
15.(8分)已知一次函数y=kx+b的图象平行于直线y=-2x,且过点A(-4,2),求此函数表达式.
16.(10分)已知一次函数的图象经过点A(0,2)且与坐标轴围成的直角三角形面积为8,求这个一次函数的表达式.
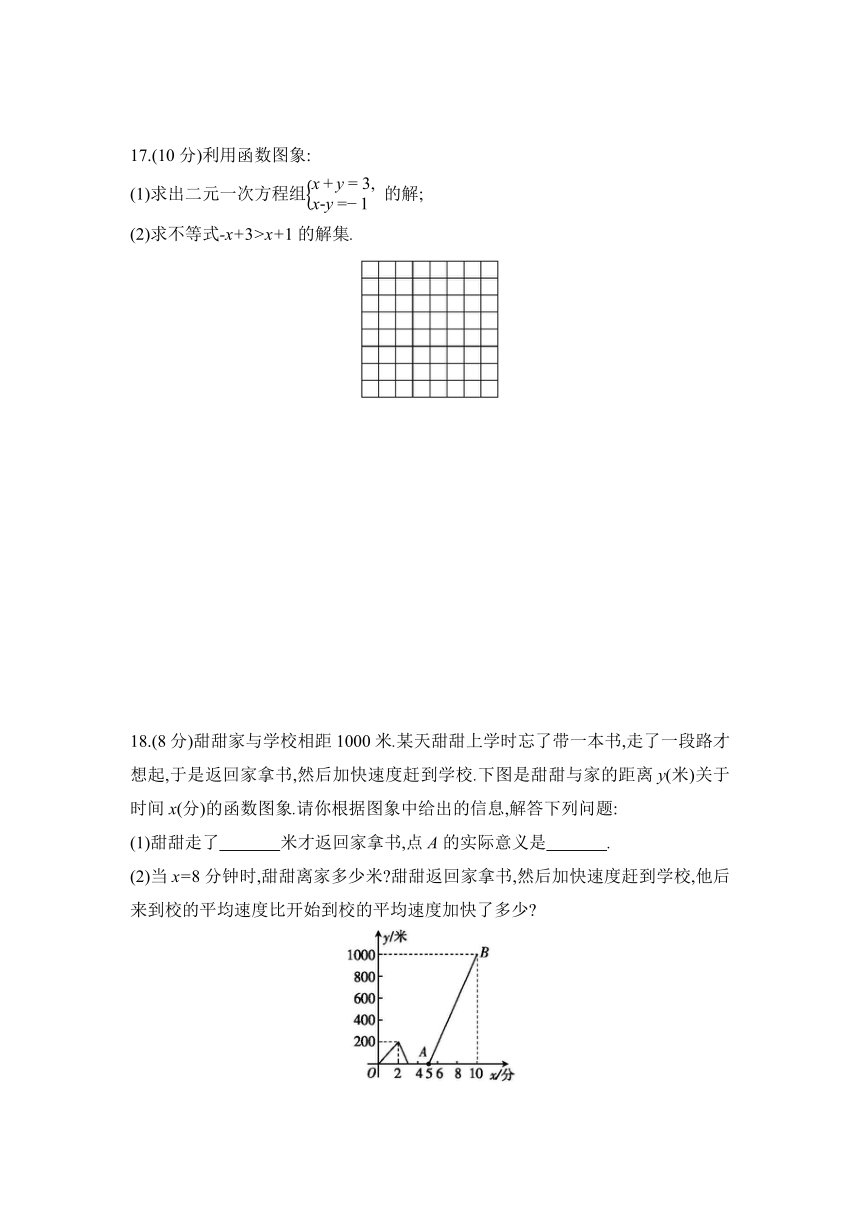
17.(10分)利用函数图象:
(1)求出二元一次方程组 的解;
(2)求不等式-x+3>x+1的解集.
18.(8分)甜甜家与学校相距1000米.某天甜甜上学时忘了带一本书,走了一段路才想起,于是返回家拿书,然后加快速度赶到学校.下图是甜甜与家的距离y(米)关于时间x(分)的函数图象.请你根据图象中给出的信息,解答下列问题:
(1)甜甜走了 米才返回家拿书,点A的实际意义是 .
(2)当x=8分钟时,甜甜离家多少米 甜甜返回家拿书,然后加快速度赶到学校,他后来到校的平均速度比开始到校的平均速度加快了多少
19.(10分)观察图形,解决问题:
(1)图⑩中黑色正方形的个数是 ,白色正方形的个数是 ;
(2)设第x个图中黑色正方形的个数为y1,白色正方形的个数为y2,求y1、y2与x之间的函数表达式;
(3)是否存在这样的图形,图中黑色正方形的个数和白色正方形的个数相等 若存在,请指出是第几个图;若不存在,说明你的理由.
20.(12分)某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10 L时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185 min才能将这批工件加工完.下图中的折线OAB是油箱中油量y(L)与机器运行时间x(min)之间的函数关系图象,根据图象解决以下问题:
(1) 函数图象中描述机器加油过程的是 (填OA或AB);
(2)求第一个加工过程中,油箱中油量y(L)与机器运行时间x(min)之间的函数表达式(不要求写出自变量x的取值范围),并求出机器运行多少分钟时,第一个加工过程停止;
(3)加工完这批工件,机器耗油多少升
参考答案
1.D 2.B 3.B 4.A 5.C 6.B 7.A 8.C
9.x≥-1
10.y=2x+2
11.答案不唯一如:y=-4x,y=-x-3,等等
12.-10
13.y=60-0.12x(0≤x≤500)
14.①②④
15.解:因为所求直线平行于直线y=-2x,所以k=-2,
可设y=-2x+b,将(-4,2)代入,所以b=-6,
所以函数表达式为y=-2x-6.
16.解:因为函数的图象经过点A(0,2),所以可设一次函数表达式为y=kx+2,
由kx+2=0,解得x=-,即图象与x轴的交点坐标为-,0,
由三角形的面积公式得×-×2=8,解得k=±,所以这个一次函数的表达式为y=x+2或y=-x+2.
17.解:(1)图略.
两条直线的交点坐标为P(1,2),
所以方程组的解为
(2)由图象可知,两条直线的交点坐标为P(1,2),
当x<1时,直线y=-x+3在直线y=x+1的上方,
所以不等式-x+3>x+1的解集为x<1.
18.解:(1)200;点A的实际意义是甜甜找到书再次从家出发的时间.
(2)设直线AB函数表达式为y=kx+b,
由图可知图象过(5,0),(10,1000)两点,
可得解得
直线AB函数表达式为y=200x-1000.
当x=8分钟时,y=200×8-1000=600.
此时甜甜离家为600米.
平均速度加快为-=100(米/分).
19.解:(1)29;28.
(2)y1=2+3(x-1),y2=1+3(x-1).
(3)不存在,因为方程2+3(x-1)=1+3(x-1)无解.
20.解:(1)OA.
(2)因为加工过程需要耗油,观察图象可知AB为机器第一个加工过程,符合一次函数关系,且(10,100),(30,80)在一次函数的图象上,设油箱中油量y(L)与机器运行时间x(min)之间的函数表达式为y=kx+b,
所以有解得
所以y=-x+110.
当第一个加工过程停止时,油箱中剩油量为10升,将y=10代入y=-x+110得10=-x+110,解得x=100,
所以机器运行100分钟后,第一个加工过程停止.
(3)由(2)知机器运行100分钟后,第一个加工过程停止,此时油箱剩10升,说明90分钟(机器运行100分钟,内含10分钟的加油时间)耗油100-10=90升,也就是每分钟机器耗油1升,又加工完这批工件机器需运行185 min,说明机器第2次运行了185-100-9=76 min(其中9分钟是第1个加工过程停止后再加满油所用时间,从图象上可知每分钟加油=10升,第2次需加油100-10=90升),所以第2次加工过程耗油1×76=76升,
故加工完这批工件,机器共耗油90+76=166(升).
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.若正比例函数y=kx经过点(1,2),则k的值为 ( )
A.- B.-2 C. D.2
2.已知两个变量x和y之间的 3组对应值如下表所示:
x -1 0 1
y -1 1 3
则y与x之间的函数表达式可能是 ( )
A.y=x B.y=2x+1
C.y=x2+x+1 D.y=
3.已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是 ( )
A.x<0
B.-1
C.x>-1
D.x<-1或1
A.a>b B.a=b
C.a5.已知点(-2,y1)和(4,y2)都在直线y=(k-5)x+4上,若y1
6.把直线y=-x-1沿x轴向右平移2个单位长度,所得直线的函数表达式是 ( )
A.y=-x-1 B.y=-x+1
C.y=-2x-1 D.y=-2x
7.如图,在同一直角坐标系内,直线l1:y=(k-2)x+k和l2:y=kx的位置可能是 ( )
A B C D
8.如图1,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 ( )
A.N处 B.P处 C.Q处 D.M处
二、填空题(每题3分,共18分)
9.函数y=中,自变量x的取值范围是 .
10.如图,将直线OA向上平移2个单位长度,得到一个一次函数的图象,那么这个一次函数的表达式是 .
11.一次函数的图象过点(1,-4),且不经过第一象限,请写出一个满足上述条件的函数表达式 .
12.若直线y=2x+3b+c经过点(-3,0),则代数式2-6b-2c的值为 .
13.某汽车的油箱容量为60 L,加满汽油后行驶了100 km时,油箱中的汽油消耗了,若加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数表达式是 .
14.甲、乙两人驾车从A地出发匀速行驶到B地,在整个行驶过程中,甲、乙离开A地的距离y(千米)与行驶的时间t(时)之间的函数关系如图所示,有下列结论:
①A、B两地相距300千米;
②乙比甲晚出发1小时,早到1小时;
③乙车出发2.5小时后追上甲车;
④当甲、乙两人相距50千米时,t=或.
其中正确的是 .(把所有正确结论的序号都填在横线上)
三、解答题(共58分)
15.(8分)已知一次函数y=kx+b的图象平行于直线y=-2x,且过点A(-4,2),求此函数表达式.
16.(10分)已知一次函数的图象经过点A(0,2)且与坐标轴围成的直角三角形面积为8,求这个一次函数的表达式.
17.(10分)利用函数图象:
(1)求出二元一次方程组 的解;
(2)求不等式-x+3>x+1的解集.
18.(8分)甜甜家与学校相距1000米.某天甜甜上学时忘了带一本书,走了一段路才想起,于是返回家拿书,然后加快速度赶到学校.下图是甜甜与家的距离y(米)关于时间x(分)的函数图象.请你根据图象中给出的信息,解答下列问题:
(1)甜甜走了 米才返回家拿书,点A的实际意义是 .
(2)当x=8分钟时,甜甜离家多少米 甜甜返回家拿书,然后加快速度赶到学校,他后来到校的平均速度比开始到校的平均速度加快了多少
19.(10分)观察图形,解决问题:
(1)图⑩中黑色正方形的个数是 ,白色正方形的个数是 ;
(2)设第x个图中黑色正方形的个数为y1,白色正方形的个数为y2,求y1、y2与x之间的函数表达式;
(3)是否存在这样的图形,图中黑色正方形的个数和白色正方形的个数相等 若存在,请指出是第几个图;若不存在,说明你的理由.
20.(12分)某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10 L时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185 min才能将这批工件加工完.下图中的折线OAB是油箱中油量y(L)与机器运行时间x(min)之间的函数关系图象,根据图象解决以下问题:
(1) 函数图象中描述机器加油过程的是 (填OA或AB);
(2)求第一个加工过程中,油箱中油量y(L)与机器运行时间x(min)之间的函数表达式(不要求写出自变量x的取值范围),并求出机器运行多少分钟时,第一个加工过程停止;
(3)加工完这批工件,机器耗油多少升
参考答案
1.D 2.B 3.B 4.A 5.C 6.B 7.A 8.C
9.x≥-1
10.y=2x+2
11.答案不唯一如:y=-4x,y=-x-3,等等
12.-10
13.y=60-0.12x(0≤x≤500)
14.①②④
15.解:因为所求直线平行于直线y=-2x,所以k=-2,
可设y=-2x+b,将(-4,2)代入,所以b=-6,
所以函数表达式为y=-2x-6.
16.解:因为函数的图象经过点A(0,2),所以可设一次函数表达式为y=kx+2,
由kx+2=0,解得x=-,即图象与x轴的交点坐标为-,0,
由三角形的面积公式得×-×2=8,解得k=±,所以这个一次函数的表达式为y=x+2或y=-x+2.
17.解:(1)图略.
两条直线的交点坐标为P(1,2),
所以方程组的解为
(2)由图象可知,两条直线的交点坐标为P(1,2),
当x<1时,直线y=-x+3在直线y=x+1的上方,
所以不等式-x+3>x+1的解集为x<1.
18.解:(1)200;点A的实际意义是甜甜找到书再次从家出发的时间.
(2)设直线AB函数表达式为y=kx+b,
由图可知图象过(5,0),(10,1000)两点,
可得解得
直线AB函数表达式为y=200x-1000.
当x=8分钟时,y=200×8-1000=600.
此时甜甜离家为600米.
平均速度加快为-=100(米/分).
19.解:(1)29;28.
(2)y1=2+3(x-1),y2=1+3(x-1).
(3)不存在,因为方程2+3(x-1)=1+3(x-1)无解.
20.解:(1)OA.
(2)因为加工过程需要耗油,观察图象可知AB为机器第一个加工过程,符合一次函数关系,且(10,100),(30,80)在一次函数的图象上,设油箱中油量y(L)与机器运行时间x(min)之间的函数表达式为y=kx+b,
所以有解得
所以y=-x+110.
当第一个加工过程停止时,油箱中剩油量为10升,将y=10代入y=-x+110得10=-x+110,解得x=100,
所以机器运行100分钟后,第一个加工过程停止.
(3)由(2)知机器运行100分钟后,第一个加工过程停止,此时油箱剩10升,说明90分钟(机器运行100分钟,内含10分钟的加油时间)耗油100-10=90升,也就是每分钟机器耗油1升,又加工完这批工件机器需运行185 min,说明机器第2次运行了185-100-9=76 min(其中9分钟是第1个加工过程停止后再加满油所用时间,从图象上可知每分钟加油=10升,第2次需加油100-10=90升),所以第2次加工过程耗油1×76=76升,
故加工完这批工件,机器共耗油90+76=166(升).
