【课时作业】第13章 三角形中的边角关系、命题与证明 测试卷(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第13章 三角形中的边角关系、命题与证明 测试卷(含答案)2024-2025学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 103.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览



文档简介
第13章 三角形中的边角关系、命题与证明 测试卷
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.一位同学用三根木棒拼成的图形如下,则其中符合三角形的是 ( )
A B C D
2.三角形的三边分别为3,1-2a,8,则a的取值范围是 ( )
A.-6B.-5C.2D.a<-5或a>-2
3.如果三角形的一个内角等于其他两个内角的差,那么这个三角形是 ( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.斜三角形
4.下列命题中,是真命题的是 ( )
A.三角形的一个外角大于任何一个内角
B.三角形的一个外角等于两个内角之和
C.三角形的两边之和一定不小于第三边
D.三角形的三条中线交于一点,这个交点就是三角形的重心
5.将一副直角三角尺按如图所示的方式放置,若∠AOD=20°,则∠BOC的大小为 ( )
A.140° B.160°
C.170° D.150°
6.一个三角形的两个内角相等,且一个外角等于110°,则这个三角形的底角为 ( )
A.55° B.70°
C.55°或70° D.无法求解
7.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为 ( )
A.2 B.3 C.5 D.13
8.如图,在△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是 ( )
A.25
B.30
C.35
D.40
二、填空题(每题3分,共18分)
9.命题“有两个角互余的三角形是直角三角形”的逆命题是 .
10.一个承重架的结构如图所示,如果∠1=155°,那么∠2= 度.
11.在△ABC中,三个内角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B= 度.
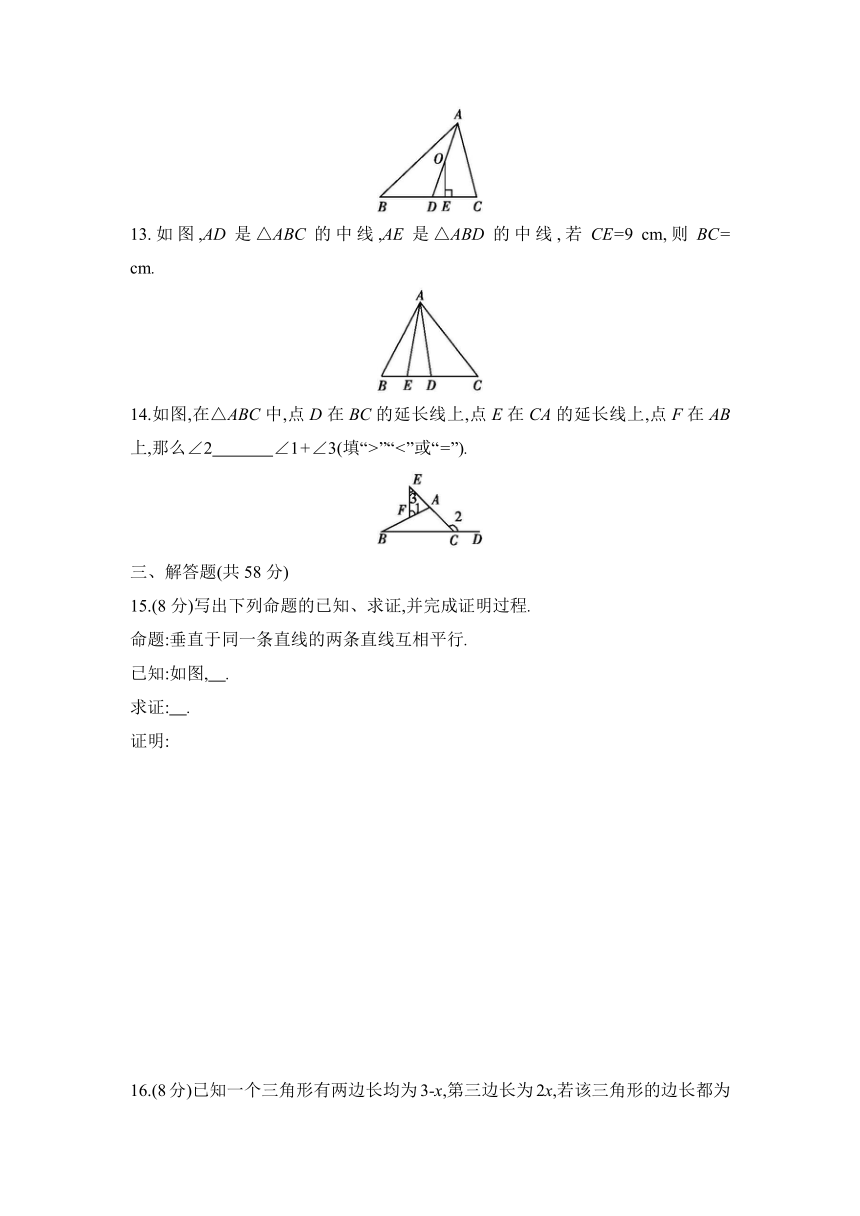
12.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为 .
13.如图,AD是△ABC的中线,AE是△ABD的中线,若CE=9 cm,则BC= cm.
14.如图,在△ABC中,点D在BC的延长线上,点E在CA的延长线上,点F在AB上,那么∠2 ∠1+∠3(填“>”“<”或“=”).
三、解答题(共58分)
15.(8分)写出下列命题的已知、求证,并完成证明过程.
命题:垂直于同一条直线的两条直线互相平行.
已知:如图, .
求证: .
证明:
16.(8分)已知一个三角形有两边长均为3-x,第三边长为2x,若该三角形的边长都为整数,试判断此三角形的形状.
17.(10分)如图,在△ABC中,AB=AC,AC上的中线把三角形的周长分为24 cm和30 cm的两个部分,求三角形各边的长.
18.(10分)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于点E、F,求证:∠CEF=∠CFE.
19.(10分)在长方形台球桌上选择适当的方向击打白球,使白球两次撞击桌面边缘后将红球撞入袋中,此时,∠1=∠2,∠3=∠4(如图).
求证:白球第二次反弹后的方向与开始击打白球方向平行,即AB∥CD.
20.(12分)如图①,在△ABC中,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACE=110°,求∠D的度数;
(2)若∠A=78°,求∠D的度数;若∠A=α°,直接写出∠D的度数;
(3)如图②,∠ABC的平分线与∠ACE的平分线交于点D1,∠D1BC的平分线与∠D1CE的平分线交于点D2,…,∠Dn-1BC的平分线与∠Dn-1CE的平分线交于点Dn.若∠A=α°,则∠Dn= .
参考答案
1.A 2.B 3.C 4.D 5.B 6.C 7.B 8.B
9.直角三角形有两个角互余
10.65
11.60
12.20°
13.12
14.>
15.已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D.
求证:AB∥CD.
证明:因为AB⊥EF,垂足为B,CD⊥EF,垂足为D( 已知),
所以∠ABD=∠CDF=90° (垂直的定义),
所以AB∥CD (同位角相等,两直线平行).
16.解:根据三角形的三边关系得
(3-x)-(3-x)<2x<(3-x)+(3-x),
0<2x<6-2x,0因为2x是正整数,所以x=1.
所以三角形的三边长分别是2、2、2,
因此,该三角形是等边三角形.
17.解:设AB=AC=2x,则AD=CD=x,
(1)当AB+AD=30,BC+CD=24时,有2x+x=30,
∴x=10,2x=20,BC=24-10=14,三角形的三边分别为20 cm,20 cm,14 cm.
(2)当AB+AD=24,BC+CD=30时,有2x+x=24,
∴x=8,BC=30-8=22,三边分别为16 cm,16 cm,22 cm.
18.证明:(1)∵∠ACB=90°,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B.
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理,在Rt△AED中,∠AED=90°-∠DAE,
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE.
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
19.证明:∵∠1=∠2,∠3=∠4,
∠1+∠2+∠ABD=∠3+∠4+∠BDC=180°,
∴2∠2+∠ABD+2∠3+∠BDC=360°.①
∵∠2+∠3+∠E=180°,∴∠2+∠3=90°.
将∠2+∠3=90°代入①,得
180°+∠ABD+∠BDC=360°,
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补,两直线平行).
20.解:(1)因为BD平分∠ABC,CD平分∠ACE,
∠DBC =∠ABC=×60°=30°,
∠DCE=∠ACE=×110°=55°,
由三角形内角和定理推论有∠D=55°-30°=25°.
(2)在△ABC中,∠ABC=∠ACE-78°,所以∠ABC=(∠ACE-78°),
∠ABC+∠D=∠ACE,
有(∠ACE-78°)+∠D=∠ACE,∠D==39°,
若∠A=α°,则∠D=α°.
(3)∠Dn=.
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.一位同学用三根木棒拼成的图形如下,则其中符合三角形的是 ( )
A B C D
2.三角形的三边分别为3,1-2a,8,则a的取值范围是 ( )
A.-6
3.如果三角形的一个内角等于其他两个内角的差,那么这个三角形是 ( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.斜三角形
4.下列命题中,是真命题的是 ( )
A.三角形的一个外角大于任何一个内角
B.三角形的一个外角等于两个内角之和
C.三角形的两边之和一定不小于第三边
D.三角形的三条中线交于一点,这个交点就是三角形的重心
5.将一副直角三角尺按如图所示的方式放置,若∠AOD=20°,则∠BOC的大小为 ( )
A.140° B.160°
C.170° D.150°
6.一个三角形的两个内角相等,且一个外角等于110°,则这个三角形的底角为 ( )
A.55° B.70°
C.55°或70° D.无法求解
7.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为 ( )
A.2 B.3 C.5 D.13
8.如图,在△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是 ( )
A.25
B.30
C.35
D.40
二、填空题(每题3分,共18分)
9.命题“有两个角互余的三角形是直角三角形”的逆命题是 .
10.一个承重架的结构如图所示,如果∠1=155°,那么∠2= 度.
11.在△ABC中,三个内角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B= 度.
12.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为 .
13.如图,AD是△ABC的中线,AE是△ABD的中线,若CE=9 cm,则BC= cm.
14.如图,在△ABC中,点D在BC的延长线上,点E在CA的延长线上,点F在AB上,那么∠2 ∠1+∠3(填“>”“<”或“=”).
三、解答题(共58分)
15.(8分)写出下列命题的已知、求证,并完成证明过程.
命题:垂直于同一条直线的两条直线互相平行.
已知:如图, .
求证: .
证明:
16.(8分)已知一个三角形有两边长均为3-x,第三边长为2x,若该三角形的边长都为整数,试判断此三角形的形状.
17.(10分)如图,在△ABC中,AB=AC,AC上的中线把三角形的周长分为24 cm和30 cm的两个部分,求三角形各边的长.
18.(10分)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于点E、F,求证:∠CEF=∠CFE.
19.(10分)在长方形台球桌上选择适当的方向击打白球,使白球两次撞击桌面边缘后将红球撞入袋中,此时,∠1=∠2,∠3=∠4(如图).
求证:白球第二次反弹后的方向与开始击打白球方向平行,即AB∥CD.
20.(12分)如图①,在△ABC中,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACE=110°,求∠D的度数;
(2)若∠A=78°,求∠D的度数;若∠A=α°,直接写出∠D的度数;
(3)如图②,∠ABC的平分线与∠ACE的平分线交于点D1,∠D1BC的平分线与∠D1CE的平分线交于点D2,…,∠Dn-1BC的平分线与∠Dn-1CE的平分线交于点Dn.若∠A=α°,则∠Dn= .
参考答案
1.A 2.B 3.C 4.D 5.B 6.C 7.B 8.B
9.直角三角形有两个角互余
10.65
11.60
12.20°
13.12
14.>
15.已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D.
求证:AB∥CD.
证明:因为AB⊥EF,垂足为B,CD⊥EF,垂足为D( 已知),
所以∠ABD=∠CDF=90° (垂直的定义),
所以AB∥CD (同位角相等,两直线平行).
16.解:根据三角形的三边关系得
(3-x)-(3-x)<2x<(3-x)+(3-x),
0<2x<6-2x,0
所以三角形的三边长分别是2、2、2,
因此,该三角形是等边三角形.
17.解:设AB=AC=2x,则AD=CD=x,
(1)当AB+AD=30,BC+CD=24时,有2x+x=30,
∴x=10,2x=20,BC=24-10=14,三角形的三边分别为20 cm,20 cm,14 cm.
(2)当AB+AD=24,BC+CD=30时,有2x+x=24,
∴x=8,BC=30-8=22,三边分别为16 cm,16 cm,22 cm.
18.证明:(1)∵∠ACB=90°,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B.
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理,在Rt△AED中,∠AED=90°-∠DAE,
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE.
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
19.证明:∵∠1=∠2,∠3=∠4,
∠1+∠2+∠ABD=∠3+∠4+∠BDC=180°,
∴2∠2+∠ABD+2∠3+∠BDC=360°.①
∵∠2+∠3+∠E=180°,∴∠2+∠3=90°.
将∠2+∠3=90°代入①,得
180°+∠ABD+∠BDC=360°,
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补,两直线平行).
20.解:(1)因为BD平分∠ABC,CD平分∠ACE,
∠DBC =∠ABC=×60°=30°,
∠DCE=∠ACE=×110°=55°,
由三角形内角和定理推论有∠D=55°-30°=25°.
(2)在△ABC中,∠ABC=∠ACE-78°,所以∠ABC=(∠ACE-78°),
∠ABC+∠D=∠ACE,
有(∠ACE-78°)+∠D=∠ACE,∠D==39°,
若∠A=α°,则∠D=α°.
(3)∠Dn=.
