【课时作业】第13章 三角形中的边角关系、命题与证明 复习课作业设计(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第13章 三角形中的边角关系、命题与证明 复习课作业设计(含答案)2024-2025学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 49.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览

文档简介
第13章 三角形中的边角关系、命题与证明 复习课作业设计
一、作业目标
1.了解三角形的元素与分类,掌握三角形的边角关系.
2.利用三角形的边角关系进行相关的计算.
3.知道命题、原命题、逆命题,真命题、假命题等相关概念.
4.掌握证明的基本格式,能够进行严谨的数学推理证明.
二、作业内容
【基础达标】
1若三角形的三边长分别是3,1-2m,8,则数m的取值范围是 ( )
A.-5B.-5C.5D.02下列命题是真命题的是 ( )
A.若a2=b2,则a=b
B.若ab=0,则b=0
C.三角形内角和是180°
D.三角形一条边的两个顶点到这条边上的中线所在直线的距离相等
3若等腰三角形的两边长分别是4和8,则这个三角形的周长是 .
4在△ABC中,
(1)若∠A∶∠B∶∠C=2∶3∶4,则∠C= °;
(2)若∠A=∠B=∠C,则∠B= °.
【能力巩固】
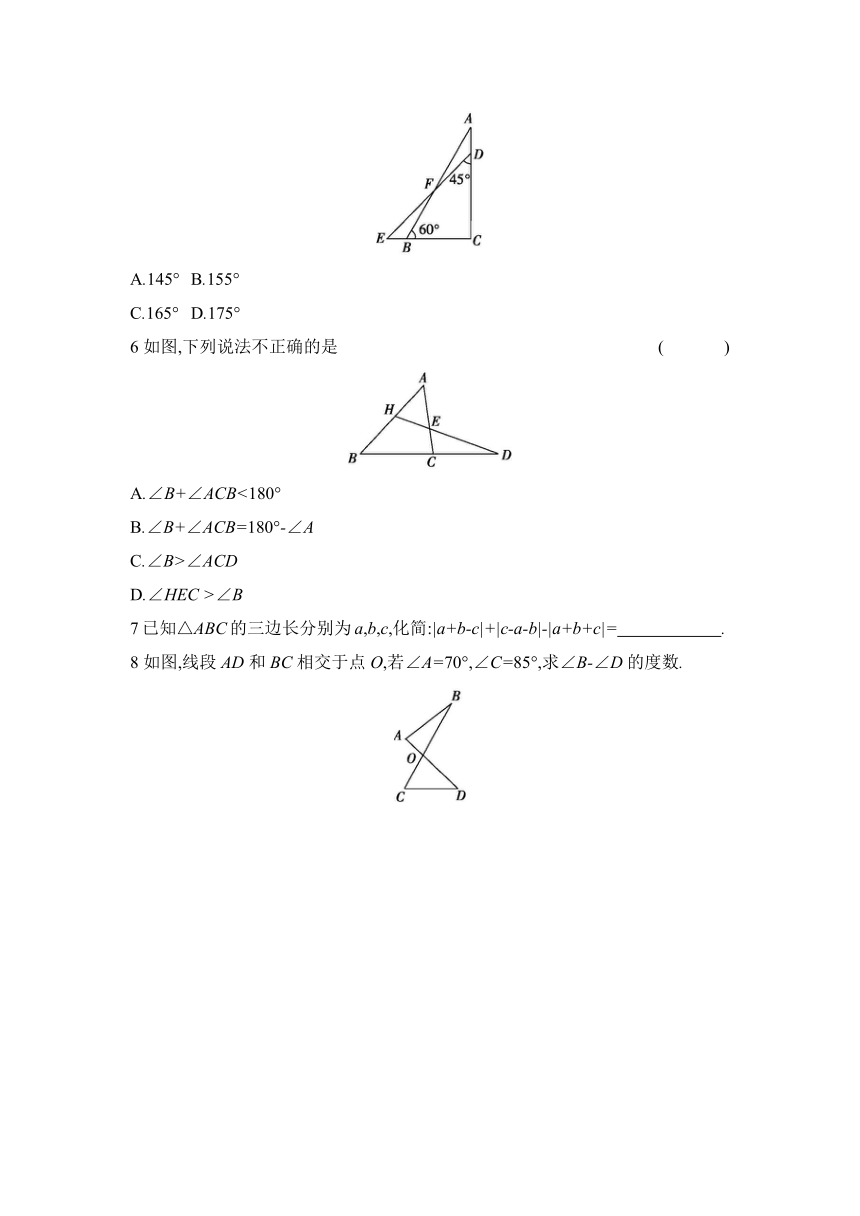
5将一副直角三角板按如图所示的方式放置,使两直角重合,则∠DFB的度数为 ( )
A.145° B.155°
C.165° D.175°
6如图,下列说法不正确的是 ( )
A.∠B+∠ACB<180°
B.∠B+∠ACB=180°-∠A
C.∠B>∠ACD
D.∠HEC >∠B
7已知△ABC的三边长分别为a,b,c,化简:|a+b-c|+|c-a-b|-|a+b+c|= .
8如图,线段AD和BC相交于点O,若∠A=70°,∠C=85°,求∠B-∠D的度数.
【素养拓展】
9(1)如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.求证:∠D=90°+∠A.
图1
(2)如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的数量关系.
(3)如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等数关系.
图2 图3
参考答案
1.A 2.C
3.20
4.(1)80
(2)60
5.C 6.C
7.a+b-3c
8.解:∵∠C+∠D+∠COD=180°,∠A+∠B+∠AOB=180°,
∴∠D=180°-∠C-∠COD,∠B=180°-∠A-∠AOB.
∵∠AOB=∠COD,
∴∠B-∠D=(180°-∠A-∠AOB)-(180°-∠C-∠COD)=∠C-∠A=85°-70°=15°,∴∠B-∠D=15°.
9.解:(1)证明:∵BD平分∠ABC,
∴∠1=∠ABC.同理,∠2=∠ACB.
∵∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,
∴∠D=180°-(∠ABC+∠ACB),
∴∠D=90°+∠A.
(2)∠D=90°-∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF.∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,而∠ABC=180°-2∠DBC,∠ACB=180°-2∠DCB,
∴∠A+180°-2∠DBC+180°-2∠DCB=180°,
∴∠A-2(∠DBC+∠DCB)=-180°,
∴∠A-2(180°-∠D)=-180°,
∴∠A+2∠D=180°,∴∠D=90°-∠A.
(3)∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D.
∵∠A+2∠DBC=2∠DCE,
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,∴∠D=∠A.
一、作业目标
1.了解三角形的元素与分类,掌握三角形的边角关系.
2.利用三角形的边角关系进行相关的计算.
3.知道命题、原命题、逆命题,真命题、假命题等相关概念.
4.掌握证明的基本格式,能够进行严谨的数学推理证明.
二、作业内容
【基础达标】
1若三角形的三边长分别是3,1-2m,8,则数m的取值范围是 ( )
A.-5
A.若a2=b2,则a=b
B.若ab=0,则b=0
C.三角形内角和是180°
D.三角形一条边的两个顶点到这条边上的中线所在直线的距离相等
3若等腰三角形的两边长分别是4和8,则这个三角形的周长是 .
4在△ABC中,
(1)若∠A∶∠B∶∠C=2∶3∶4,则∠C= °;
(2)若∠A=∠B=∠C,则∠B= °.
【能力巩固】
5将一副直角三角板按如图所示的方式放置,使两直角重合,则∠DFB的度数为 ( )
A.145° B.155°
C.165° D.175°
6如图,下列说法不正确的是 ( )
A.∠B+∠ACB<180°
B.∠B+∠ACB=180°-∠A
C.∠B>∠ACD
D.∠HEC >∠B
7已知△ABC的三边长分别为a,b,c,化简:|a+b-c|+|c-a-b|-|a+b+c|= .
8如图,线段AD和BC相交于点O,若∠A=70°,∠C=85°,求∠B-∠D的度数.
【素养拓展】
9(1)如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.求证:∠D=90°+∠A.
图1
(2)如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的数量关系.
(3)如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等数关系.
图2 图3
参考答案
1.A 2.C
3.20
4.(1)80
(2)60
5.C 6.C
7.a+b-3c
8.解:∵∠C+∠D+∠COD=180°,∠A+∠B+∠AOB=180°,
∴∠D=180°-∠C-∠COD,∠B=180°-∠A-∠AOB.
∵∠AOB=∠COD,
∴∠B-∠D=(180°-∠A-∠AOB)-(180°-∠C-∠COD)=∠C-∠A=85°-70°=15°,∴∠B-∠D=15°.
9.解:(1)证明:∵BD平分∠ABC,
∴∠1=∠ABC.同理,∠2=∠ACB.
∵∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,
∴∠D=180°-(∠ABC+∠ACB),
∴∠D=90°+∠A.
(2)∠D=90°-∠A.
理由:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF.∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,而∠ABC=180°-2∠DBC,∠ACB=180°-2∠DCB,
∴∠A+180°-2∠DBC+180°-2∠DCB=180°,
∴∠A-2(∠DBC+∠DCB)=-180°,
∴∠A-2(180°-∠D)=-180°,
∴∠A+2∠D=180°,∴∠D=90°-∠A.
(3)∠D=∠A.
理由:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∴∠DCE=∠DBC+∠D.
∵∠A+2∠DBC=2∠DCE,
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,∴∠D=∠A.
