【课时作业】第14章 全等三角形 测试卷(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第14章 全等三角形 测试卷(含答案)2024-2025学年数学沪科版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 211.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 21:33:22 | ||
图片预览


文档简介
第14章 全等三角形 测试卷
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.下列图形中与已知图形全等的是 ( )
A B C D
2.若△ABC与△DEF全等,A和D,B和E分别是对应点,则下列结论错误的是 ( )
A.∠B与∠D是对应角
B.边AC与边DF是对应边
C.顶点C与顶点F是对应顶点
D.边BC与边EF是对应边
3.如图,△ABC≌△A'B'C,∠BCB'=30°,则∠ACA'的度数为 ( )
A.20° B.30° C.35° D.40°
4.如图,点F、A、D、C在同一直线上,△ABC≌△DEF,AD=4,CF=10,则AC等于 ( )
A.6 B.7 C.8 D.9
5.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2的度数为 ( )
A.75° B.90°
C.20° D.无法确定
6.如图,已知AC=DB,AO=DO,CD=100 m,则A、B两点间的距离 ( )
A.等于100 m B.大于100 m
C.小于100 m D.无法确定
7.有一条长为24的绳子,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为 ( )
A.3C.48.有下列命题:①有两边和一角对应相等的两个三角形全等;②有两个角和第三个角的平分线对应相等的两个三角形全等;③有两条边和其中一条边上的中线对应相等的两个三角形全等;④有两条边和其中一条边上的高对应相等的两个三角形全等.其中真命题的有 ( )
A.①② B.①④ C.②③ D.③④
二、填空题(每题3分,共18分)
9.能够完全重合的两个图形称为全等图形.全等图形的大小和 都相同.
10.如图,若△ABC≌△DEF,则∠E= 度.
11.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .
12.如图,AC=AB,AE=AD,请写出一个与点D有关的正确结论: .
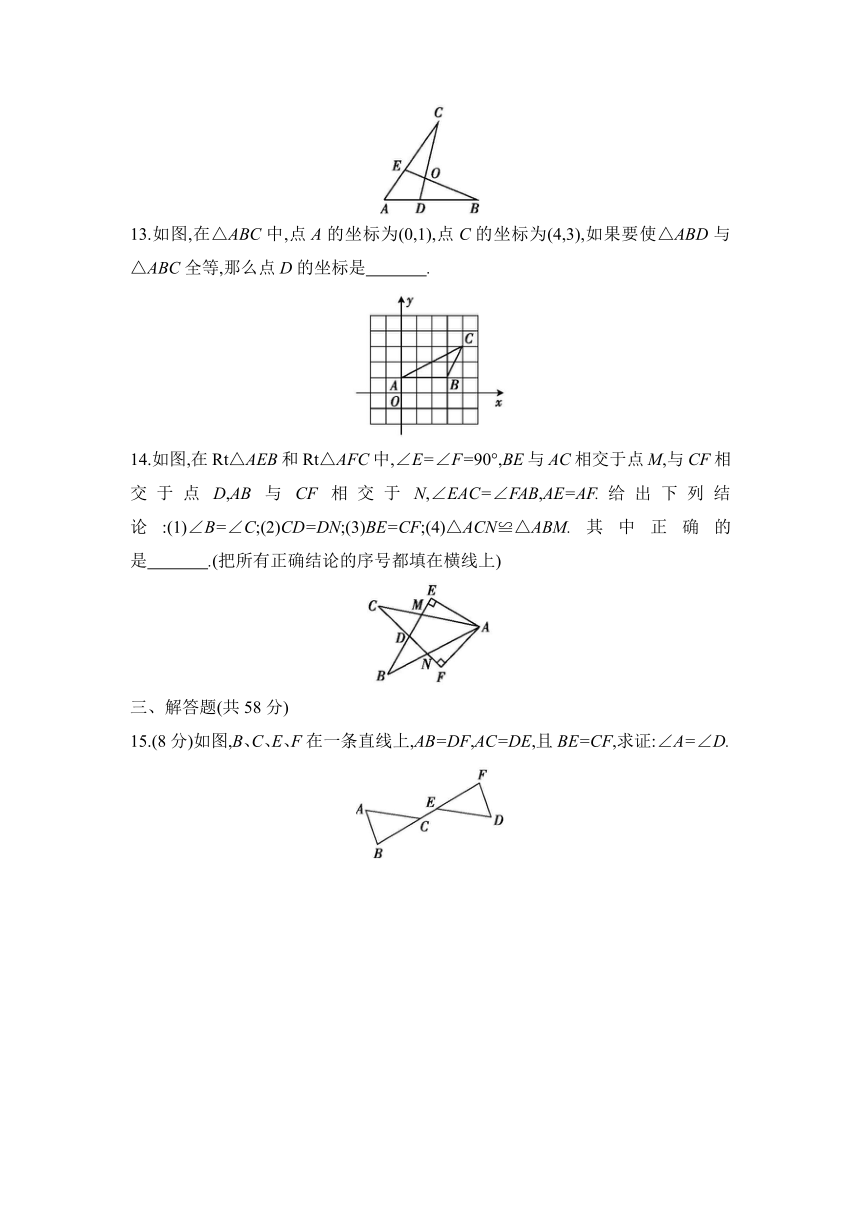
13.如图,在△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 .
14.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠EAC=∠FAB,AE=AF.给出下列结论:(1)∠B=∠C;(2)CD=DN;(3)BE=CF;(4)△ACN≌△ABM.其中正确的是 .(把所有正确结论的序号都填在横线上)
三、解答题(共58分)
15.(8分)如图,B、C、E、F在一条直线上,AB=DF,AC=DE,且BE=CF,求证:∠A=∠D.
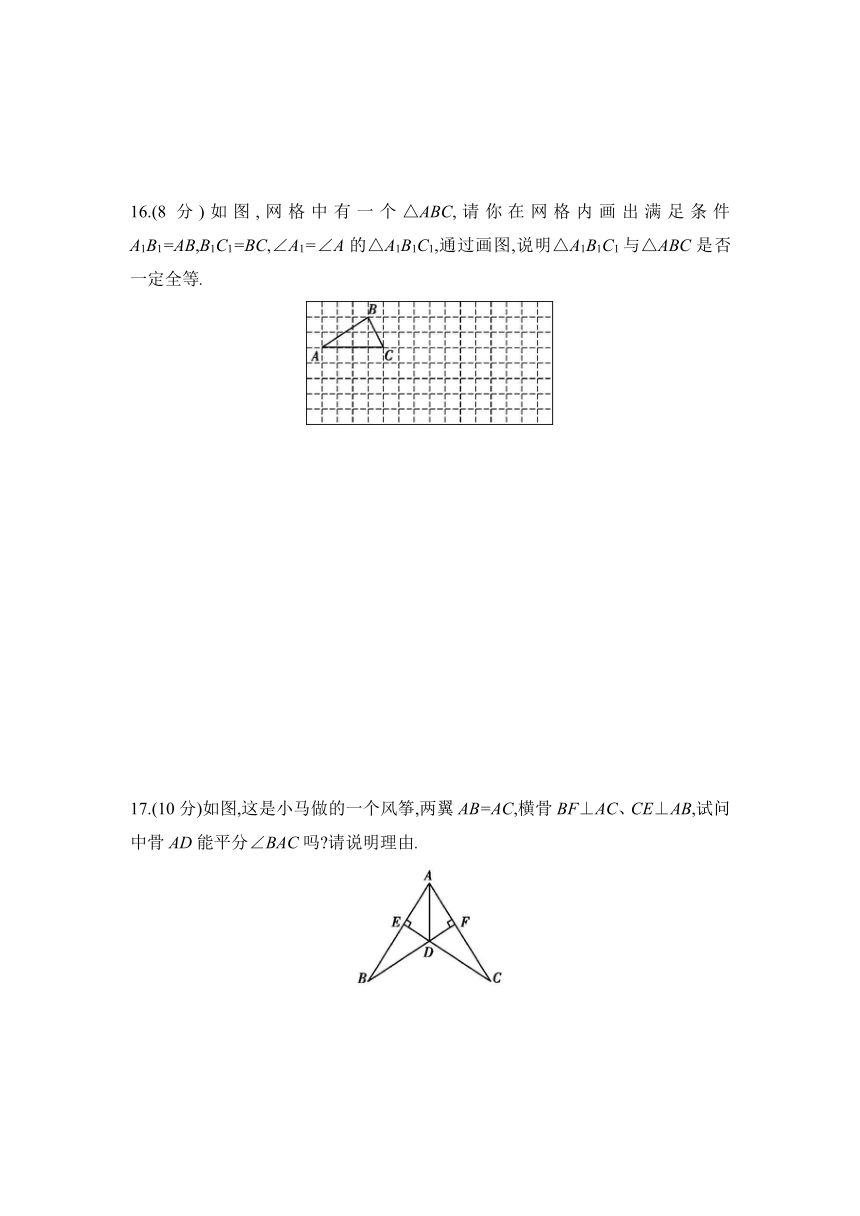
16.(8分)如图,网格中有一个△ABC,请你在网格内画出满足条件A1B1=AB,B1C1=BC,∠A1=∠A的△A1B1C1,通过画图,说明△A1B1C1与△ABC是否一定全等.
17.(10分)如图,这是小马做的一个风筝,两翼AB=AC,横骨BF⊥AC、CE⊥AB,试问中骨AD能平分∠BAC吗 请说明理由.
18.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN,CE⊥MN,垂足分别为D、E,D、A、E三点都在直线MN上,这是教材第14章“A组复习题”第12题,我们证明了DE=BD+CE.若将题中的条件“∠BAC=90°”改为“∠BAC=∠BDA=∠AEC=α,其中α为任意锐角或钝角”,其他条件不变,上述结论DE=BD+CE是否成立 画出图形并说说你的理由.
19.(10分)如图,在△ABC中,AD是BC边上的中线.
(1) 证明:AB+AC >2AD;
(2) 若AB=5,AC=3,试求AD的取值范围.
20.(12分)如图,直线l:y=-x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动,移动了t秒.
(1)求A、B两点的坐标;
(2)当t为何值时,△COM≌△AOB,并求此时M点的坐标.
参考答案
1.B 2.A 3.B 4.B 5.B 6.A 7.D 8.C
9.形状
10.100
11.三角形的稳定性
12.∠ADC=∠AEB或∠CDB=∠CEB(答案不唯一)
13.(4,-1)或(-1,3)或(-1,-1)
14.(1)(3)(4)
15.证明:∵BE=CF,
∴BE-CE=CF-CE,
即BC=FE.
在△ABC和△DFE中,
∴△ABC≌ △DFE(SSS),
∴∠A=∠D.
16.解:△A1B1C1与△ABC不一定全等.
如图,图(1)中△A1B1C1≌△ABC,
图(2)中△A1B 1C1与△ABC不全等.
说明:由于SSA不能判定两个三角形全等,所以必须有一个反例来说明.
17.解:中骨AD能平分∠BAC.
理由如下:
∵BF⊥AC、CE⊥AB,
∴∠AFB=∠AEC=90°,
又∵AB=AC,∠BAF=∠CAE,
∴△BAF≌△CAE(AAS),
∴AF=AE.
在Rt△AED和Rt△AFD中,
AD=AD,AE=AF,
∴Rt△AED≌Rt△AFD(HL),
∴∠EAD=∠FAD,
即中骨AD能平分∠BAC.
18.解: 结论DE=BD+CE成立.
理由:∵∠BDA=∠BAC=α(如图所示的α为钝角),
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠DBA=∠CAE.
又∵∠BDA=∠AEC=α,AB=AC,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
α为锐角时,类似的也可以得到这个结论,图形如下.
19.解:(1)证明:如图,过点C作CE∥AB交AD的延长线于点E.
∵ AD是BC边上的中线,
∴BD=CD.
又∵CE∥AB,
∴∠ABD=∠ECD.
在△ABD与△ECD中,
∴△ABD≌△ECD(ASA),
∴AB=CE,AD=ED,AE=2AD.
在△ACE中,由三边关系定理得AC+CE>AE,
即AB+AC >2AD.
(2)AB=5,AC=3,
在△ACE中,CE-AC即120.解:(1)y=-x+2.
当x=0时,y=2.
当y=0时,-x+2=0,解得x=4,
所以A(4,0),B(0,2).
(2)因为△COM≌△AOB,所以OM=OB=2,
当0当t>4时,OM=t-4=2,所以t=6,
即当t=2或6时,△COM≌△AOB,
此时M点的坐标是(2,0)或(-2,0).
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.下列图形中与已知图形全等的是 ( )
A B C D
2.若△ABC与△DEF全等,A和D,B和E分别是对应点,则下列结论错误的是 ( )
A.∠B与∠D是对应角
B.边AC与边DF是对应边
C.顶点C与顶点F是对应顶点
D.边BC与边EF是对应边
3.如图,△ABC≌△A'B'C,∠BCB'=30°,则∠ACA'的度数为 ( )
A.20° B.30° C.35° D.40°
4.如图,点F、A、D、C在同一直线上,△ABC≌△DEF,AD=4,CF=10,则AC等于 ( )
A.6 B.7 C.8 D.9
5.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2的度数为 ( )
A.75° B.90°
C.20° D.无法确定
6.如图,已知AC=DB,AO=DO,CD=100 m,则A、B两点间的距离 ( )
A.等于100 m B.大于100 m
C.小于100 m D.无法确定
7.有一条长为24的绳子,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为 ( )
A.3
A.①② B.①④ C.②③ D.③④
二、填空题(每题3分,共18分)
9.能够完全重合的两个图形称为全等图形.全等图形的大小和 都相同.
10.如图,若△ABC≌△DEF,则∠E= 度.
11.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .
12.如图,AC=AB,AE=AD,请写出一个与点D有关的正确结论: .
13.如图,在△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 .
14.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠EAC=∠FAB,AE=AF.给出下列结论:(1)∠B=∠C;(2)CD=DN;(3)BE=CF;(4)△ACN≌△ABM.其中正确的是 .(把所有正确结论的序号都填在横线上)
三、解答题(共58分)
15.(8分)如图,B、C、E、F在一条直线上,AB=DF,AC=DE,且BE=CF,求证:∠A=∠D.
16.(8分)如图,网格中有一个△ABC,请你在网格内画出满足条件A1B1=AB,B1C1=BC,∠A1=∠A的△A1B1C1,通过画图,说明△A1B1C1与△ABC是否一定全等.
17.(10分)如图,这是小马做的一个风筝,两翼AB=AC,横骨BF⊥AC、CE⊥AB,试问中骨AD能平分∠BAC吗 请说明理由.
18.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN,CE⊥MN,垂足分别为D、E,D、A、E三点都在直线MN上,这是教材第14章“A组复习题”第12题,我们证明了DE=BD+CE.若将题中的条件“∠BAC=90°”改为“∠BAC=∠BDA=∠AEC=α,其中α为任意锐角或钝角”,其他条件不变,上述结论DE=BD+CE是否成立 画出图形并说说你的理由.
19.(10分)如图,在△ABC中,AD是BC边上的中线.
(1) 证明:AB+AC >2AD;
(2) 若AB=5,AC=3,试求AD的取值范围.
20.(12分)如图,直线l:y=-x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动,移动了t秒.
(1)求A、B两点的坐标;
(2)当t为何值时,△COM≌△AOB,并求此时M点的坐标.
参考答案
1.B 2.A 3.B 4.B 5.B 6.A 7.D 8.C
9.形状
10.100
11.三角形的稳定性
12.∠ADC=∠AEB或∠CDB=∠CEB(答案不唯一)
13.(4,-1)或(-1,3)或(-1,-1)
14.(1)(3)(4)
15.证明:∵BE=CF,
∴BE-CE=CF-CE,
即BC=FE.
在△ABC和△DFE中,
∴△ABC≌ △DFE(SSS),
∴∠A=∠D.
16.解:△A1B1C1与△ABC不一定全等.
如图,图(1)中△A1B1C1≌△ABC,
图(2)中△A1B 1C1与△ABC不全等.
说明:由于SSA不能判定两个三角形全等,所以必须有一个反例来说明.
17.解:中骨AD能平分∠BAC.
理由如下:
∵BF⊥AC、CE⊥AB,
∴∠AFB=∠AEC=90°,
又∵AB=AC,∠BAF=∠CAE,
∴△BAF≌△CAE(AAS),
∴AF=AE.
在Rt△AED和Rt△AFD中,
AD=AD,AE=AF,
∴Rt△AED≌Rt△AFD(HL),
∴∠EAD=∠FAD,
即中骨AD能平分∠BAC.
18.解: 结论DE=BD+CE成立.
理由:∵∠BDA=∠BAC=α(如图所示的α为钝角),
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠DBA=∠CAE.
又∵∠BDA=∠AEC=α,AB=AC,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
α为锐角时,类似的也可以得到这个结论,图形如下.
19.解:(1)证明:如图,过点C作CE∥AB交AD的延长线于点E.
∵ AD是BC边上的中线,
∴BD=CD.
又∵CE∥AB,
∴∠ABD=∠ECD.
在△ABD与△ECD中,
∴△ABD≌△ECD(ASA),
∴AB=CE,AD=ED,AE=2AD.
在△ACE中,由三边关系定理得AC+CE>AE,
即AB+AC >2AD.
(2)AB=5,AC=3,
在△ACE中,CE-AC
当x=0时,y=2.
当y=0时,-x+2=0,解得x=4,
所以A(4,0),B(0,2).
(2)因为△COM≌△AOB,所以OM=OB=2,
当0
即当t=2或6时,△COM≌△AOB,
此时M点的坐标是(2,0)或(-2,0).
