【课时作业】第14章 全等三角形 复习课作业设计(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第14章 全等三角形 复习课作业设计(含答案)2024-2025学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 71.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览

文档简介
第14章 全等三角形 复习课作业设计
一、作业目标
1.了解全等图形的概念和性质,能够找准全等图形的对应元素.
2.掌握全等三角形的判断方法,能够利用三角形全等证明线段和角相等.
3.能够利用三角形全等解决实际问题.
二、作业内容
【基础达标】
1下列说法中正确的是 ( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
2如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B= ( )
A.60° B.100° C.120° D.135°
3如图,若△ABC≌△ADE,则下列结论中不一定成立的是 ( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠C=∠E
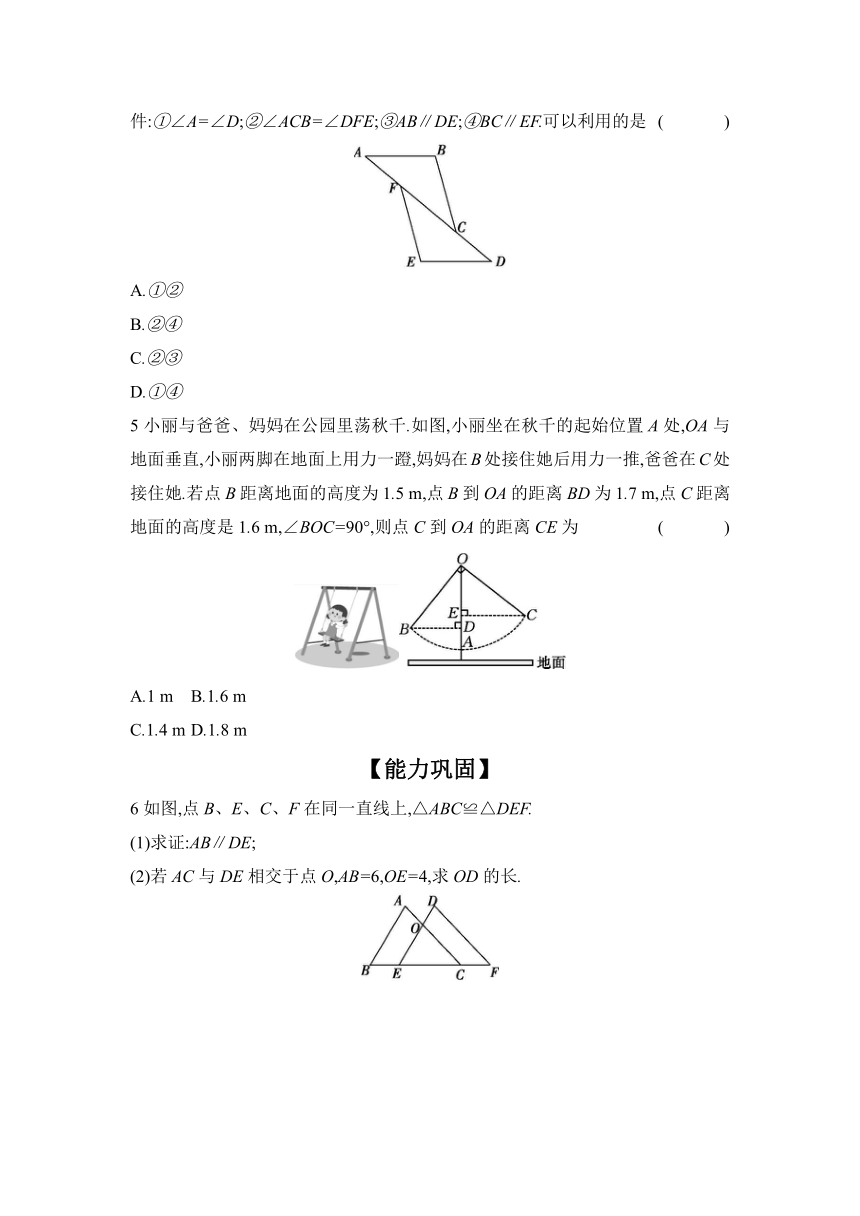
4如图,已知BC=EF,AF=DC,A、F、C、D四点在同一直线上.要利用“SAS”来判定△ABC≌△DEF,下列四个条件:①∠A=∠D;②∠ACB=∠DFE;③AB∥DE;④BC∥EF.可以利用的是 ( )
A.①②
B.②④
C.②③
D.①④
5小丽与爸爸、妈妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在C处接住她.若点B距离地面的高度为1.5 m,点B到OA的距离BD为1.7 m,点C距离地面的高度是1.6 m,∠BOC=90°,则点C到OA的距离CE为 ( )
A.1 m B.1.6 m
C.1.4 m D.1.8 m
【能力巩固】
6如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
7如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.求证:
(1)△AMB≌△CNA;
(2)∠BAC=90°.
【素养拓展】
8如图,AB=14,AC=6,AC⊥AB,BD⊥AB,垂足分别为A、B.点P从点A出发,以每秒2个单位长度的速度沿AB向点B运动;点Q从点B出发,以每秒a个单位长度的速度沿射线BD方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与△CAP全等时,求a的值.
参考答案
1.C 2.C 3.A 4.B 5.D
6.解:(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB//DE.
(2)∵△ABC≌△DEF,
∴AB=DE=6.
∵OE=4,
∴OD=DE-OE=6-4=2.
7.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
∴Rt△AMB≌Rt△CNA(HL).
(2)由(1)得Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN.
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°-90°=90°.
8.解:当△CAP≌△PBQ时,AC=PB,AP=BQ.
∵AC=6,AB=14,
∴PB=6,AP=AB-PB=14-6=8,
∴BQ=8,∴8÷a=8÷2,解得a=2;
当△CAP≌△QBP时,AC=BQ,AP=BP.
∵AC=6,AB=14,∴BQ=6,AP=BP=7,
∴6÷a=7÷2,解得a=.
∴a的值是2或.
一、作业目标
1.了解全等图形的概念和性质,能够找准全等图形的对应元素.
2.掌握全等三角形的判断方法,能够利用三角形全等证明线段和角相等.
3.能够利用三角形全等解决实际问题.
二、作业内容
【基础达标】
1下列说法中正确的是 ( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
2如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B= ( )
A.60° B.100° C.120° D.135°
3如图,若△ABC≌△ADE,则下列结论中不一定成立的是 ( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠C=∠E
4如图,已知BC=EF,AF=DC,A、F、C、D四点在同一直线上.要利用“SAS”来判定△ABC≌△DEF,下列四个条件:①∠A=∠D;②∠ACB=∠DFE;③AB∥DE;④BC∥EF.可以利用的是 ( )
A.①②
B.②④
C.②③
D.①④
5小丽与爸爸、妈妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在C处接住她.若点B距离地面的高度为1.5 m,点B到OA的距离BD为1.7 m,点C距离地面的高度是1.6 m,∠BOC=90°,则点C到OA的距离CE为 ( )
A.1 m B.1.6 m
C.1.4 m D.1.8 m
【能力巩固】
6如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
7如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.求证:
(1)△AMB≌△CNA;
(2)∠BAC=90°.
【素养拓展】
8如图,AB=14,AC=6,AC⊥AB,BD⊥AB,垂足分别为A、B.点P从点A出发,以每秒2个单位长度的速度沿AB向点B运动;点Q从点B出发,以每秒a个单位长度的速度沿射线BD方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与△CAP全等时,求a的值.
参考答案
1.C 2.C 3.A 4.B 5.D
6.解:(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB//DE.
(2)∵△ABC≌△DEF,
∴AB=DE=6.
∵OE=4,
∴OD=DE-OE=6-4=2.
7.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
∴Rt△AMB≌Rt△CNA(HL).
(2)由(1)得Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN.
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°-90°=90°.
8.解:当△CAP≌△PBQ时,AC=PB,AP=BQ.
∵AC=6,AB=14,
∴PB=6,AP=AB-PB=14-6=8,
∴BQ=8,∴8÷a=8÷2,解得a=2;
当△CAP≌△QBP时,AC=BQ,AP=BP.
∵AC=6,AB=14,∴BQ=6,AP=BP=7,
∴6÷a=7÷2,解得a=.
∴a的值是2或.
