【课时作业】第15章 轴对称图形与等腰三角形 测试卷(含答案)2024-2025学年数学沪科版八年级上册
文档属性
| 名称 | 【课时作业】第15章 轴对称图形与等腰三角形 测试卷(含答案)2024-2025学年数学沪科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览


文档简介
第15章 轴对称图形与等腰三角形 测试卷
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.下列图案中,是轴对称图形的是 ( )
A B C D
2.在平面直角坐标系中,点P(-3,2)关于y轴对称点的坐标是 ( )
A.(-3,-2) B.(3,2)
C.(2,-3) D.(3,-2)
3.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为 ( )
A.8或10 B.8
C.10 D.6或12
4.如图,在直角△ABC中,∠BAC=90°,BC=10,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为 ( )
A.16 B.15 C.14 D.12
5.等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形的一个底角的度数是 ( )
A.45° B.22.5°或67.5°
C.45°或135° D.45°或67.5°
6.如图,在△ABC中,AB=AC,EB=EC,那么图中的全等三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
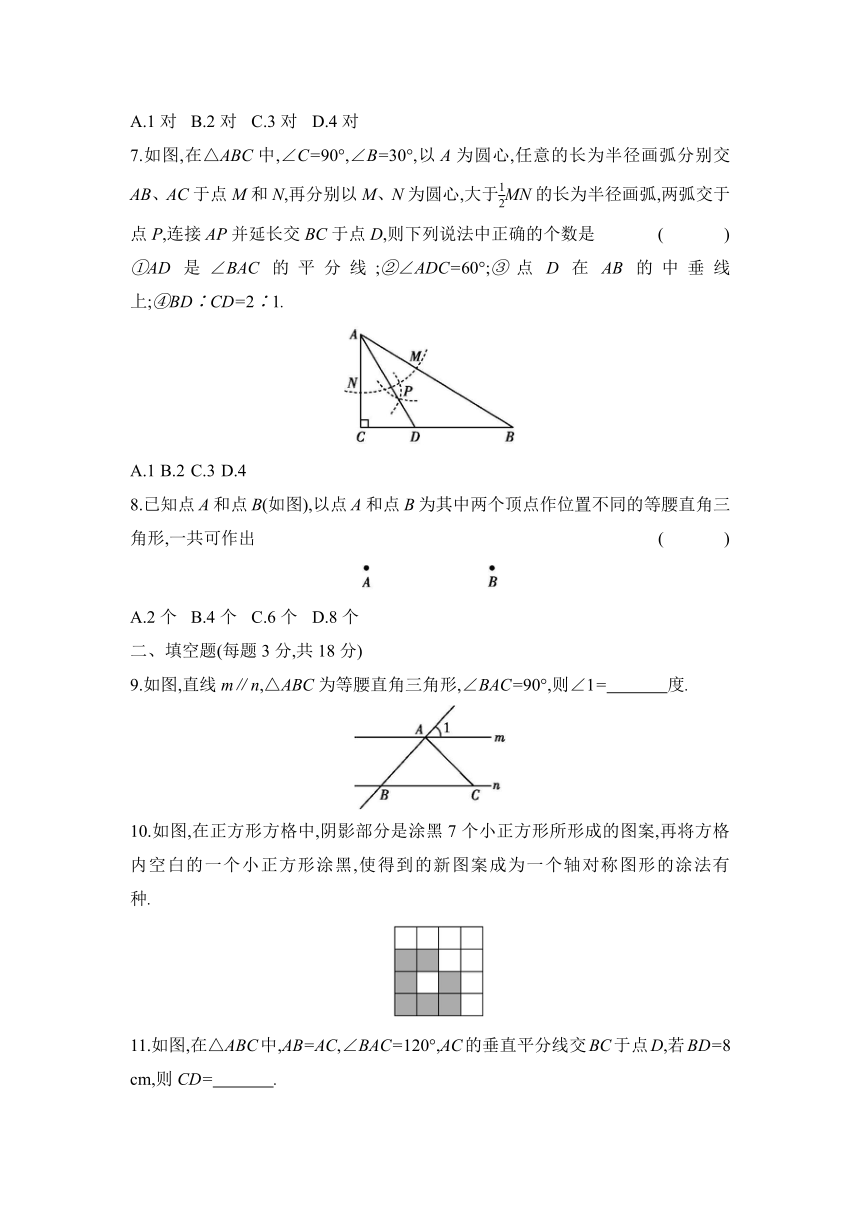
7.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意的长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是 ( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④BD∶CD=2∶1.
A.1 B.2 C.3 D.4
8.已知点A和点B(如图),以点A和点B为其中两个顶点作位置不同的等腰直角三角形,一共可作出 ( )
A.2个 B.4个 C.6个 D.8个
二、填空题(每题3分,共18分)
9.如图,直线m∥n,△ABC为等腰直角三角形,∠BAC=90°,则∠1= 度.
10.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 种.
11.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,若BD=8 cm,则CD= .
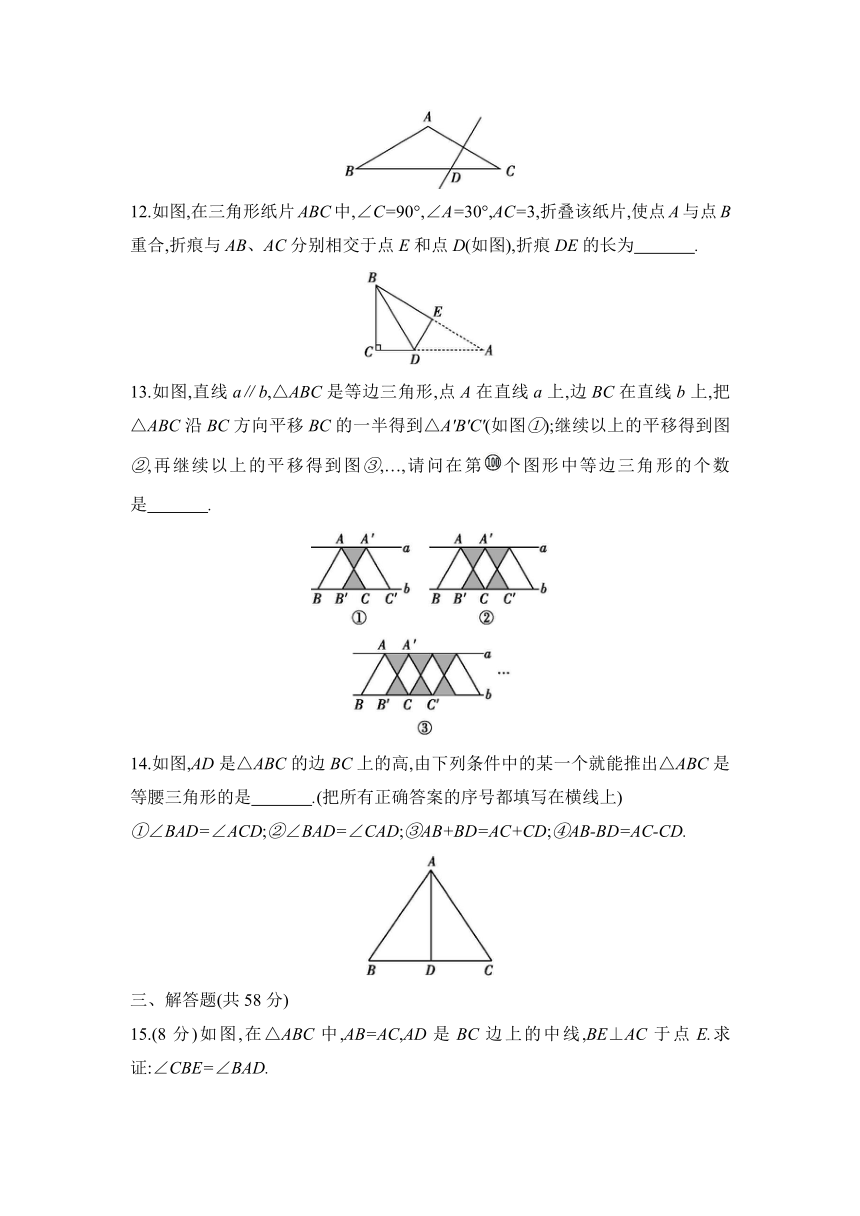
12.如图,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点E和点D(如图),折痕DE的长为 .
13.如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A'B'C'(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…,请问在第个图形中等边三角形的个数是 .
14.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是 .(把所有正确答案的序号都填写在横线上)
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB-BD=AC-CD.
三、解答题(共58分)
15.(8分)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
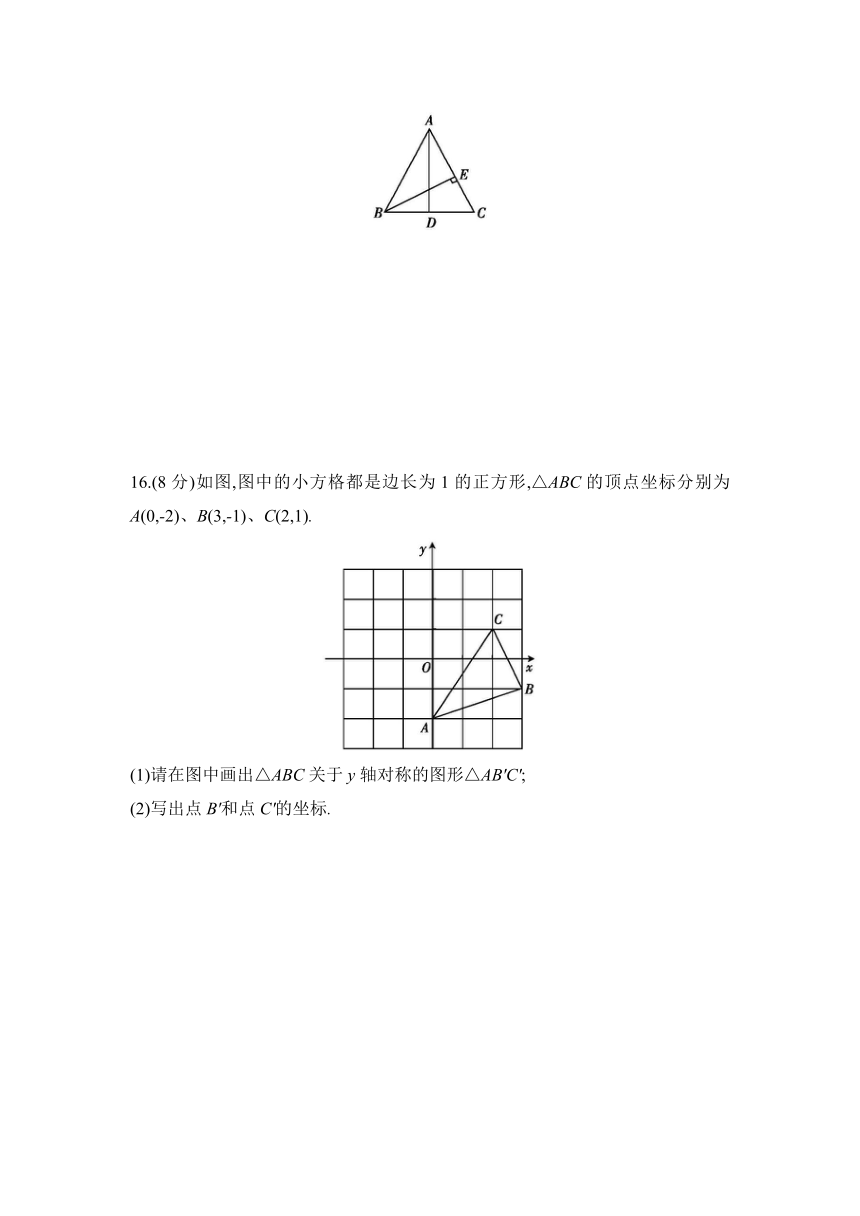
16.(8分)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为A(0,-2)、B(3,-1)、C(2,1).
(1)请在图中画出△ABC关于y轴对称的图形△AB'C';
(2)写出点B'和点C'的坐标.
17.(10分)如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
18.(10分)如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC、AD相交于点E.
(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长.
19.(10分)如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.求证:
(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
20.(12分)在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并说明.
图1 图2
参考答案
1.D 2.B 3.C 4.A 5.B 6.C 7.D 8.C
9.45
10.3
11.4 cm
12.1
13.400
14.②③④
15.证明:(方法1)∵AB=AC,
∴△ABC是等腰三角形.
∵AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠CAD+∠C=90°.
∵BE⊥AC,∴∠CBE+∠C=90°,∴∠CBE=∠CAD,
∴∠CBE=∠BAD.
(方法2)∵AB=AC,∴∠ABC=∠C,
又∵AD是BC边上的中线,∴AD⊥BC,
∴∠BAD+∠ABC=90°.
∵BE⊥AC,∴∠CBE+∠C=90°,
∴∠CBE=∠BAD.
16.解:(1)略;
(2)B'(-3,-1)和C'(-2,1).
17.解:(1)∵AB=AC,∴∠B=∠C=30°.
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°-30°-30°=120°.
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°.
(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.
18.解:(1)证明:在Rt△ACE和Rt△BDE中,
∵∠AEC与∠BED是对顶角,
∴∠AEC=∠BED.
∵∠C=∠D=90°,AC=BD,
∴Rt△ACE≌Rt△BDE,∴AE=BE.
(2)∵∠AEC=45°,∠C=90°,
∴∠CAE=45°,∴CE=AC=1.
19.证明:(1)因为∠1=∠2,OD⊥AB,OE⊥AC,
所以OE=OD(角平分线上的点到这个角的两边的距离相等),∠ODB=∠OEC.
在△BOD和△COE中,
所以△BOD≌△COE(ASA),
所以OB=OC(全等三角形的对应边相等).
(2)在△BOD和△COE中,
所以△BOD≌△COE(AAS),所以OD=OE(全等三角形的对应边相等).因为OD⊥AB,OE⊥AC,所以AO平分∠BAC(到一个角的两边距离相等的点在这个角的平分线上),所以∠1=∠2.
20.解:(1)证明:∵D是AB中点,
AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,
又∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
∴△AEC≌△CGB,∴AE=CG.
(2)BE=CM.
理由:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,∴BE=CM.
(时间:60分钟 总分:100分)
一、选择题(每题3分,共24分)
1.下列图案中,是轴对称图形的是 ( )
A B C D
2.在平面直角坐标系中,点P(-3,2)关于y轴对称点的坐标是 ( )
A.(-3,-2) B.(3,2)
C.(2,-3) D.(3,-2)
3.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为 ( )
A.8或10 B.8
C.10 D.6或12
4.如图,在直角△ABC中,∠BAC=90°,BC=10,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为 ( )
A.16 B.15 C.14 D.12
5.等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形的一个底角的度数是 ( )
A.45° B.22.5°或67.5°
C.45°或135° D.45°或67.5°
6.如图,在△ABC中,AB=AC,EB=EC,那么图中的全等三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
7.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意的长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是 ( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④BD∶CD=2∶1.
A.1 B.2 C.3 D.4
8.已知点A和点B(如图),以点A和点B为其中两个顶点作位置不同的等腰直角三角形,一共可作出 ( )
A.2个 B.4个 C.6个 D.8个
二、填空题(每题3分,共18分)
9.如图,直线m∥n,△ABC为等腰直角三角形,∠BAC=90°,则∠1= 度.
10.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 种.
11.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,若BD=8 cm,则CD= .
12.如图,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点E和点D(如图),折痕DE的长为 .
13.如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A'B'C'(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…,请问在第个图形中等边三角形的个数是 .
14.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是 .(把所有正确答案的序号都填写在横线上)
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB-BD=AC-CD.
三、解答题(共58分)
15.(8分)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
16.(8分)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为A(0,-2)、B(3,-1)、C(2,1).
(1)请在图中画出△ABC关于y轴对称的图形△AB'C';
(2)写出点B'和点C'的坐标.
17.(10分)如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
18.(10分)如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC、AD相交于点E.
(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长.
19.(10分)如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.求证:
(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
20.(12分)在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并说明.
图1 图2
参考答案
1.D 2.B 3.C 4.A 5.B 6.C 7.D 8.C
9.45
10.3
11.4 cm
12.1
13.400
14.②③④
15.证明:(方法1)∵AB=AC,
∴△ABC是等腰三角形.
∵AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠CAD+∠C=90°.
∵BE⊥AC,∴∠CBE+∠C=90°,∴∠CBE=∠CAD,
∴∠CBE=∠BAD.
(方法2)∵AB=AC,∴∠ABC=∠C,
又∵AD是BC边上的中线,∴AD⊥BC,
∴∠BAD+∠ABC=90°.
∵BE⊥AC,∴∠CBE+∠C=90°,
∴∠CBE=∠BAD.
16.解:(1)略;
(2)B'(-3,-1)和C'(-2,1).
17.解:(1)∵AB=AC,∴∠B=∠C=30°.
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°-30°-30°=120°.
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°.
(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.
18.解:(1)证明:在Rt△ACE和Rt△BDE中,
∵∠AEC与∠BED是对顶角,
∴∠AEC=∠BED.
∵∠C=∠D=90°,AC=BD,
∴Rt△ACE≌Rt△BDE,∴AE=BE.
(2)∵∠AEC=45°,∠C=90°,
∴∠CAE=45°,∴CE=AC=1.
19.证明:(1)因为∠1=∠2,OD⊥AB,OE⊥AC,
所以OE=OD(角平分线上的点到这个角的两边的距离相等),∠ODB=∠OEC.
在△BOD和△COE中,
所以△BOD≌△COE(ASA),
所以OB=OC(全等三角形的对应边相等).
(2)在△BOD和△COE中,
所以△BOD≌△COE(AAS),所以OD=OE(全等三角形的对应边相等).因为OD⊥AB,OE⊥AC,所以AO平分∠BAC(到一个角的两边距离相等的点在这个角的平分线上),所以∠1=∠2.
20.解:(1)证明:∵D是AB中点,
AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,
又∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
∴△AEC≌△CGB,∴AE=CG.
(2)BE=CM.
理由:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,∴BE=CM.
