【课时作业】第2章 三角形 复习课(含答案)2024-2025学年数学湘教版八年级上册
文档属性
| 名称 | 【课时作业】第2章 三角形 复习课(含答案)2024-2025学年数学湘教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-10 00:00:00 | ||
图片预览




文档简介
第2章 复习课
【基础达标】
1下列命题中是真命题的是 ( )
A.两个锐角之和为钝角
B.两个锐角之和为锐角
C.钝角大于它的补角
D.锐角小于它的余角
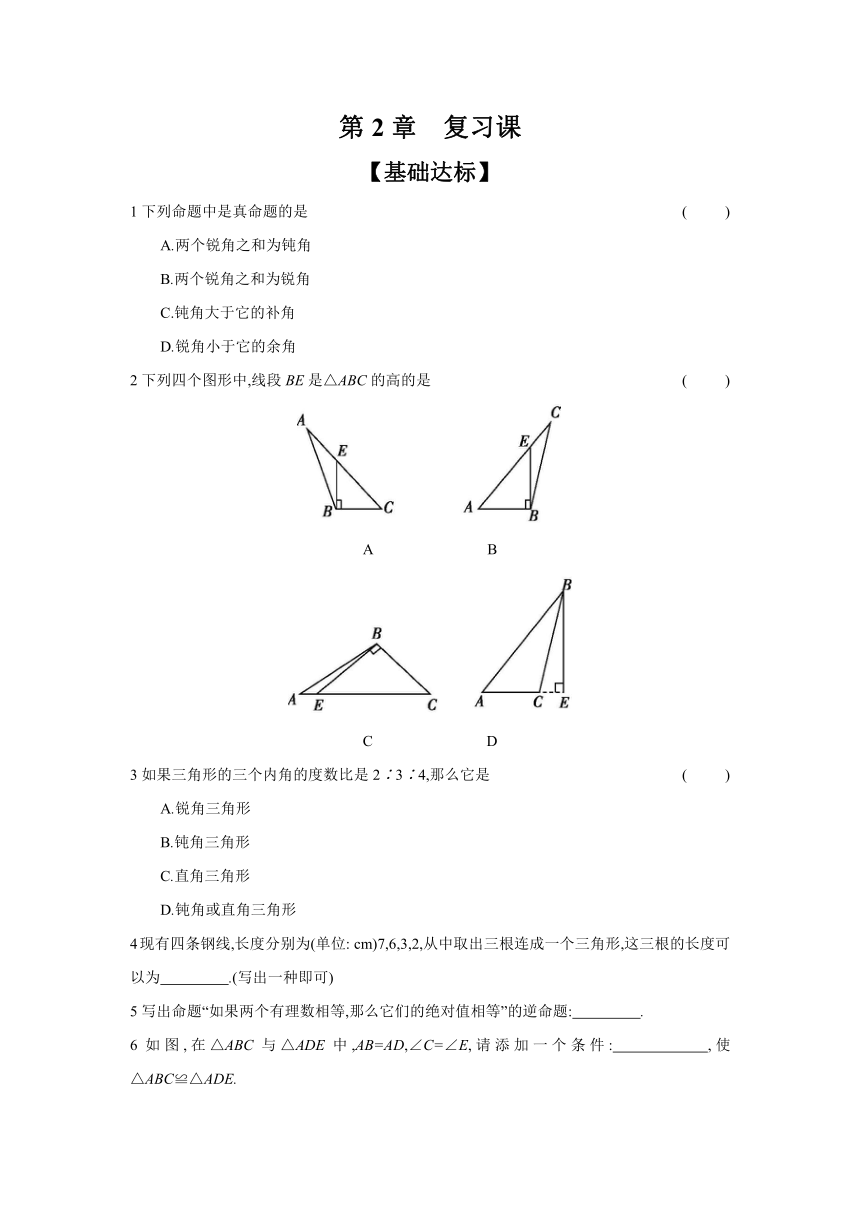
2下列四个图形中,线段BE是△ABC的高的是 ( )
A B
C D
3如果三角形的三个内角的度数比是2∶3∶4,那么它是 ( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角或直角三角形
4现有四条钢线,长度分别为(单位: cm)7,6,3,2,从中取出三根连成一个三角形,这三根的长度可以为 .(写出一种即可)
5写出命题“如果两个有理数相等,那么它们的绝对值相等”的逆命题: .
6如图,在△ABC与△ADE中,AB=AD,∠C=∠E,请添加一个条件: ,使△ABC≌△ADE.
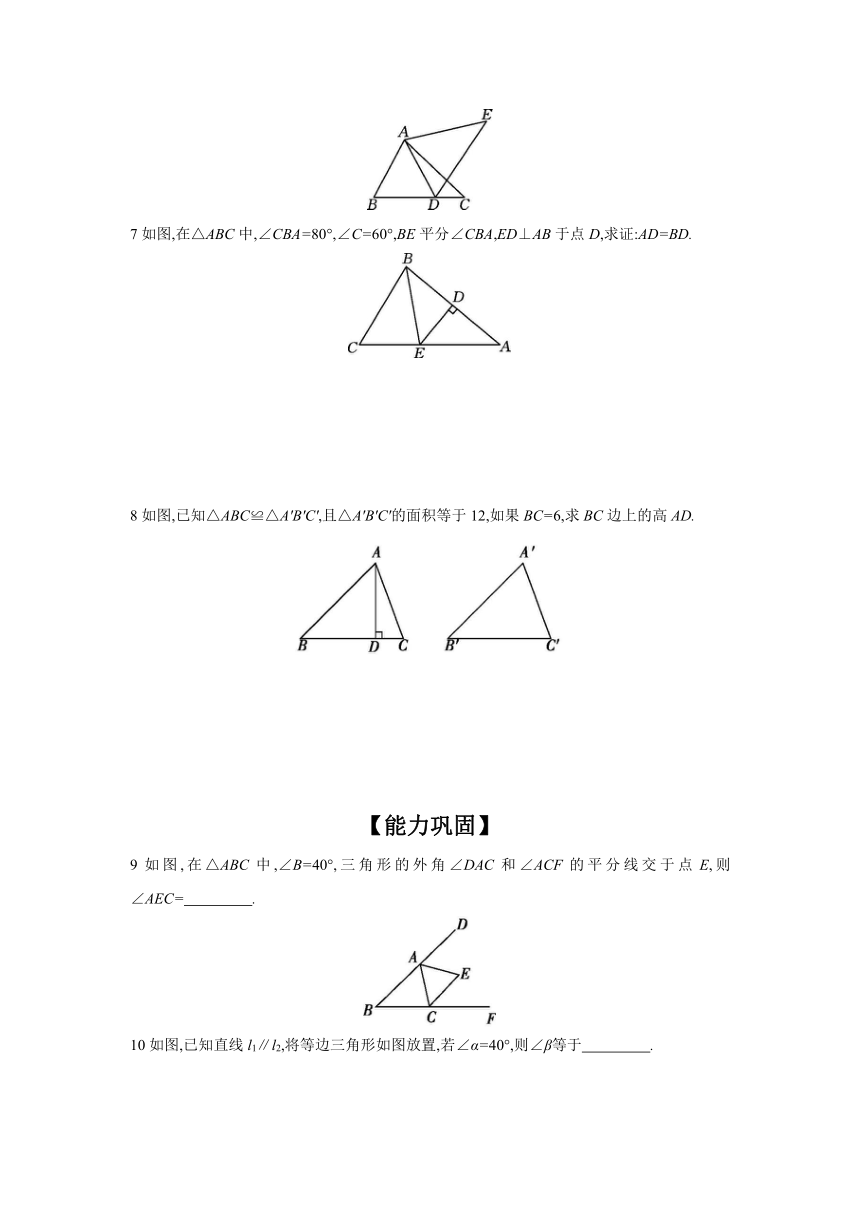
7如图,在△ABC中,∠CBA=80°,∠C=60°,BE平分∠CBA,ED⊥AB于点D,求证:AD=BD.
8如图,已知△ABC≌△A'B'C',且△A'B'C'的面积等于12,如果BC=6,求BC边上的高AD.
【能力巩固】
9如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
10如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于 .
11如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E.
求证:DE=EC.
12阅读下题及证明过程.
已知:如图,AB=AC,∠ABP=∠ACP,求证:∠BAP=∠CAP.
证明:∵AB=AC,∠ABP=∠ACP,PA=PA,
∴△PAB≌△PAC(第一步),
∴∠BAP=∠CAP(第二步).
上面的证明过程是否正确 若正确,请写出每一步的推理依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
13如图,在△ABC中,AD⊥BC于点D,E为线段AB上一点,连接CE交AD于点F,已知BD=DF,AD=CD.
(1)求证:CF=AB.
(2)若CF=2BE,求∠BCE的度数.
【素养拓展】
14如图,在等边△ABC中,其边长为1,D是BC的中点,点E,F分别在AB,AC边上,且∠EDF=120°.
(1)写出DE与DF的数量关系,并证明.
(2)若BE,DE,CF能围成一个三角形,求出这个三角形最大内角的度数.(要求:写出思路,画出图形,直接给出结果即可)
15阅读理解
倍长中线是初中数学一种重要的数学思想,如图1,在△ABC中,AD是BC边上的中线,若延长AD至点E,使DE=AD,连接CE,可根据“SAS”证明△ABD≌△ECD,则AB=EC.
问题提出
(1)如图2,在△DEF中,DE=3,DF=7,G是EF的中点,求中线DG的取值范围.
问题探究
(2)如图3,在四边形ABCD中,AB∥CD,E是BC的中点.若AE是∠BAD的平分线,则AB,AD,CD之间的等量关系是 .
问题解决
(3)如图4,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点.若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
参考答案
基础达标作业
1.C 2.D 3.A
4.答案不唯一,如7,6,3.(写出一种即可)
5.如果两个有理数的绝对值相等,那么这两个有理数相等
6.∠BAC=∠DAE(答案不唯一)
7.证明:∵∠CBA=80°,∠C=60°,
∴∠A=180°-80°-60°=40°.
∵BE平分∠CBA,
∴∠EBA=∠CBA=40°,
∴∠EBA=∠A,
∴BE=EA.
∵ED⊥AB,
∴AD=BD.
8.解:∵△ABC≌△A'B'C',∴S△ABC=S△A'B'C',
∵△A'B'C'的面积等于12,
∴△ABC的面积等于12.
∵S△ABC=BC·AD,∴AD=12×2÷6=4.
故BC边上的高AD为4.
能力巩固作业
9.70°
10.20°
11.证明:如图,连接BE.
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
∵DE⊥AB,∠C=90°,
∴∠BDE=∠C.
∵∠ABE=∠CBE,BE=BE,
∴△BDE≌△BCE(AAS),
∴DE=CE.
12.解:上面的过程不正确.
错在第一步.
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠ABP=∠ACP,
∴∠ABC+∠ABP=∠ACB+∠ACP,即∠PBC=∠PCB,
∴PB=PC.
在△PAB和△PAC中,
∴△PAB≌△PAC(SAS),
∴∠BAP=∠CAP.
13.解:(1)证明:∵AD⊥BC于点D,
∴∠ADB=∠CDF=90°.
∵BD=DF,AD=CD,
∴△ABD≌△CFD(SAS),
∴CF=AB.
(2)∵∠ADC=90°,AD=CD,
∴∠ACD=∠CAD=45°.
∵△ABD≌△CFD,
∴∠BAD=∠ECB.
∵∠AFE=∠CFD,
∴∠AEC=∠ADC=90°.
∵AB=CF=2AE,
∴CE垂直平分AB,
∴CE平分∠ACB,
∴∠BCE=∠ACB=22.5°.
素养拓展作业
14.
图1
解:(1)结论:DE=DF.
证明:如图1,连接AD,作DN⊥AB,DM⊥AC,垂足分别为N、M.
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵BD=DC,
∴∠BAD=∠CAD,
∴DN=DM.
∵∠EDF=120°,
∴∠EDF+∠BAC=180°,∠AED+AFD=180°.
∵∠AED+∠DEN=180°,
∴∠DFM=∠DEN.
在△DNE和△DMF中,
∴△DNE≌△DMF,
∴DE=DF.
(2)最大内角为120°.
图2
证明:如图2中,延长FD到M使得DF=DM,连接BM,EM.
在△DFC和△DMB中,
∴△DFC≌△DMB,
∴∠C=∠MBD=60°,BM=CF,
∵DE=DF=DM,∠EDM=180°-∠EDF=60°,
∴△EDM是等边三角形,
∴EM=DE,
∴EB、ED、CF能围成△EBM,
最大内角∠EBM=∠EBC+∠DBM=60°+60°=120°.
15.解:(1)如图1,延长DG至点H,使GH=DG,连接FH.
∵G是EF的中点,∴EG=FG,
在△DGE和△HGF中,,
∴△DGE≌△HGF(SAS),∴FH=DE=3.
在△DFH中,DF-FH∴7-3∵DH=2DG,∴4<2DG<10,∴2(2)AD=AB+DC.
提示:如图2,延长AE,DC交于点F.
∵AB∥CD,∴∠CFE=∠EAB.
∵E是BC的中点∴CE=EB.
∵∠CEF=∠AEB,
∴△CEF≌△BEA(AAS),∴AB=CF.
∵AF平分∠DAB,∴∠DAF=∠EAB.
∵∠EAB=∠CFE,∴∠DAF=∠DFA,
∴AD=DF.
∵DF=DC+CF=DC+AB,
∴AD=AB+DC.
(3)AB=AF+CF.
证明:如图3,延长AE交DC的延长线于点G.
∵AB∥DG,∴∠G=∠EAB.
∵CE=EB,∠CEG=∠BEA,
∴△CEG≌△BEA(AAS),∴AB=CG.
∵AE平分∠FAB,∴∠FAG=∠EAB.
∵∠G=∠EAB,∴∠FAG=∠G,∴AF=FG.
∵CG=CF+FG=CF+AF,∴AB=AF+CF.
【基础达标】
1下列命题中是真命题的是 ( )
A.两个锐角之和为钝角
B.两个锐角之和为锐角
C.钝角大于它的补角
D.锐角小于它的余角
2下列四个图形中,线段BE是△ABC的高的是 ( )
A B
C D
3如果三角形的三个内角的度数比是2∶3∶4,那么它是 ( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角或直角三角形
4现有四条钢线,长度分别为(单位: cm)7,6,3,2,从中取出三根连成一个三角形,这三根的长度可以为 .(写出一种即可)
5写出命题“如果两个有理数相等,那么它们的绝对值相等”的逆命题: .
6如图,在△ABC与△ADE中,AB=AD,∠C=∠E,请添加一个条件: ,使△ABC≌△ADE.
7如图,在△ABC中,∠CBA=80°,∠C=60°,BE平分∠CBA,ED⊥AB于点D,求证:AD=BD.
8如图,已知△ABC≌△A'B'C',且△A'B'C'的面积等于12,如果BC=6,求BC边上的高AD.
【能力巩固】
9如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
10如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于 .
11如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E.
求证:DE=EC.
12阅读下题及证明过程.
已知:如图,AB=AC,∠ABP=∠ACP,求证:∠BAP=∠CAP.
证明:∵AB=AC,∠ABP=∠ACP,PA=PA,
∴△PAB≌△PAC(第一步),
∴∠BAP=∠CAP(第二步).
上面的证明过程是否正确 若正确,请写出每一步的推理依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
13如图,在△ABC中,AD⊥BC于点D,E为线段AB上一点,连接CE交AD于点F,已知BD=DF,AD=CD.
(1)求证:CF=AB.
(2)若CF=2BE,求∠BCE的度数.
【素养拓展】
14如图,在等边△ABC中,其边长为1,D是BC的中点,点E,F分别在AB,AC边上,且∠EDF=120°.
(1)写出DE与DF的数量关系,并证明.
(2)若BE,DE,CF能围成一个三角形,求出这个三角形最大内角的度数.(要求:写出思路,画出图形,直接给出结果即可)
15阅读理解
倍长中线是初中数学一种重要的数学思想,如图1,在△ABC中,AD是BC边上的中线,若延长AD至点E,使DE=AD,连接CE,可根据“SAS”证明△ABD≌△ECD,则AB=EC.
问题提出
(1)如图2,在△DEF中,DE=3,DF=7,G是EF的中点,求中线DG的取值范围.
问题探究
(2)如图3,在四边形ABCD中,AB∥CD,E是BC的中点.若AE是∠BAD的平分线,则AB,AD,CD之间的等量关系是 .
问题解决
(3)如图4,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点.若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
参考答案
基础达标作业
1.C 2.D 3.A
4.答案不唯一,如7,6,3.(写出一种即可)
5.如果两个有理数的绝对值相等,那么这两个有理数相等
6.∠BAC=∠DAE(答案不唯一)
7.证明:∵∠CBA=80°,∠C=60°,
∴∠A=180°-80°-60°=40°.
∵BE平分∠CBA,
∴∠EBA=∠CBA=40°,
∴∠EBA=∠A,
∴BE=EA.
∵ED⊥AB,
∴AD=BD.
8.解:∵△ABC≌△A'B'C',∴S△ABC=S△A'B'C',
∵△A'B'C'的面积等于12,
∴△ABC的面积等于12.
∵S△ABC=BC·AD,∴AD=12×2÷6=4.
故BC边上的高AD为4.
能力巩固作业
9.70°
10.20°
11.证明:如图,连接BE.
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
∵DE⊥AB,∠C=90°,
∴∠BDE=∠C.
∵∠ABE=∠CBE,BE=BE,
∴△BDE≌△BCE(AAS),
∴DE=CE.
12.解:上面的过程不正确.
错在第一步.
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠ABP=∠ACP,
∴∠ABC+∠ABP=∠ACB+∠ACP,即∠PBC=∠PCB,
∴PB=PC.
在△PAB和△PAC中,
∴△PAB≌△PAC(SAS),
∴∠BAP=∠CAP.
13.解:(1)证明:∵AD⊥BC于点D,
∴∠ADB=∠CDF=90°.
∵BD=DF,AD=CD,
∴△ABD≌△CFD(SAS),
∴CF=AB.
(2)∵∠ADC=90°,AD=CD,
∴∠ACD=∠CAD=45°.
∵△ABD≌△CFD,
∴∠BAD=∠ECB.
∵∠AFE=∠CFD,
∴∠AEC=∠ADC=90°.
∵AB=CF=2AE,
∴CE垂直平分AB,
∴CE平分∠ACB,
∴∠BCE=∠ACB=22.5°.
素养拓展作业
14.
图1
解:(1)结论:DE=DF.
证明:如图1,连接AD,作DN⊥AB,DM⊥AC,垂足分别为N、M.
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵BD=DC,
∴∠BAD=∠CAD,
∴DN=DM.
∵∠EDF=120°,
∴∠EDF+∠BAC=180°,∠AED+AFD=180°.
∵∠AED+∠DEN=180°,
∴∠DFM=∠DEN.
在△DNE和△DMF中,
∴△DNE≌△DMF,
∴DE=DF.
(2)最大内角为120°.
图2
证明:如图2中,延长FD到M使得DF=DM,连接BM,EM.
在△DFC和△DMB中,
∴△DFC≌△DMB,
∴∠C=∠MBD=60°,BM=CF,
∵DE=DF=DM,∠EDM=180°-∠EDF=60°,
∴△EDM是等边三角形,
∴EM=DE,
∴EB、ED、CF能围成△EBM,
最大内角∠EBM=∠EBC+∠DBM=60°+60°=120°.
15.解:(1)如图1,延长DG至点H,使GH=DG,连接FH.
∵G是EF的中点,∴EG=FG,
在△DGE和△HGF中,,
∴△DGE≌△HGF(SAS),∴FH=DE=3.
在△DFH中,DF-FH
提示:如图2,延长AE,DC交于点F.
∵AB∥CD,∴∠CFE=∠EAB.
∵E是BC的中点∴CE=EB.
∵∠CEF=∠AEB,
∴△CEF≌△BEA(AAS),∴AB=CF.
∵AF平分∠DAB,∴∠DAF=∠EAB.
∵∠EAB=∠CFE,∴∠DAF=∠DFA,
∴AD=DF.
∵DF=DC+CF=DC+AB,
∴AD=AB+DC.
(3)AB=AF+CF.
证明:如图3,延长AE交DC的延长线于点G.
∵AB∥DG,∴∠G=∠EAB.
∵CE=EB,∠CEG=∠BEA,
∴△CEG≌△BEA(AAS),∴AB=CG.
∵AE平分∠FAB,∴∠FAG=∠EAB.
∵∠G=∠EAB,∴∠FAG=∠G,∴AF=FG.
∵CG=CF+FG=CF+AF,∴AB=AF+CF.
同课章节目录
