人教A版数学(选择性必修三讲义)第01讲6.1分类加法计数原理与分步乘法计数原理(学生版+解析)
文档属性
| 名称 | 人教A版数学(选择性必修三讲义)第01讲6.1分类加法计数原理与分步乘法计数原理(学生版+解析) | 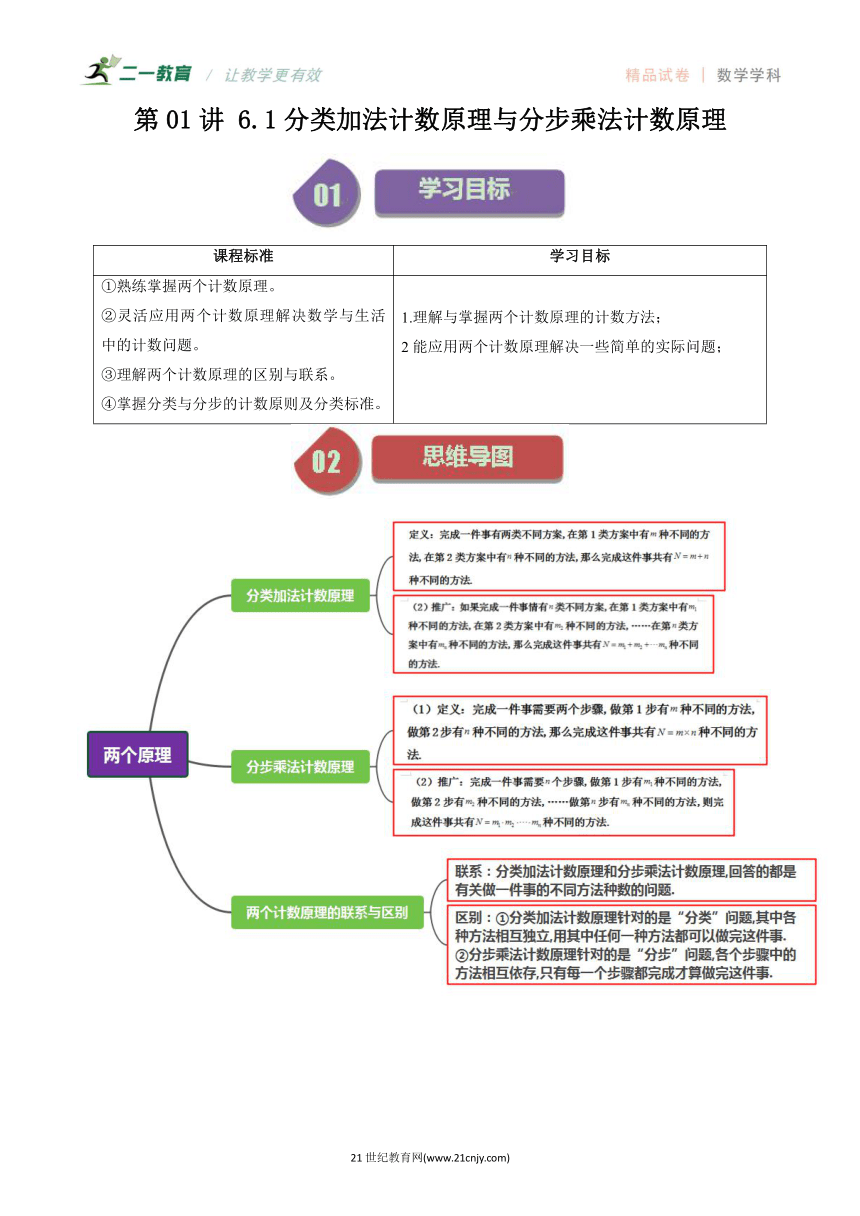 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 09:02:41 | ||
图片预览





文档简介
第01讲 6.1分类加法计数原理与分步乘法计数原理
课程标准 学习目标
①熟练掌握两个计数原理。 ②灵活应用两个计数原理解决数学与生活中的计数问题。 ③理解两个计数原理的区别与联系。 ④掌握分类与分步的计数原则及分类标准。 1.理解与掌握两个计数原理的计数方法; 2能应用两个计数原理解决一些简单的实际问题;
知识点01:分类加法计数原理
(1)定义:完成一件事有两类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:如果完成一件事情有类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,……在第类方案中有种不同的方法,那么完成这件事共有种不同的方法.
【即学即练1】(2023上·高二课时练习)音乐播放器里存有10首中文歌曲,8首英文歌曲,3首法文歌曲,任选一首歌曲进行播放,有多少种不同的选法?
【答案】
【详解】依题意一共有种选法.
知识点02:分步乘法计数原理
(1)定义:完成一件事需要两个步骤,做第1步有种不同的方法,做第2步有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:完成一件事需要个步骤,做第1步有种不同的方法,做第2步有种不同的方法,……做第步有种不同的方法,则完成这件事共有种不同的方法.
【即学即练2】(2023上·高二课时练习)一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成 个四位数号码?.
【答案】
【详解】按从左到右的顺序拨号可以分四步完成:
第1步,有10种拨号方式,
第2步,有10种拨号方式,
第3步,有10种拨号方式,
第4步,有10种拨号方式,
根据分步计数原理,共可以组成个四位数的号码.
故答案为:.
知识点03:两个计数原理的联系与区别
联系:分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题.
区别:①分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事.
②分步乘法计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有每一个步骤都完成才算做完这件事.
题型01 利用分类加法计数原理解题
【典例1】(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)完成一项工作,有两种方法,有6个人只会用第一种方法,另外有4个人只会第二种方法,从这10个人中选1个人完成这项工作,则不同的选法共有( )
A.6种 B.10种 C.4种 D.60种
【典例2】(2023上·高二课时练习)某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.推选1名优秀团员为总负责人,有 种不同的选法.
【典例3】(2023上·高二课时练习)如图,在由电键组A与B所组成的并联电路中,要接通电源,使电灯发光的方法种数是 .
【典例4】(2023·全国·高二课堂例题)某市的有线电视可以接收中央台12个频道、本地台10个频道和其他省市46个频道的节目.
(1)当这些频道播放的节目互不相同时,一台电视机共可以选看多少个不同的节目?
(2)如果有3个频道正在转播同一场球赛,其余频道正在播放互不相同的节目,一台电视机共可以选看多少个不同的节目?
【变式1】(2024·全国·高三专题练习)已知直线方程,若从0、1、2、3、5、7这六个数中每次取两个不同的数分别作为A、B的值,则可表示 条不同的直线.
【变式2】(2023上·陕西汉中·高二校联考阶段练习)已知某校高二(1)班有42人,高二(2)班有45人,高一(3)班有38人,现从这三个班中任选1人去参加活动,则不同的选法共有 种.
【变式3】(2023·全国·高三专题练习)已知集合,,在中任取一元素,在中任取一元素,组成数对,则其中的数对有多少个
题型02 利用分步乘法计数原理解题
【典例1】(2023上·山东·高二校联考阶段练习)甲同学计划从3本不同的文学书和4本不同的科学书中各选1本阅读,则不同的选法共有( )
A.81种 B.64种 C.12种 D.7种
【典例2】(2023下·高二课时练习)某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人.从4种血型的人中各选1人去献血,不同的选法种数为( )
A.1200 B.600 C.300 D.26
【典例3】(2023下·高二课时练习)在图中的电路中,仅合上2只开关接通电路,有多少种不同的方法?
【变式1】(2023上·江西南昌·高二江西师大附中校考期中)用1,2,3,4可以组成无重复数字的三位数的个数为( )
A.16 B.24 C.36 D.48
【变式2】(2023上·高二课时练习)某商场共有4个门,若从一个门进,另一个门出,不同走法的种数是( )
A.10 B.11 C.12 D.13
【变式3】(2023下·高二课时练习)现有3名老师、8名男生和5名女生共16人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A.39 B.24
C.15 D.16
题型03 两个计数原理的综合应用
【典例1】(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【典例2】(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【典例3】(2023·全国·高二课堂例题)某班班委由2位女同学、3位男同学组成,现要从该班委里选出2人去参加学校组织的培训活动,要求至少要有1位女同学参加,则不同的选法共有多少种?
【变式1】(2023上·山东临沂·高二校考阶段练习)集合,,,,5,6,,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是( )
A.2 B.4 C.5 D.6
【变式2】(2023下·山东菏泽·高二校考阶段练习)口袋中装有8个白球和10个红球每个球有不同编号,现从中取出2个球.
(1)至少有一个白球的取法有多少种?
(2)两球的颜色相同的取法有多少种?
【变式3】(2023上·高二课时练习)从a、b、c、d、e这5个元素中取出4个,放在4个不同的格子中,且元素b不能放在第二个格子里.问:一共有多少种不同的放法?
题型04 用计数原理解决涂色(种植)问题
【典例1】(2023·全国·高三专题练习)现有红、黄、蓝三种颜色,对如图所示的正五角星的内部涂色(分割成六个不同区域),要求每个区域涂一种颜色且相邻部分(有公共边的两个区域)的颜色不同,则不同的涂色方法有( )
A.48种 B.64种 C.96种 D.144种
【典例2】(2023下·山东·高二校联考阶段练习)如图,现要对某公园的4个区域进行绿化,有4种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,则不同的绿化方案有( )
A.48种 B.72种 C.64种 D.256种
【典例3】(2023·全国·高三专题练习)用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1 2
3 4
【变式1】(2023下·河北石家庄·高二石家庄市第四十一中学校考期中)在如图所示的四个区域中,有5种不同的花卉可选,每个区域只能种植一种花卉,且相邻区域花卉不同,则不同的种植方法共有 种(用数字作答)
【变式2】(2023·山西临汾·统考一模)如图,现要对某公园的4个区域进行绿化,有5种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,共有 种不同的绿化方案(用数字作答).
【变式3】(2023下·江苏常州·高二常州市北郊高级中学校考期中)如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同的种植方法总数为( )
A.12 B.18 C.24 D.30
【变式4】(2023下·高二课时练习)用6种不同的颜色为如图所示的广告牌涂色,要求在A,B,C,D四个区域中相邻(有公共边的)区域不用同一种颜色,求共有多少种不同的涂色方法?
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023上·甘肃白银·高二甘肃省靖远县第一中学校考期末)甲 乙两人从3门课程中各选修1门,则甲 乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.3种 D.9种
2.(2023下·安徽池州·高二校联考期中)“声东击西”是游击战争的一种战术:声东可以击东、南、西、北中的任意一个方向,以此灵活地打击或消灭敌人.同样还有“声南击北”等不同的战术,由此可知这类战术中打击或消灭敌人的方法总数为( )
A.16 B.12 C.4 D.3
3.(2023下·福建泉州·高二校考期末)有5名学生报名参加3项体育比赛,每人限报一项,则不同的报名方法的种数为( )
A.243 B.125 C.60 D.120
4.(2023下·黑龙江大庆·高二校考期中)完成一件事有三类不同方案,在第类方案中有种不同的方法,在第类方案中有种不同的方法,在第类方案中有种不同的方法,那么完成这件事共有种不同的方法,其中( )
A. B. C. D.
5.(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
6.(2023下·河北邯郸·高二校联考期中)有序数对满足,且使关于的方程有实数解,则这样的有序数对的个数为( )
A.15 B.14 C.13 D.10
7.(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
8.(2023下·山东德州·高一统考期末)根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.算筹计数法就是用一根根同样长短和粗细的小棍子以不同的排列方式来表示数字,如图所示.如果用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹不一样多的概率为( )
A. B. C. D.
二、多选题
9.(2023下·广东茂名·高二统考期中)现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
10.(2023下·山东枣庄·高二枣庄八中校考阶段练习)现有4个兴趣小组,第一、二、三、四组分别有6人、7人、8人、9人,则下列说法正确的是( )
A.选1人为负责人的选法种数为30
B.每组选1名组长的选法种数为3024
C.若推选2人发言,这2人需来自不同的小组,则不同的选法种数为335
D.若另有3名学生加入这4个小组,可自由选择小组,且第一组必有人选,则不同的选法有35种
三、填空题
11.(2023上·山东日照·高二日照一中校考阶段练习)某次足球比赛共12支球队参加,分三个阶段进行
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净胜球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
则全部赛程共需比赛 场.
12.(2023下·江苏扬州·高二扬州中学校考期中)已知直线中的a,b,c是取自集合中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是 .
四、解答题
13.(2023上·高二课时练习)已知某容器中,H有3种同位素,Cl有2种同位素,Na有3种同位素,O有4种同位素,试问一共可以组成多少种HCl和NaOH的分子?
14.(2023·全国·高三专题练习)用6种不同颜色的彩色粉笔写黑板报,板报设计如图所示,要求相邻区域不能用同一种颜色的彩色粉笔.若允许同一种颜色多次使用,则该板报有多少种书写方案
B能力提升
1.(2023·全国·高三专题练习)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有( )
A.648个 B.720个 C.810个 D.891个
2.(2023下·高二单元测试)算盘是中国古代的一项重要发明.现有一种算盘(如图1),共两档,自右向左分别表示个位和十位,档中横以梁,梁上一珠拨下,记作数字,梁下五珠,上拨一珠记作数字(如图2中算盘表示整数).如果拨动图1算盘中的三枚算珠,可以表示不同整数的个数为( )
A. B. C. D.
3.(2023下·山东枣庄·高二枣庄八中校考阶段练习)四色定理(Fourcolortheorem)又称四色猜想,是世界近代三大数学难题之一.它是于年由毕业于伦敦大学的格斯里(FrancisGuthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”四色问题的证明进程缓慢,直到年,美国数学家运用电子计算机证明了四色定理.某校数学兴趣小组在研究给四棱锥的各个面涂颜色时,提出如下的“四色问题”:要求相邻面(含公共棱的平面)不得使用同一颜色,现有种颜色可供选择,那么不同的涂法有( )
A.种 B.种 C.种 D.种
4.(2023上·上海浦东新·高二上海师大附中校考期末)如图所示,玩具计数算盘的三档上各有7个算珠,现将每档算珠分为左右两部分,左侧的每个算珠表示数2,右侧的每个算珠表示数1(允许一侧无珠),记上、中、下三档的数字和分别为,,. 例如,图中上档的数字和. 若,,成等差数列,则不同的分珠计数法有 种.
5.(2023·全国·高三专题练习)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图所示.将一个正四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
21世纪教育网(www.21cnjy.com)
第01讲 6.1分类加法计数原理与分步乘法计数原理
课程标准 学习目标
①熟练掌握两个计数原理。 ②灵活应用两个计数原理解决数学与生活中的计数问题。 ③理解两个计数原理的区别与联系。 ④掌握分类与分步的计数原则及分类标准。 1.理解与掌握两个计数原理的计数方法; 2能应用两个计数原理解决一些简单的实际问题;
知识点01:分类加法计数原理
(1)定义:完成一件事有两类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:如果完成一件事情有类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,……在第类方案中有种不同的方法,那么完成这件事共有种不同的方法.
【即学即练1】(2023上·高二课时练习)音乐播放器里存有10首中文歌曲,8首英文歌曲,3首法文歌曲,任选一首歌曲进行播放,有多少种不同的选法?
【答案】
【详解】依题意一共有种选法.
知识点02:分步乘法计数原理
(1)定义:完成一件事需要两个步骤,做第1步有种不同的方法,做第2步有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:完成一件事需要个步骤,做第1步有种不同的方法,做第2步有种不同的方法,……做第步有种不同的方法,则完成这件事共有种不同的方法.
【即学即练2】(2023上·高二课时练习)一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成 个四位数号码?.
【答案】
【详解】按从左到右的顺序拨号可以分四步完成:
第1步,有10种拨号方式,
第2步,有10种拨号方式,
第3步,有10种拨号方式,
第4步,有10种拨号方式,
根据分步计数原理,共可以组成个四位数的号码.
故答案为:.
知识点03:两个计数原理的联系与区别
联系:分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题.
区别:①分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事.
②分步乘法计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有每一个步骤都完成才算做完这件事.
题型01 利用分类加法计数原理解题
【典例1】(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)完成一项工作,有两种方法,有6个人只会用第一种方法,另外有4个人只会第二种方法,从这10个人中选1个人完成这项工作,则不同的选法共有( )
A.6种 B.10种 C.4种 D.60种
【答案】B
【详解】根据分类加法计数原理,6+4=10.
故选:B.
【典例2】(2023上·高二课时练习)某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.推选1名优秀团员为总负责人,有 种不同的选法.
【答案】24
【详解】第一类是从一班的8名优秀团员中产生,有8种不同的选法;
第二类是从二班的10名优秀团员中产生,有10种不同的选法;
第三类是从三班的6名优秀团员中产生,有6种不同的选法;
由分类加法计数原理可得,共有种不同的选法.
故答案为:24.
【典例3】(2023上·高二课时练习)如图,在由电键组A与B所组成的并联电路中,要接通电源,使电灯发光的方法种数是 .
【答案】5
【详解】在电键组A中有2个电键,电键组B中有3个电键,
应用分类加法计数原理,共有2+3=5种接通电源使电灯发光的方法.
故答案为:5.
【典例4】(2023·全国·高二课堂例题)某市的有线电视可以接收中央台12个频道、本地台10个频道和其他省市46个频道的节目.
(1)当这些频道播放的节目互不相同时,一台电视机共可以选看多少个不同的节目?
(2)如果有3个频道正在转播同一场球赛,其余频道正在播放互不相同的节目,一台电视机共可以选看多少个不同的节目?
【答案】(1)68
(2)66
【详解】(1)当所有频道播放的节目互不相同时,一台电视机选看的节目可分为3类:
第一类,选看中央台频道的节目,有12个不同的节目;
第二类,选看本地台频道的节目,有10个不同的节目;
第三类,选看其他省市频道的节目,有46个不同的节目.
根据分类加法计数原理,一台电视机共可以选看个不同的节目.
(2)因为有3个频道正在转播同一场球赛,即这3个频道转播的节目只有1个,
而其余频道共有个正在播放互不相同的节目,
所以一台电视机共可以选看个不同的节目.
【变式1】(2024·全国·高三专题练习)已知直线方程,若从0、1、2、3、5、7这六个数中每次取两个不同的数分别作为A、B的值,则可表示 条不同的直线.
【答案】22
【详解】当时,可表示1条直线;当时,可表示1条直线;
当时,A有5种选法,B有4种选法,可表示条不同的直线.
由分类加法计数原理,知共可表示条不同的直线.
故答案为:22
【变式2】(2023上·陕西汉中·高二校联考阶段练习)已知某校高二(1)班有42人,高二(2)班有45人,高一(3)班有38人,现从这三个班中任选1人去参加活动,则不同的选法共有 种.
【答案】125
【详解】根据分类加法计数原理,不同的选法共有种.
故答案为:125
【变式3】(2023·全国·高三专题练习)已知集合,,在中任取一元素,在中任取一元素,组成数对,则其中的数对有多少个
【答案】15
【详解】的数对可以分类来解:
当时,,有种结果;
当时,,有种结果;
当时,,有种结果;
当时,,有种结果;
当时,,有5种结果.
综上所述,共有(个)满足条件的数对.
题型02 利用分步乘法计数原理解题
【典例1】(2023上·山东·高二校联考阶段练习)甲同学计划从3本不同的文学书和4本不同的科学书中各选1本阅读,则不同的选法共有( )
A.81种 B.64种 C.12种 D.7种
【答案】C
【详解】根据分步乘法计数原理,不同的选法共有种.
故选:C
【典例2】(2023下·高二课时练习)某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人.从4种血型的人中各选1人去献血,不同的选法种数为( )
A.1200 B.600 C.300 D.26
【答案】A
【详解】分四步:
第一步,选O型血的人有10种选法;
第二步,选A型血的人有5种选法;
第三步,选B型血的人有8种选法;
第四步,选AB型血的人有3种选法.
故共有10×5×8×3
【典例3】(2023下·高二课时练习)在图中的电路中,仅合上2只开关接通电路,有多少种不同的方法?
【答案】6
【详解】在图中,按要求接通电路必须分两步进行:
第一步,合上A中的1只开关;
第二步,合上B中的1只开关.根据分步计数原理,
所以共有种不同的方法.
答:在图中的电路中,仅合上2只开关接通电 路,有6种不同的方法.
【变式1】(2023上·江西南昌·高二江西师大附中校考期中)用1,2,3,4可以组成无重复数字的三位数的个数为( )
A.16 B.24 C.36 D.48
【答案】B
【详解】先从4个数中选1个排在百位,有4种;
然后从剩下的3个数中选1个排在十位,有3种;
最后从剩下的2个数中选1个排在个位,有2种;
根据分步乘法计数原理可得组成无重复数字的三位数的个数为.
故选:B.
【变式2】(2023上·高二课时练习)某商场共有4个门,若从一个门进,另一个门出,不同走法的种数是( )
A.10 B.11 C.12 D.13
【答案】C
【详解】分两步完成,
第一步:从4个门中选择一个门进有4种方法,
第二步:从余下的3个门中选一个出有3种方法,
根据分步计数乘法原理,共有种.
故选:C
=1200(种)不同的选法.
故选:A
【变式3】(2023下·高二课时练习)现有3名老师、8名男生和5名女生共16人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A.39 B.24
C.15 D.16
【答案】A
【详解】先从3名老师中任选1名,有3种选法,再从13名学生中任选1名,有13种选法.由分步乘法计数原理知,不同的选法种数为3×13=39.故选:A
题型03 两个计数原理的综合应用
【典例1】(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【答案】D
【详解】按顶点处标注的数字分类,有如下几种情况:
若处都标注的是4,则处的标注方法有(种);
若处都标注的是3,则处的标注方法有(种);
若处都标注的是2,则处的标注方法有1种;
若处标注的是4和3两个数字,则处的标注方法有(种),不同的标注方法共有(种);
若处标注的是4和2两个数字,则处的标注方法有1种,不同的标注方法共有(种);
若处标注的是3和2两个数字,则处的标注方法有1种,不同的标注方法共有(种).
由分类加法计数原理可知,顶点处的数字都大于顶点处的数字的标注方法共有(种).
故选:D.
【典例2】(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【答案】D
【详解】正方体的两个顶点确定的直线有棱、面对角线、体对角线,
对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有(个);
对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个,
不存在四个顶点确定的平面与体对角线垂直,
所以正方体中“正交线面对”共有(个).
故选:D
【典例3】(2023·全国·高二课堂例题)某班班委由2位女同学、3位男同学组成,现要从该班委里选出2人去参加学校组织的培训活动,要求至少要有1位女同学参加,则不同的选法共有多少种?
【答案】7
【详解】按照选择的女同学人数分为两种情况,即2名都是女同学和只有1名女同学.
第1类:2名都是女同学的选法显然只有1种.
第2类:只有1名女同学的选法,可以分为两步完成:先从2名女同学中选出1人,有2种选法;
再从3位男同学中选出1人,有3种选法.依据分步乘法计数原理,共有不同的安排方法种.
依据分类加法计数原理,不同的选法共有种.
【变式1】(2023上·山东临沂·高二校考阶段练习)集合,,,,5,6,,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是( )
A.2 B.4 C.5 D.6
【答案】D
【详解】第二象限的横坐标是负数,纵坐标是正数.
若集合提供横坐标,集合提供纵坐标,则有,
若集合提供纵坐标,集合提供横坐标,则有,合计,
即这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是6个,
故选:D.
【变式2】(2023下·山东菏泽·高二校考阶段练习)口袋中装有8个白球和10个红球每个球有不同编号,现从中取出2个球.
(1)至少有一个白球的取法有多少种?
(2)两球的颜色相同的取法有多少种?
【答案】(1)
(2)
【详解】(1)根据题意分2类完成任务:
第一类:白球红球各一个有种,第二类:均为白球,种,
所以共有种;
(2)根据题意分2类完成任务:
第一类:均为白球,种,第二类:均为红球,种,
所以共有种.
【变式3】(2023上·高二课时练习)从a、b、c、d、e这5个元素中取出4个,放在4个不同的格子中,且元素b不能放在第二个格子里.问:一共有多少种不同的放法?
【答案】
【详解】元素b不被取出,不同的放法有种,
当元素b被取出,则元素b有三个位置,不同的放法有种,
所以一共有种不同的放法.
题型04 用计数原理解决涂色(种植)问题
【典例1】(2023·全国·高三专题练习)现有红、黄、蓝三种颜色,对如图所示的正五角星的内部涂色(分割成六个不同区域),要求每个区域涂一种颜色且相邻部分(有公共边的两个区域)的颜色不同,则不同的涂色方法有( )
A.48种 B.64种 C.96种 D.144种
【答案】C
【详解】根据题意,假设正五角星的区域为,,,,,,如图所示,
先对区域涂色,有3种方法,再对,,,,这5个区域进行涂色,
∵,,,,这5个区域都与相邻,∴每个区域都有2种涂色方法,
∴共有种涂色方法.故选C.
【典例2】(2023下·山东·高二校联考阶段练习)如图,现要对某公园的4个区域进行绿化,有4种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,则不同的绿化方案有( )
A.48种 B.72种 C.64种 D.256种
【答案】A
【详解】从A开始摆放花卉,A有4种颜色花卉摆放方法,
C有3种颜色花卉摆放方法,B有2种颜色花卉摆放方法;
由D区与A,B花卉颜色不一样,与C区花卉颜色可以同色也可以不同色,
则D有2种颜色花卉摆放方法.
故共有种绿化方案.
故选:A
【典例3】(2023·全国·高三专题练习)用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1 2
3 4
【答案】260
【详解】第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
【变式1】(2023下·河北石家庄·高二石家庄市第四十一中学校考期中)在如图所示的四个区域中,有5种不同的花卉可选,每个区域只能种植一种花卉,且相邻区域花卉不同,则不同的种植方法共有 种(用数字作答)
【答案】240
【详解】由分步乘法计数原理得种,
故答案为:240.
【变式2】(2023·山西临汾·统考一模)如图,现要对某公园的4个区域进行绿化,有5种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,共有 种不同的绿化方案(用数字作答).
【答案】180
【详解】如图:
A B D
C
从A开始摆放花卉,A有5种颜色花卉摆放方法,
B有4种颜色花卉摆放方法,C有3种颜色花卉摆放方法;
由D区与B,C花卉颜色不一样,与A区花卉颜色可以同色也可以不同色,
则D有3种颜色花卉摆放方法.
故共有种涂色方法.
故答案为:180
【变式3】(2023下·江苏常州·高二常州市北郊高级中学校考期中)如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同的种植方法总数为( )
A.12 B.18 C.24 D.30
【答案】B
【详解】根据题意,分3步进行分析:
(1)对于块,可以在3种不同的花中任选1种,有种情况;
(2)对于块,可以在剩下的2种不同的花中任选1种,有种情况;
(3)对于C 、D块,分2种情况:
若D块与块相同,则C块可以在其余的2种不同的花中任选1种,有种情况,
若D块与块不相同,则块有1种情况,块有1种情况,此时C 、D有1种情况,
则C 、D共有种情况;
综合可得:一共有种不同的种法.
故选:B
【变式4】(2023下·高二课时练习)用6种不同的颜色为如图所示的广告牌涂色,要求在A,B,C,D四个区域中相邻(有公共边的)区域不用同一种颜色,求共有多少种不同的涂色方法?
【答案】480(种)
【详解】方法一:分类计数,
第一类,A,D涂同色,有6×5×4=120(种)涂法,
第二类,A,D涂异色,有6×5×4×3=360(种)涂法,
共有120+360=480(种)涂法.
方法二:分步计数,先涂B区,有6种涂法,再涂C区,有5种涂法,最后涂A,D区域,各有4种涂法,
所以共有6×5×4×4=480(种)涂法.
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023上·甘肃白银·高二甘肃省靖远县第一中学校考期末)甲 乙两人从3门课程中各选修1门,则甲 乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.3种 D.9种
【答案】A
【分析】根据分步乘法计数原理求得正确答案.
【详解】甲 乙两人从3门课程中各选修1门,
由乘法原理可得甲 乙所选的课程不相同的选法有(种).
故选:A
2.(2023下·安徽池州·高二校联考期中)“声东击西”是游击战争的一种战术:声东可以击东、南、西、北中的任意一个方向,以此灵活地打击或消灭敌人.同样还有“声南击北”等不同的战术,由此可知这类战术中打击或消灭敌人的方法总数为( )
A.16 B.12 C.4 D.3
【答案】A
【分析】根据题意,分析声和击的情况,再由分步乘法计数原理可得答案.
【详解】根据题意,声的情况有4种,击的情况也有4种,所以这类战术中打击或消灭敌人的方法总数为.
故选:A.
3.(2023下·福建泉州·高二校考期末)有5名学生报名参加3项体育比赛,每人限报一项,则不同的报名方法的种数为( )
A.243 B.125 C.60 D.120
【答案】A
【分析】根据分步乘法计数原理求得正确答案.
【详解】每名学生都有种选择方法,
所以不同的报名方法的种数为.
故选:A
4.(2023下·黑龙江大庆·高二校考期中)完成一件事有三类不同方案,在第类方案中有种不同的方法,在第类方案中有种不同的方法,在第类方案中有种不同的方法,那么完成这件事共有种不同的方法,其中( )
A. B. C. D.
【答案】A
【分析】根据分类加法计数原理直接求解即可.
【详解】由分类加法计数原理得:.
故选:A.
5.(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【答案】D
【分析】根据给定条件,利用分类加法计数原理列式计算作答.
【详解】正方体的两个顶点确定的直线有棱、面对角线、体对角线,
对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有(个);
对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个,
不存在四个顶点确定的平面与体对角线垂直,
所以正方体中“正交线面对”共有(个).
故选:D
6.(2023下·河北邯郸·高二校联考期中)有序数对满足,且使关于的方程有实数解,则这样的有序数对的个数为( )
A.15 B.14 C.13 D.10
【答案】A
【分析】分情况讨论即可计算有序数对的个数.
【详解】(1)当时,有为实根,则有4种可能;
(2)当时,方程有实根,所以,所以.
当时,有4种.
当时,有4种.
当时,有3种.
所以,有序数对的个数为.
故选:A.
7.(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【答案】D
【分析】按顶点处标注的数字分类讨论 ,利用分类加法和乘法计数原理即可求解.
【详解】按顶点处标注的数字分类,有如下几种情况:
若处都标注的是4,则处的标注方法有(种);
若处都标注的是3,则处的标注方法有(种);
若处都标注的是2,则处的标注方法有1种;
若处标注的是4和3两个数字,则处的标注方法有(种),不同的标注方法共有(种);
若处标注的是4和2两个数字,则处的标注方法有1种,不同的标注方法共有(种);
若处标注的是3和2两个数字,则处的标注方法有1种,不同的标注方法共有(种).
由分类加法计数原理可知,顶点处的数字都大于顶点处的数字的标注方法共有(种).
故选:D.
8.(2023下·山东德州·高一统考期末)根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.算筹计数法就是用一根根同样长短和粗细的小棍子以不同的排列方式来表示数字,如图所示.如果用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹不一样多的概率为( )
A. B. C. D.
【答案】B
【分析】先求出一共摆出的两位数的个数,再求出个位和十位上的算筹不一样多的两位数的个数,利用古典概型概率公式计算即可.
【详解】用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,
共可以摆出个两位数,其中个位和十位上的算筹都为1有种,
个位和十位上的算筹都为2有种,个位和十位上的算筹都为3有种,
个位和十位上的算筹都为4有种,个位和十位上的算筹都为5有种,
共有种,所以个位和十位上的算筹不一样多的有种,
所以个位和十位上的算筹不一样多的概率为.
故选:B
二、多选题
9.(2023下·广东茂名·高二统考期中)现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
【答案】ABD
【分析】利用排列知识计算得到选项ABD正确;若要选出不同颜色的2个球,有种不同的选法,所以选项C错误.
【详解】解:A. 从中任选1个球,有15种不同的选法,所以该选项正确;
B. 若每种颜色选出1个球,有120种不同的选法,所以该选项正确;
C. 若要选出不同颜色的2个球,有种不同的选法,所以该选项错误;
D. 若要不放回地依次选出2个球,有210种不同的选法,所以该选项正确.
故选:ABD
10.(2023下·山东枣庄·高二枣庄八中校考阶段练习)现有4个兴趣小组,第一、二、三、四组分别有6人、7人、8人、9人,则下列说法正确的是( )
A.选1人为负责人的选法种数为30
B.每组选1名组长的选法种数为3024
C.若推选2人发言,这2人需来自不同的小组,则不同的选法种数为335
D.若另有3名学生加入这4个小组,可自由选择小组,且第一组必有人选,则不同的选法有35种
【答案】ABC
【分析】利用加法计数原理判断选项A;利用乘法计数原理判断选项B;利用乘法及加法计数原理判断选项C;利用间接法并结合乘法计数原理判断选项D.
【详解】对于A,选1人为负责人的选法种数:,故A正确;
对于B,每组选1名组长的选法:,故B正确;
对于C,2人需来自不同的小组的选法:,故C正确;
对于D,依题意:若不考虑限制,每个人有4种选择,共有种选择,若第一组没有人选,每个人有3种选择,共有种选择,
所以不同的选法有:,故D错误;
故选:ABC.
三、填空题
11.(2023上·山东日照·高二日照一中校考阶段练习)某次足球比赛共12支球队参加,分三个阶段进行
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净胜球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
则全部赛程共需比赛 场.
【答案】
【分析】分别计算出小组赛、半决赛、决赛需要比赛场数即可得.
【详解】小组赛中每组6队进行单循环比赛,则需比赛场,
半决赛中共需场,
决赛需场,
故共需场.
故答案为:.
12.(2023下·江苏扬州·高二扬州中学校考期中)已知直线中的a,b,c是取自集合中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是 .
【答案】11
【分析】设倾斜角为,由,对分情况讨论,利用计数原理计算即可.
【详解】设倾斜角为,,则,不妨设,则,
若,a有2种取法,b有2种取法,排除1个重复(与),故这样的直线有条;
若,a有2种取法,b有2种取法,c有2种取法,且其中任两条直线均不相同,故这样的直线有条,
从而,符合要求的直线有条.
故答案为:11.
四、解答题
13.(2023上·高二课时练习)已知某容器中,H有3种同位素,Cl有2种同位素,Na有3种同位素,O有4种同位素,试问一共可以组成多少种HCl和NaOH的分子?
【答案】一共可以组成6种HCl分子,和36种NaOH的分子
【分析】根据分步计数原理求解即可.
【详解】因为HCl由H和Cl组成,且H有3种同位素,Cl有2种同位素,故可以组成种HCl.
因为NaOH由Na和OH组成,且Na有3种同位素,O有4种同位素,H有3种同位素,故OH有种情况,
故可以组成种NaOH的分子.
14.(2023·全国·高三专题练习)用6种不同颜色的彩色粉笔写黑板报,板报设计如图所示,要求相邻区域不能用同一种颜色的彩色粉笔.若允许同一种颜色多次使用,则该板报有多少种书写方案
【答案】600
【分析】根据分步相乘计数原理求解即可.
【详解】第一步,选英语角用的彩色粉笔,有6种不同的选法;
第二步,选语文学苑用的彩色粉笔,不能与英语角相同,有5种不同的选法;
第三步,选理综世界用的彩色粉笔,与英语角和语文学苑用的颜色都不相同,有4种不同的选法;
第四步,选数学天地用的彩色粉笔,只要与理综世界不同即可,有5种不同的选法.
由分步乘法计数原理知,共有种不同的书写方案.
B能力提升
1.(2023·全国·高三专题练习)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有( )
A.648个 B.720个 C.810个 D.891个
【答案】D
【分析】5位“回文数”的万位与个位相同,千位与十位相同,所以只需确定前3位即可.
【详解】根据“回文数”的特点,只需确定前3位即可,最高位即万位有9种排法,千位和百位各有10种排法,根据分步乘法计数原理,共有种排法,其中各位数字相同的共有9种,则所有5位数中是“回文数”且各位数字不全相同的共有种.
故选:D.
2.(2023下·高二单元测试)算盘是中国古代的一项重要发明.现有一种算盘(如图1),共两档,自右向左分别表示个位和十位,档中横以梁,梁上一珠拨下,记作数字,梁下五珠,上拨一珠记作数字(如图2中算盘表示整数).如果拨动图1算盘中的三枚算珠,可以表示不同整数的个数为( )
A. B. C. D.
【答案】C
【分析】分四种情况讨论:①个位拨动三枚;②十位拨动一枚,个位拨动两枚;③十位拨动两枚,个位拨动一枚;④十位拨动三枚.分别列举出每种情况下对应的数字,利用分类加法计数原理可得结果.
【详解】由题意,拨动三枚算珠,有种拨法:
①个位拨动三枚,有种结果:、;
②十位拨动一枚,个位拨动两枚,有种结果:、、、;
③十位拨动两枚,个位拨动一枚,有种结果:、、、;
④十位拨动三枚,有种结果:、.
综上,拨动题图1算盘中的三枚算珠,可以表示不同整数的个数为.
故选:C.
3.(2023下·山东枣庄·高二枣庄八中校考阶段练习)四色定理(Fourcolortheorem)又称四色猜想,是世界近代三大数学难题之一.它是于年由毕业于伦敦大学的格斯里(FrancisGuthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”四色问题的证明进程缓慢,直到年,美国数学家运用电子计算机证明了四色定理.某校数学兴趣小组在研究给四棱锥的各个面涂颜色时,提出如下的“四色问题”:要求相邻面(含公共棱的平面)不得使用同一颜色,现有种颜色可供选择,那么不同的涂法有( )
A.种 B.种 C.种 D.种
【答案】B
【分析】先确定底面的涂色种数,然后依次确定侧面、平面的涂色方法种数,对侧面与侧面的所涂颜色是否相同进行分类讨论,确定侧面的涂色方法种数,利用分步和分类计数原理可得结果.
【详解】如下图所示:
底面的涂色有种选择,侧面有种选择,侧面有2种选择.
①若侧面与侧面所涂颜色相同,则侧面有种选择;
②若侧面与侧面所涂颜色不同,则侧面有种选择,侧面有种选择.
综上所述,不同的涂法种数为种.
故选:B.
4.(2023上·上海浦东新·高二上海师大附中校考期末)如图所示,玩具计数算盘的三档上各有7个算珠,现将每档算珠分为左右两部分,左侧的每个算珠表示数2,右侧的每个算珠表示数1(允许一侧无珠),记上、中、下三档的数字和分别为,,. 例如,图中上档的数字和. 若,,成等差数列,则不同的分珠计数法有 种.
【答案】32
【分析】先确定每档可取的整数,再根据公差分类讨论,最后根据分类计数原理得结果.
【详解】每档可取7到14中的每个整数,
若公差为0,共有8种;
若公差为±1,则共有12种;
若公差为±2,则共有8种;
若公差为±3,则共有4种;
所以,不同分珠方法有:8+12+8+4=32种,
故答案为32
【点睛】本题考查分类计数原理,考查基本分析求解能力,属难题.
5.(2023·全国·高三专题练习)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图所示.将一个正四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
【答案】420
【分析】分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解
【详解】由题设,四棱锥S - ABCD的顶点S, A, B所染的颜色互不相同,它们共有种染色方法;
当染好时,不妨设所染颜色依次为1, 2, 3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S, A, B染好时,C, D还有7种染法.
故不同的染色方法有种.
21世纪教育网(www.21cnjy.com)
课程标准 学习目标
①熟练掌握两个计数原理。 ②灵活应用两个计数原理解决数学与生活中的计数问题。 ③理解两个计数原理的区别与联系。 ④掌握分类与分步的计数原则及分类标准。 1.理解与掌握两个计数原理的计数方法; 2能应用两个计数原理解决一些简单的实际问题;
知识点01:分类加法计数原理
(1)定义:完成一件事有两类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:如果完成一件事情有类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,……在第类方案中有种不同的方法,那么完成这件事共有种不同的方法.
【即学即练1】(2023上·高二课时练习)音乐播放器里存有10首中文歌曲,8首英文歌曲,3首法文歌曲,任选一首歌曲进行播放,有多少种不同的选法?
【答案】
【详解】依题意一共有种选法.
知识点02:分步乘法计数原理
(1)定义:完成一件事需要两个步骤,做第1步有种不同的方法,做第2步有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:完成一件事需要个步骤,做第1步有种不同的方法,做第2步有种不同的方法,……做第步有种不同的方法,则完成这件事共有种不同的方法.
【即学即练2】(2023上·高二课时练习)一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成 个四位数号码?.
【答案】
【详解】按从左到右的顺序拨号可以分四步完成:
第1步,有10种拨号方式,
第2步,有10种拨号方式,
第3步,有10种拨号方式,
第4步,有10种拨号方式,
根据分步计数原理,共可以组成个四位数的号码.
故答案为:.
知识点03:两个计数原理的联系与区别
联系:分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题.
区别:①分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事.
②分步乘法计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有每一个步骤都完成才算做完这件事.
题型01 利用分类加法计数原理解题
【典例1】(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)完成一项工作,有两种方法,有6个人只会用第一种方法,另外有4个人只会第二种方法,从这10个人中选1个人完成这项工作,则不同的选法共有( )
A.6种 B.10种 C.4种 D.60种
【典例2】(2023上·高二课时练习)某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.推选1名优秀团员为总负责人,有 种不同的选法.
【典例3】(2023上·高二课时练习)如图,在由电键组A与B所组成的并联电路中,要接通电源,使电灯发光的方法种数是 .
【典例4】(2023·全国·高二课堂例题)某市的有线电视可以接收中央台12个频道、本地台10个频道和其他省市46个频道的节目.
(1)当这些频道播放的节目互不相同时,一台电视机共可以选看多少个不同的节目?
(2)如果有3个频道正在转播同一场球赛,其余频道正在播放互不相同的节目,一台电视机共可以选看多少个不同的节目?
【变式1】(2024·全国·高三专题练习)已知直线方程,若从0、1、2、3、5、7这六个数中每次取两个不同的数分别作为A、B的值,则可表示 条不同的直线.
【变式2】(2023上·陕西汉中·高二校联考阶段练习)已知某校高二(1)班有42人,高二(2)班有45人,高一(3)班有38人,现从这三个班中任选1人去参加活动,则不同的选法共有 种.
【变式3】(2023·全国·高三专题练习)已知集合,,在中任取一元素,在中任取一元素,组成数对,则其中的数对有多少个
题型02 利用分步乘法计数原理解题
【典例1】(2023上·山东·高二校联考阶段练习)甲同学计划从3本不同的文学书和4本不同的科学书中各选1本阅读,则不同的选法共有( )
A.81种 B.64种 C.12种 D.7种
【典例2】(2023下·高二课时练习)某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人.从4种血型的人中各选1人去献血,不同的选法种数为( )
A.1200 B.600 C.300 D.26
【典例3】(2023下·高二课时练习)在图中的电路中,仅合上2只开关接通电路,有多少种不同的方法?
【变式1】(2023上·江西南昌·高二江西师大附中校考期中)用1,2,3,4可以组成无重复数字的三位数的个数为( )
A.16 B.24 C.36 D.48
【变式2】(2023上·高二课时练习)某商场共有4个门,若从一个门进,另一个门出,不同走法的种数是( )
A.10 B.11 C.12 D.13
【变式3】(2023下·高二课时练习)现有3名老师、8名男生和5名女生共16人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A.39 B.24
C.15 D.16
题型03 两个计数原理的综合应用
【典例1】(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【典例2】(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【典例3】(2023·全国·高二课堂例题)某班班委由2位女同学、3位男同学组成,现要从该班委里选出2人去参加学校组织的培训活动,要求至少要有1位女同学参加,则不同的选法共有多少种?
【变式1】(2023上·山东临沂·高二校考阶段练习)集合,,,,5,6,,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是( )
A.2 B.4 C.5 D.6
【变式2】(2023下·山东菏泽·高二校考阶段练习)口袋中装有8个白球和10个红球每个球有不同编号,现从中取出2个球.
(1)至少有一个白球的取法有多少种?
(2)两球的颜色相同的取法有多少种?
【变式3】(2023上·高二课时练习)从a、b、c、d、e这5个元素中取出4个,放在4个不同的格子中,且元素b不能放在第二个格子里.问:一共有多少种不同的放法?
题型04 用计数原理解决涂色(种植)问题
【典例1】(2023·全国·高三专题练习)现有红、黄、蓝三种颜色,对如图所示的正五角星的内部涂色(分割成六个不同区域),要求每个区域涂一种颜色且相邻部分(有公共边的两个区域)的颜色不同,则不同的涂色方法有( )
A.48种 B.64种 C.96种 D.144种
【典例2】(2023下·山东·高二校联考阶段练习)如图,现要对某公园的4个区域进行绿化,有4种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,则不同的绿化方案有( )
A.48种 B.72种 C.64种 D.256种
【典例3】(2023·全国·高三专题练习)用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1 2
3 4
【变式1】(2023下·河北石家庄·高二石家庄市第四十一中学校考期中)在如图所示的四个区域中,有5种不同的花卉可选,每个区域只能种植一种花卉,且相邻区域花卉不同,则不同的种植方法共有 种(用数字作答)
【变式2】(2023·山西临汾·统考一模)如图,现要对某公园的4个区域进行绿化,有5种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,共有 种不同的绿化方案(用数字作答).
【变式3】(2023下·江苏常州·高二常州市北郊高级中学校考期中)如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同的种植方法总数为( )
A.12 B.18 C.24 D.30
【变式4】(2023下·高二课时练习)用6种不同的颜色为如图所示的广告牌涂色,要求在A,B,C,D四个区域中相邻(有公共边的)区域不用同一种颜色,求共有多少种不同的涂色方法?
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023上·甘肃白银·高二甘肃省靖远县第一中学校考期末)甲 乙两人从3门课程中各选修1门,则甲 乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.3种 D.9种
2.(2023下·安徽池州·高二校联考期中)“声东击西”是游击战争的一种战术:声东可以击东、南、西、北中的任意一个方向,以此灵活地打击或消灭敌人.同样还有“声南击北”等不同的战术,由此可知这类战术中打击或消灭敌人的方法总数为( )
A.16 B.12 C.4 D.3
3.(2023下·福建泉州·高二校考期末)有5名学生报名参加3项体育比赛,每人限报一项,则不同的报名方法的种数为( )
A.243 B.125 C.60 D.120
4.(2023下·黑龙江大庆·高二校考期中)完成一件事有三类不同方案,在第类方案中有种不同的方法,在第类方案中有种不同的方法,在第类方案中有种不同的方法,那么完成这件事共有种不同的方法,其中( )
A. B. C. D.
5.(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
6.(2023下·河北邯郸·高二校联考期中)有序数对满足,且使关于的方程有实数解,则这样的有序数对的个数为( )
A.15 B.14 C.13 D.10
7.(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
8.(2023下·山东德州·高一统考期末)根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.算筹计数法就是用一根根同样长短和粗细的小棍子以不同的排列方式来表示数字,如图所示.如果用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹不一样多的概率为( )
A. B. C. D.
二、多选题
9.(2023下·广东茂名·高二统考期中)现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
10.(2023下·山东枣庄·高二枣庄八中校考阶段练习)现有4个兴趣小组,第一、二、三、四组分别有6人、7人、8人、9人,则下列说法正确的是( )
A.选1人为负责人的选法种数为30
B.每组选1名组长的选法种数为3024
C.若推选2人发言,这2人需来自不同的小组,则不同的选法种数为335
D.若另有3名学生加入这4个小组,可自由选择小组,且第一组必有人选,则不同的选法有35种
三、填空题
11.(2023上·山东日照·高二日照一中校考阶段练习)某次足球比赛共12支球队参加,分三个阶段进行
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净胜球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
则全部赛程共需比赛 场.
12.(2023下·江苏扬州·高二扬州中学校考期中)已知直线中的a,b,c是取自集合中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是 .
四、解答题
13.(2023上·高二课时练习)已知某容器中,H有3种同位素,Cl有2种同位素,Na有3种同位素,O有4种同位素,试问一共可以组成多少种HCl和NaOH的分子?
14.(2023·全国·高三专题练习)用6种不同颜色的彩色粉笔写黑板报,板报设计如图所示,要求相邻区域不能用同一种颜色的彩色粉笔.若允许同一种颜色多次使用,则该板报有多少种书写方案
B能力提升
1.(2023·全国·高三专题练习)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有( )
A.648个 B.720个 C.810个 D.891个
2.(2023下·高二单元测试)算盘是中国古代的一项重要发明.现有一种算盘(如图1),共两档,自右向左分别表示个位和十位,档中横以梁,梁上一珠拨下,记作数字,梁下五珠,上拨一珠记作数字(如图2中算盘表示整数).如果拨动图1算盘中的三枚算珠,可以表示不同整数的个数为( )
A. B. C. D.
3.(2023下·山东枣庄·高二枣庄八中校考阶段练习)四色定理(Fourcolortheorem)又称四色猜想,是世界近代三大数学难题之一.它是于年由毕业于伦敦大学的格斯里(FrancisGuthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”四色问题的证明进程缓慢,直到年,美国数学家运用电子计算机证明了四色定理.某校数学兴趣小组在研究给四棱锥的各个面涂颜色时,提出如下的“四色问题”:要求相邻面(含公共棱的平面)不得使用同一颜色,现有种颜色可供选择,那么不同的涂法有( )
A.种 B.种 C.种 D.种
4.(2023上·上海浦东新·高二上海师大附中校考期末)如图所示,玩具计数算盘的三档上各有7个算珠,现将每档算珠分为左右两部分,左侧的每个算珠表示数2,右侧的每个算珠表示数1(允许一侧无珠),记上、中、下三档的数字和分别为,,. 例如,图中上档的数字和. 若,,成等差数列,则不同的分珠计数法有 种.
5.(2023·全国·高三专题练习)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图所示.将一个正四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
21世纪教育网(www.21cnjy.com)
第01讲 6.1分类加法计数原理与分步乘法计数原理
课程标准 学习目标
①熟练掌握两个计数原理。 ②灵活应用两个计数原理解决数学与生活中的计数问题。 ③理解两个计数原理的区别与联系。 ④掌握分类与分步的计数原则及分类标准。 1.理解与掌握两个计数原理的计数方法; 2能应用两个计数原理解决一些简单的实际问题;
知识点01:分类加法计数原理
(1)定义:完成一件事有两类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:如果完成一件事情有类不同方案,在第1类方案中有种不同的方法,在第2类方案中有种不同的方法,……在第类方案中有种不同的方法,那么完成这件事共有种不同的方法.
【即学即练1】(2023上·高二课时练习)音乐播放器里存有10首中文歌曲,8首英文歌曲,3首法文歌曲,任选一首歌曲进行播放,有多少种不同的选法?
【答案】
【详解】依题意一共有种选法.
知识点02:分步乘法计数原理
(1)定义:完成一件事需要两个步骤,做第1步有种不同的方法,做第2步有种不同的方法,那么完成这件事共有种不同的方法.
(2)推广:完成一件事需要个步骤,做第1步有种不同的方法,做第2步有种不同的方法,……做第步有种不同的方法,则完成这件事共有种不同的方法.
【即学即练2】(2023上·高二课时练习)一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成 个四位数号码?.
【答案】
【详解】按从左到右的顺序拨号可以分四步完成:
第1步,有10种拨号方式,
第2步,有10种拨号方式,
第3步,有10种拨号方式,
第4步,有10种拨号方式,
根据分步计数原理,共可以组成个四位数的号码.
故答案为:.
知识点03:两个计数原理的联系与区别
联系:分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题.
区别:①分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事.
②分步乘法计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有每一个步骤都完成才算做完这件事.
题型01 利用分类加法计数原理解题
【典例1】(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)完成一项工作,有两种方法,有6个人只会用第一种方法,另外有4个人只会第二种方法,从这10个人中选1个人完成这项工作,则不同的选法共有( )
A.6种 B.10种 C.4种 D.60种
【答案】B
【详解】根据分类加法计数原理,6+4=10.
故选:B.
【典例2】(2023上·高二课时练习)某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.推选1名优秀团员为总负责人,有 种不同的选法.
【答案】24
【详解】第一类是从一班的8名优秀团员中产生,有8种不同的选法;
第二类是从二班的10名优秀团员中产生,有10种不同的选法;
第三类是从三班的6名优秀团员中产生,有6种不同的选法;
由分类加法计数原理可得,共有种不同的选法.
故答案为:24.
【典例3】(2023上·高二课时练习)如图,在由电键组A与B所组成的并联电路中,要接通电源,使电灯发光的方法种数是 .
【答案】5
【详解】在电键组A中有2个电键,电键组B中有3个电键,
应用分类加法计数原理,共有2+3=5种接通电源使电灯发光的方法.
故答案为:5.
【典例4】(2023·全国·高二课堂例题)某市的有线电视可以接收中央台12个频道、本地台10个频道和其他省市46个频道的节目.
(1)当这些频道播放的节目互不相同时,一台电视机共可以选看多少个不同的节目?
(2)如果有3个频道正在转播同一场球赛,其余频道正在播放互不相同的节目,一台电视机共可以选看多少个不同的节目?
【答案】(1)68
(2)66
【详解】(1)当所有频道播放的节目互不相同时,一台电视机选看的节目可分为3类:
第一类,选看中央台频道的节目,有12个不同的节目;
第二类,选看本地台频道的节目,有10个不同的节目;
第三类,选看其他省市频道的节目,有46个不同的节目.
根据分类加法计数原理,一台电视机共可以选看个不同的节目.
(2)因为有3个频道正在转播同一场球赛,即这3个频道转播的节目只有1个,
而其余频道共有个正在播放互不相同的节目,
所以一台电视机共可以选看个不同的节目.
【变式1】(2024·全国·高三专题练习)已知直线方程,若从0、1、2、3、5、7这六个数中每次取两个不同的数分别作为A、B的值,则可表示 条不同的直线.
【答案】22
【详解】当时,可表示1条直线;当时,可表示1条直线;
当时,A有5种选法,B有4种选法,可表示条不同的直线.
由分类加法计数原理,知共可表示条不同的直线.
故答案为:22
【变式2】(2023上·陕西汉中·高二校联考阶段练习)已知某校高二(1)班有42人,高二(2)班有45人,高一(3)班有38人,现从这三个班中任选1人去参加活动,则不同的选法共有 种.
【答案】125
【详解】根据分类加法计数原理,不同的选法共有种.
故答案为:125
【变式3】(2023·全国·高三专题练习)已知集合,,在中任取一元素,在中任取一元素,组成数对,则其中的数对有多少个
【答案】15
【详解】的数对可以分类来解:
当时,,有种结果;
当时,,有种结果;
当时,,有种结果;
当时,,有种结果;
当时,,有5种结果.
综上所述,共有(个)满足条件的数对.
题型02 利用分步乘法计数原理解题
【典例1】(2023上·山东·高二校联考阶段练习)甲同学计划从3本不同的文学书和4本不同的科学书中各选1本阅读,则不同的选法共有( )
A.81种 B.64种 C.12种 D.7种
【答案】C
【详解】根据分步乘法计数原理,不同的选法共有种.
故选:C
【典例2】(2023下·高二课时练习)某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人.从4种血型的人中各选1人去献血,不同的选法种数为( )
A.1200 B.600 C.300 D.26
【答案】A
【详解】分四步:
第一步,选O型血的人有10种选法;
第二步,选A型血的人有5种选法;
第三步,选B型血的人有8种选法;
第四步,选AB型血的人有3种选法.
故共有10×5×8×3
【典例3】(2023下·高二课时练习)在图中的电路中,仅合上2只开关接通电路,有多少种不同的方法?
【答案】6
【详解】在图中,按要求接通电路必须分两步进行:
第一步,合上A中的1只开关;
第二步,合上B中的1只开关.根据分步计数原理,
所以共有种不同的方法.
答:在图中的电路中,仅合上2只开关接通电 路,有6种不同的方法.
【变式1】(2023上·江西南昌·高二江西师大附中校考期中)用1,2,3,4可以组成无重复数字的三位数的个数为( )
A.16 B.24 C.36 D.48
【答案】B
【详解】先从4个数中选1个排在百位,有4种;
然后从剩下的3个数中选1个排在十位,有3种;
最后从剩下的2个数中选1个排在个位,有2种;
根据分步乘法计数原理可得组成无重复数字的三位数的个数为.
故选:B.
【变式2】(2023上·高二课时练习)某商场共有4个门,若从一个门进,另一个门出,不同走法的种数是( )
A.10 B.11 C.12 D.13
【答案】C
【详解】分两步完成,
第一步:从4个门中选择一个门进有4种方法,
第二步:从余下的3个门中选一个出有3种方法,
根据分步计数乘法原理,共有种.
故选:C
=1200(种)不同的选法.
故选:A
【变式3】(2023下·高二课时练习)现有3名老师、8名男生和5名女生共16人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A.39 B.24
C.15 D.16
【答案】A
【详解】先从3名老师中任选1名,有3种选法,再从13名学生中任选1名,有13种选法.由分步乘法计数原理知,不同的选法种数为3×13=39.故选:A
题型03 两个计数原理的综合应用
【典例1】(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【答案】D
【详解】按顶点处标注的数字分类,有如下几种情况:
若处都标注的是4,则处的标注方法有(种);
若处都标注的是3,则处的标注方法有(种);
若处都标注的是2,则处的标注方法有1种;
若处标注的是4和3两个数字,则处的标注方法有(种),不同的标注方法共有(种);
若处标注的是4和2两个数字,则处的标注方法有1种,不同的标注方法共有(种);
若处标注的是3和2两个数字,则处的标注方法有1种,不同的标注方法共有(种).
由分类加法计数原理可知,顶点处的数字都大于顶点处的数字的标注方法共有(种).
故选:D.
【典例2】(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【答案】D
【详解】正方体的两个顶点确定的直线有棱、面对角线、体对角线,
对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有(个);
对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个,
不存在四个顶点确定的平面与体对角线垂直,
所以正方体中“正交线面对”共有(个).
故选:D
【典例3】(2023·全国·高二课堂例题)某班班委由2位女同学、3位男同学组成,现要从该班委里选出2人去参加学校组织的培训活动,要求至少要有1位女同学参加,则不同的选法共有多少种?
【答案】7
【详解】按照选择的女同学人数分为两种情况,即2名都是女同学和只有1名女同学.
第1类:2名都是女同学的选法显然只有1种.
第2类:只有1名女同学的选法,可以分为两步完成:先从2名女同学中选出1人,有2种选法;
再从3位男同学中选出1人,有3种选法.依据分步乘法计数原理,共有不同的安排方法种.
依据分类加法计数原理,不同的选法共有种.
【变式1】(2023上·山东临沂·高二校考阶段练习)集合,,,,5,6,,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是( )
A.2 B.4 C.5 D.6
【答案】D
【详解】第二象限的横坐标是负数,纵坐标是正数.
若集合提供横坐标,集合提供纵坐标,则有,
若集合提供纵坐标,集合提供横坐标,则有,合计,
即这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数是6个,
故选:D.
【变式2】(2023下·山东菏泽·高二校考阶段练习)口袋中装有8个白球和10个红球每个球有不同编号,现从中取出2个球.
(1)至少有一个白球的取法有多少种?
(2)两球的颜色相同的取法有多少种?
【答案】(1)
(2)
【详解】(1)根据题意分2类完成任务:
第一类:白球红球各一个有种,第二类:均为白球,种,
所以共有种;
(2)根据题意分2类完成任务:
第一类:均为白球,种,第二类:均为红球,种,
所以共有种.
【变式3】(2023上·高二课时练习)从a、b、c、d、e这5个元素中取出4个,放在4个不同的格子中,且元素b不能放在第二个格子里.问:一共有多少种不同的放法?
【答案】
【详解】元素b不被取出,不同的放法有种,
当元素b被取出,则元素b有三个位置,不同的放法有种,
所以一共有种不同的放法.
题型04 用计数原理解决涂色(种植)问题
【典例1】(2023·全国·高三专题练习)现有红、黄、蓝三种颜色,对如图所示的正五角星的内部涂色(分割成六个不同区域),要求每个区域涂一种颜色且相邻部分(有公共边的两个区域)的颜色不同,则不同的涂色方法有( )
A.48种 B.64种 C.96种 D.144种
【答案】C
【详解】根据题意,假设正五角星的区域为,,,,,,如图所示,
先对区域涂色,有3种方法,再对,,,,这5个区域进行涂色,
∵,,,,这5个区域都与相邻,∴每个区域都有2种涂色方法,
∴共有种涂色方法.故选C.
【典例2】(2023下·山东·高二校联考阶段练习)如图,现要对某公园的4个区域进行绿化,有4种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,则不同的绿化方案有( )
A.48种 B.72种 C.64种 D.256种
【答案】A
【详解】从A开始摆放花卉,A有4种颜色花卉摆放方法,
C有3种颜色花卉摆放方法,B有2种颜色花卉摆放方法;
由D区与A,B花卉颜色不一样,与C区花卉颜色可以同色也可以不同色,
则D有2种颜色花卉摆放方法.
故共有种绿化方案.
故选:A
【典例3】(2023·全国·高三专题练习)用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1 2
3 4
【答案】260
【详解】第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
【变式1】(2023下·河北石家庄·高二石家庄市第四十一中学校考期中)在如图所示的四个区域中,有5种不同的花卉可选,每个区域只能种植一种花卉,且相邻区域花卉不同,则不同的种植方法共有 种(用数字作答)
【答案】240
【详解】由分步乘法计数原理得种,
故答案为:240.
【变式2】(2023·山西临汾·统考一模)如图,现要对某公园的4个区域进行绿化,有5种不同颜色的花卉可供选择,要求有公共边的两个区域不能用同一种颜色的花卉,共有 种不同的绿化方案(用数字作答).
【答案】180
【详解】如图:
A B D
C
从A开始摆放花卉,A有5种颜色花卉摆放方法,
B有4种颜色花卉摆放方法,C有3种颜色花卉摆放方法;
由D区与B,C花卉颜色不一样,与A区花卉颜色可以同色也可以不同色,
则D有3种颜色花卉摆放方法.
故共有种涂色方法.
故答案为:180
【变式3】(2023下·江苏常州·高二常州市北郊高级中学校考期中)如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同的种植方法总数为( )
A.12 B.18 C.24 D.30
【答案】B
【详解】根据题意,分3步进行分析:
(1)对于块,可以在3种不同的花中任选1种,有种情况;
(2)对于块,可以在剩下的2种不同的花中任选1种,有种情况;
(3)对于C 、D块,分2种情况:
若D块与块相同,则C块可以在其余的2种不同的花中任选1种,有种情况,
若D块与块不相同,则块有1种情况,块有1种情况,此时C 、D有1种情况,
则C 、D共有种情况;
综合可得:一共有种不同的种法.
故选:B
【变式4】(2023下·高二课时练习)用6种不同的颜色为如图所示的广告牌涂色,要求在A,B,C,D四个区域中相邻(有公共边的)区域不用同一种颜色,求共有多少种不同的涂色方法?
【答案】480(种)
【详解】方法一:分类计数,
第一类,A,D涂同色,有6×5×4=120(种)涂法,
第二类,A,D涂异色,有6×5×4×3=360(种)涂法,
共有120+360=480(种)涂法.
方法二:分步计数,先涂B区,有6种涂法,再涂C区,有5种涂法,最后涂A,D区域,各有4种涂法,
所以共有6×5×4×4=480(种)涂法.
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023上·甘肃白银·高二甘肃省靖远县第一中学校考期末)甲 乙两人从3门课程中各选修1门,则甲 乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.3种 D.9种
【答案】A
【分析】根据分步乘法计数原理求得正确答案.
【详解】甲 乙两人从3门课程中各选修1门,
由乘法原理可得甲 乙所选的课程不相同的选法有(种).
故选:A
2.(2023下·安徽池州·高二校联考期中)“声东击西”是游击战争的一种战术:声东可以击东、南、西、北中的任意一个方向,以此灵活地打击或消灭敌人.同样还有“声南击北”等不同的战术,由此可知这类战术中打击或消灭敌人的方法总数为( )
A.16 B.12 C.4 D.3
【答案】A
【分析】根据题意,分析声和击的情况,再由分步乘法计数原理可得答案.
【详解】根据题意,声的情况有4种,击的情况也有4种,所以这类战术中打击或消灭敌人的方法总数为.
故选:A.
3.(2023下·福建泉州·高二校考期末)有5名学生报名参加3项体育比赛,每人限报一项,则不同的报名方法的种数为( )
A.243 B.125 C.60 D.120
【答案】A
【分析】根据分步乘法计数原理求得正确答案.
【详解】每名学生都有种选择方法,
所以不同的报名方法的种数为.
故选:A
4.(2023下·黑龙江大庆·高二校考期中)完成一件事有三类不同方案,在第类方案中有种不同的方法,在第类方案中有种不同的方法,在第类方案中有种不同的方法,那么完成这件事共有种不同的方法,其中( )
A. B. C. D.
【答案】A
【分析】根据分类加法计数原理直接求解即可.
【详解】由分类加法计数原理得:.
故选:A.
5.(2023·全国·高三专题练习)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18 C.24 D.36
【答案】D
【分析】根据给定条件,利用分类加法计数原理列式计算作答.
【详解】正方体的两个顶点确定的直线有棱、面对角线、体对角线,
对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有(个);
对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个,
不存在四个顶点确定的平面与体对角线垂直,
所以正方体中“正交线面对”共有(个).
故选:D
6.(2023下·河北邯郸·高二校联考期中)有序数对满足,且使关于的方程有实数解,则这样的有序数对的个数为( )
A.15 B.14 C.13 D.10
【答案】A
【分析】分情况讨论即可计算有序数对的个数.
【详解】(1)当时,有为实根,则有4种可能;
(2)当时,方程有实根,所以,所以.
当时,有4种.
当时,有4种.
当时,有3种.
所以,有序数对的个数为.
故选:A.
7.(2023·全国·模拟预测)在正方形的每一个顶点处分别标上中的某一个数字(可以重复),则顶点处的数字都大于顶点处的数字的标注方法有( )
A.36种 B.48种 C.24种 D.26种
【答案】D
【分析】按顶点处标注的数字分类讨论 ,利用分类加法和乘法计数原理即可求解.
【详解】按顶点处标注的数字分类,有如下几种情况:
若处都标注的是4,则处的标注方法有(种);
若处都标注的是3,则处的标注方法有(种);
若处都标注的是2,则处的标注方法有1种;
若处标注的是4和3两个数字,则处的标注方法有(种),不同的标注方法共有(种);
若处标注的是4和2两个数字,则处的标注方法有1种,不同的标注方法共有(种);
若处标注的是3和2两个数字,则处的标注方法有1种,不同的标注方法共有(种).
由分类加法计数原理可知,顶点处的数字都大于顶点处的数字的标注方法共有(种).
故选:D.
8.(2023下·山东德州·高一统考期末)根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.算筹计数法就是用一根根同样长短和粗细的小棍子以不同的排列方式来表示数字,如图所示.如果用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹不一样多的概率为( )
A. B. C. D.
【答案】B
【分析】先求出一共摆出的两位数的个数,再求出个位和十位上的算筹不一样多的两位数的个数,利用古典概型概率公式计算即可.
【详解】用算筹随机摆出一个不含数字0的两位数,个位用纵式,十位用横式,
共可以摆出个两位数,其中个位和十位上的算筹都为1有种,
个位和十位上的算筹都为2有种,个位和十位上的算筹都为3有种,
个位和十位上的算筹都为4有种,个位和十位上的算筹都为5有种,
共有种,所以个位和十位上的算筹不一样多的有种,
所以个位和十位上的算筹不一样多的概率为.
故选:B
二、多选题
9.(2023下·广东茂名·高二统考期中)现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
【答案】ABD
【分析】利用排列知识计算得到选项ABD正确;若要选出不同颜色的2个球,有种不同的选法,所以选项C错误.
【详解】解:A. 从中任选1个球,有15种不同的选法,所以该选项正确;
B. 若每种颜色选出1个球,有120种不同的选法,所以该选项正确;
C. 若要选出不同颜色的2个球,有种不同的选法,所以该选项错误;
D. 若要不放回地依次选出2个球,有210种不同的选法,所以该选项正确.
故选:ABD
10.(2023下·山东枣庄·高二枣庄八中校考阶段练习)现有4个兴趣小组,第一、二、三、四组分别有6人、7人、8人、9人,则下列说法正确的是( )
A.选1人为负责人的选法种数为30
B.每组选1名组长的选法种数为3024
C.若推选2人发言,这2人需来自不同的小组,则不同的选法种数为335
D.若另有3名学生加入这4个小组,可自由选择小组,且第一组必有人选,则不同的选法有35种
【答案】ABC
【分析】利用加法计数原理判断选项A;利用乘法计数原理判断选项B;利用乘法及加法计数原理判断选项C;利用间接法并结合乘法计数原理判断选项D.
【详解】对于A,选1人为负责人的选法种数:,故A正确;
对于B,每组选1名组长的选法:,故B正确;
对于C,2人需来自不同的小组的选法:,故C正确;
对于D,依题意:若不考虑限制,每个人有4种选择,共有种选择,若第一组没有人选,每个人有3种选择,共有种选择,
所以不同的选法有:,故D错误;
故选:ABC.
三、填空题
11.(2023上·山东日照·高二日照一中校考阶段练习)某次足球比赛共12支球队参加,分三个阶段进行
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净胜球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
则全部赛程共需比赛 场.
【答案】
【分析】分别计算出小组赛、半决赛、决赛需要比赛场数即可得.
【详解】小组赛中每组6队进行单循环比赛,则需比赛场,
半决赛中共需场,
决赛需场,
故共需场.
故答案为:.
12.(2023下·江苏扬州·高二扬州中学校考期中)已知直线中的a,b,c是取自集合中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是 .
【答案】11
【分析】设倾斜角为,由,对分情况讨论,利用计数原理计算即可.
【详解】设倾斜角为,,则,不妨设,则,
若,a有2种取法,b有2种取法,排除1个重复(与),故这样的直线有条;
若,a有2种取法,b有2种取法,c有2种取法,且其中任两条直线均不相同,故这样的直线有条,
从而,符合要求的直线有条.
故答案为:11.
四、解答题
13.(2023上·高二课时练习)已知某容器中,H有3种同位素,Cl有2种同位素,Na有3种同位素,O有4种同位素,试问一共可以组成多少种HCl和NaOH的分子?
【答案】一共可以组成6种HCl分子,和36种NaOH的分子
【分析】根据分步计数原理求解即可.
【详解】因为HCl由H和Cl组成,且H有3种同位素,Cl有2种同位素,故可以组成种HCl.
因为NaOH由Na和OH组成,且Na有3种同位素,O有4种同位素,H有3种同位素,故OH有种情况,
故可以组成种NaOH的分子.
14.(2023·全国·高三专题练习)用6种不同颜色的彩色粉笔写黑板报,板报设计如图所示,要求相邻区域不能用同一种颜色的彩色粉笔.若允许同一种颜色多次使用,则该板报有多少种书写方案
【答案】600
【分析】根据分步相乘计数原理求解即可.
【详解】第一步,选英语角用的彩色粉笔,有6种不同的选法;
第二步,选语文学苑用的彩色粉笔,不能与英语角相同,有5种不同的选法;
第三步,选理综世界用的彩色粉笔,与英语角和语文学苑用的颜色都不相同,有4种不同的选法;
第四步,选数学天地用的彩色粉笔,只要与理综世界不同即可,有5种不同的选法.
由分步乘法计数原理知,共有种不同的书写方案.
B能力提升
1.(2023·全国·高三专题练习)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有( )
A.648个 B.720个 C.810个 D.891个
【答案】D
【分析】5位“回文数”的万位与个位相同,千位与十位相同,所以只需确定前3位即可.
【详解】根据“回文数”的特点,只需确定前3位即可,最高位即万位有9种排法,千位和百位各有10种排法,根据分步乘法计数原理,共有种排法,其中各位数字相同的共有9种,则所有5位数中是“回文数”且各位数字不全相同的共有种.
故选:D.
2.(2023下·高二单元测试)算盘是中国古代的一项重要发明.现有一种算盘(如图1),共两档,自右向左分别表示个位和十位,档中横以梁,梁上一珠拨下,记作数字,梁下五珠,上拨一珠记作数字(如图2中算盘表示整数).如果拨动图1算盘中的三枚算珠,可以表示不同整数的个数为( )
A. B. C. D.
【答案】C
【分析】分四种情况讨论:①个位拨动三枚;②十位拨动一枚,个位拨动两枚;③十位拨动两枚,个位拨动一枚;④十位拨动三枚.分别列举出每种情况下对应的数字,利用分类加法计数原理可得结果.
【详解】由题意,拨动三枚算珠,有种拨法:
①个位拨动三枚,有种结果:、;
②十位拨动一枚,个位拨动两枚,有种结果:、、、;
③十位拨动两枚,个位拨动一枚,有种结果:、、、;
④十位拨动三枚,有种结果:、.
综上,拨动题图1算盘中的三枚算珠,可以表示不同整数的个数为.
故选:C.
3.(2023下·山东枣庄·高二枣庄八中校考阶段练习)四色定理(Fourcolortheorem)又称四色猜想,是世界近代三大数学难题之一.它是于年由毕业于伦敦大学的格斯里(FrancisGuthrie)提出来的,其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”四色问题的证明进程缓慢,直到年,美国数学家运用电子计算机证明了四色定理.某校数学兴趣小组在研究给四棱锥的各个面涂颜色时,提出如下的“四色问题”:要求相邻面(含公共棱的平面)不得使用同一颜色,现有种颜色可供选择,那么不同的涂法有( )
A.种 B.种 C.种 D.种
【答案】B
【分析】先确定底面的涂色种数,然后依次确定侧面、平面的涂色方法种数,对侧面与侧面的所涂颜色是否相同进行分类讨论,确定侧面的涂色方法种数,利用分步和分类计数原理可得结果.
【详解】如下图所示:
底面的涂色有种选择,侧面有种选择,侧面有2种选择.
①若侧面与侧面所涂颜色相同,则侧面有种选择;
②若侧面与侧面所涂颜色不同,则侧面有种选择,侧面有种选择.
综上所述,不同的涂法种数为种.
故选:B.
4.(2023上·上海浦东新·高二上海师大附中校考期末)如图所示,玩具计数算盘的三档上各有7个算珠,现将每档算珠分为左右两部分,左侧的每个算珠表示数2,右侧的每个算珠表示数1(允许一侧无珠),记上、中、下三档的数字和分别为,,. 例如,图中上档的数字和. 若,,成等差数列,则不同的分珠计数法有 种.
【答案】32
【分析】先确定每档可取的整数,再根据公差分类讨论,最后根据分类计数原理得结果.
【详解】每档可取7到14中的每个整数,
若公差为0,共有8种;
若公差为±1,则共有12种;
若公差为±2,则共有8种;
若公差为±3,则共有4种;
所以,不同分珠方法有:8+12+8+4=32种,
故答案为32
【点睛】本题考查分类计数原理,考查基本分析求解能力,属难题.
5.(2023·全国·高三专题练习)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图所示.将一个正四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
【答案】420
【分析】分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解
【详解】由题设,四棱锥S - ABCD的顶点S, A, B所染的颜色互不相同,它们共有种染色方法;
当染好时,不妨设所染颜色依次为1, 2, 3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S, A, B染好时,C, D还有7种染法.
故不同的染色方法有种.
21世纪教育网(www.21cnjy.com)
