人教A版数学(选择性必修三讲义)第02讲6.2.1排列+6.2.2排列数(学生版+解析)
文档属性
| 名称 | 人教A版数学(选择性必修三讲义)第02讲6.2.1排列+6.2.2排列数(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 10:16:54 | ||
图片预览




文档简介
第02讲 6.2.1排列+6.2.2排列数
课程标准 学习目标
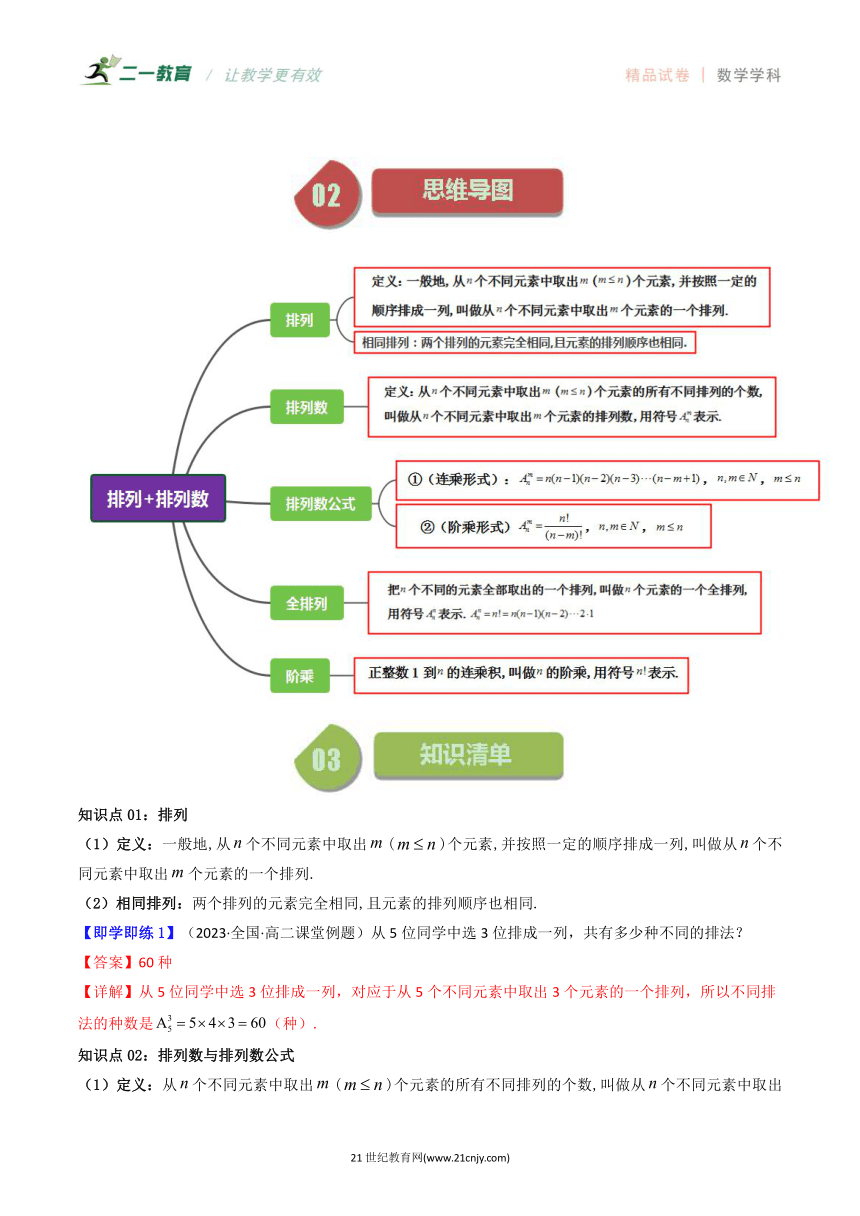
①了解排列的意义。 ②掌握常见的排列处理方法。 ③会用排列的相关方法解决简单的排列问题。 ④理解与掌握排列数公式 ⑤熟练应用排列数公式及性质求解与排列数有关的量,并能证明恒等式,求方程的解及不等式的解。 ⑥能解决一些简单的实际问题.熟练应用公式表达排列的相关关系,及求解常见的排列问题 1.通过本节课学习,要求在掌握排列的意义基础上,能解决简单的排列问题; 2能准确判断排列问题; 3.能准确用排列数公式表达排列的关系,并能应用排列数的公式求解与排列有关的实际问题与数学问题;
知识点01:排列
(1)定义:一般地,从个不同元素中取出()个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
(2)相同排列:两个排列的元素完全相同,且元素的排列顺序也相同.
【即学即练1】(2023·全国·高二课堂例题)从5位同学中选3位排成一列,共有多少种不同的排法?
【答案】60种
【详解】从5位同学中选3位排成一列,对应于从5个不同元素中取出3个元素的一个排列,所以不同排法的种数是(种).
知识点02:排列数与排列数公式
(1)定义:从个不同元素中取出()个元素的所有不同排列的个数,叫做从个不同元素中取出个元素的排列数,用符号表示.
(2)排列数公式
①(连乘形式):,,
②(阶乘形式),,
(3)全排列:把个不同的元素全部取出的一个排列,叫做个元素的一个全排列,用符号表示.
(4)阶乘:正整数1到的连乘积,叫做的阶乘,用符号表示.
【即学即练2】(2023上·高二课时练习)将6本不同的书排成一排,有多少种不同的排法?
【答案】720
【详解】将6本不同的书排成一排,一共有种不同的排法.
【即学即练3】(2021·高二课时练习)证明,并用它来化简.
【答案】证明见详解;
【详解】证明,即证.
【即学即练4】(2023·江苏·高二专题练习)解方程:.
【答案】
【详解】由题设,则,
所以,可得或,
又且,则且,
所以.
题型01 排列的定义
【典例1】1(2023下·吉林长春·高二长春外国语学校校考阶段练习)下面问题中,是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
【典例2】(2023·高二课时练习)给出下列问题:
①有10位同学,每两人互通一次电话,共通了多少次电话?
②有10位同学,每两人互写一封信,共写了多少封信?
③有10位同学,每两人互握一次手,共握了多少次手?
以上问题中,属于排列问题的是 .(写出所有满足要求的问题序号)
【典例3】(2023·高二课时练习)下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④ B.①② C.③④ D.①③④
【变式1】(2023·全国·高二专题练习)判断下列问题是否为排列问题:
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)选2个小组分别去植树和种菜;
(3)选2个小组去种菜;
(4)选10人组成一个学习小组;
(5)选3个人分别担任班长、学习委员、生活委员;
(6)某班40名学生在假期相互打电话.
【变式2】(2022·高二课时练习)下列问题是排列问题吗?
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)某班40名学生在假期相互写信;
(3)会场有50个座位,要求选出3个座位,有多少种方法?若选出3个座位安排三位客人,又有多少种方法?
(4)平面上有5个点,其中任意3个点不共线,这5个点最多可确定多少条直线?可确定多少条射线?
题型02 排列的列举问题
【典例1】(2023·高二课时练习)北京、广州、南京、天津4个城市相互通航,应该有 种机票.
【典例2】(2023上·高二课时练习)写出从a、b、c、d四个元素中任取两个不同元素的所有排列.
【典例3】(2023·高二课时练习)请列出下列排列:
(1)从4个不同元素中任取3个元素的所有排列;
(2)从7个不同元素中任取2个元素的所有排列.
【变式1】(2023·江苏·高二专题练习)从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数,能组成多少个不同的三位数?并写出这些三位数.
【变式2】(2023·江苏·高二专题练习)写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
题型03 排列数的计算、化简与证明
【典例1】(2023下·江苏苏州·高二江苏省苏州实验中学校考阶段练习)可表示为( )
A. B.
C. D.
【典例2】(多选)(2023上·河南·高二校联考阶段练习)下列等式正确的是( )
A. B.
C. D.
【典例3】(2023·江苏·高二专题练习)求不等式的解集.
【变式1】(2023下·河北张家口·高二校联考阶段练习)可表示为( )
A. B. C. D.
【变式2】(2023·江苏·高二专题练习) .
【变式3】(2023·江苏·高二专题练习)解不等式:
题型04 全排列问题
【典例1】(2023上·高二课时练习)A,B,C三名同学照相留念,成“一”字形排队,所有排列的方法种数为( )
A.3种 B.4种
C.6种 D.12种
【典例2】(2023下·江苏镇江·高二校考期末)将4名乡村振兴志愿者分配到科技助农,文艺文化,科普宣传和乡村环境治理4个项目进行培训(每个项目都有志愿者参加),每名志愿者只分配到1个项目,志愿者小王不去文艺文化项目,则不同的分配方案共有( )
A.12种 B.24种 C.18种 D.48种
【典例3】(2023·上海闵行·统考一模)今年中秋和国庆共有连续天小长假,某单位安排甲、乙、丙三名员工值班,每天都需要有人值班.任选两名员工各值天班,剩下的一名员工值天班,且每名员工值班的日期都是连续的,则不同的安排方法数为 .
【变式1】(2023下·云南曲靖·高二校考期中)若把英语单词“word”的字母顺序写错了,则可能出现的错误共有( )
A.24种 B.23种 C.12种 D.11种
【变式2】(2023下·黑龙江鸡西·高二鸡西实验中学校考期中)5月12日在鸡西实验中学报告厅开展了以“预防灾害风险,守护美好家园”为主题的消防安全知识专题讲座,还要到3个学校开讲,一个学校讲一次,不同的次序种数为( )
A.3 B. C.9 D.6
【变式3】(2023下·重庆沙坪坝·高三重庆一中校考阶段练习)8个完全相同的球放入编号1,2,3的三个空盒中,要求放入后3个盒子不空且数量均不同,则有 种放法.
题型05 元素(位置)有限制条件的排列问题
【典例1】(2023上·全国·高三专题练习)4个人排成一排,则甲不站两边的站法有( )
A.8 B.10
C.12 D.24
【典例2】(2023上·湖南邵阳·高三统考期中)某班派遣五位同学到甲,乙,丙三个街道进行打扫活动,每个街道至少有一位同学去,至多有两位同学去,且两位同学去同一个街道,则不同的派遣方法有 种.
【典例3】(2023·全国·高三专题练习)某生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案有 种.
【典例4】(2023上·陕西汉中·高二校联考阶段练习)从等7人中选5人排成一排.(以下问题的结果均用数字作答)
(1)若必须在内,有多少种排法?
(2)若都在内,且必须相邻,与都不相邻,有多少种排法?
【变式1】(2023上·江苏·高三校联考开学考试)甲、乙、丙等六人相约到电影院观看电影《封神榜》,恰好买到了六张连号的电影票.若甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为( )
A.360 B.480 C.600 D.720
【变式2】(2023上·上海浦东新·高三上海市洋泾中学校考开学考试)电视台连续播放6个广告,其中包含4个不同的商业广告和2个不同的公益广告,要求首位必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
【变式3】(2023上·高二单元测试)老师和学生共10人一起照相,其中1名老师、4名女生、5名男生,排成一行,要求男生、女生必须分性别站在一起,并且老师不站在两端,那么不同站队方式有 种.
【变式4】(2023上·高二课时练习)从7名运动员中选4名组成接力队参加4×100米接力赛.问:甲、乙两人都不跑中间两棒的排法有多少种?
题型06 相邻问题的排列问题
【典例1】(2023上·黑龙江鸡西·高三鸡西市第一中学校校考期末)2023年杭州亚运会期间,甲 乙 丙3名运动员与4名志愿者站成一排拍照留念,若甲与乙相邻 丙不排在两端,则不同的排法种数有( )
A.720 B.960 C.1120 D.1440
【典例2】(2023·山西临汾·校考模拟预测)8名同学站成两排参加文艺演出,要求两排人数相等,A不站在前排,D不站在后排,E和F左右相邻,则不同的排列方式共有( )
A.1152种 B.1728种 C.2304种 D.2880种
【典例3】(2023·广东韶关·统考一模)现有,,,,五人排成一列,其中与相邻,不排在两边,则共有 种不同的排法(用具体数字作答).
【变式1】(2023·广西·模拟预测)一排有6个插座,只有三个通电,那么恰有两个不通电的相邻的情况有( )
A.10种 B.12种 C.72种 D.144种
【变式2】(2023·江苏·统考三模)某人将斐波那契数列的前6项“1,1,2,3,5,8”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
A.120种 B.240种 C.360种 D.480种
【变式3】(2023下·重庆南岸·高二校考期中)每年5月初,高三的同学们都要拍毕业照,留下高中生活的美好见证.某班同学集体合影后有4位同学邀请两位老师合影留念.若6人站成一排,两位老师站在中间位置,甲乙两位同学站在一起,则不同的站位方法有 种.(用数字作答)
题型07 不相邻排列问题
【典例1】(2023·贵州铜仁·校联考模拟预测)2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛.现有六个参赛队伍代表站成一排照相,如果贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种.
A.144 B.72 C.36 D.24
【典例2】(2023上·湖北·高三孝感高中校联考开学考试)已知来自甲、乙、丙三个学校的5名学生参加演讲比赛,其中三个学校的学生人数分别为1、2、2.现要求相同学校的学生的演讲顺序不相邻,则不同的演讲顺序的种数为( )
A.40 B.36 C.56 D.48
【典例3】(多选)(2023下·高二单元测试)甲、乙、丙、丁四名同学和一名老师站成一排合影留念.要求老师必须站在正中间,且甲同学不与老师相邻,则不同的站法种数为( )
A. B. C. D.
【变式1】(多选)(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数可以是( )
A. B. C.84 D.
【变式2】(2023上·全国·高三专题练习),,,,五名学生按任意次序站成一排,其中和不相邻,则不同的排法种数为( )
A.72 B.36 C.18 D.64
【变式3】(2023下·海南·高二校考期中)琼中中学一条校道路边有7盏路灯,为了节约用电,学校决定每天晩上点亮其中的3盏路灯,但要求点亮的3盏路灯都不相邻,不同的点亮方式有( )种
A.5 B.10 C.15 D.20
【变式4】(2023·云南曲靖·校考三模)老师排练节目需要4个男生和2个女生,将这六名学生随机排成一排,2个女生不相邻的排法为 .
题型08 相邻(不相邻)排列综合问题
【典例1】(2023下·重庆荣昌·高二重庆市荣昌中学校校考期中)电影《长津湖》讲述了在极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神为长津湖战役胜利做出重要贡献的故事,现有4名男生和3名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【典例2】(2023下·山西晋中·高二校考期中)有甲、乙、丙、丁、戊5位同学,求:
(1)5位同学站成一排,甲、戊不在两端有多少种不同的排法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的排法?
【典例3】(2023下·江苏徐州·高二统考期中)有六位同学A,B,C,D,E,F站成一排照相,如果:
(1)A,B两人不排在一起,有几种排法?
(2)C,D两人必须排在一起,有几种排法?
(3)E不在排头,F不在排尾,有几种排法?
【变式1】(2023上·高二课时练习)4名男生、3名女生站成一排,分别求满足下列条件的站法种数.
(1)男生和女生均相邻;
(2)男生均相邻;
(3)女生均不相邻;
(4)男生与男生、女生与女生均不相邻;
(5)至少有两个女生相邻.
【变式2】(2023下·北京东城·高二景山学校校考期中)名男生和名女生(包含甲、乙)站成一排表演节目.
(1)若这名女生不能相邻,有多少种不同的排法?
(2)甲乙必须相邻,有多少种不同的排法?
(3)若甲不能站在左端,乙不能站在右端,有多少种不同的排法?
【变式3】(2023下·江苏淮安·高二校联考期中)有4名男生,3名女生,共7个人从左至右站成一排,在下列情况下,各有多少种不同的站法.
(1)男生 女生各站在一起;
(2)男生必须站在一起;
(3)男生互不相邻,且女生也互不相邻.
(4)最左端只能站某生甲或乙,最右端不能站某生甲,则有多少种不同的站法?
题型09 数字排列问题
【典例1】(2023下·上海普陀·高二校考期末)用数字、、、、组成没有重复数字的五位数,其中能被整除的数共有 个.(用数字作答)
【典例2】(2023上·高二课时练习)用可以组成多少个无重复数字的五位数?其中能被5整除的五位数有多少个?
【典例3】(2023下·广东肇庆·高二统考期末)用数字1,2,3,4,5组成没有重复数字的五位数.
(1)这个五位数为奇数,则不同的五位数有多少个?(结果用数值表示)
(2)要求3和4相邻,则不同的五位数有多少个?(结果用数值表示)
【变式1】(2023上·高二课时练习)用1,2,3,4,5,6,7这七个数字组成没有重复数字的四位数,其中偶数共有多少个?
【变式2】(2023上·高二课时练习)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
题型10 排列的综合应用
【典例1】(2023·全国·模拟预测)某中学进行数学竞赛选拔考试,,,,,共5名同学参加比赛,决出第1名到第5名的名次.和去向教练询问比赛结果,教练对说:“你和都没有得到冠军.”对说:“你不是最后一名.”从这两个回答分析,5人的名次排列方式共有( )
A.54种 B.72种 C.96种 D.120种
【典例2】(2023上·上海·高二校考阶段练习)分别求下列情形的方法数:(用数字作答)
(1)从4名男生4名女生中选出2男2女组成一个队伍;
(2)8个人排成一排,其中甲乙二人必须站在一起;
(3)8个人排成一排,甲乙丙三人互相不能相邻.
【典例3】(2023上·高二课时练习)3名男生 4名女生排成一行.在下列要求下,分别求不同排列方法的种数:
(1)甲不在最左边,乙不在最右边;
(2)男生必须排在一起;
(3)男生和女生相间排列;
(4)在甲 乙两人中间必须有3人.
【变式1】(2023·四川凉山·统考一模)五名同学彝族新年期间去邛海湿地公园采风观景,在观鸟岛湿地门口五名同学排成一排照相留念,若甲与乙相邻,丙与丁不相邻,则不同的排法共有( )
A.12种 B.24种 C.48种 D.96种
【变式2】(2023上·辽宁朝阳·高二建平县实验中学校考期末)将0,1,2,3,4这五个数字组成无重复数字的五位数,则:
(1)可以组成多少个偶数?
(2)可以组成多少个比13123大的数?
【变式3】(2023上·高二课时练习)(1)配制某种染色剂,需要加入种有机染料、种无机染料和种添加剂,其中有机染料的添加顺序不可以相邻.为研究所有不同的添加顺序对染色效果的影响,总共要试验多少次?
(2)某展览馆计划展出幅不同的画,其中水彩画幅、油画幅、国画幅.现排成一排陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端.问:有多少种不同的陈列方式?
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023下·北京通州·高二统考期中)计算:( )
A.30 B.60 C.90 D.120
2.(2023下·内蒙古乌兰察布·高二校考阶段练习)等于( )
A.107 B.323
C.320 D.348
3.(2023下·广东江门·高二校考期中)用数字1,2,3,4,5组成的无重复数字的三位数的个数为( )
A.120 B.86 C.72 D.60
4.(2023·四川乐山·统考一模)“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相同,若中间空格已填数字4,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
4
A.70 B.120 C.140 D.144
5.(2023·全国·模拟预测)甲、乙,丙、丁,戊5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,裁判说:“很遗憾,你俩都没有得到冠军.但都不是最差的.”从回答分析,5人的名次排列的不同情况可能有( )
A.27种 B.72种 C.36种 D.54种
6.(2023·河南开封·统考一模)现要从6名学生中选4名代表班级参加学校的接力赛,已知甲确定参加比赛且跑第1棒或第4棒,乙不能跑第1棒,则合适的选择方法种数为( )
A.84 B.108 C.132 D.144
7.(2023上·甘肃白银·高三甘肃省靖远县第一中学校联考阶段练习)甲 乙 丙 丁等7人站成一排,其中甲 乙相邻,丁与甲 乙 丙都不相邻的站法共有( )
A.576种 B.448种 C.288种 D.224种
8.(2023下·广西防城港·高二防城港市高级中学校考期中)用数字0、1、2、3、4、5组成没有重复数字的四位数,若将组成的不重复的四位数按从小到大的顺序排成一个数列则第85个数字为( )
A.2301 B.2304 C.2305 D.2310
二、多选题
9.(2023上·高二课时练习)(多选)用数字0,1,2,3,4,5组成没有重复数字的不同的所有四位数.下列结论正确的是( )
A. B.
C. D.-
10.(2023下·江西·高一江西师大附中校考阶段练习)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B两人站在一起有48种方法
B.若A、B不相邻共有12种方法
C.若A在B左边有60种排法
D.若A不站在最左边,B不站最右边,有72种方法
三、填空题
11.(2023上·上海长宁·高三上海市延安中学校考期中)从甲 乙等5人中任选3人参加三个不同项目的比赛,要求每个项目都有人参加,则甲 乙中至少有1人入选的不同参赛方案共有 种.
12.(2023上·广东东莞·高三校考阶段练习)某中学为庆祝建校130周年,高二年级派出甲 乙 丙 丁 戊5名老师参加“130周年办学成果展”活动,活动结束后5名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有 种(用数字作答).
四、解答题
13.(2023·全国·高二专题练习)解不等式:;
14.(2023上·陕西汉中·高二西乡县第一中学校考阶段练习)电影《志愿军雄兵出击》讲述了在极其简陋的装备和极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神取得入朝作战第一阶段战役的胜利,著名的“松骨峰战斗”在该电影中就有场景.现有3名男生和4名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
B能力提升
1.(2023·江苏南京·南京师大附中校考一模)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中a,b,c,d均为自然数,则满足条件的有序数组的个数是 .
2.(2023下·重庆沙坪坝·高二重庆一中校考阶段练习)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中均为自然数,则满足条件的有序数组的个数是 .
3.(2023上·山东德州·高二校考阶段练习)名男生和名女生站成一排.
(1)甲不在中间也不在两端的站法有多少种?
(2)甲、乙两人必须站在两端的站法有多少种?
(3)男、女分别排在一起的站法有多少种?
(4)男、女相间的站法有多少种?
(5)甲、乙、丙三人从左到右顺序一定的站法有多少种?
4.(2023·全国·高三专题练习)如图,用四种不同的颜色给三棱柱的六个顶点涂色,要求每个点涂一种颜色.
(1)若每个底面的顶点涂色所使用的颜色不相同,则不同的涂色方法共有多少种?
(2)若每条棱的两个端点涂不同的颜色,则不同的涂色方法共有多少种?
5.(2023下·江苏镇江·高二校考期中)有3名男生与4名女生,在下列不同条件下,分别求排法种数.
(1)全体排成一排,女生必须站在一起;
(2)全体排成一排,男生互不相邻;
(3)全体排成一行,其中甲,乙,丙三人从左至右的顺序不变
21世纪教育网(www.21cnjy.com)
第02讲 6.2.1排列+6.2.2排列数
课程标准 学习目标
①了解排列的意义。 ②掌握常见的排列处理方法。 ③会用排列的相关方法解决简单的排列问题。 ④理解与掌握排列数公式 ⑤熟练应用排列数公式及性质求解与排列数有关的量,并能证明恒等式,求方程的解及不等式的解。 ⑥能解决一些简单的实际问题.熟练应用公式表达排列的相关关系,及求解常见的排列问题 1.通过本节课学习,要求在掌握排列的意义基础上,能解决简单的排列问题; 2能准确判断排列问题; 3.能准确用排列数公式表达排列的关系,并能应用排列数的公式求解与排列有关的实际问题与数学问题;
知识点01:排列
(1)定义:一般地,从个不同元素中取出()个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
(2)相同排列:两个排列的元素完全相同,且元素的排列顺序也相同.
【即学即练1】(2023·全国·高二课堂例题)从5位同学中选3位排成一列,共有多少种不同的排法?
【答案】60种
【详解】从5位同学中选3位排成一列,对应于从5个不同元素中取出3个元素的一个排列,所以不同排法的种数是(种).
知识点02:排列数与排列数公式
(1)定义:从个不同元素中取出()个元素的所有不同排列的个数,叫做从个不同元素中取出个元素的排列数,用符号表示.
(2)排列数公式
①(连乘形式):,,
②(阶乘形式),,
(3)全排列:把个不同的元素全部取出的一个排列,叫做个元素的一个全排列,用符号表示.
(4)阶乘:正整数1到的连乘积,叫做的阶乘,用符号表示.
【即学即练2】(2023上·高二课时练习)将6本不同的书排成一排,有多少种不同的排法?
【答案】720
【详解】将6本不同的书排成一排,一共有种不同的排法.
【即学即练3】(2021·高二课时练习)证明,并用它来化简.
【答案】证明见详解;
【详解】证明,即证.
【即学即练4】(2023·江苏·高二专题练习)解方程:.
【答案】
【详解】由题设,则,
所以,可得或,
又且,则且,
所以.
题型01 排列的定义
【典例1】1(2023下·吉林长春·高二长春外国语学校校考阶段练习)下面问题中,是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
【答案】A
【详解】根据排列及排列数的定义,可得:
对于A中,由1,2,3三个数字组成无重复数字的三位数,符合排列的定义,是排列问题;
对于B中,从40人中选5人组成篮球队,与顺序无关的问题,不是排列问题;
对于C中, 从100人中选2人抽样调查,与顺序无关的问题,不是排列问题;
对于D中, 从1,2,3,4,5中选2个数组成集合,与顺序无关的问题,不是排列问题.
故选:A.
【典例2】(2023·高二课时练习)给出下列问题:
①有10位同学,每两人互通一次电话,共通了多少次电话?
②有10位同学,每两人互写一封信,共写了多少封信?
③有10位同学,每两人互握一次手,共握了多少次手?
以上问题中,属于排列问题的是 .(写出所有满足要求的问题序号)
【答案】②
【详解】对于①,假设10位同学中含甲乙,甲与乙通一次电话,也就是乙与甲通一次电话,没有顺序区别,故不是排列问题;
对于②,假设10位同学中含甲乙,甲给乙写一封信,跟乙给甲写一封信,是不一样的,是有顺序区别的,故属于排列问题;
对于③,假设10位同学中含甲乙,甲与乙握一次手,也就是乙与甲握一次手,没有顺序区别,故不是排列问题,
故答案为:②
【典例3】(2023·高二课时练习)下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④ B.①② C.③④ D.①③④
【答案】A
【详解】①从10个人中选2人分别去种树和扫地,与顺序有关,故是排列;②从10个人中选2人去扫地,与顺序无关,故不是排列;③从班上30名男生中选出5人组成一个篮球队,与顺序无关,故不是排列;④从数字5,6,7,8中任取两个不同的数作幂运算,与顺序有关,故是排列,故选:A.
【变式1】(2023·全国·高二专题练习)判断下列问题是否为排列问题:
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)选2个小组分别去植树和种菜;
(3)选2个小组去种菜;
(4)选10人组成一个学习小组;
(5)选3个人分别担任班长、学习委员、生活委员;
(6)某班40名学生在假期相互打电话.
【答案】(1)不是(2)是(3)不是(4)不是(5)是(6)是
【详解】(1)票价只有三种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
(2)植树和种菜是不同的,存在顺序问题,属于排列问题.
(3)不存在顺序问题,不属于排列问题.
(4)不存在顺序问题,不属于排列问题.
(5)每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
(6)A给B打电话与B给A打电话是不同的,所以存在着顺序问题,属于排列问题.
所以在上述各题中(2)(5)(6)是排列问题,(1)(3)(4)不是排列问题.
【变式2】(2022·高二课时练习)下列问题是排列问题吗?
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)某班40名学生在假期相互写信;
(3)会场有50个座位,要求选出3个座位,有多少种方法?若选出3个座位安排三位客人,又有多少种方法?
(4)平面上有5个点,其中任意3个点不共线,这5个点最多可确定多少条直线?可确定多少条射线?
【答案】(1)不是排列问题.
(2)是排列问题.
(3)选3个座位不是排列问题;选3个座位安排三位客人是排列问题.
(4)确定直线不是排列问题,确定射线是排列问题
【详解】(1)来回的票价是一样的,不存在顺序问题,所以不是排列问题.
(2)A给B写信与B给A写信是不同的两件事,所以存在着顺序,属于排列问题.
(3)任选3个座位,与顺序无关,不是排列问题;选3个座位安排三位客人,与顺序有关,故是排列问题.
(4)直线与两点的顺序无关,故确定直线不是排列问题,射线与两点的顺序有关,故确定射线是排列问题.
题型02 排列的列举问题
【典例1】(2023·高二课时练习)北京、广州、南京、天津4个城市相互通航,应该有 种机票.
【答案】12
【详解】列出每一个起点和终点情况,如图所示.
故符合题意的机票种类有:
北京→广州,北京→南京,北京→天津,广州→南京、广州→天津、广州→北京,
南京→天津,南京→北京,南京→广州,天津→北京,天津→广州,天津→南京,共12种,
故答案为:12
【典例2】(2023上·高二课时练习)写出从a、b、c、d四个元素中任取两个不同元素的所有排列.
【答案】所有的排列是ab、ac、ad、ba、bc、bd、ca、cb、cd、da、db、dc.
【详解】先画出下面的树形图:
于是可知,所有的排列是ab、ac、ad、ba、bc、bd、ca、cb、cd、da、db、dc.
【典例3】(2023·高二课时练习)请列出下列排列:
(1)从4个不同元素中任取3个元素的所有排列;
(2)从7个不同元素中任取2个元素的所有排列.
【答案】(1)答案见解析
(2)答案见解析
【详解】(1)根据题意,从4个不同元素中任取3个元素的所有排列共有如下种:
.
(2)从7个不同元素中任取2个元素的所有排列共有如下种:
.
【变式1】(2023·江苏·高二专题练习)从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数,能组成多少个不同的三位数?并写出这些三位数.
【答案】18个,答案见解析.
【详解】画出树形图,如图:
由树形图知,符合条件的三位数共有18个,
它们是102,103,120,123,130,132,201,203,210,213,230,231,301,302,310,312,320,321.
【变式2】(2023·江苏·高二专题练习)写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
【答案】(1)12;
(2)24个,答案见解析.
【详解】(1)所有两位数是12,21,13,31,14,41,23,32,24,42,34,43,共有12个不同的两位数.
(2)画出树状图,如图:
由树状图知,所有的四位数为:1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,
3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321,共24个没有重复数字的四位数.
题型03 排列数的计算、化简与证明
【典例1】(2023下·江苏苏州·高二江苏省苏州实验中学校考阶段练习)可表示为( )
A. B.
C. D.
【答案】B
【详解】
,
故选:B.
【典例2】(多选)(2023上·河南·高二校联考阶段练习)下列等式正确的是( )
A. B.
C. D.
【答案】AC
【详解】,故A正确;
由上述可知,因此,故B错误;
,故C正确;
由上述可知,故D错误.
故选:AC.
【典例3】(2023·江苏·高二专题练习)求不等式的解集.
【答案】
【详解】由题设,则,
所以,
又且,则且,
所以且,则解集为.
【变式1】(2023下·河北张家口·高二校联考阶段练习)可表示为( )
A. B. C. D.
【答案】A
【详解】中
总共有个数连乘,
故.
故选:A
【变式2】(2023·江苏·高二专题练习) .
【答案】120
【详解】由.
故答案为:
【变式3】(2023·江苏·高二专题练习)解不等式:
【答案】6
【详解】由原不等式得且,
所以,即,解得且,
所以.
题型04 全排列问题
【典例1】(2023上·高二课时练习)A,B,C三名同学照相留念,成“一”字形排队,所有排列的方法种数为( )
A.3种 B.4种
C.6种 D.12种
【答案】C
【详解】由题意所有排列的方法种数为,
故答案为:C
【典例2】(2023下·江苏镇江·高二校考期末)将4名乡村振兴志愿者分配到科技助农,文艺文化,科普宣传和乡村环境治理4个项目进行培训(每个项目都有志愿者参加),每名志愿者只分配到1个项目,志愿者小王不去文艺文化项目,则不同的分配方案共有( )
A.12种 B.24种 C.18种 D.48种
【答案】C
【详解】由题意,4名志愿者任意分配共有种分法,
若志愿者小王去文艺文化项目,其它3名任意分配有种分法,
所以志愿者小王不去文艺文化项目的分配方法有种.
故选:C
【典例3】(2023·上海闵行·统考一模)今年中秋和国庆共有连续天小长假,某单位安排甲、乙、丙三名员工值班,每天都需要有人值班.任选两名员工各值天班,剩下的一名员工值天班,且每名员工值班的日期都是连续的,则不同的安排方法数为 .
【答案】
【详解】三人值班的天数分别为、、,先确定值班天的人,有种选择,
再将三个人全排即可,所以,不同的排法种数为种.
故答案为:.
【变式1】(2023下·云南曲靖·高二校考期中)若把英语单词“word”的字母顺序写错了,则可能出现的错误共有( )
A.24种 B.23种 C.12种 D.11种
【答案】B
【详解】“word”一共有个不同的字母,
这个字母全排列有种方法,
其中正确的有种,所以错误的有种.
故选:B
【变式2】(2023下·黑龙江鸡西·高二鸡西实验中学校考期中)5月12日在鸡西实验中学报告厅开展了以“预防灾害风险,守护美好家园”为主题的消防安全知识专题讲座,还要到3个学校开讲,一个学校讲一次,不同的次序种数为( )
A.3 B. C.9 D.6
【答案】D
【详解】要到3个学校开讲,一个学校讲一次,不同的次序种数为,
故选:D.
【变式3】(2023下·重庆沙坪坝·高三重庆一中校考阶段练习)8个完全相同的球放入编号1,2,3的三个空盒中,要求放入后3个盒子不空且数量均不同,则有 种放法.
【答案】12
【详解】共两类分组方法:将8个完全相同的小球分为1,2,5三堆或1,3,4 三堆.
每类都将三堆不同个数的球放入编号1,2,3的三个空盒中,有种方法,
故共有种方法.
故答案为:12.
题型05 元素(位置)有限制条件的排列问题
【典例1】(2023上·全国·高三专题练习)4个人排成一排,则甲不站两边的站法有( )
A.8 B.10
C.12 D.24
【答案】C
【详解】甲不站两边的有种方法,
故选:C
【典例2】(2023上·湖南邵阳·高三统考期中)某班派遣五位同学到甲,乙,丙三个街道进行打扫活动,每个街道至少有一位同学去,至多有两位同学去,且两位同学去同一个街道,则不同的派遣方法有 种.
【答案】18
【详解】由题意得,学生的分配人数分别为2,2,1,
由于两位同学去同一个街道,故先从3个街道中选择1个安排,有种,
再将剩余3人分别两组,和两个街道进行全排列,有
故不同的派遣方法有种.
故答案为:18
【典例3】(2023·全国·高三专题练习)某生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案有 种.
【答案】36
【详解】由于甲、乙、丙比较特殊,因此可以将他们先安排,以他们照看第一、四道工序分类讨论.
①当甲照看第一道工序、丙照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种);
②当乙照看第一道工序、甲照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种);
③当乙照看第一道工序、丙照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种).
综上所述,不同的安排方案一共有(种).
故答案为:36.
【典例4】(2023上·陕西汉中·高二校联考阶段练习)从等7人中选5人排成一排.(以下问题的结果均用数字作答)
(1)若必须在内,有多少种排法?
(2)若都在内,且必须相邻,与都不相邻,有多少种排法?
【答案】(1)
(2)
【详解】(1)解:根据题意,若必须在内,在其余6人中选出4人,再与全排列,
共有种排法.
(2)解:根据题意,先在其他4人中选出2人,有种选法,
将看成一个整体,与选出2人全排列,有种选法,
排好后,有2个空位可用,在其中选出1个,安排,有种情况,
所以,共有种不同的排法.
【变式1】(2023上·江苏·高三校联考开学考试)甲、乙、丙等六人相约到电影院观看电影《封神榜》,恰好买到了六张连号的电影票.若甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为( )
A.360 B.480 C.600 D.720
【答案】B
【详解】由题意,甲、乙、丙等六人的全排列,共有种不同的排法,
其中甲、乙、丙三人的全排列有种不同的排法,
其中甲、乙在丙的同侧有:甲乙丙、乙甲丙、丙甲乙,丙乙甲,共4种排法,
所以甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为种.
故选:B.
【变式2】(2023上·上海浦东新·高三上海市洋泾中学校考开学考试)电视台连续播放6个广告,其中包含4个不同的商业广告和2个不同的公益广告,要求首位必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
【答案】240
【详解】因为首位必须播放公益广告,所以共有种,
故答案为:.
【变式3】(2023上·高二单元测试)老师和学生共10人一起照相,其中1名老师、4名女生、5名男生,排成一行,要求男生、女生必须分性别站在一起,并且老师不站在两端,那么不同站队方式有 种.
【答案】
【详解】要求男生、女生必须分性别站在一起,可以考虑采用捆绑法,
把男生和女生分别看成一个大元素进行处理.男生站在一起看成一个大元素,
女生站在一起看成一个大元素,老师不站在两端,共有种排列.
但4名女生、5名男生本身还有排列顺序要求.所以共有种站队方式.
故答案为:
【变式4】(2023上·高二课时练习)从7名运动员中选4名组成接力队参加4×100米接力赛.问:甲、乙两人都不跑中间两棒的排法有多少种?
【答案】400
【详解】第一步中间位置除了甲乙还有5人,5个选2个全排列跑中间两棒,有种;
第二步确定首尾的人选,还剩下5个人,选2个全排列,有种.
两步相乘,共有种.
题型06 相邻问题的排列问题
【典例1】(2023上·黑龙江鸡西·高三鸡西市第一中学校校考期末)2023年杭州亚运会期间,甲 乙 丙3名运动员与4名志愿者站成一排拍照留念,若甲与乙相邻 丙不排在两端,则不同的排法种数有( )
A.720 B.960 C.1120 D.1440
【答案】B
【详解】把甲乙捆绑成一个元素,则题设中的7个元素变为6个元素,
先排除去丙的5个元素,共有种排法,
再在中间的4个空隙中,插入丙,共有种插法,
所以甲与乙相邻 丙不排在两端,则不同的排法种数有种.
故选:B.
【典例2】(2023·山西临汾·校考模拟预测)8名同学站成两排参加文艺演出,要求两排人数相等,A不站在前排,D不站在后排,E和F左右相邻,则不同的排列方式共有( )
A.1152种 B.1728种 C.2304种 D.2880种
【答案】C
【详解】由题意可知:D站在前排,A站在后排,
若E和F站在前排,则不同的排列方式共有;
若E和F站在后排,则不同的排列方式共有;
所以不同的排列方式共有种.
故选:C.
【典例3】(2023·广东韶关·统考一模)现有,,,,五人排成一列,其中与相邻,不排在两边,则共有 种不同的排法(用具体数字作答).
【答案】24
【详解】法一:将捆绑,则除以外其他四人的排序有种,又不排在两边,
所以可选的位置有两种,所以共种排法;
法二:将捆绑,若的位置任意,则五人的排序有种,
其中排在两边的情况有种,
所以不排在两边的情况有种;
故答案为:.
【变式1】(2023·广西·模拟预测)一排有6个插座,只有三个通电,那么恰有两个不通电的相邻的情况有( )
A.10种 B.12种 C.72种 D.144种
【答案】B
【详解】三个通电的放好,有四个空,两个相邻的不通电的捆绑在一起算一个元素,
另一个不通电算一个元素,插入两个空,有顺序,所以种.
故选:B
【变式2】(2023·江苏·统考三模)某人将斐波那契数列的前6项“1,1,2,3,5,8”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
A.120种 B.240种 C.360种 D.480种
【答案】A
【详解】将两个1捆绑在一起,则可以设置的不同数字密码有种.
故选:A
【变式3】(2023下·重庆南岸·高二校考期中)每年5月初,高三的同学们都要拍毕业照,留下高中生活的美好见证.某班同学集体合影后有4位同学邀请两位老师合影留念.若6人站成一排,两位老师站在中间位置,甲乙两位同学站在一起,则不同的站位方法有 种.(用数字作答)
【答案】16
【详解】两位老师站在中间位置,有种方法,
甲乙两位同学站在两位老师的左侧或右侧,另两位同学在另一侧,有种方法,
则不同的站位方法有种.
故答案为:16.
题型07 不相邻排列问题
【典例1】(2023·贵州铜仁·校联考模拟预测)2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛.现有六个参赛队伍代表站成一排照相,如果贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种.
A.144 B.72 C.36 D.24
【答案】A
【详解】先将不相邻的两队排除,将贵阳折耳根队与柳州螺蛳粉队看成一个整体,与余下两队先排,有种方法,再将不相邻的两队插入他们的空隙中,有种方法,最后落实贵阳折耳根队与柳州螺蛳粉队的具体排法有种方法,故不同的站法有种.
故选:A.
【典例2】(2023上·湖北·高三孝感高中校联考开学考试)已知来自甲、乙、丙三个学校的5名学生参加演讲比赛,其中三个学校的学生人数分别为1、2、2.现要求相同学校的学生的演讲顺序不相邻,则不同的演讲顺序的种数为( )
A.40 B.36 C.56 D.48
【答案】D
【详解】设这5个人分别为:ABCDE,则要求B与C和D与E的演讲顺序都不能相邻.
第一类:A在BC中间,此时再把D与E插空到这3人中间,
此时的不同的演讲顺序有
第二类:A不在BC中间,此时先考虑B与C和D与E,分别将他们看成两个人的整体,再将他们的顺序应相间排列,最后考虑A,此时的不同的演讲顺序有
综上可得:总共有48种不同的演讲顺序,
故选:D.
【典例3】(多选)(2023下·高二单元测试)甲、乙、丙、丁四名同学和一名老师站成一排合影留念.要求老师必须站在正中间,且甲同学不与老师相邻,则不同的站法种数为( )
A. B. C. D.
【答案】BCD
【详解】(方法1:间接法):四名同学全排再去掉甲与老师相邻的情况为.
(方法2:直接法):特殊元素优先安排,先让老师站在正中间,甲同学从两端中任选一个位置,有种站法,其余三名学生任意排列有种排法,则不同站法共有N=N1×N2=2×6=12(种).
或者,四名同学全排时,甲同学与老师相邻与甲同学与老师不相邻各占,故有.
故选:BCD.
【变式1】(多选)(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数可以是( )
A. B. C.84 D.
【答案】AB
【详解】先除去甲、乙两人,将剩下的3人全排,共种不同的排法,
再将甲、乙两人从产生的4个空中选2个插入共种不同的排法,
所以5人并排站成一行,如果甲、乙两个人不相邻,不同的排法种数是;
5人并排站成一行有种不同的排法,
若甲、乙两个人相邻,利用捆绑法,有种不同的排法,
所以5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数是.
故选:AB.
【变式2】(2023上·全国·高三专题练习),,,,五名学生按任意次序站成一排,其中和不相邻,则不同的排法种数为( )
A.72 B.36 C.18 D.64
【答案】A
【详解】解:先将其余三人全排列,共有种情况,
再将和插空,共有种情况,
所以共有种情况,
故选:A.
【变式3】(2023下·海南·高二校考期中)琼中中学一条校道路边有7盏路灯,为了节约用电,学校决定每天晩上点亮其中的3盏路灯,但要求点亮的3盏路灯都不相邻,不同的点亮方式有( )种
A.5 B.10 C.15 D.20
【答案】B
【详解】因为不点亮的4盏灯形成5个空,将点亮的3盏灯插到这5个空中即可,
所以不同的点亮方式有种.
故选:B.
【变式4】(2023·云南曲靖·校考三模)老师排练节目需要4个男生和2个女生,将这六名学生随机排成一排,2个女生不相邻的排法为 .
【答案】
【详解】若2个女生不相邻,先排4个男生有种排法,4个男生产生5个空,
将2个女生插人5个空中有种排法,故有种排法,
故答案为:
题型08 相邻(不相邻)排列综合问题
【典例1】(2023下·重庆荣昌·高二重庆市荣昌中学校校考期中)电影《长津湖》讲述了在极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神为长津湖战役胜利做出重要贡献的故事,现有4名男生和3名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【答案】(1)720种
(2)1440种
(3)960种.
【详解】(1)根据题意,先将3个女生排在一起,有种排法,
将排好的女生视为一个整体,与4个男生进行排列,共有种排法,
由分步乘法计数原理,共有种排法;
(2)根据题意,先将4个男生排好,有种排法,
再在这4个男生之间及两头的5个空位中插入3个女生有种方法,
故符合条件的排法共有种;
(3)根据题意,先排甲、乙、丙以外的其他4人,有种排法,
由于甲、乙相邻,故再把甲、乙排好,有种排法,
最后把排好的甲、乙这个整体与丙分别插入原先排好的4人的5个空挡中有种排法,故符合条件的排法共有种.
【典例2】(2023下·山西晋中·高二校考期中)有甲、乙、丙、丁、戊5位同学,求:
(1)5位同学站成一排,甲、戊不在两端有多少种不同的排法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的排法?
【答案】(1)36;
(2)24;
【详解】(1)首先排两端,从甲、戊以外的3人中选出2人站两端,有种排法;
中间3个位置全排列,有种排法,
所以共有种排法.
(2)首先将甲乙两人捆绑,与戊一起排,有种排法,
此时,共有3个空,丙丁两人插空排列,共有种排法,
所以共有种排法.
【典例3】(2023下·江苏徐州·高二统考期中)有六位同学A,B,C,D,E,F站成一排照相,如果:
(1)A,B两人不排在一起,有几种排法?
(2)C,D两人必须排在一起,有几种排法?
(3)E不在排头,F不在排尾,有几种排法?
【答案】(1)种
(2)种
(3)种
【详解】(1)先排除A,B外的四个人,再将A,B插入到其余4人所形成的5个空中,
因此,排法种数为;
(2)将C,D两人捆绑在一起看作一个复合元素和其他4人去安排,
因此,排法种数为;
(3)E不在排头,F不在排尾,分以下两种情况讨论:
①若E在排尾,则剩下的5人全排列,故有种排法;
②若E不在排尾,则E有4个位置可选,B有4个位置可选,
将剩下的4人全排列,安排在其它4个位置即可,此时,共有种排法.
综上所述,共有种不同的排法种数.
【变式1】(2023上·高二课时练习)4名男生、3名女生站成一排,分别求满足下列条件的站法种数.
(1)男生和女生均相邻;
(2)男生均相邻;
(3)女生均不相邻;
(4)男生与男生、女生与女生均不相邻;
(5)至少有两个女生相邻.
【答案】(1)288
(2)576
(3)1440
(4)144
(5)3600
【详解】(1)因为男生和女生均相邻,将男生和女生分别看成一个整体,再进行全排,所以共有站法种数为种;
(2)因为男生均相邻,将男生看成一个整体,再和其余女生进行全排,所以共有站法种数为种;
(3)因为女生均不相邻,先将男生任意排列,再将女生插空,所以共有站法种数为种;
(4)因为男生与男生、女生与女生均不相邻,将男女生相间排列,所以共有站法种数为种;
(5)当3个女生全相邻,共有站法种数为种,
恰有2个女生相邻,共有站法种数为种,
所以至少有两个女生相邻,共有站法种数为种.
【变式2】(2023下·北京东城·高二景山学校校考期中)名男生和名女生(包含甲、乙)站成一排表演节目.
(1)若这名女生不能相邻,有多少种不同的排法?
(2)甲乙必须相邻,有多少种不同的排法?
(3)若甲不能站在左端,乙不能站在右端,有多少种不同的排法?
【答案】(1)2880
(2)10080
(3)30960
【详解】(1)要使这名女生不相邻,可以先排名男生,
再将名女生插入名男生产生的个空中,
所以这名女生不相邻的排法有种.
(2)利用捆绑法,把甲和乙捆在一起,看作一个人,
则不同的排法有种;
(3)甲站在右端,其余人全排列,有种排法.
甲不站在右端有种排法,乙有种排法,其余人全排,有种排法.
故一共有种排法.
【变式3】(2023下·江苏淮安·高二校联考期中)有4名男生,3名女生,共7个人从左至右站成一排,在下列情况下,各有多少种不同的站法.
(1)男生 女生各站在一起;
(2)男生必须站在一起;
(3)男生互不相邻,且女生也互不相邻.
(4)最左端只能站某生甲或乙,最右端不能站某生甲,则有多少种不同的站法?
【答案】(1)288
(2)576
(3)144
(4)1320
【详解】(1)男生必须站在一起,即把4名男生全排列,有种排法,
女生必须站在一起,即把3名女生全排列,有种排法,
全体男生、女生各看作一个元素全排列有种排法,
由分步乘法计数原理知共有(种)排法.
(2)把所有男生看作一个元素,与3名女生组成4个元素全排列,
故有(种)不同的排法.
(3)先排男生有种排法,
然后让女生插空,有种排法,
所以共有(种)不同的排法.
(4)若最左端站某生甲,余下6名同学全排列共有种排法;
若最左端站某生乙,
则应先排某生甲,有种排法,
剩余5名同学全排列共有种排法,
由分步计数原理知共有种排法.
根据分类加法计数原理可得,共有种.
题型09 数字排列问题
【典例1】(2023下·上海普陀·高二校考期末)用数字、、、、组成没有重复数字的五位数,其中能被整除的数共有 个.(用数字作答)
【答案】
【详解】由题意可知,个位数只能排或,其他数位没有限制,
因此,能被整除的五位数的个数为个.
故答案为:.
【典例2】(2023上·高二课时练习)用可以组成多少个无重复数字的五位数?其中能被5整除的五位数有多少个?
【答案】可以组成个无重复数字的五位数;能被5整除的五位数有个.
【详解】用可以组成个无重复数字的五位数.
若五位数的个位为,这样的五位数有个.
若五位数的个位为,这样的五位数有个.
所以其中能被5整除的五位数有个.
【典例3】(2023下·广东肇庆·高二统考期末)用数字1,2,3,4,5组成没有重复数字的五位数.
(1)这个五位数为奇数,则不同的五位数有多少个?(结果用数值表示)
(2)要求3和4相邻,则不同的五位数有多少个?(结果用数值表示)
【答案】(1)72
(2)48
【详解】(1)从1,3,5中选一个填入个位,有种,
剩余四个位置全排列,有种,
故共有个.
(2)3和4相邻,可以在第1,2位或第2,3位或第3,4位或第4,5位这4个位置中选1个,然后3和4内部全排列,有种,
其他位置进行全排列,有种,
故共有个.
【变式1】(2023上·高二课时练习)用1,2,3,4,5,6,7这七个数字组成没有重复数字的四位数,其中偶数共有多少个?
【答案】360
【详解】偶数的个位数只能是2、4、6,有种排法,其他位上有种排法,
由分步乘法计数原理,知共有四位偶数(个).
【变式2】(2023上·高二课时练习)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
【答案】36
【详解】要组成一个没有重复数字的五位数,可以分成以下步骤来完成:
第一步,排个位数,因为要求是偶数,所以只能排2或4,排法有种;
第二步,排万位数,小于50000的五位数,
万位数只能是1,3或排个位数时余下的2,4中的一个,排法有种;
在首末两位数排定后,第三步排中间3个数字时,排法有种.
根据分步乘法计数原理,所求偶数共有(个).
题型10 排列的综合应用
【典例1】(2023·全国·模拟预测)某中学进行数学竞赛选拔考试,,,,,共5名同学参加比赛,决出第1名到第5名的名次.和去向教练询问比赛结果,教练对说:“你和都没有得到冠军.”对说:“你不是最后一名.”从这两个回答分析,5人的名次排列方式共有( )
A.54种 B.72种 C.96种 D.120种
【答案】A
【详解】根据题意可知和都没有得到冠军,且不是最后一名,分两种情况:
①是最后一名,则可以为第二、三、四名,即有3种情况,剩下的三人安排在其他三个名次,
有种情况,此时有种名次排列情况;
②不是最后一名,,需要排在第二、三、四名,有种情况,剩下的三人安排在其他三个名次,有种情况,此时有种名次排列情况,则5人的名次排列方式共有种.
故选A.
【典例2】(2023上·上海·高二校考阶段练习)分别求下列情形的方法数:(用数字作答)
(1)从4名男生4名女生中选出2男2女组成一个队伍;
(2)8个人排成一排,其中甲乙二人必须站在一起;
(3)8个人排成一排,甲乙丙三人互相不能相邻.
【答案】(1)
(2)
(3)
【详解】(1)先从先从名男生中选出名,有种方法,
再从名女生中选出名,有种方法,
所以共有种方法.
(2)先把甲乙捆绑看成一个整体有种方法,再和其他人一起排列有种方法,
所以8个人排成一排,其中甲乙二人必须站在一起的方法为.
(3)先把其他人排列共有种方法,再把甲乙丙三人插空有,
所以个人排成一排,甲乙丙三人互相不能相邻的方法为.
【典例3】(2023上·高二课时练习)3名男生 4名女生排成一行.在下列要求下,分别求不同排列方法的种数:
(1)甲不在最左边,乙不在最右边;
(2)男生必须排在一起;
(3)男生和女生相间排列;
(4)在甲 乙两人中间必须有3人.
【答案】(1)
(2)
(3)
(4)
【详解】(1)依题意,先排最左边,除去甲外,有种,余下的6个位置全排有种,
但应剔除其中乙在最右边的排法数种,
则符合条件的排法共有种.
(2)将男生看成一个整体,进行全排列,有种排法,
再与其他元素进行全排列,有种排法,
故共有种.
(3)先排好男生,然后将女生插入男生所形成的四个空位,共有种.
(4)从除甲、乙以外的5人中选3人排在甲、乙中间的排法有种,
将甲、乙看作一个整体,和其余2人排成一排的排法有种,
最后再把选出的3人的排列插入到甲、乙之间即可,
共有种.
【变式1】(2023·四川凉山·统考一模)五名同学彝族新年期间去邛海湿地公园采风观景,在观鸟岛湿地门口五名同学排成一排照相留念,若甲与乙相邻,丙与丁不相邻,则不同的排法共有( )
A.12种 B.24种 C.48种 D.96种
【答案】B
【详解】甲和乙相邻,捆绑在一起有种,
再与丙和丁外的1人排列有种,
再排丙和丁有种,
故共有种排法.
故选:B.
【变式2】(2023上·辽宁朝阳·高二建平县实验中学校考期末)将0,1,2,3,4这五个数字组成无重复数字的五位数,则:
(1)可以组成多少个偶数?
(2)可以组成多少个比13123大的数?
【答案】(1)60;
(2)82.
【详解】(1)当个位数字为0时,可以组成个偶数;
当个位数字不为0时,可以组成个偶数;
所以可以组成个偶数.
(2)所组成的比13123大的五位数,可以分为以下2类:
第一类:形如,共有个,
第二类:形如,共有个,
所以可以组成个比13123大的数.
【变式3】(2023上·高二课时练习)(1)配制某种染色剂,需要加入种有机染料、种无机染料和种添加剂,其中有机染料的添加顺序不可以相邻.为研究所有不同的添加顺序对染色效果的影响,总共要试验多少次?
(2)某展览馆计划展出幅不同的画,其中水彩画幅、油画幅、国画幅.现排成一排陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端.问:有多少种不同的陈列方式?
【答案】(1);(2).
【详解】解:(1)先将种无机染料和种添加剂进行排序,
然后将种有机染料插入种无机染料和种添加剂所形成的个空位中的个,
由分步乘法计数原理可知,试验次数为;
(2)将幅油画捆绑,将幅国画捆绑,形成两个大元素,将水彩画放在“中间”,
将油画、国画放在两端,
故不同的陈列方式种数为种.
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023下·北京通州·高二统考期中)计算:( )
A.30 B.60 C.90 D.120
【答案】D
【分析】根据排列数公式计算可得结果.
【详解】.
故选:D
2.(2023下·内蒙古乌兰察布·高二校考阶段练习)等于( )
A.107 B.323
C.320 D.348
【答案】D
【分析】根据排列数计算即可;
【详解】.
故选:D.
3.(2023下·广东江门·高二校考期中)用数字1,2,3,4,5组成的无重复数字的三位数的个数为( )
A.120 B.86 C.72 D.60
【答案】D
【分析】根据排列数计算出正确答案.
【详解】依题意,组成的无重复数字的三位数的个数为.
故选:D
4.(2023·四川乐山·统考一模)“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相同,若中间空格已填数字4,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
4
A.70 B.120 C.140 D.144
【答案】B
【分析】根据排列的知识求得正确答案.
【详解】比小的有,共个,从中选出个排在的左边和上方,方法数有种,
比大的有,共个,从中选出个排在的右边和下方,方法数有种,
所以不同的填法种数为种.
故选:B
5.(2023·全国·模拟预测)甲、乙,丙、丁,戊5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,裁判说:“很遗憾,你俩都没有得到冠军.但都不是最差的.”从回答分析,5人的名次排列的不同情况可能有( )
A.27种 B.72种 C.36种 D.54种
【答案】C
【分析】根据题意,先排甲乙,再排剩下三人,由排列数的计算,即可得到结果.
【详解】根据题意,甲、乙都没有得到冠军,也都不是最后一名,
先排甲乙,再排剩下三人,则5人的名次排列种数为种.
故选:C
6.(2023·河南开封·统考一模)现要从6名学生中选4名代表班级参加学校的接力赛,已知甲确定参加比赛且跑第1棒或第4棒,乙不能跑第1棒,则合适的选择方法种数为( )
A.84 B.108 C.132 D.144
【答案】B
【分析】特殊位置优先排,分类求解可得.
【详解】当甲跑第1棒时,则有种选择方法;
当甲跑第4棒时,乙参加比赛则有种选择方法,乙不参加比赛则有种选择方法.
故合适的选择方法种数为种.
故选:B
7.(2023上·甘肃白银·高三甘肃省靖远县第一中学校联考阶段练习)甲 乙 丙 丁等7人站成一排,其中甲 乙相邻,丁与甲 乙 丙都不相邻的站法共有( )
A.576种 B.448种 C.288种 D.224种
【答案】A
【分析】分两种情况讨论,第一种情况为丙和甲 乙中的1人相邻,优先排列甲 乙 丙位置,再将三人捆绑,将除丁外三人先排列,再将捆绑的整体和丁用插空法排列即可;第二种情况为若丙和甲 乙不相邻,先优先排列甲 乙位置后捆绑,再将除甲 乙 丙、丁外的三人先排列,最后用插空法将捆绑整体和丙、丁插空排列即可.
【详解】若丙和甲 乙中的1人相邻,则满足条件的站法共有种,
若丙和甲 乙不相邻,则满足条件的站法共有种,故总的站法共有576种.
故选:A
8.(2023下·广西防城港·高二防城港市高级中学校考期中)用数字0、1、2、3、4、5组成没有重复数字的四位数,若将组成的不重复的四位数按从小到大的顺序排成一个数列则第85个数字为( )
A.2301 B.2304 C.2305 D.2310
【答案】A
【分析】依次计算首位为1、前两位为20、前两位为21的有多少个数,然后可得答案.
【详解】首位为1的有个,前两位为20的有个,前两位为21的有个,
所以第85个数字是前两位为23的最小数,即为2301.
故选:A
二、多选题
9.(2023上·高二课时练习)(多选)用数字0,1,2,3,4,5组成没有重复数字的不同的所有四位数.下列结论正确的是( )
A. B.
C. D.-
【答案】CD
【分析】可用直接法先排第一位数字,再排后三位;也可用间接法先进行全排列,再排除首位是的情况.
【详解】(直接法)先排第一位,有种方法,再排后三位有种方法,所以共有种排法;
(间接法)先进行全排列共有种排法,首位是的排法为,所以共有-排法,
故选:
10.(2023下·江西·高一江西师大附中校考阶段练习)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B两人站在一起有48种方法
B.若A、B不相邻共有12种方法
C.若A在B左边有60种排法
D.若A不站在最左边,B不站最右边,有72种方法
【答案】AC
【分析】对于A:利用捆绑法,结合排列数运算求解;对于B:利用间接法,在总体中排除A、B两人站在一起的情况;对于C:根据对称性分析求解;对于D:利用间接法,结合组合数运算求解.
【详解】对于选项A:若A、B两人站在一起,则有种方法,故A正确;
对于选项B:A、B、C、D、E五个人并排站在一起,则有种方法,
所以A、B不相邻共有种方法,故B错误;
对于选项C:根据对称可知A在B左边有种排法,故C正确;
对于选项D:A站在最左边,则有种方法,
B站最右边,则有种方法,
A站在最左边,B站最右边,则有种方法,
所以A不站在最左边,B不站最右边,有种方法,故D错误.
故选:AC
三、填空题
11.(2023上·上海长宁·高三上海市延安中学校考期中)从甲 乙等5人中任选3人参加三个不同项目的比赛,要求每个项目都有人参加,则甲 乙中至少有1人入选的不同参赛方案共有 种.
【答案】54
【分析】根据排列数利用间接法,在总体中排除没有甲、乙的参赛方案.
【详解】若甲 乙等5人中任选3人参加三个不同项目的比赛,共有种不同参赛方案,
若没有甲 乙入选的不同参赛方案共有种,
所以甲 乙中至少有1人入选的不同参赛方案共有种.
故答案为:54.
12.(2023上·广东东莞·高三校考阶段练习)某中学为庆祝建校130周年,高二年级派出甲 乙 丙 丁 戊5名老师参加“130周年办学成果展”活动,活动结束后5名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有 种(用数字作答).
【答案】24
【分析】应用捆绑、插空法,结合分步计数及排列数求不同的排法数.
【详解】将丙、丁捆绑排列有种,再把他们作为整体与戊排成一排有种,
排完后其中有3个空,最后将甲、乙插入其中的两个空有种,
综上,共有种排法.
故答案为:
四、解答题
13.(2023·全国·高二专题练习)解不等式:;
【答案】
【分析】根据排列数公式得到不等式,解得即可.
【详解】因为,,,
所以不等式可化为,
解得,又,,
所以不等式的解集为.
14.(2023上·陕西汉中·高二西乡县第一中学校考阶段练习)电影《志愿军雄兵出击》讲述了在极其简陋的装备和极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神取得入朝作战第一阶段战役的胜利,著名的“松骨峰战斗”在该电影中就有场景.现有3名男生和4名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【答案】(1)576
(2)144
(3)960
【分析】(1)由捆绑法即可得到结果;
(2)由插空法即可得到结果;
(3)结合捆绑法与插空法代入计算,即可得到结果.
【详解】(1)先将4名女生排在一起,有种排法,
将排好的女生视为一个整体,再与3名男生进行排列,共有种排法,
由分步乘法计数原理,共有种排法;
(2)先将3名男生排好,共有种排法,
在这3名男生中间以及两边的4个空位中插入4名女生,共有种排法,
再由分步乘法计数原理,共有种排法;
(3)先将甲乙丙以外的其余4人排好,共有种排法,
由于甲乙相邻,则有种排法,
最后将排好的甲乙这个整体与丙分别插入原先排好的4人的5个空隙中,
共有种排法,
由分步计数原理,共有种排法.
B能力提升
1.(2023·江苏南京·南京师大附中校考一模)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中a,b,c,d均为自然数,则满足条件的有序数组的个数是 .
【答案】28
【分析】分类讨论四个数的组成后,由计数原理求解即可.
【详解】显然a,b,c,d均为不超过5的自然数,下面进行讨论.
最大数为5的情况:
①,此时共有种情况;
最大数为4的情况:
②,此时共有种情况;
③,此时共有种情况.
当最大数为3时,,故没有满足题意的情况.
综上,满足条件的有序数组的个数是.
故答案为:28.
2.(2023下·重庆沙坪坝·高二重庆一中校考阶段练习)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中均为自然数,则满足条件的有序数组的个数是 .
【答案】29
【分析】分类讨论四个数的组成后,由计数原理求解
【详解】显然a,b,c,d均为不超过6的自然数,下面进行讨论.
最大数为6的情况:
①,此时共有种情况;
最大数为5的情况:
②,此时共有种情况;
当最大数为4时,
③,此时共有种情况;
当最大数为3时,
③,此时共有种情况;
综上,满足条件的有序数组的个数是.
故答案为:29.
3.(2023上·山东德州·高二校考阶段练习)名男生和名女生站成一排.
(1)甲不在中间也不在两端的站法有多少种?
(2)甲、乙两人必须站在两端的站法有多少种?
(3)男、女分别排在一起的站法有多少种?
(4)男、女相间的站法有多少种?
(5)甲、乙、丙三人从左到右顺序一定的站法有多少种?
【答案】(1)种
(2)种
(3)种
(4)种
(5)种
【分析】(1)按有特殊位置元素的排列方法求解;
(2)按有特殊位置元素的排列方法求解;
(3)按捆绑法排列即可;
(4)按插空法排列即可;
(5)按部分均匀的排列方法求解即可.
【详解】(1)先排甲有种,其余有种,
共有种排法.
(2)先排甲、乙,再排其余人,
共有种排法.
(3)把男生和女生分别看成一个元素,
男生和女生内部还有一个全排列,共种.
(4)先排名男生有种方法,
再将名女生插在男生形成的个空上有种方法,
故共有种排法.
(5)人共有种排法,
其中甲、乙、丙三人有种排法,
因而在种排法中每种对应一种符合条件的排法,
故共有种排法.
4.(2023·全国·高三专题练习)如图,用四种不同的颜色给三棱柱的六个顶点涂色,要求每个点涂一种颜色.
(1)若每个底面的顶点涂色所使用的颜色不相同,则不同的涂色方法共有多少种?
(2)若每条棱的两个端点涂不同的颜色,则不同的涂色方法共有多少种?
【答案】(1)576
(2)264
【详解】(1)由题得每个底面的顶点涂色所使用的颜色不相同,第一步,、、三点所涂颜色各不相同的方法有(种),第二步,、、三点所涂颜色各不相同的方法有(种),
所以由分步计数原理,不同的涂色方法共有(种).
(2)若用四种颜色,即,,,各涂一种颜色,与同色,与同色,所以有(种);
若用三种颜色,即第一类: 与同色、、各涂一种颜色,则只能涂剩余那种颜色,可以与或同色,所以有(种),
第二类:与同色、、各涂一种颜色,则只能涂剩余那种颜色,可以与或同色,所以有(种),
第三类:与同色、、各涂一种颜色,则可以涂剩余那种颜色或与同色,可以与同色或涂剩余那种颜色,所以有(种),
所以用三种颜色,有(种);
若用两种颜色,即与同色、与同色各涂一种颜色,可以涂剩余剩余两种颜色,也可以涂剩余剩余两种颜色,所以有(种).
所以由分类加法计数原理,共有(种).
5.(2023下·江苏镇江·高二校考期中)有3名男生与4名女生,在下列不同条件下,分别求排法种数.
(1)全体排成一排,女生必须站在一起;
(2)全体排成一排,男生互不相邻;
(3)全体排成一行,其中甲,乙,丙三人从左至右的顺序不变
【答案】(1)576
(2)1440
(3)840
【详解】(1)将女生看成一个整体,与名男生在一起进行全排列,有种方法,
再将名女生进行全排列,也有种方法,
故共有种排法.
(2)男生不相邻,而女生不作要求,所以应先排女生,有种方法,
再在女生之间及首尾空出的个空位中任选个空位排男生,有 种方法,
故共有种排法.
(3)从个位置中选四个安排除甲,乙,丙以外的个人,有种方法,
剩下的三个位置从左至右依次安排甲,乙,丙,仅有一种安排,
故共有种排法
21世纪教育网(www.21cnjy.com)
课程标准 学习目标
①了解排列的意义。 ②掌握常见的排列处理方法。 ③会用排列的相关方法解决简单的排列问题。 ④理解与掌握排列数公式 ⑤熟练应用排列数公式及性质求解与排列数有关的量,并能证明恒等式,求方程的解及不等式的解。 ⑥能解决一些简单的实际问题.熟练应用公式表达排列的相关关系,及求解常见的排列问题 1.通过本节课学习,要求在掌握排列的意义基础上,能解决简单的排列问题; 2能准确判断排列问题; 3.能准确用排列数公式表达排列的关系,并能应用排列数的公式求解与排列有关的实际问题与数学问题;
知识点01:排列
(1)定义:一般地,从个不同元素中取出()个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
(2)相同排列:两个排列的元素完全相同,且元素的排列顺序也相同.
【即学即练1】(2023·全国·高二课堂例题)从5位同学中选3位排成一列,共有多少种不同的排法?
【答案】60种
【详解】从5位同学中选3位排成一列,对应于从5个不同元素中取出3个元素的一个排列,所以不同排法的种数是(种).
知识点02:排列数与排列数公式
(1)定义:从个不同元素中取出()个元素的所有不同排列的个数,叫做从个不同元素中取出个元素的排列数,用符号表示.
(2)排列数公式
①(连乘形式):,,
②(阶乘形式),,
(3)全排列:把个不同的元素全部取出的一个排列,叫做个元素的一个全排列,用符号表示.
(4)阶乘:正整数1到的连乘积,叫做的阶乘,用符号表示.
【即学即练2】(2023上·高二课时练习)将6本不同的书排成一排,有多少种不同的排法?
【答案】720
【详解】将6本不同的书排成一排,一共有种不同的排法.
【即学即练3】(2021·高二课时练习)证明,并用它来化简.
【答案】证明见详解;
【详解】证明,即证.
【即学即练4】(2023·江苏·高二专题练习)解方程:.
【答案】
【详解】由题设,则,
所以,可得或,
又且,则且,
所以.
题型01 排列的定义
【典例1】1(2023下·吉林长春·高二长春外国语学校校考阶段练习)下面问题中,是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
【典例2】(2023·高二课时练习)给出下列问题:
①有10位同学,每两人互通一次电话,共通了多少次电话?
②有10位同学,每两人互写一封信,共写了多少封信?
③有10位同学,每两人互握一次手,共握了多少次手?
以上问题中,属于排列问题的是 .(写出所有满足要求的问题序号)
【典例3】(2023·高二课时练习)下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④ B.①② C.③④ D.①③④
【变式1】(2023·全国·高二专题练习)判断下列问题是否为排列问题:
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)选2个小组分别去植树和种菜;
(3)选2个小组去种菜;
(4)选10人组成一个学习小组;
(5)选3个人分别担任班长、学习委员、生活委员;
(6)某班40名学生在假期相互打电话.
【变式2】(2022·高二课时练习)下列问题是排列问题吗?
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)某班40名学生在假期相互写信;
(3)会场有50个座位,要求选出3个座位,有多少种方法?若选出3个座位安排三位客人,又有多少种方法?
(4)平面上有5个点,其中任意3个点不共线,这5个点最多可确定多少条直线?可确定多少条射线?
题型02 排列的列举问题
【典例1】(2023·高二课时练习)北京、广州、南京、天津4个城市相互通航,应该有 种机票.
【典例2】(2023上·高二课时练习)写出从a、b、c、d四个元素中任取两个不同元素的所有排列.
【典例3】(2023·高二课时练习)请列出下列排列:
(1)从4个不同元素中任取3个元素的所有排列;
(2)从7个不同元素中任取2个元素的所有排列.
【变式1】(2023·江苏·高二专题练习)从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数,能组成多少个不同的三位数?并写出这些三位数.
【变式2】(2023·江苏·高二专题练习)写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
题型03 排列数的计算、化简与证明
【典例1】(2023下·江苏苏州·高二江苏省苏州实验中学校考阶段练习)可表示为( )
A. B.
C. D.
【典例2】(多选)(2023上·河南·高二校联考阶段练习)下列等式正确的是( )
A. B.
C. D.
【典例3】(2023·江苏·高二专题练习)求不等式的解集.
【变式1】(2023下·河北张家口·高二校联考阶段练习)可表示为( )
A. B. C. D.
【变式2】(2023·江苏·高二专题练习) .
【变式3】(2023·江苏·高二专题练习)解不等式:
题型04 全排列问题
【典例1】(2023上·高二课时练习)A,B,C三名同学照相留念,成“一”字形排队,所有排列的方法种数为( )
A.3种 B.4种
C.6种 D.12种
【典例2】(2023下·江苏镇江·高二校考期末)将4名乡村振兴志愿者分配到科技助农,文艺文化,科普宣传和乡村环境治理4个项目进行培训(每个项目都有志愿者参加),每名志愿者只分配到1个项目,志愿者小王不去文艺文化项目,则不同的分配方案共有( )
A.12种 B.24种 C.18种 D.48种
【典例3】(2023·上海闵行·统考一模)今年中秋和国庆共有连续天小长假,某单位安排甲、乙、丙三名员工值班,每天都需要有人值班.任选两名员工各值天班,剩下的一名员工值天班,且每名员工值班的日期都是连续的,则不同的安排方法数为 .
【变式1】(2023下·云南曲靖·高二校考期中)若把英语单词“word”的字母顺序写错了,则可能出现的错误共有( )
A.24种 B.23种 C.12种 D.11种
【变式2】(2023下·黑龙江鸡西·高二鸡西实验中学校考期中)5月12日在鸡西实验中学报告厅开展了以“预防灾害风险,守护美好家园”为主题的消防安全知识专题讲座,还要到3个学校开讲,一个学校讲一次,不同的次序种数为( )
A.3 B. C.9 D.6
【变式3】(2023下·重庆沙坪坝·高三重庆一中校考阶段练习)8个完全相同的球放入编号1,2,3的三个空盒中,要求放入后3个盒子不空且数量均不同,则有 种放法.
题型05 元素(位置)有限制条件的排列问题
【典例1】(2023上·全国·高三专题练习)4个人排成一排,则甲不站两边的站法有( )
A.8 B.10
C.12 D.24
【典例2】(2023上·湖南邵阳·高三统考期中)某班派遣五位同学到甲,乙,丙三个街道进行打扫活动,每个街道至少有一位同学去,至多有两位同学去,且两位同学去同一个街道,则不同的派遣方法有 种.
【典例3】(2023·全国·高三专题练习)某生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案有 种.
【典例4】(2023上·陕西汉中·高二校联考阶段练习)从等7人中选5人排成一排.(以下问题的结果均用数字作答)
(1)若必须在内,有多少种排法?
(2)若都在内,且必须相邻,与都不相邻,有多少种排法?
【变式1】(2023上·江苏·高三校联考开学考试)甲、乙、丙等六人相约到电影院观看电影《封神榜》,恰好买到了六张连号的电影票.若甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为( )
A.360 B.480 C.600 D.720
【变式2】(2023上·上海浦东新·高三上海市洋泾中学校考开学考试)电视台连续播放6个广告,其中包含4个不同的商业广告和2个不同的公益广告,要求首位必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
【变式3】(2023上·高二单元测试)老师和学生共10人一起照相,其中1名老师、4名女生、5名男生,排成一行,要求男生、女生必须分性别站在一起,并且老师不站在两端,那么不同站队方式有 种.
【变式4】(2023上·高二课时练习)从7名运动员中选4名组成接力队参加4×100米接力赛.问:甲、乙两人都不跑中间两棒的排法有多少种?
题型06 相邻问题的排列问题
【典例1】(2023上·黑龙江鸡西·高三鸡西市第一中学校校考期末)2023年杭州亚运会期间,甲 乙 丙3名运动员与4名志愿者站成一排拍照留念,若甲与乙相邻 丙不排在两端,则不同的排法种数有( )
A.720 B.960 C.1120 D.1440
【典例2】(2023·山西临汾·校考模拟预测)8名同学站成两排参加文艺演出,要求两排人数相等,A不站在前排,D不站在后排,E和F左右相邻,则不同的排列方式共有( )
A.1152种 B.1728种 C.2304种 D.2880种
【典例3】(2023·广东韶关·统考一模)现有,,,,五人排成一列,其中与相邻,不排在两边,则共有 种不同的排法(用具体数字作答).
【变式1】(2023·广西·模拟预测)一排有6个插座,只有三个通电,那么恰有两个不通电的相邻的情况有( )
A.10种 B.12种 C.72种 D.144种
【变式2】(2023·江苏·统考三模)某人将斐波那契数列的前6项“1,1,2,3,5,8”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
A.120种 B.240种 C.360种 D.480种
【变式3】(2023下·重庆南岸·高二校考期中)每年5月初,高三的同学们都要拍毕业照,留下高中生活的美好见证.某班同学集体合影后有4位同学邀请两位老师合影留念.若6人站成一排,两位老师站在中间位置,甲乙两位同学站在一起,则不同的站位方法有 种.(用数字作答)
题型07 不相邻排列问题
【典例1】(2023·贵州铜仁·校联考模拟预测)2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛.现有六个参赛队伍代表站成一排照相,如果贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种.
A.144 B.72 C.36 D.24
【典例2】(2023上·湖北·高三孝感高中校联考开学考试)已知来自甲、乙、丙三个学校的5名学生参加演讲比赛,其中三个学校的学生人数分别为1、2、2.现要求相同学校的学生的演讲顺序不相邻,则不同的演讲顺序的种数为( )
A.40 B.36 C.56 D.48
【典例3】(多选)(2023下·高二单元测试)甲、乙、丙、丁四名同学和一名老师站成一排合影留念.要求老师必须站在正中间,且甲同学不与老师相邻,则不同的站法种数为( )
A. B. C. D.
【变式1】(多选)(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数可以是( )
A. B. C.84 D.
【变式2】(2023上·全国·高三专题练习),,,,五名学生按任意次序站成一排,其中和不相邻,则不同的排法种数为( )
A.72 B.36 C.18 D.64
【变式3】(2023下·海南·高二校考期中)琼中中学一条校道路边有7盏路灯,为了节约用电,学校决定每天晩上点亮其中的3盏路灯,但要求点亮的3盏路灯都不相邻,不同的点亮方式有( )种
A.5 B.10 C.15 D.20
【变式4】(2023·云南曲靖·校考三模)老师排练节目需要4个男生和2个女生,将这六名学生随机排成一排,2个女生不相邻的排法为 .
题型08 相邻(不相邻)排列综合问题
【典例1】(2023下·重庆荣昌·高二重庆市荣昌中学校校考期中)电影《长津湖》讲述了在极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神为长津湖战役胜利做出重要贡献的故事,现有4名男生和3名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【典例2】(2023下·山西晋中·高二校考期中)有甲、乙、丙、丁、戊5位同学,求:
(1)5位同学站成一排,甲、戊不在两端有多少种不同的排法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的排法?
【典例3】(2023下·江苏徐州·高二统考期中)有六位同学A,B,C,D,E,F站成一排照相,如果:
(1)A,B两人不排在一起,有几种排法?
(2)C,D两人必须排在一起,有几种排法?
(3)E不在排头,F不在排尾,有几种排法?
【变式1】(2023上·高二课时练习)4名男生、3名女生站成一排,分别求满足下列条件的站法种数.
(1)男生和女生均相邻;
(2)男生均相邻;
(3)女生均不相邻;
(4)男生与男生、女生与女生均不相邻;
(5)至少有两个女生相邻.
【变式2】(2023下·北京东城·高二景山学校校考期中)名男生和名女生(包含甲、乙)站成一排表演节目.
(1)若这名女生不能相邻,有多少种不同的排法?
(2)甲乙必须相邻,有多少种不同的排法?
(3)若甲不能站在左端,乙不能站在右端,有多少种不同的排法?
【变式3】(2023下·江苏淮安·高二校联考期中)有4名男生,3名女生,共7个人从左至右站成一排,在下列情况下,各有多少种不同的站法.
(1)男生 女生各站在一起;
(2)男生必须站在一起;
(3)男生互不相邻,且女生也互不相邻.
(4)最左端只能站某生甲或乙,最右端不能站某生甲,则有多少种不同的站法?
题型09 数字排列问题
【典例1】(2023下·上海普陀·高二校考期末)用数字、、、、组成没有重复数字的五位数,其中能被整除的数共有 个.(用数字作答)
【典例2】(2023上·高二课时练习)用可以组成多少个无重复数字的五位数?其中能被5整除的五位数有多少个?
【典例3】(2023下·广东肇庆·高二统考期末)用数字1,2,3,4,5组成没有重复数字的五位数.
(1)这个五位数为奇数,则不同的五位数有多少个?(结果用数值表示)
(2)要求3和4相邻,则不同的五位数有多少个?(结果用数值表示)
【变式1】(2023上·高二课时练习)用1,2,3,4,5,6,7这七个数字组成没有重复数字的四位数,其中偶数共有多少个?
【变式2】(2023上·高二课时练习)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
题型10 排列的综合应用
【典例1】(2023·全国·模拟预测)某中学进行数学竞赛选拔考试,,,,,共5名同学参加比赛,决出第1名到第5名的名次.和去向教练询问比赛结果,教练对说:“你和都没有得到冠军.”对说:“你不是最后一名.”从这两个回答分析,5人的名次排列方式共有( )
A.54种 B.72种 C.96种 D.120种
【典例2】(2023上·上海·高二校考阶段练习)分别求下列情形的方法数:(用数字作答)
(1)从4名男生4名女生中选出2男2女组成一个队伍;
(2)8个人排成一排,其中甲乙二人必须站在一起;
(3)8个人排成一排,甲乙丙三人互相不能相邻.
【典例3】(2023上·高二课时练习)3名男生 4名女生排成一行.在下列要求下,分别求不同排列方法的种数:
(1)甲不在最左边,乙不在最右边;
(2)男生必须排在一起;
(3)男生和女生相间排列;
(4)在甲 乙两人中间必须有3人.
【变式1】(2023·四川凉山·统考一模)五名同学彝族新年期间去邛海湿地公园采风观景,在观鸟岛湿地门口五名同学排成一排照相留念,若甲与乙相邻,丙与丁不相邻,则不同的排法共有( )
A.12种 B.24种 C.48种 D.96种
【变式2】(2023上·辽宁朝阳·高二建平县实验中学校考期末)将0,1,2,3,4这五个数字组成无重复数字的五位数,则:
(1)可以组成多少个偶数?
(2)可以组成多少个比13123大的数?
【变式3】(2023上·高二课时练习)(1)配制某种染色剂,需要加入种有机染料、种无机染料和种添加剂,其中有机染料的添加顺序不可以相邻.为研究所有不同的添加顺序对染色效果的影响,总共要试验多少次?
(2)某展览馆计划展出幅不同的画,其中水彩画幅、油画幅、国画幅.现排成一排陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端.问:有多少种不同的陈列方式?
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023下·北京通州·高二统考期中)计算:( )
A.30 B.60 C.90 D.120
2.(2023下·内蒙古乌兰察布·高二校考阶段练习)等于( )
A.107 B.323
C.320 D.348
3.(2023下·广东江门·高二校考期中)用数字1,2,3,4,5组成的无重复数字的三位数的个数为( )
A.120 B.86 C.72 D.60
4.(2023·四川乐山·统考一模)“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相同,若中间空格已填数字4,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
4
A.70 B.120 C.140 D.144
5.(2023·全国·模拟预测)甲、乙,丙、丁,戊5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,裁判说:“很遗憾,你俩都没有得到冠军.但都不是最差的.”从回答分析,5人的名次排列的不同情况可能有( )
A.27种 B.72种 C.36种 D.54种
6.(2023·河南开封·统考一模)现要从6名学生中选4名代表班级参加学校的接力赛,已知甲确定参加比赛且跑第1棒或第4棒,乙不能跑第1棒,则合适的选择方法种数为( )
A.84 B.108 C.132 D.144
7.(2023上·甘肃白银·高三甘肃省靖远县第一中学校联考阶段练习)甲 乙 丙 丁等7人站成一排,其中甲 乙相邻,丁与甲 乙 丙都不相邻的站法共有( )
A.576种 B.448种 C.288种 D.224种
8.(2023下·广西防城港·高二防城港市高级中学校考期中)用数字0、1、2、3、4、5组成没有重复数字的四位数,若将组成的不重复的四位数按从小到大的顺序排成一个数列则第85个数字为( )
A.2301 B.2304 C.2305 D.2310
二、多选题
9.(2023上·高二课时练习)(多选)用数字0,1,2,3,4,5组成没有重复数字的不同的所有四位数.下列结论正确的是( )
A. B.
C. D.-
10.(2023下·江西·高一江西师大附中校考阶段练习)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B两人站在一起有48种方法
B.若A、B不相邻共有12种方法
C.若A在B左边有60种排法
D.若A不站在最左边,B不站最右边,有72种方法
三、填空题
11.(2023上·上海长宁·高三上海市延安中学校考期中)从甲 乙等5人中任选3人参加三个不同项目的比赛,要求每个项目都有人参加,则甲 乙中至少有1人入选的不同参赛方案共有 种.
12.(2023上·广东东莞·高三校考阶段练习)某中学为庆祝建校130周年,高二年级派出甲 乙 丙 丁 戊5名老师参加“130周年办学成果展”活动,活动结束后5名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有 种(用数字作答).
四、解答题
13.(2023·全国·高二专题练习)解不等式:;
14.(2023上·陕西汉中·高二西乡县第一中学校考阶段练习)电影《志愿军雄兵出击》讲述了在极其简陋的装备和极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神取得入朝作战第一阶段战役的胜利,著名的“松骨峰战斗”在该电影中就有场景.现有3名男生和4名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
B能力提升
1.(2023·江苏南京·南京师大附中校考一模)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中a,b,c,d均为自然数,则满足条件的有序数组的个数是 .
2.(2023下·重庆沙坪坝·高二重庆一中校考阶段练习)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中均为自然数,则满足条件的有序数组的个数是 .
3.(2023上·山东德州·高二校考阶段练习)名男生和名女生站成一排.
(1)甲不在中间也不在两端的站法有多少种?
(2)甲、乙两人必须站在两端的站法有多少种?
(3)男、女分别排在一起的站法有多少种?
(4)男、女相间的站法有多少种?
(5)甲、乙、丙三人从左到右顺序一定的站法有多少种?
4.(2023·全国·高三专题练习)如图,用四种不同的颜色给三棱柱的六个顶点涂色,要求每个点涂一种颜色.
(1)若每个底面的顶点涂色所使用的颜色不相同,则不同的涂色方法共有多少种?
(2)若每条棱的两个端点涂不同的颜色,则不同的涂色方法共有多少种?
5.(2023下·江苏镇江·高二校考期中)有3名男生与4名女生,在下列不同条件下,分别求排法种数.
(1)全体排成一排,女生必须站在一起;
(2)全体排成一排,男生互不相邻;
(3)全体排成一行,其中甲,乙,丙三人从左至右的顺序不变
21世纪教育网(www.21cnjy.com)
第02讲 6.2.1排列+6.2.2排列数
课程标准 学习目标
①了解排列的意义。 ②掌握常见的排列处理方法。 ③会用排列的相关方法解决简单的排列问题。 ④理解与掌握排列数公式 ⑤熟练应用排列数公式及性质求解与排列数有关的量,并能证明恒等式,求方程的解及不等式的解。 ⑥能解决一些简单的实际问题.熟练应用公式表达排列的相关关系,及求解常见的排列问题 1.通过本节课学习,要求在掌握排列的意义基础上,能解决简单的排列问题; 2能准确判断排列问题; 3.能准确用排列数公式表达排列的关系,并能应用排列数的公式求解与排列有关的实际问题与数学问题;
知识点01:排列
(1)定义:一般地,从个不同元素中取出()个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
(2)相同排列:两个排列的元素完全相同,且元素的排列顺序也相同.
【即学即练1】(2023·全国·高二课堂例题)从5位同学中选3位排成一列,共有多少种不同的排法?
【答案】60种
【详解】从5位同学中选3位排成一列,对应于从5个不同元素中取出3个元素的一个排列,所以不同排法的种数是(种).
知识点02:排列数与排列数公式
(1)定义:从个不同元素中取出()个元素的所有不同排列的个数,叫做从个不同元素中取出个元素的排列数,用符号表示.
(2)排列数公式
①(连乘形式):,,
②(阶乘形式),,
(3)全排列:把个不同的元素全部取出的一个排列,叫做个元素的一个全排列,用符号表示.
(4)阶乘:正整数1到的连乘积,叫做的阶乘,用符号表示.
【即学即练2】(2023上·高二课时练习)将6本不同的书排成一排,有多少种不同的排法?
【答案】720
【详解】将6本不同的书排成一排,一共有种不同的排法.
【即学即练3】(2021·高二课时练习)证明,并用它来化简.
【答案】证明见详解;
【详解】证明,即证.
【即学即练4】(2023·江苏·高二专题练习)解方程:.
【答案】
【详解】由题设,则,
所以,可得或,
又且,则且,
所以.
题型01 排列的定义
【典例1】1(2023下·吉林长春·高二长春外国语学校校考阶段练习)下面问题中,是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
【答案】A
【详解】根据排列及排列数的定义,可得:
对于A中,由1,2,3三个数字组成无重复数字的三位数,符合排列的定义,是排列问题;
对于B中,从40人中选5人组成篮球队,与顺序无关的问题,不是排列问题;
对于C中, 从100人中选2人抽样调查,与顺序无关的问题,不是排列问题;
对于D中, 从1,2,3,4,5中选2个数组成集合,与顺序无关的问题,不是排列问题.
故选:A.
【典例2】(2023·高二课时练习)给出下列问题:
①有10位同学,每两人互通一次电话,共通了多少次电话?
②有10位同学,每两人互写一封信,共写了多少封信?
③有10位同学,每两人互握一次手,共握了多少次手?
以上问题中,属于排列问题的是 .(写出所有满足要求的问题序号)
【答案】②
【详解】对于①,假设10位同学中含甲乙,甲与乙通一次电话,也就是乙与甲通一次电话,没有顺序区别,故不是排列问题;
对于②,假设10位同学中含甲乙,甲给乙写一封信,跟乙给甲写一封信,是不一样的,是有顺序区别的,故属于排列问题;
对于③,假设10位同学中含甲乙,甲与乙握一次手,也就是乙与甲握一次手,没有顺序区别,故不是排列问题,
故答案为:②
【典例3】(2023·高二课时练习)下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④ B.①② C.③④ D.①③④
【答案】A
【详解】①从10个人中选2人分别去种树和扫地,与顺序有关,故是排列;②从10个人中选2人去扫地,与顺序无关,故不是排列;③从班上30名男生中选出5人组成一个篮球队,与顺序无关,故不是排列;④从数字5,6,7,8中任取两个不同的数作幂运算,与顺序有关,故是排列,故选:A.
【变式1】(2023·全国·高二专题练习)判断下列问题是否为排列问题:
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)选2个小组分别去植树和种菜;
(3)选2个小组去种菜;
(4)选10人组成一个学习小组;
(5)选3个人分别担任班长、学习委员、生活委员;
(6)某班40名学生在假期相互打电话.
【答案】(1)不是(2)是(3)不是(4)不是(5)是(6)是
【详解】(1)票价只有三种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
(2)植树和种菜是不同的,存在顺序问题,属于排列问题.
(3)不存在顺序问题,不属于排列问题.
(4)不存在顺序问题,不属于排列问题.
(5)每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
(6)A给B打电话与B给A打电话是不同的,所以存在着顺序问题,属于排列问题.
所以在上述各题中(2)(5)(6)是排列问题,(1)(3)(4)不是排列问题.
【变式2】(2022·高二课时练习)下列问题是排列问题吗?
(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);
(2)某班40名学生在假期相互写信;
(3)会场有50个座位,要求选出3个座位,有多少种方法?若选出3个座位安排三位客人,又有多少种方法?
(4)平面上有5个点,其中任意3个点不共线,这5个点最多可确定多少条直线?可确定多少条射线?
【答案】(1)不是排列问题.
(2)是排列问题.
(3)选3个座位不是排列问题;选3个座位安排三位客人是排列问题.
(4)确定直线不是排列问题,确定射线是排列问题
【详解】(1)来回的票价是一样的,不存在顺序问题,所以不是排列问题.
(2)A给B写信与B给A写信是不同的两件事,所以存在着顺序,属于排列问题.
(3)任选3个座位,与顺序无关,不是排列问题;选3个座位安排三位客人,与顺序有关,故是排列问题.
(4)直线与两点的顺序无关,故确定直线不是排列问题,射线与两点的顺序有关,故确定射线是排列问题.
题型02 排列的列举问题
【典例1】(2023·高二课时练习)北京、广州、南京、天津4个城市相互通航,应该有 种机票.
【答案】12
【详解】列出每一个起点和终点情况,如图所示.
故符合题意的机票种类有:
北京→广州,北京→南京,北京→天津,广州→南京、广州→天津、广州→北京,
南京→天津,南京→北京,南京→广州,天津→北京,天津→广州,天津→南京,共12种,
故答案为:12
【典例2】(2023上·高二课时练习)写出从a、b、c、d四个元素中任取两个不同元素的所有排列.
【答案】所有的排列是ab、ac、ad、ba、bc、bd、ca、cb、cd、da、db、dc.
【详解】先画出下面的树形图:
于是可知,所有的排列是ab、ac、ad、ba、bc、bd、ca、cb、cd、da、db、dc.
【典例3】(2023·高二课时练习)请列出下列排列:
(1)从4个不同元素中任取3个元素的所有排列;
(2)从7个不同元素中任取2个元素的所有排列.
【答案】(1)答案见解析
(2)答案见解析
【详解】(1)根据题意,从4个不同元素中任取3个元素的所有排列共有如下种:
.
(2)从7个不同元素中任取2个元素的所有排列共有如下种:
.
【变式1】(2023·江苏·高二专题练习)从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数,能组成多少个不同的三位数?并写出这些三位数.
【答案】18个,答案见解析.
【详解】画出树形图,如图:
由树形图知,符合条件的三位数共有18个,
它们是102,103,120,123,130,132,201,203,210,213,230,231,301,302,310,312,320,321.
【变式2】(2023·江苏·高二专题练习)写出下列问题的所有排列:
(1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)由1,2,3,4四个数字能组成多少个没有重复数字的四位数?试全部列出.
【答案】(1)12;
(2)24个,答案见解析.
【详解】(1)所有两位数是12,21,13,31,14,41,23,32,24,42,34,43,共有12个不同的两位数.
(2)画出树状图,如图:
由树状图知,所有的四位数为:1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,
3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321,共24个没有重复数字的四位数.
题型03 排列数的计算、化简与证明
【典例1】(2023下·江苏苏州·高二江苏省苏州实验中学校考阶段练习)可表示为( )
A. B.
C. D.
【答案】B
【详解】
,
故选:B.
【典例2】(多选)(2023上·河南·高二校联考阶段练习)下列等式正确的是( )
A. B.
C. D.
【答案】AC
【详解】,故A正确;
由上述可知,因此,故B错误;
,故C正确;
由上述可知,故D错误.
故选:AC.
【典例3】(2023·江苏·高二专题练习)求不等式的解集.
【答案】
【详解】由题设,则,
所以,
又且,则且,
所以且,则解集为.
【变式1】(2023下·河北张家口·高二校联考阶段练习)可表示为( )
A. B. C. D.
【答案】A
【详解】中
总共有个数连乘,
故.
故选:A
【变式2】(2023·江苏·高二专题练习) .
【答案】120
【详解】由.
故答案为:
【变式3】(2023·江苏·高二专题练习)解不等式:
【答案】6
【详解】由原不等式得且,
所以,即,解得且,
所以.
题型04 全排列问题
【典例1】(2023上·高二课时练习)A,B,C三名同学照相留念,成“一”字形排队,所有排列的方法种数为( )
A.3种 B.4种
C.6种 D.12种
【答案】C
【详解】由题意所有排列的方法种数为,
故答案为:C
【典例2】(2023下·江苏镇江·高二校考期末)将4名乡村振兴志愿者分配到科技助农,文艺文化,科普宣传和乡村环境治理4个项目进行培训(每个项目都有志愿者参加),每名志愿者只分配到1个项目,志愿者小王不去文艺文化项目,则不同的分配方案共有( )
A.12种 B.24种 C.18种 D.48种
【答案】C
【详解】由题意,4名志愿者任意分配共有种分法,
若志愿者小王去文艺文化项目,其它3名任意分配有种分法,
所以志愿者小王不去文艺文化项目的分配方法有种.
故选:C
【典例3】(2023·上海闵行·统考一模)今年中秋和国庆共有连续天小长假,某单位安排甲、乙、丙三名员工值班,每天都需要有人值班.任选两名员工各值天班,剩下的一名员工值天班,且每名员工值班的日期都是连续的,则不同的安排方法数为 .
【答案】
【详解】三人值班的天数分别为、、,先确定值班天的人,有种选择,
再将三个人全排即可,所以,不同的排法种数为种.
故答案为:.
【变式1】(2023下·云南曲靖·高二校考期中)若把英语单词“word”的字母顺序写错了,则可能出现的错误共有( )
A.24种 B.23种 C.12种 D.11种
【答案】B
【详解】“word”一共有个不同的字母,
这个字母全排列有种方法,
其中正确的有种,所以错误的有种.
故选:B
【变式2】(2023下·黑龙江鸡西·高二鸡西实验中学校考期中)5月12日在鸡西实验中学报告厅开展了以“预防灾害风险,守护美好家园”为主题的消防安全知识专题讲座,还要到3个学校开讲,一个学校讲一次,不同的次序种数为( )
A.3 B. C.9 D.6
【答案】D
【详解】要到3个学校开讲,一个学校讲一次,不同的次序种数为,
故选:D.
【变式3】(2023下·重庆沙坪坝·高三重庆一中校考阶段练习)8个完全相同的球放入编号1,2,3的三个空盒中,要求放入后3个盒子不空且数量均不同,则有 种放法.
【答案】12
【详解】共两类分组方法:将8个完全相同的小球分为1,2,5三堆或1,3,4 三堆.
每类都将三堆不同个数的球放入编号1,2,3的三个空盒中,有种方法,
故共有种方法.
故答案为:12.
题型05 元素(位置)有限制条件的排列问题
【典例1】(2023上·全国·高三专题练习)4个人排成一排,则甲不站两边的站法有( )
A.8 B.10
C.12 D.24
【答案】C
【详解】甲不站两边的有种方法,
故选:C
【典例2】(2023上·湖南邵阳·高三统考期中)某班派遣五位同学到甲,乙,丙三个街道进行打扫活动,每个街道至少有一位同学去,至多有两位同学去,且两位同学去同一个街道,则不同的派遣方法有 种.
【答案】18
【详解】由题意得,学生的分配人数分别为2,2,1,
由于两位同学去同一个街道,故先从3个街道中选择1个安排,有种,
再将剩余3人分别两组,和两个街道进行全排列,有
故不同的派遣方法有种.
故答案为:18
【典例3】(2023·全国·高三专题练习)某生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案有 种.
【答案】36
【详解】由于甲、乙、丙比较特殊,因此可以将他们先安排,以他们照看第一、四道工序分类讨论.
①当甲照看第一道工序、丙照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种);
②当乙照看第一道工序、甲照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种);
③当乙照看第一道工序、丙照看第四道工序时,剩下4个人选择2个照看中间两道工序,于是有(种).
综上所述,不同的安排方案一共有(种).
故答案为:36.
【典例4】(2023上·陕西汉中·高二校联考阶段练习)从等7人中选5人排成一排.(以下问题的结果均用数字作答)
(1)若必须在内,有多少种排法?
(2)若都在内,且必须相邻,与都不相邻,有多少种排法?
【答案】(1)
(2)
【详解】(1)解:根据题意,若必须在内,在其余6人中选出4人,再与全排列,
共有种排法.
(2)解:根据题意,先在其他4人中选出2人,有种选法,
将看成一个整体,与选出2人全排列,有种选法,
排好后,有2个空位可用,在其中选出1个,安排,有种情况,
所以,共有种不同的排法.
【变式1】(2023上·江苏·高三校联考开学考试)甲、乙、丙等六人相约到电影院观看电影《封神榜》,恰好买到了六张连号的电影票.若甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为( )
A.360 B.480 C.600 D.720
【答案】B
【详解】由题意,甲、乙、丙等六人的全排列,共有种不同的排法,
其中甲、乙、丙三人的全排列有种不同的排法,
其中甲、乙在丙的同侧有:甲乙丙、乙甲丙、丙甲乙,丙乙甲,共4种排法,
所以甲、乙两人必须坐在丙的同一侧,则不同的坐法种数为种.
故选:B.
【变式2】(2023上·上海浦东新·高三上海市洋泾中学校考开学考试)电视台连续播放6个广告,其中包含4个不同的商业广告和2个不同的公益广告,要求首位必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
【答案】240
【详解】因为首位必须播放公益广告,所以共有种,
故答案为:.
【变式3】(2023上·高二单元测试)老师和学生共10人一起照相,其中1名老师、4名女生、5名男生,排成一行,要求男生、女生必须分性别站在一起,并且老师不站在两端,那么不同站队方式有 种.
【答案】
【详解】要求男生、女生必须分性别站在一起,可以考虑采用捆绑法,
把男生和女生分别看成一个大元素进行处理.男生站在一起看成一个大元素,
女生站在一起看成一个大元素,老师不站在两端,共有种排列.
但4名女生、5名男生本身还有排列顺序要求.所以共有种站队方式.
故答案为:
【变式4】(2023上·高二课时练习)从7名运动员中选4名组成接力队参加4×100米接力赛.问:甲、乙两人都不跑中间两棒的排法有多少种?
【答案】400
【详解】第一步中间位置除了甲乙还有5人,5个选2个全排列跑中间两棒,有种;
第二步确定首尾的人选,还剩下5个人,选2个全排列,有种.
两步相乘,共有种.
题型06 相邻问题的排列问题
【典例1】(2023上·黑龙江鸡西·高三鸡西市第一中学校校考期末)2023年杭州亚运会期间,甲 乙 丙3名运动员与4名志愿者站成一排拍照留念,若甲与乙相邻 丙不排在两端,则不同的排法种数有( )
A.720 B.960 C.1120 D.1440
【答案】B
【详解】把甲乙捆绑成一个元素,则题设中的7个元素变为6个元素,
先排除去丙的5个元素,共有种排法,
再在中间的4个空隙中,插入丙,共有种插法,
所以甲与乙相邻 丙不排在两端,则不同的排法种数有种.
故选:B.
【典例2】(2023·山西临汾·校考模拟预测)8名同学站成两排参加文艺演出,要求两排人数相等,A不站在前排,D不站在后排,E和F左右相邻,则不同的排列方式共有( )
A.1152种 B.1728种 C.2304种 D.2880种
【答案】C
【详解】由题意可知:D站在前排,A站在后排,
若E和F站在前排,则不同的排列方式共有;
若E和F站在后排,则不同的排列方式共有;
所以不同的排列方式共有种.
故选:C.
【典例3】(2023·广东韶关·统考一模)现有,,,,五人排成一列,其中与相邻,不排在两边,则共有 种不同的排法(用具体数字作答).
【答案】24
【详解】法一:将捆绑,则除以外其他四人的排序有种,又不排在两边,
所以可选的位置有两种,所以共种排法;
法二:将捆绑,若的位置任意,则五人的排序有种,
其中排在两边的情况有种,
所以不排在两边的情况有种;
故答案为:.
【变式1】(2023·广西·模拟预测)一排有6个插座,只有三个通电,那么恰有两个不通电的相邻的情况有( )
A.10种 B.12种 C.72种 D.144种
【答案】B
【详解】三个通电的放好,有四个空,两个相邻的不通电的捆绑在一起算一个元素,
另一个不通电算一个元素,插入两个空,有顺序,所以种.
故选:B
【变式2】(2023·江苏·统考三模)某人将斐波那契数列的前6项“1,1,2,3,5,8”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
A.120种 B.240种 C.360种 D.480种
【答案】A
【详解】将两个1捆绑在一起,则可以设置的不同数字密码有种.
故选:A
【变式3】(2023下·重庆南岸·高二校考期中)每年5月初,高三的同学们都要拍毕业照,留下高中生活的美好见证.某班同学集体合影后有4位同学邀请两位老师合影留念.若6人站成一排,两位老师站在中间位置,甲乙两位同学站在一起,则不同的站位方法有 种.(用数字作答)
【答案】16
【详解】两位老师站在中间位置,有种方法,
甲乙两位同学站在两位老师的左侧或右侧,另两位同学在另一侧,有种方法,
则不同的站位方法有种.
故答案为:16.
题型07 不相邻排列问题
【典例1】(2023·贵州铜仁·校联考模拟预测)2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛.现有六个参赛队伍代表站成一排照相,如果贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种.
A.144 B.72 C.36 D.24
【答案】A
【详解】先将不相邻的两队排除,将贵阳折耳根队与柳州螺蛳粉队看成一个整体,与余下两队先排,有种方法,再将不相邻的两队插入他们的空隙中,有种方法,最后落实贵阳折耳根队与柳州螺蛳粉队的具体排法有种方法,故不同的站法有种.
故选:A.
【典例2】(2023上·湖北·高三孝感高中校联考开学考试)已知来自甲、乙、丙三个学校的5名学生参加演讲比赛,其中三个学校的学生人数分别为1、2、2.现要求相同学校的学生的演讲顺序不相邻,则不同的演讲顺序的种数为( )
A.40 B.36 C.56 D.48
【答案】D
【详解】设这5个人分别为:ABCDE,则要求B与C和D与E的演讲顺序都不能相邻.
第一类:A在BC中间,此时再把D与E插空到这3人中间,
此时的不同的演讲顺序有
第二类:A不在BC中间,此时先考虑B与C和D与E,分别将他们看成两个人的整体,再将他们的顺序应相间排列,最后考虑A,此时的不同的演讲顺序有
综上可得:总共有48种不同的演讲顺序,
故选:D.
【典例3】(多选)(2023下·高二单元测试)甲、乙、丙、丁四名同学和一名老师站成一排合影留念.要求老师必须站在正中间,且甲同学不与老师相邻,则不同的站法种数为( )
A. B. C. D.
【答案】BCD
【详解】(方法1:间接法):四名同学全排再去掉甲与老师相邻的情况为.
(方法2:直接法):特殊元素优先安排,先让老师站在正中间,甲同学从两端中任选一个位置,有种站法,其余三名学生任意排列有种排法,则不同站法共有N=N1×N2=2×6=12(种).
或者,四名同学全排时,甲同学与老师相邻与甲同学与老师不相邻各占,故有.
故选:BCD.
【变式1】(多选)(2023下·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期中)5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数可以是( )
A. B. C.84 D.
【答案】AB
【详解】先除去甲、乙两人,将剩下的3人全排,共种不同的排法,
再将甲、乙两人从产生的4个空中选2个插入共种不同的排法,
所以5人并排站成一行,如果甲、乙两个人不相邻,不同的排法种数是;
5人并排站成一行有种不同的排法,
若甲、乙两个人相邻,利用捆绑法,有种不同的排法,
所以5人并排站成一行,如果甲、乙两个人不相邻,那么不同的排法种数是.
故选:AB.
【变式2】(2023上·全国·高三专题练习),,,,五名学生按任意次序站成一排,其中和不相邻,则不同的排法种数为( )
A.72 B.36 C.18 D.64
【答案】A
【详解】解:先将其余三人全排列,共有种情况,
再将和插空,共有种情况,
所以共有种情况,
故选:A.
【变式3】(2023下·海南·高二校考期中)琼中中学一条校道路边有7盏路灯,为了节约用电,学校决定每天晩上点亮其中的3盏路灯,但要求点亮的3盏路灯都不相邻,不同的点亮方式有( )种
A.5 B.10 C.15 D.20
【答案】B
【详解】因为不点亮的4盏灯形成5个空,将点亮的3盏灯插到这5个空中即可,
所以不同的点亮方式有种.
故选:B.
【变式4】(2023·云南曲靖·校考三模)老师排练节目需要4个男生和2个女生,将这六名学生随机排成一排,2个女生不相邻的排法为 .
【答案】
【详解】若2个女生不相邻,先排4个男生有种排法,4个男生产生5个空,
将2个女生插人5个空中有种排法,故有种排法,
故答案为:
题型08 相邻(不相邻)排列综合问题
【典例1】(2023下·重庆荣昌·高二重庆市荣昌中学校校考期中)电影《长津湖》讲述了在极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神为长津湖战役胜利做出重要贡献的故事,现有4名男生和3名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【答案】(1)720种
(2)1440种
(3)960种.
【详解】(1)根据题意,先将3个女生排在一起,有种排法,
将排好的女生视为一个整体,与4个男生进行排列,共有种排法,
由分步乘法计数原理,共有种排法;
(2)根据题意,先将4个男生排好,有种排法,
再在这4个男生之间及两头的5个空位中插入3个女生有种方法,
故符合条件的排法共有种;
(3)根据题意,先排甲、乙、丙以外的其他4人,有种排法,
由于甲、乙相邻,故再把甲、乙排好,有种排法,
最后把排好的甲、乙这个整体与丙分别插入原先排好的4人的5个空挡中有种排法,故符合条件的排法共有种.
【典例2】(2023下·山西晋中·高二校考期中)有甲、乙、丙、丁、戊5位同学,求:
(1)5位同学站成一排,甲、戊不在两端有多少种不同的排法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的排法?
【答案】(1)36;
(2)24;
【详解】(1)首先排两端,从甲、戊以外的3人中选出2人站两端,有种排法;
中间3个位置全排列,有种排法,
所以共有种排法.
(2)首先将甲乙两人捆绑,与戊一起排,有种排法,
此时,共有3个空,丙丁两人插空排列,共有种排法,
所以共有种排法.
【典例3】(2023下·江苏徐州·高二统考期中)有六位同学A,B,C,D,E,F站成一排照相,如果:
(1)A,B两人不排在一起,有几种排法?
(2)C,D两人必须排在一起,有几种排法?
(3)E不在排头,F不在排尾,有几种排法?
【答案】(1)种
(2)种
(3)种
【详解】(1)先排除A,B外的四个人,再将A,B插入到其余4人所形成的5个空中,
因此,排法种数为;
(2)将C,D两人捆绑在一起看作一个复合元素和其他4人去安排,
因此,排法种数为;
(3)E不在排头,F不在排尾,分以下两种情况讨论:
①若E在排尾,则剩下的5人全排列,故有种排法;
②若E不在排尾,则E有4个位置可选,B有4个位置可选,
将剩下的4人全排列,安排在其它4个位置即可,此时,共有种排法.
综上所述,共有种不同的排法种数.
【变式1】(2023上·高二课时练习)4名男生、3名女生站成一排,分别求满足下列条件的站法种数.
(1)男生和女生均相邻;
(2)男生均相邻;
(3)女生均不相邻;
(4)男生与男生、女生与女生均不相邻;
(5)至少有两个女生相邻.
【答案】(1)288
(2)576
(3)1440
(4)144
(5)3600
【详解】(1)因为男生和女生均相邻,将男生和女生分别看成一个整体,再进行全排,所以共有站法种数为种;
(2)因为男生均相邻,将男生看成一个整体,再和其余女生进行全排,所以共有站法种数为种;
(3)因为女生均不相邻,先将男生任意排列,再将女生插空,所以共有站法种数为种;
(4)因为男生与男生、女生与女生均不相邻,将男女生相间排列,所以共有站法种数为种;
(5)当3个女生全相邻,共有站法种数为种,
恰有2个女生相邻,共有站法种数为种,
所以至少有两个女生相邻,共有站法种数为种.
【变式2】(2023下·北京东城·高二景山学校校考期中)名男生和名女生(包含甲、乙)站成一排表演节目.
(1)若这名女生不能相邻,有多少种不同的排法?
(2)甲乙必须相邻,有多少种不同的排法?
(3)若甲不能站在左端,乙不能站在右端,有多少种不同的排法?
【答案】(1)2880
(2)10080
(3)30960
【详解】(1)要使这名女生不相邻,可以先排名男生,
再将名女生插入名男生产生的个空中,
所以这名女生不相邻的排法有种.
(2)利用捆绑法,把甲和乙捆在一起,看作一个人,
则不同的排法有种;
(3)甲站在右端,其余人全排列,有种排法.
甲不站在右端有种排法,乙有种排法,其余人全排,有种排法.
故一共有种排法.
【变式3】(2023下·江苏淮安·高二校联考期中)有4名男生,3名女生,共7个人从左至右站成一排,在下列情况下,各有多少种不同的站法.
(1)男生 女生各站在一起;
(2)男生必须站在一起;
(3)男生互不相邻,且女生也互不相邻.
(4)最左端只能站某生甲或乙,最右端不能站某生甲,则有多少种不同的站法?
【答案】(1)288
(2)576
(3)144
(4)1320
【详解】(1)男生必须站在一起,即把4名男生全排列,有种排法,
女生必须站在一起,即把3名女生全排列,有种排法,
全体男生、女生各看作一个元素全排列有种排法,
由分步乘法计数原理知共有(种)排法.
(2)把所有男生看作一个元素,与3名女生组成4个元素全排列,
故有(种)不同的排法.
(3)先排男生有种排法,
然后让女生插空,有种排法,
所以共有(种)不同的排法.
(4)若最左端站某生甲,余下6名同学全排列共有种排法;
若最左端站某生乙,
则应先排某生甲,有种排法,
剩余5名同学全排列共有种排法,
由分步计数原理知共有种排法.
根据分类加法计数原理可得,共有种.
题型09 数字排列问题
【典例1】(2023下·上海普陀·高二校考期末)用数字、、、、组成没有重复数字的五位数,其中能被整除的数共有 个.(用数字作答)
【答案】
【详解】由题意可知,个位数只能排或,其他数位没有限制,
因此,能被整除的五位数的个数为个.
故答案为:.
【典例2】(2023上·高二课时练习)用可以组成多少个无重复数字的五位数?其中能被5整除的五位数有多少个?
【答案】可以组成个无重复数字的五位数;能被5整除的五位数有个.
【详解】用可以组成个无重复数字的五位数.
若五位数的个位为,这样的五位数有个.
若五位数的个位为,这样的五位数有个.
所以其中能被5整除的五位数有个.
【典例3】(2023下·广东肇庆·高二统考期末)用数字1,2,3,4,5组成没有重复数字的五位数.
(1)这个五位数为奇数,则不同的五位数有多少个?(结果用数值表示)
(2)要求3和4相邻,则不同的五位数有多少个?(结果用数值表示)
【答案】(1)72
(2)48
【详解】(1)从1,3,5中选一个填入个位,有种,
剩余四个位置全排列,有种,
故共有个.
(2)3和4相邻,可以在第1,2位或第2,3位或第3,4位或第4,5位这4个位置中选1个,然后3和4内部全排列,有种,
其他位置进行全排列,有种,
故共有个.
【变式1】(2023上·高二课时练习)用1,2,3,4,5,6,7这七个数字组成没有重复数字的四位数,其中偶数共有多少个?
【答案】360
【详解】偶数的个位数只能是2、4、6,有种排法,其他位上有种排法,
由分步乘法计数原理,知共有四位偶数(个).
【变式2】(2023上·高二课时练习)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
【答案】36
【详解】要组成一个没有重复数字的五位数,可以分成以下步骤来完成:
第一步,排个位数,因为要求是偶数,所以只能排2或4,排法有种;
第二步,排万位数,小于50000的五位数,
万位数只能是1,3或排个位数时余下的2,4中的一个,排法有种;
在首末两位数排定后,第三步排中间3个数字时,排法有种.
根据分步乘法计数原理,所求偶数共有(个).
题型10 排列的综合应用
【典例1】(2023·全国·模拟预测)某中学进行数学竞赛选拔考试,,,,,共5名同学参加比赛,决出第1名到第5名的名次.和去向教练询问比赛结果,教练对说:“你和都没有得到冠军.”对说:“你不是最后一名.”从这两个回答分析,5人的名次排列方式共有( )
A.54种 B.72种 C.96种 D.120种
【答案】A
【详解】根据题意可知和都没有得到冠军,且不是最后一名,分两种情况:
①是最后一名,则可以为第二、三、四名,即有3种情况,剩下的三人安排在其他三个名次,
有种情况,此时有种名次排列情况;
②不是最后一名,,需要排在第二、三、四名,有种情况,剩下的三人安排在其他三个名次,有种情况,此时有种名次排列情况,则5人的名次排列方式共有种.
故选A.
【典例2】(2023上·上海·高二校考阶段练习)分别求下列情形的方法数:(用数字作答)
(1)从4名男生4名女生中选出2男2女组成一个队伍;
(2)8个人排成一排,其中甲乙二人必须站在一起;
(3)8个人排成一排,甲乙丙三人互相不能相邻.
【答案】(1)
(2)
(3)
【详解】(1)先从先从名男生中选出名,有种方法,
再从名女生中选出名,有种方法,
所以共有种方法.
(2)先把甲乙捆绑看成一个整体有种方法,再和其他人一起排列有种方法,
所以8个人排成一排,其中甲乙二人必须站在一起的方法为.
(3)先把其他人排列共有种方法,再把甲乙丙三人插空有,
所以个人排成一排,甲乙丙三人互相不能相邻的方法为.
【典例3】(2023上·高二课时练习)3名男生 4名女生排成一行.在下列要求下,分别求不同排列方法的种数:
(1)甲不在最左边,乙不在最右边;
(2)男生必须排在一起;
(3)男生和女生相间排列;
(4)在甲 乙两人中间必须有3人.
【答案】(1)
(2)
(3)
(4)
【详解】(1)依题意,先排最左边,除去甲外,有种,余下的6个位置全排有种,
但应剔除其中乙在最右边的排法数种,
则符合条件的排法共有种.
(2)将男生看成一个整体,进行全排列,有种排法,
再与其他元素进行全排列,有种排法,
故共有种.
(3)先排好男生,然后将女生插入男生所形成的四个空位,共有种.
(4)从除甲、乙以外的5人中选3人排在甲、乙中间的排法有种,
将甲、乙看作一个整体,和其余2人排成一排的排法有种,
最后再把选出的3人的排列插入到甲、乙之间即可,
共有种.
【变式1】(2023·四川凉山·统考一模)五名同学彝族新年期间去邛海湿地公园采风观景,在观鸟岛湿地门口五名同学排成一排照相留念,若甲与乙相邻,丙与丁不相邻,则不同的排法共有( )
A.12种 B.24种 C.48种 D.96种
【答案】B
【详解】甲和乙相邻,捆绑在一起有种,
再与丙和丁外的1人排列有种,
再排丙和丁有种,
故共有种排法.
故选:B.
【变式2】(2023上·辽宁朝阳·高二建平县实验中学校考期末)将0,1,2,3,4这五个数字组成无重复数字的五位数,则:
(1)可以组成多少个偶数?
(2)可以组成多少个比13123大的数?
【答案】(1)60;
(2)82.
【详解】(1)当个位数字为0时,可以组成个偶数;
当个位数字不为0时,可以组成个偶数;
所以可以组成个偶数.
(2)所组成的比13123大的五位数,可以分为以下2类:
第一类:形如,共有个,
第二类:形如,共有个,
所以可以组成个比13123大的数.
【变式3】(2023上·高二课时练习)(1)配制某种染色剂,需要加入种有机染料、种无机染料和种添加剂,其中有机染料的添加顺序不可以相邻.为研究所有不同的添加顺序对染色效果的影响,总共要试验多少次?
(2)某展览馆计划展出幅不同的画,其中水彩画幅、油画幅、国画幅.现排成一排陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端.问:有多少种不同的陈列方式?
【答案】(1);(2).
【详解】解:(1)先将种无机染料和种添加剂进行排序,
然后将种有机染料插入种无机染料和种添加剂所形成的个空位中的个,
由分步乘法计数原理可知,试验次数为;
(2)将幅油画捆绑,将幅国画捆绑,形成两个大元素,将水彩画放在“中间”,
将油画、国画放在两端,
故不同的陈列方式种数为种.
A夯实基础 B能力提升
A夯实基础
一、单选题
1.(2023下·北京通州·高二统考期中)计算:( )
A.30 B.60 C.90 D.120
【答案】D
【分析】根据排列数公式计算可得结果.
【详解】.
故选:D
2.(2023下·内蒙古乌兰察布·高二校考阶段练习)等于( )
A.107 B.323
C.320 D.348
【答案】D
【分析】根据排列数计算即可;
【详解】.
故选:D.
3.(2023下·广东江门·高二校考期中)用数字1,2,3,4,5组成的无重复数字的三位数的个数为( )
A.120 B.86 C.72 D.60
【答案】D
【分析】根据排列数计算出正确答案.
【详解】依题意,组成的无重复数字的三位数的个数为.
故选:D
4.(2023·四川乐山·统考一模)“数独九宫格”原创者是18世纪的瑞士数学家欧拉,它的游戏规则很简单,将1到9这九个自然数填到如图所示的小九宫格的9个空格里,每个空格填一个数,且9个空格的数字各不相同,若中间空格已填数字4,且只填第二行和第二列,并要求第二行从左至右及第二列从上至下所填的数字都是从大到小排列的,则不同的填法种数为( )
4
A.70 B.120 C.140 D.144
【答案】B
【分析】根据排列的知识求得正确答案.
【详解】比小的有,共个,从中选出个排在的左边和上方,方法数有种,
比大的有,共个,从中选出个排在的右边和下方,方法数有种,
所以不同的填法种数为种.
故选:B
5.(2023·全国·模拟预测)甲、乙,丙、丁,戊5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,裁判说:“很遗憾,你俩都没有得到冠军.但都不是最差的.”从回答分析,5人的名次排列的不同情况可能有( )
A.27种 B.72种 C.36种 D.54种
【答案】C
【分析】根据题意,先排甲乙,再排剩下三人,由排列数的计算,即可得到结果.
【详解】根据题意,甲、乙都没有得到冠军,也都不是最后一名,
先排甲乙,再排剩下三人,则5人的名次排列种数为种.
故选:C
6.(2023·河南开封·统考一模)现要从6名学生中选4名代表班级参加学校的接力赛,已知甲确定参加比赛且跑第1棒或第4棒,乙不能跑第1棒,则合适的选择方法种数为( )
A.84 B.108 C.132 D.144
【答案】B
【分析】特殊位置优先排,分类求解可得.
【详解】当甲跑第1棒时,则有种选择方法;
当甲跑第4棒时,乙参加比赛则有种选择方法,乙不参加比赛则有种选择方法.
故合适的选择方法种数为种.
故选:B
7.(2023上·甘肃白银·高三甘肃省靖远县第一中学校联考阶段练习)甲 乙 丙 丁等7人站成一排,其中甲 乙相邻,丁与甲 乙 丙都不相邻的站法共有( )
A.576种 B.448种 C.288种 D.224种
【答案】A
【分析】分两种情况讨论,第一种情况为丙和甲 乙中的1人相邻,优先排列甲 乙 丙位置,再将三人捆绑,将除丁外三人先排列,再将捆绑的整体和丁用插空法排列即可;第二种情况为若丙和甲 乙不相邻,先优先排列甲 乙位置后捆绑,再将除甲 乙 丙、丁外的三人先排列,最后用插空法将捆绑整体和丙、丁插空排列即可.
【详解】若丙和甲 乙中的1人相邻,则满足条件的站法共有种,
若丙和甲 乙不相邻,则满足条件的站法共有种,故总的站法共有576种.
故选:A
8.(2023下·广西防城港·高二防城港市高级中学校考期中)用数字0、1、2、3、4、5组成没有重复数字的四位数,若将组成的不重复的四位数按从小到大的顺序排成一个数列则第85个数字为( )
A.2301 B.2304 C.2305 D.2310
【答案】A
【分析】依次计算首位为1、前两位为20、前两位为21的有多少个数,然后可得答案.
【详解】首位为1的有个,前两位为20的有个,前两位为21的有个,
所以第85个数字是前两位为23的最小数,即为2301.
故选:A
二、多选题
9.(2023上·高二课时练习)(多选)用数字0,1,2,3,4,5组成没有重复数字的不同的所有四位数.下列结论正确的是( )
A. B.
C. D.-
【答案】CD
【分析】可用直接法先排第一位数字,再排后三位;也可用间接法先进行全排列,再排除首位是的情况.
【详解】(直接法)先排第一位,有种方法,再排后三位有种方法,所以共有种排法;
(间接法)先进行全排列共有种排法,首位是的排法为,所以共有-排法,
故选:
10.(2023下·江西·高一江西师大附中校考阶段练习)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B两人站在一起有48种方法
B.若A、B不相邻共有12种方法
C.若A在B左边有60种排法
D.若A不站在最左边,B不站最右边,有72种方法
【答案】AC
【分析】对于A:利用捆绑法,结合排列数运算求解;对于B:利用间接法,在总体中排除A、B两人站在一起的情况;对于C:根据对称性分析求解;对于D:利用间接法,结合组合数运算求解.
【详解】对于选项A:若A、B两人站在一起,则有种方法,故A正确;
对于选项B:A、B、C、D、E五个人并排站在一起,则有种方法,
所以A、B不相邻共有种方法,故B错误;
对于选项C:根据对称可知A在B左边有种排法,故C正确;
对于选项D:A站在最左边,则有种方法,
B站最右边,则有种方法,
A站在最左边,B站最右边,则有种方法,
所以A不站在最左边,B不站最右边,有种方法,故D错误.
故选:AC
三、填空题
11.(2023上·上海长宁·高三上海市延安中学校考期中)从甲 乙等5人中任选3人参加三个不同项目的比赛,要求每个项目都有人参加,则甲 乙中至少有1人入选的不同参赛方案共有 种.
【答案】54
【分析】根据排列数利用间接法,在总体中排除没有甲、乙的参赛方案.
【详解】若甲 乙等5人中任选3人参加三个不同项目的比赛,共有种不同参赛方案,
若没有甲 乙入选的不同参赛方案共有种,
所以甲 乙中至少有1人入选的不同参赛方案共有种.
故答案为:54.
12.(2023上·广东东莞·高三校考阶段练习)某中学为庆祝建校130周年,高二年级派出甲 乙 丙 丁 戊5名老师参加“130周年办学成果展”活动,活动结束后5名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有 种(用数字作答).
【答案】24
【分析】应用捆绑、插空法,结合分步计数及排列数求不同的排法数.
【详解】将丙、丁捆绑排列有种,再把他们作为整体与戊排成一排有种,
排完后其中有3个空,最后将甲、乙插入其中的两个空有种,
综上,共有种排法.
故答案为:
四、解答题
13.(2023·全国·高二专题练习)解不等式:;
【答案】
【分析】根据排列数公式得到不等式,解得即可.
【详解】因为,,,
所以不等式可化为,
解得,又,,
所以不等式的解集为.
14.(2023上·陕西汉中·高二西乡县第一中学校考阶段练习)电影《志愿军雄兵出击》讲述了在极其简陋的装备和极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神取得入朝作战第一阶段战役的胜利,著名的“松骨峰战斗”在该电影中就有场景.现有3名男生和4名女生相约一起去观看该影片,他们的座位在同一排且连在一起.(列出算式,并计算出结果)
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种?
【答案】(1)576
(2)144
(3)960
【分析】(1)由捆绑法即可得到结果;
(2)由插空法即可得到结果;
(3)结合捆绑法与插空法代入计算,即可得到结果.
【详解】(1)先将4名女生排在一起,有种排法,
将排好的女生视为一个整体,再与3名男生进行排列,共有种排法,
由分步乘法计数原理,共有种排法;
(2)先将3名男生排好,共有种排法,
在这3名男生中间以及两边的4个空位中插入4名女生,共有种排法,
再由分步乘法计数原理,共有种排法;
(3)先将甲乙丙以外的其余4人排好,共有种排法,
由于甲乙相邻,则有种排法,
最后将排好的甲乙这个整体与丙分别插入原先排好的4人的5个空隙中,
共有种排法,
由分步计数原理,共有种排法.
B能力提升
1.(2023·江苏南京·南京师大附中校考一模)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中a,b,c,d均为自然数,则满足条件的有序数组的个数是 .
【答案】28
【分析】分类讨论四个数的组成后,由计数原理求解即可.
【详解】显然a,b,c,d均为不超过5的自然数,下面进行讨论.
最大数为5的情况:
①,此时共有种情况;
最大数为4的情况:
②,此时共有种情况;
③,此时共有种情况.
当最大数为3时,,故没有满足题意的情况.
综上,满足条件的有序数组的个数是.
故答案为:28.
2.(2023下·重庆沙坪坝·高二重庆一中校考阶段练习)数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数.设,其中均为自然数,则满足条件的有序数组的个数是 .
【答案】29
【分析】分类讨论四个数的组成后,由计数原理求解
【详解】显然a,b,c,d均为不超过6的自然数,下面进行讨论.
最大数为6的情况:
①,此时共有种情况;
最大数为5的情况:
②,此时共有种情况;
当最大数为4时,
③,此时共有种情况;
当最大数为3时,
③,此时共有种情况;
综上,满足条件的有序数组的个数是.
故答案为:29.
3.(2023上·山东德州·高二校考阶段练习)名男生和名女生站成一排.
(1)甲不在中间也不在两端的站法有多少种?
(2)甲、乙两人必须站在两端的站法有多少种?
(3)男、女分别排在一起的站法有多少种?
(4)男、女相间的站法有多少种?
(5)甲、乙、丙三人从左到右顺序一定的站法有多少种?
【答案】(1)种
(2)种
(3)种
(4)种
(5)种
【分析】(1)按有特殊位置元素的排列方法求解;
(2)按有特殊位置元素的排列方法求解;
(3)按捆绑法排列即可;
(4)按插空法排列即可;
(5)按部分均匀的排列方法求解即可.
【详解】(1)先排甲有种,其余有种,
共有种排法.
(2)先排甲、乙,再排其余人,
共有种排法.
(3)把男生和女生分别看成一个元素,
男生和女生内部还有一个全排列,共种.
(4)先排名男生有种方法,
再将名女生插在男生形成的个空上有种方法,
故共有种排法.
(5)人共有种排法,
其中甲、乙、丙三人有种排法,
因而在种排法中每种对应一种符合条件的排法,
故共有种排法.
4.(2023·全国·高三专题练习)如图,用四种不同的颜色给三棱柱的六个顶点涂色,要求每个点涂一种颜色.
(1)若每个底面的顶点涂色所使用的颜色不相同,则不同的涂色方法共有多少种?
(2)若每条棱的两个端点涂不同的颜色,则不同的涂色方法共有多少种?
【答案】(1)576
(2)264
【详解】(1)由题得每个底面的顶点涂色所使用的颜色不相同,第一步,、、三点所涂颜色各不相同的方法有(种),第二步,、、三点所涂颜色各不相同的方法有(种),
所以由分步计数原理,不同的涂色方法共有(种).
(2)若用四种颜色,即,,,各涂一种颜色,与同色,与同色,所以有(种);
若用三种颜色,即第一类: 与同色、、各涂一种颜色,则只能涂剩余那种颜色,可以与或同色,所以有(种),
第二类:与同色、、各涂一种颜色,则只能涂剩余那种颜色,可以与或同色,所以有(种),
第三类:与同色、、各涂一种颜色,则可以涂剩余那种颜色或与同色,可以与同色或涂剩余那种颜色,所以有(种),
所以用三种颜色,有(种);
若用两种颜色,即与同色、与同色各涂一种颜色,可以涂剩余剩余两种颜色,也可以涂剩余剩余两种颜色,所以有(种).
所以由分类加法计数原理,共有(种).
5.(2023下·江苏镇江·高二校考期中)有3名男生与4名女生,在下列不同条件下,分别求排法种数.
(1)全体排成一排,女生必须站在一起;
(2)全体排成一排,男生互不相邻;
(3)全体排成一行,其中甲,乙,丙三人从左至右的顺序不变
【答案】(1)576
(2)1440
(3)840
【详解】(1)将女生看成一个整体,与名男生在一起进行全排列,有种方法,
再将名女生进行全排列,也有种方法,
故共有种排法.
(2)男生不相邻,而女生不作要求,所以应先排女生,有种方法,
再在女生之间及首尾空出的个空位中任选个空位排男生,有 种方法,
故共有种排法.
(3)从个位置中选四个安排除甲,乙,丙以外的个人,有种方法,
剩下的三个位置从左至右依次安排甲,乙,丙,仅有一种安排,
故共有种排法
21世纪教育网(www.21cnjy.com)
