人教版九年级数学上册重点压轴题专项讲练25.1统计与概率(重点题专项讲练)(学生版+解析)
文档属性
| 名称 | 人教版九年级数学上册重点压轴题专项讲练25.1统计与概率(重点题专项讲练)(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 21:15:25 | ||
图片预览




文档简介
专题25.1 统计与概率
【典例1】神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)________,________;并补全条形统计图:
(2)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;
(3)在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?
【思路点拨】
(1)根据A:航模制作的有10人,占10%可以求得m的值,从而可以求得n的值;根据题意和m的值可以求得B:航天资料收集;C:航天知识竞赛人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以估算出全校1800名学生中,大约有多少人选择参观科学馆;
(3)利用列表或树状图求概率即可
【解题过程】
解:(1)由题意可得,m=10÷10%=100,n%=100%-15%-10%-=35%,
故答案为:100,35;
由题意可得:B:航天资料收集有:100×35%=35(人)
C:航天知识竞赛有:100×15%=15(人)
补全条形统计图如图所示:
(2)(名),
答:估计该校大约有720名学生选择参观科学馆.
(3)解法一 列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
如上表,共有12种等可能的结果.其中恰好选中甲、乙两名同学的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
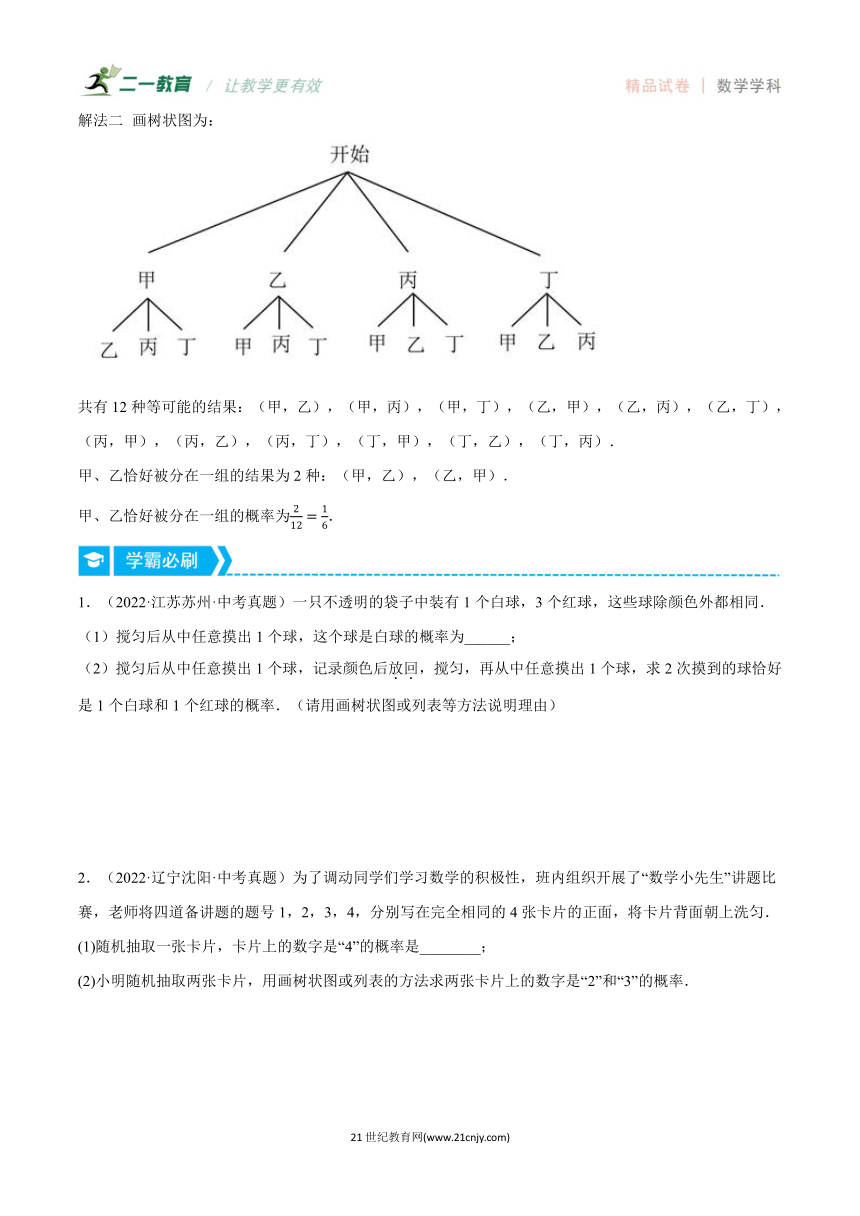
解法二 画树状图为:
共有12种等可能的结果:(甲,乙),(甲,丙),(甲,丁),(乙,甲),(乙,丙),(乙,丁),(丙,甲),(丙,乙),(丙,丁),(丁,甲),(丁,乙),(丁,丙).
甲、乙恰好被分在一组的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
1.(2022·江苏苏州·中考真题)一只不透明的袋子中装有1个白球,3个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为______;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
2.(2022·辽宁沈阳·中考真题)为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
3.(2022·山东青岛·中考真题)2022年3月23日下午,“天宫课堂”第二课开讲,航天员翟志刚、王亚平、叶光富相互配合进行授课,激发了同学们学习航天知识的热情.小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
4.(2022·辽宁鞍山·中考真题)2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一次国家安全知识竞赛,经过评比后,七年级的两名学生(用,表示)和八年级的两名学生(用,表示)获得优秀奖.
(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是_________.
(2)从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率.
5.(2022·内蒙古通辽·中考真题)如图,一个圆环被4条线段分成4个相等的区域,现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个,将这两个吉祥物放在任意两个区域内.
(1)求:吉祥物“冰墩墩”放在区域①的概率_______;
(2)求:吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率.(用树状图或列表法表示)
6.(2022·贵州遵义·中考真题)如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 6, 1,8,转盘乙上的数字分别是 4,5,7(规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是__________;转盘乙指针指向正数的概率是__________.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表法或树状图法求满足a+b<0的概率.
7.(2022·内蒙古内蒙古·中考真题)一个不透明的口袋中装有四个完全相同的小球,上面分别标有数字1,2,3,4.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是奇数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,在剩下的三个小球中再随机摸出一个小球,将小球上的数字记为y.请用列表或画树状图法,求由x,y确定的点在函数的图象上的概率.
8.(2022·辽宁锦州·中考真题)小华同学从一副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的甲盒中,再从这副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的乙盒中.
(1)小华同学从甲盒中随机抽取1张,抽到扑克牌花色为“红心”的概率为___________;
(2)小华同学从甲、乙两个盒中各随机抽取1张扑克牌.请用画树状图或列表的方法,求抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率.
9.(2022·湖南湘潭·中考真题)5月30日是全国科技工作者日,某校准备举办“走近科技英雄,讲好中国故事”的主题比赛活动.八年级(一)班由、、三名同学在班上进行初赛,推荐排名前两位的同学参加学校决赛.
(1)请写出在班上初赛时,这三名同学讲故事顺序的所有可能结果;
(2)若、两名同学参加学校决赛,学校制作了编号为、、的3张卡片(如图,除编号和内容外,其余完全相同),放在一个不透明的盒子里.先由随机摸取1张卡片记下编号,然后放回,再由随机摸取1张卡片记下编号,根据摸取的卡片内容讲述相关英雄的故事.求、两人恰好讲述同一名科技英雄故事的概率.(请用“画树状图”或“列表”等方法写出分析过程)
A“杂交水稻之父”袁隆平 B“天眼之父”南仁东 C“航天之父”钱学森
10.(2022·青海西宁·中考真题)“青绣”是我省非遗项目,其中土族盘绣、湟中堆绣、贵南藏绣、河湟刺绣等先后列入国家级、省级非物质文化遗产代表作名录.
(1)省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是________(填“全面调查”或“抽样调查”);
(2)为了增进我省青少年对“青绣”文化的了解,在一次社会实践活动中设置了转盘游戏.如图所示,一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上A,B,C,D(A代表土族盘绣、B代表湟中堆绣、C代表贵南藏绣、D代表河湟刺绣).游戏规则:每人转动转盘一次,当转盘停止时,指针落在哪个区域就获得相应的绣品(若指针落在分界线上,重转一次,直到指针指向某一区域内为止).请用画树状图或列表的方法求出甲、乙两名同学获得同一种绣品的概率,并列出所有等可能的结果.
11.(2022·四川雅安·中考真题)为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,结果如图所示.
(1)这50户家庭中5月用水量在20~30t的有多少户?
(2)把图中每组用水量的值用该组的中间值(如0~10的中间值为5)来代替,估计该小区平均每户用水量;
(3)从该50户用水量在20~40t的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在30~40t的概率.
12.(2022·广东深圳·中考真题)某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
13.(2022·山东淄博·中考真题)某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
请结合上述信息,解答下列问题:
(1)共有 名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是 度;
(2)补全调查结果条形统计图;
(3)小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.
14.(2022·辽宁丹东·中考真题)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取_____人,条形统计图中的m=______;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
15.(2022·湖北荆门·中考真题)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
16.(2022·山东日照·中考真题)今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
请根据统计图提供的信息,回答如下问题:
(1)x=________,y=________,并将直方图补充完整;
(2)已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是________,众数是________;
(3)若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;
(4)本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.
17.(2022·青海·中考真题)为迎接党的二十大胜利召开,某校对七、八年级的学生进行了党史学习宣传教育,其中七、八年级的学生各有500人.为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计、整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
八年级抽取学生的测试成绩条形统计图
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:______,______;
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
18.(2022·辽宁盘锦·中考真题)为更好的开展党史知识进校园活动,了解学生对党史知识的掌握程度,某校随机抽取了部分学生进行党史知识测试.并将测试结果分为A优秀,B良好,C合格,D不合格.将测试的结果绘制成如图所示的两幅不完整的统计图,请根据图中信息回答下列问题:
(1)本次调查了 名学生;
(2)补全条形统计图(并标注频数);
(3)扇形统计图中“B良好”所占扇形圆心角的度数为 度;
(4)该校共有800名学生,请你估计“良好”以上的学生有 名;
(5)在测试成绩为“优秀”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选2人参加市党史知识竞赛活动,请用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.
19.(2022·四川广安·中考真题)某校在开展线上教学期间,为了解七年级学生每天在家进行体育活动的时间(单位:h),随机调查了该年级的部分学生.根据调查结果,绘制出如下的扇形统计图1和条形统计图2,请根据相关信息,解答下列问题:
(1)本次随机调查的学生共有 人,图1中m的值为
(2)请补全条形统计图
(3)体育活动时间不足1小时的四人中有3名女生A1、A2、A3和1名男生B.为了解他们在家体育活动的实际情况,从这4人中随机抽取2人进行电话回访,请用列表法或画树状图法,求恰好抽到两名女生的概率
20.(2022·山东泰安·中考真题)2022年3月23日.“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:.C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了 名学生的成绩,频数直方图中,所抽取学生成绩的中位数落在 组;
(2)补全学生成绩频数直方图:
(3)若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?
(4)学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.21世纪教育网(www.21cnjy.com)
专题25.1 统计与概率
【典例1】神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)________,________;并补全条形统计图:
(2)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;
(3)在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?
【思路点拨】
(1)根据A:航模制作的有10人,占10%可以求得m的值,从而可以求得n的值;根据题意和m的值可以求得B:航天资料收集;C:航天知识竞赛人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以估算出全校1800名学生中,大约有多少人选择参观科学馆;
(3)利用列表或树状图求概率即可
【解题过程】
解:(1)由题意可得,m=10÷10%=100,n%=100%-15%-10%-=35%,
故答案为:100,35;
由题意可得:B:航天资料收集有:100×35%=35(人)
C:航天知识竞赛有:100×15%=15(人)
补全条形统计图如图所示:
(2)(名),
答:估计该校大约有720名学生选择参观科学馆.
(3)解法一 列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
如上表,共有12种等可能的结果.其中恰好选中甲、乙两名同学的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
解法二 画树状图为:
共有12种等可能的结果:(甲,乙),(甲,丙),(甲,丁),(乙,甲),(乙,丙),(乙,丁),(丙,甲),(丙,乙),(丙,丁),(丁,甲),(丁,乙),(丁,丙).
甲、乙恰好被分在一组的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
1.(2022·江苏苏州·中考真题)一只不透明的袋子中装有1个白球,3个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为______;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
【思路点拨】
(1)直接利用概率公式求解即可求得答案;
(2)画树状图表示所有等可能出现的情况,从中找出两个球颜色不同的结果数,进而求出概率.
【解题过程】
(1)解:∵一只不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同,
∴搅匀后从中任意摸出1个球,则摸出白球的概率为: .
故答案为:;
(2)解: 画树状图,如图所示:
共有16种不同的结果数,其中两个球颜色不同的有6种,
∴2次摸到的球恰好是1个白球和1个红球的概率为.
2.(2022·辽宁沈阳·中考真题)为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
【思路点拨】
(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,再由概率公式求解即可.
【解题过程】
(1)解:随机抽取一张卡片,卡片上的数字是4的概率为,
故答案为:;
(2)解:画树状图如下:
共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,
∴两张卡片上的数字是2和3的概率为.
3.(2022·山东青岛·中考真题)2022年3月23日下午,“天宫课堂”第二课开讲,航天员翟志刚、王亚平、叶光富相互配合进行授课,激发了同学们学习航天知识的热情.小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
【思路点拨】
根据题意列表求得双方的概率即可求解.
【解题过程】
解:所有可能的结果如下:
乙 甲 1 2 3 4 5
1
2
∴共有10种等可能的结果,其中两球编号之和为奇数的有5种结果,两球编号之和为偶数的有5种结果.
∴P(小冰获胜)
P(小雪获胜)
∵P(小冰获胜)=P(小雪获胜)
∴游戏对双方都公平.
4.(2022·辽宁鞍山·中考真题)2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一次国家安全知识竞赛,经过评比后,七年级的两名学生(用,表示)和八年级的两名学生(用,表示)获得优秀奖.
(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是_________.
(2)从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率.
【思路点拨】
(1)直接根据概率公式求解即可;
(2)画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
解:(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是,
故答案为:;
(2)树状图如下:
由表知,共有12种等可能结果,其中抽取的两名学生恰好一名来自七年级、一名来自八年级的有8种结果,
所以抽取的两名学生恰好一名来自七年级、一名来自八年级的概率为.
5.(2022·内蒙古通辽·中考真题)如图,一个圆环被4条线段分成4个相等的区域,现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个,将这两个吉祥物放在任意两个区域内.
(1)求:吉祥物“冰墩墩”放在区域①的概率_______;
(2)求:吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率.(用树状图或列表法表示)
【思路点拨】
(1)根据概率公式直接求解;
(2)根据列表法求概率即可求解.
【解题过程】
(1)吉祥物“冰墩墩”放在区域①的概率,
故答案为:
(2)
① ② ③ ④
① ①② ①③ ①④
② ②① ②③ ②④
③ ③① ③② ③④
④ ④① ④② ④③
共有12种等可能结果,吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的共有8种可能,
吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率为.
6.(2022·贵州遵义·中考真题)如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 6, 1,8,转盘乙上的数字分别是 4,5,7(规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是__________;转盘乙指针指向正数的概率是__________.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表法或树状图法求满足a+b<0的概率.
【思路点拨】
(1)直接根据概率公式求解即可;
(2)列表得出所有等可能解果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:转动转盘,转盘甲指针指向正数的概率是;
转盘乙指针指向正数的概率是.
故答案为:;.
(2)解:列表如下:
乙 甲 -1 -6 8
-4 -5 -10 4
5 4 -1 13
7 6 1 15
由表知,共有9种等可能结果,其中满足a+b<0的有3种结果,
∴满足a+b<0的概率为.
7.(2022·内蒙古内蒙古·中考真题)一个不透明的口袋中装有四个完全相同的小球,上面分别标有数字1,2,3,4.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是奇数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,在剩下的三个小球中再随机摸出一个小球,将小球上的数字记为y.请用列表或画树状图法,求由x,y确定的点在函数的图象上的概率.
【思路点拨】
(1)直接利用简单事件的概率公式计算可得;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与由x,y确定的点在函数的图象上的的情况,再利用概率公式求解即可求得答案.
【解题过程】
(1)解:P(奇数)
(2)解:列表得:
x y 1 2 3 4
1
2
3
4
共有12种等可能的结果,其中点在函数的图象上的有2种,
∴.P(点在函数的图象上)
8.(2022·辽宁锦州·中考真题)小华同学从一副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的甲盒中,再从这副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的乙盒中.
(1)小华同学从甲盒中随机抽取1张,抽到扑克牌花色为“红心”的概率为___________;
(2)小华同学从甲、乙两个盒中各随机抽取1张扑克牌.请用画树状图或列表的方法,求抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率.
【思路点拨】
(1)先求出从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1种,再利用概率公式求解;
(2)先列出表,进而得到从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑克牌花色恰好是1张“红心”和1张“方块”的结果有2种,利用概率公式求解.
【解题过程】
(1)解:根据题意可知
从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1种,
所以抽到扑克牌花色为“红心”的概率为.
故答案为:;
(2)解:列表如下:
红心甲 黑桃甲 方块甲 梅花甲
红心乙 红心甲,红心乙 黑桃甲,红心乙 方块甲,红心乙 梅花甲,红心乙
黑桃乙 红心甲,黑桃乙 黑桃甲,黑桃乙 方块甲,黑桃乙 梅花甲,黑桃乙
方块乙 红心甲,方块乙 黑桃甲,方块乙 方块甲,方块乙 梅花甲,方块乙
梅花乙 红心甲,梅花乙 黑桃甲,梅花乙 方块甲,梅花乙 梅花甲,梅花乙
从图中可知,从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑克牌花色恰好是1张“红心”和1张“方块”的结果有2种,
所以抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率是.
9.(2022·湖南湘潭·中考真题)5月30日是全国科技工作者日,某校准备举办“走近科技英雄,讲好中国故事”的主题比赛活动.八年级(一)班由、、三名同学在班上进行初赛,推荐排名前两位的同学参加学校决赛.
(1)请写出在班上初赛时,这三名同学讲故事顺序的所有可能结果;
(2)若、两名同学参加学校决赛,学校制作了编号为、、的3张卡片(如图,除编号和内容外,其余完全相同),放在一个不透明的盒子里.先由随机摸取1张卡片记下编号,然后放回,再由随机摸取1张卡片记下编号,根据摸取的卡片内容讲述相关英雄的故事.求、两人恰好讲述同一名科技英雄故事的概率.(请用“画树状图”或“列表”等方法写出分析过程)
A“杂交水稻之父”袁隆平 B“天眼之父”南仁东 C“航天之父”钱学森
【思路点拨】
(1)根据题意先画树状图列出所有等可能结果
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与A1A2抽取的都是同一名科技英雄的情况,再利用概率公式即可求得答案.
【解题过程】
(1)解:画树状图如下:
∴共有6种等可能的结果,分别是:①A1A2A3,②A1A3A2,③A2A1A3,④A2A3A1,⑤A3A1A2,⑥A3A2A1.
答:在班上初赛时,这三名同学讲故事顺序的所有可能结果为:①A1A2A3,②A1A3A2,③A2A1A3,④A2A3A1,⑤A3A1A2,⑥A3A2A1.
(2)解:画树状图如下:
∵由树状图知,共有9种等可能结果,其中、两人恰好讲述同一名科技英雄故事的结果有3种,
∴P(、两人恰好讲述同一名科技英雄故事)== ,
答:、两人恰好讲述同一名科技英雄故事的概率为.
10.(2022·青海西宁·中考真题)“青绣”是我省非遗项目,其中土族盘绣、湟中堆绣、贵南藏绣、河湟刺绣等先后列入国家级、省级非物质文化遗产代表作名录.
(1)省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是________(填“全面调查”或“抽样调查”);
(2)为了增进我省青少年对“青绣”文化的了解,在一次社会实践活动中设置了转盘游戏.如图所示,一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上A,B,C,D(A代表土族盘绣、B代表湟中堆绣、C代表贵南藏绣、D代表河湟刺绣).游戏规则:每人转动转盘一次,当转盘停止时,指针落在哪个区域就获得相应的绣品(若指针落在分界线上,重转一次,直到指针指向某一区域内为止).请用画树状图或列表的方法求出甲、乙两名同学获得同一种绣品的概率,并列出所有等可能的结果.
【思路点拨】
(1)选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,据此判定即可.
(2)利用列表法求解即可.
【解题过程】
(1)解:省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是抽样调查,
故答案为:抽样调查;
(2)解:列表如下:
甲 乙 A B C D
A AA BA CA DA
B AB BB CB DB
C AC BC CC DC
D AD BD CD DD
由表格可知,共有16种等可能结果,
其中甲、乙两名同学获得同一种绣品的结果共有4种,
即AA,BB,CC,DD
∴.
11.(2022·四川雅安·中考真题)为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,结果如图所示.
(1)这50户家庭中5月用水量在20~30t的有多少户?
(2)把图中每组用水量的值用该组的中间值(如0~10的中间值为5)来代替,估计该小区平均每户用水量;
(3)从该50户用水量在20~40t的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在30~40t的概率.
【思路点拨】
(1)由统计图可知,用50减去其他各组用水量的户数即可;
(2)根据题意找出各组的中间值,再用各组的中间值乘以各组的户数然后把它们的总和除以总户数即可.
(3)先列表展示所有20种等可能的结果数,再找出至少有1户用水量在30~40t的结果数,然后根据概率公式计算.
【解题过程】
(1)解: 50-20-25-2=3(户)
答:这50户家庭中5月用水量在20~30t的有3户.
(2)解:∵0~10的中间值为5;10~20的中间值为15;20~30的中间值为25;30~40的中间值为35;
∴(5×20+15×25+25×3+35×2)÷50=12.4(t).
答:估计该小区平均每户用水量为12.4t.
(3)解:用水量在20~30t的家庭用A表示,有3户,用水量在30~40t的家庭用B表示,有2户,任意抽取2户列表如下:
A1 A2 A3 B1 B2
A1 A1A2 A1A3 A1B1 A1B2
A2 A2A1 A2A3 A2B1 A2B2
A3 A3A1 A3A2 A3B1 A3B2
B1 B1A1 B1A2 B1A3 B1B2
B2 B2A1 B2A2 B2A3 B2B1
∵共有20种等可能结果,其中至少有1户用水量在30~40t的结果有14种,
∴P(至少有1户用水量在30~40t)==.
答:从该50户用水量在20~40t的家庭中,任抽取2户,至少有1户用水量在30~40t的概率是.
12.(2022·广东深圳·中考真题)某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
【思路点拨】
(1)由优秀人数及其所占百分比可得总人数,根据百分比之和为1可得合格人数所占百分比;
(2)总人数乘以不合格人数所占百分比求出其人数,从而补全图形;
(3)用乘以样本中“不合格人数”所占百分比即可得出答案;
(4)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:本次抽查的总人数为(人,
“合格”人数的百分比为,
故答案为:50人,;
(2)解:不合格的人数为:;
补全图形如下:
(3)解:扇形统计图中“不合格”人数的度数为,
故答案为:;
(4)解:列表如下:
甲 乙 丙
甲 (乙,甲) (丙,甲)
乙 (甲,乙) (丙,乙)
丙 (甲,丙) (乙,丙)
由表知,共有6种等可能结果,其中刚好抽中甲乙两人的有2种结果,
所以刚好抽中甲乙两人的概率为.
故答案为:.
13.(2022·山东淄博·中考真题)某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
请结合上述信息,解答下列问题:
(1)共有 名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是 度;
(2)补全调查结果条形统计图;
(3)小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.
【思路点拨】
(1)由选修“礼仪”的学生人数除以所占百分比得出参与了本次问卷调查的学生人数,即可解决问题;
(2)求出选修“厨艺”和“园艺”的学生人数,即可解决问题;
(3)画树状图,共有25种等可能的结果,其中小刚和小强两人恰好选到同一门课程的结果有5种,再由概率公式求解即可.
【解题过程】
(1)解:参与了本次问卷调查的学生人数为:(名),
则“陶艺”在扇形统计图中所对应的圆心角为:,
故答案为:120,99;
(2)解:条形统计图中,选修“厨艺”的学生人数为:(名),
则选修“园艺”的学生人数为:(名),
补全条形统计图如下:
(3)解:把“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程分别记为、、、、,
画树状图如下:
共有25种等可能的结果,其中小刚和小强两人恰好选到同一门课程的结果有5种,
小刚和小强两人恰好选到同一门课程的概率为.
14.(2022·辽宁丹东·中考真题)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取_____人,条形统计图中的m=______;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
【思路点拨】
(1)根据D组的人数和所占的百分比,求出调查的总人数,再用总人数乘以C所占的百分比,即可得出m的值;
(2)用360°乘以B组所占的百分比,求出B组的圆心角度数,再用总人数乘以B所占的百分比,即可得出B组的人数;
(3)用该校的总人数乘以达到3小时及3小时以上的学生所占的百分比即可;
(4)画树状图展示所有12种等可能的结果,再找出一名男生和一名女生的结果数,然后根据概率公式求解.
【解题过程】
(1)解:这次抽样调查共抽取的人数有:28÷28%=100(人),
m=100×42%=42,
故答案为:100,42;
(2)解:B组所在扇形圆心角的度数是:360°×20%=72°;
B组的人数有:100×20%=20(人),
补全统计图如下:
;
(3)解:根据题意得:
960×(42%+28%)=672(人),
答:估计该校一周累计劳动时间达到3小时及3小时以上的学生共有672人;
(4)解:画树状图为:
共有12种等可能的结果,其中抽取的两人恰好是一名男生和一名女生结果数为8,
所以抽取的两人恰好是一名男生和一名女生概率为.
15.(2022·湖北荆门·中考真题)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
【思路点拨】
(1)根据题意用20减去其他学生人数求得的值,根据表格数据求平均数即可求解;
(2)根据题意分别求得80≤x<90与97≤x≤100的人数所占的百分比,即可求得的值;
(3)先列表表示出所有可能的情况,然后再找出符合条件的情况数,最后利用概率公式进行求解即可
【解题过程】
解:(1)由题意可知,a=20﹣(2+1+3+2+1+3+2+1)=5,
∴a=5,
测评成绩的平均数=(88×2+89+90×5+91×3+95×2+96+97×3+98×2+99)=93,
补全的条形统计图如图所示:
(2)m%=×100%=15%;n%=×100%=30%;
所以m=15,n=30;
(3)根据题意列表得,设97分的用A1、A2、A3表示,98分的用B1、B2,表示,99分的用C表示,如图
A1 A2 A3 B1 B2 C
A1 A1A2 A1A3 A1B1 A1B2 A1C
A2 A2A1 A2A3 A2B1 A2B2 A2C
A3 A3A1 A3A2 A3B1 A3B2 A3C
B1 B1A1 B1A2 B1A3 B1B2 B1C
B2 B2A1 B2A2 B2A3 B2B1 B2C
C C A1 C A2 C A3 C B1 C B2
从6个人中选2个共有30个结果,一个97分,一个98分的有12种,
故概率为:=.
16.(2022·山东日照·中考真题)今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
请根据统计图提供的信息,回答如下问题:
(1)x=________,y=________,并将直方图补充完整;
(2)已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是________,众数是________;
(3)若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;
(4)本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.
【思路点拨】
(1)先求出被调查的总人数,继而可求得y、x的值;
(2)将数据重新排列,再根据中位数和众数的概念求解即可;
(3)用总人数乘以样本中优秀人数所占百分比即可;
(4)画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:被调查的总人数为4÷8%=50(人),
∴优秀对应的百分比,
则一般对应的人数为50-(4+23+8)=15(人),
∴其对应的百分比,
补全图形如下:
故答案为:30%,16%.
(2)解:将这组数据重新排列为91,93,94,94,96,98,99,100,
所以其中位数为,出现次数最多的是94,故众数为94,
故答案为:95,94;
(3)解:估计该校学生对团史掌握程度达到优秀的人数为1200×16%=192(人);
答:估计该校学生对团史掌握程度达到优秀的人数为192人 .
(4)解:画树状图为:
共有12种等可能情况,其中被抽取的2人恰好是女生的有6种结果,
所以恰好抽中2名女生参加知识竞赛的概率为.
17.(2022·青海·中考真题)为迎接党的二十大胜利召开,某校对七、八年级的学生进行了党史学习宣传教育,其中七、八年级的学生各有500人.为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计、整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
八年级抽取学生的测试成绩条形统计图
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:______,______;
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
【思路点拨】
(1)由众数和中位数的定义求解即可;
(2)七、八年级的平均数和中位数相同,七年级的优秀率大于八年级的优秀率,即可求解;
(3)由七、八年级的总人数分别乘以优秀率,再相加即可;
(4)画树状图,共有12种等可能的结果,被选中的2人恰好是七、八年级各1人的结果有6种,再由概率公式求解即可.
【解题过程】
(1)解:(1)由众数的定义得∶a=8,
八年级抽取学生的测试成绩的中位数为8(分),
故答案为∶8,8;
(2)解:答案一:七年级较好.理由:七年级被抽取的学生的成绩的众数是8分,八年级被抽取的学生的成绩的众数是7分,从这一统计量看,七年级学生党史知识掌握得较好.
答案二:七年级较好.理由:七年级被抽取的学生的成绩的优秀率是80%,八年级被抽取的学生的成绩的优秀率是60%,从这一统计量看,七年级学生党史知识掌握得较好.
(3)解:解:(人).
答:七、八年级学生对党史知识掌握能够达到优秀的总人数约为700人.
(4)解:列表如下:
第一人 第二人 八1 八2 八3 七
八1 (八1,八2) (八1,八3) (八1,七)
八2 (八2,八1) (八2,八3) (八2,七)
八3 (八3,八1) (八3,八2) (八3,七)
七 (七,八1) (七,八2) (七,八3)
或树状图如下:
由表格或树状图可知,共有12种等可能的情况,其中被选中的2人恰好是七、八年级各1人的情况有6种.
被选中的2人恰好是七、八年级各1人的概率.
18.(2022·辽宁盘锦·中考真题)为更好的开展党史知识进校园活动,了解学生对党史知识的掌握程度,某校随机抽取了部分学生进行党史知识测试.并将测试结果分为A优秀,B良好,C合格,D不合格.将测试的结果绘制成如图所示的两幅不完整的统计图,请根据图中信息回答下列问题:
(1)本次调查了 名学生;
(2)补全条形统计图(并标注频数);
(3)扇形统计图中“B良好”所占扇形圆心角的度数为 度;
(4)该校共有800名学生,请你估计“良好”以上的学生有 名;
(5)在测试成绩为“优秀”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选2人参加市党史知识竞赛活动,请用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.
【思路点拨】
(1)由优秀的人数除以所占百分比即可;
(2)求出C合格的人数,补全条形统计图即可;
(3)由360°乘以“B良好”所占的比例即可;
(4)由该校共有学生人数乘以“良好”以上的学生所占的比例即可;
(5)画树状图,共有12种等可能的结果,其中被选中的两人恰好是一男一女的结果有6种,再由概率公式求解即可.
【解题过程】
(1)解:本次调查中,一共调查学生15÷30%=50(名),
故答案为:50;
(2)解:C类别人数为50-(15+10+5)=20(人),
补全图形如下:
(3)解:“B良好”人数所在扇形的圆心角是360°×=72°,
故答案为:72;
(4)解:估计此次综合测试C类别的学生有800×=400(名).
(5)
解:
共有12种等可能的结果,其中被选中的两人恰好是一男一女的结果有6种,
∴被选中的两人恰好是一男一女的概率为=.
19.(2022·四川广安·中考真题)某校在开展线上教学期间,为了解七年级学生每天在家进行体育活动的时间(单位:h),随机调查了该年级的部分学生.根据调查结果,绘制出如下的扇形统计图1和条形统计图2,请根据相关信息,解答下列问题:
(1)本次随机调查的学生共有 人,图1中m的值为
(2)请补全条形统计图
(3)体育活动时间不足1小时的四人中有3名女生A1、A2、A3和1名男生B.为了解他们在家体育活动的实际情况,从这4人中随机抽取2人进行电话回访,请用列表法或画树状图法,求恰好抽到两名女生的概率
【思路点拨】
(1)用运动时间为0.9h的人数除以其所占比例即可求出总调查人数,总调查人数减去运动时间为0.9h、1.5h、1.8h、2.1h的人数之和即可的运动时间为1.2h的人数,在该人数除以总调查人数即可求出m的值;
(2)根据(1)中的数据补全图形即可;
(3)用列表法列举即可求解.
【解题过程】
解:(1)总调查人数4÷10%=40(人),
运动时间1.2h的人数为:40-(4+15+12+3)=6(人),
即其所占比例为:m%=6÷40=15%,
故m=15,
故答案为:40,15;
(2)补全图形如下:
(3)列表法列举如下:
总的可能情况有12种,刚好抽到两名女生的情况有6种,
即恰好抽到两名女的概率为:6÷12=,
故所求概率为.
20.(2022·山东泰安·中考真题)2022年3月23日.“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:.C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了 名学生的成绩,频数直方图中,所抽取学生成绩的中位数落在 组;
(2)补全学生成绩频数直方图:
(3)若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?
(4)学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
【思路点拨】
(1)用C组的人数除以C组所占的百分比可得总人数,再用总人数乘以B组所占的百分比,可求出m,从而得到第200位和201位数落在D组,即可求解;
(2)求出E租的人数,即可求解;
(3)用学校总人数乘以成绩优秀的学生所占的百分比,即可求解;
(4)根据题意,画树状图,可得共有20种等可能的结果,恰好抽中一名男生和一名女生的结果有12种,再根据概率公式计算,即可求解.
【解题过程】
(1)解:名,
所以本次调查一天随机抽取 400 名学生的成绩,
频数直方图中,
∴第200位和201位数落在D组,
即所抽取学生成绩的中位数落在D组;
故答案为:400,D
(2)解:E组的人数为名,
补全学生成绩频数直方图如下图:
(3)解:该校成绩优秀的学生有(人);
(4)解:根据题意,画树状图如图,
共有20种等可能的结果,恰好抽中一名男生和一名女生的结果有12种,
恰好抽中一名男生和一名女生的概率为.21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
【典例1】神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)________,________;并补全条形统计图:
(2)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;
(3)在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?
【思路点拨】
(1)根据A:航模制作的有10人,占10%可以求得m的值,从而可以求得n的值;根据题意和m的值可以求得B:航天资料收集;C:航天知识竞赛人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以估算出全校1800名学生中,大约有多少人选择参观科学馆;
(3)利用列表或树状图求概率即可
【解题过程】
解:(1)由题意可得,m=10÷10%=100,n%=100%-15%-10%-=35%,
故答案为:100,35;
由题意可得:B:航天资料收集有:100×35%=35(人)
C:航天知识竞赛有:100×15%=15(人)
补全条形统计图如图所示:
(2)(名),
答:估计该校大约有720名学生选择参观科学馆.
(3)解法一 列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
如上表,共有12种等可能的结果.其中恰好选中甲、乙两名同学的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
解法二 画树状图为:
共有12种等可能的结果:(甲,乙),(甲,丙),(甲,丁),(乙,甲),(乙,丙),(乙,丁),(丙,甲),(丙,乙),(丙,丁),(丁,甲),(丁,乙),(丁,丙).
甲、乙恰好被分在一组的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
1.(2022·江苏苏州·中考真题)一只不透明的袋子中装有1个白球,3个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为______;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
2.(2022·辽宁沈阳·中考真题)为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
3.(2022·山东青岛·中考真题)2022年3月23日下午,“天宫课堂”第二课开讲,航天员翟志刚、王亚平、叶光富相互配合进行授课,激发了同学们学习航天知识的热情.小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
4.(2022·辽宁鞍山·中考真题)2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一次国家安全知识竞赛,经过评比后,七年级的两名学生(用,表示)和八年级的两名学生(用,表示)获得优秀奖.
(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是_________.
(2)从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率.
5.(2022·内蒙古通辽·中考真题)如图,一个圆环被4条线段分成4个相等的区域,现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个,将这两个吉祥物放在任意两个区域内.
(1)求:吉祥物“冰墩墩”放在区域①的概率_______;
(2)求:吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率.(用树状图或列表法表示)
6.(2022·贵州遵义·中考真题)如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 6, 1,8,转盘乙上的数字分别是 4,5,7(规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是__________;转盘乙指针指向正数的概率是__________.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表法或树状图法求满足a+b<0的概率.
7.(2022·内蒙古内蒙古·中考真题)一个不透明的口袋中装有四个完全相同的小球,上面分别标有数字1,2,3,4.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是奇数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,在剩下的三个小球中再随机摸出一个小球,将小球上的数字记为y.请用列表或画树状图法,求由x,y确定的点在函数的图象上的概率.
8.(2022·辽宁锦州·中考真题)小华同学从一副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的甲盒中,再从这副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的乙盒中.
(1)小华同学从甲盒中随机抽取1张,抽到扑克牌花色为“红心”的概率为___________;
(2)小华同学从甲、乙两个盒中各随机抽取1张扑克牌.请用画树状图或列表的方法,求抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率.
9.(2022·湖南湘潭·中考真题)5月30日是全国科技工作者日,某校准备举办“走近科技英雄,讲好中国故事”的主题比赛活动.八年级(一)班由、、三名同学在班上进行初赛,推荐排名前两位的同学参加学校决赛.
(1)请写出在班上初赛时,这三名同学讲故事顺序的所有可能结果;
(2)若、两名同学参加学校决赛,学校制作了编号为、、的3张卡片(如图,除编号和内容外,其余完全相同),放在一个不透明的盒子里.先由随机摸取1张卡片记下编号,然后放回,再由随机摸取1张卡片记下编号,根据摸取的卡片内容讲述相关英雄的故事.求、两人恰好讲述同一名科技英雄故事的概率.(请用“画树状图”或“列表”等方法写出分析过程)
A“杂交水稻之父”袁隆平 B“天眼之父”南仁东 C“航天之父”钱学森
10.(2022·青海西宁·中考真题)“青绣”是我省非遗项目,其中土族盘绣、湟中堆绣、贵南藏绣、河湟刺绣等先后列入国家级、省级非物质文化遗产代表作名录.
(1)省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是________(填“全面调查”或“抽样调查”);
(2)为了增进我省青少年对“青绣”文化的了解,在一次社会实践活动中设置了转盘游戏.如图所示,一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上A,B,C,D(A代表土族盘绣、B代表湟中堆绣、C代表贵南藏绣、D代表河湟刺绣).游戏规则:每人转动转盘一次,当转盘停止时,指针落在哪个区域就获得相应的绣品(若指针落在分界线上,重转一次,直到指针指向某一区域内为止).请用画树状图或列表的方法求出甲、乙两名同学获得同一种绣品的概率,并列出所有等可能的结果.
11.(2022·四川雅安·中考真题)为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,结果如图所示.
(1)这50户家庭中5月用水量在20~30t的有多少户?
(2)把图中每组用水量的值用该组的中间值(如0~10的中间值为5)来代替,估计该小区平均每户用水量;
(3)从该50户用水量在20~40t的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在30~40t的概率.
12.(2022·广东深圳·中考真题)某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
13.(2022·山东淄博·中考真题)某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
请结合上述信息,解答下列问题:
(1)共有 名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是 度;
(2)补全调查结果条形统计图;
(3)小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.
14.(2022·辽宁丹东·中考真题)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取_____人,条形统计图中的m=______;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
15.(2022·湖北荆门·中考真题)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
16.(2022·山东日照·中考真题)今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
请根据统计图提供的信息,回答如下问题:
(1)x=________,y=________,并将直方图补充完整;
(2)已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是________,众数是________;
(3)若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;
(4)本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.
17.(2022·青海·中考真题)为迎接党的二十大胜利召开,某校对七、八年级的学生进行了党史学习宣传教育,其中七、八年级的学生各有500人.为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计、整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
八年级抽取学生的测试成绩条形统计图
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:______,______;
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
18.(2022·辽宁盘锦·中考真题)为更好的开展党史知识进校园活动,了解学生对党史知识的掌握程度,某校随机抽取了部分学生进行党史知识测试.并将测试结果分为A优秀,B良好,C合格,D不合格.将测试的结果绘制成如图所示的两幅不完整的统计图,请根据图中信息回答下列问题:
(1)本次调查了 名学生;
(2)补全条形统计图(并标注频数);
(3)扇形统计图中“B良好”所占扇形圆心角的度数为 度;
(4)该校共有800名学生,请你估计“良好”以上的学生有 名;
(5)在测试成绩为“优秀”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选2人参加市党史知识竞赛活动,请用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.
19.(2022·四川广安·中考真题)某校在开展线上教学期间,为了解七年级学生每天在家进行体育活动的时间(单位:h),随机调查了该年级的部分学生.根据调查结果,绘制出如下的扇形统计图1和条形统计图2,请根据相关信息,解答下列问题:
(1)本次随机调查的学生共有 人,图1中m的值为
(2)请补全条形统计图
(3)体育活动时间不足1小时的四人中有3名女生A1、A2、A3和1名男生B.为了解他们在家体育活动的实际情况,从这4人中随机抽取2人进行电话回访,请用列表法或画树状图法,求恰好抽到两名女生的概率
20.(2022·山东泰安·中考真题)2022年3月23日.“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:.C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了 名学生的成绩,频数直方图中,所抽取学生成绩的中位数落在 组;
(2)补全学生成绩频数直方图:
(3)若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?
(4)学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.21世纪教育网(www.21cnjy.com)
专题25.1 统计与概率
【典例1】神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)________,________;并补全条形统计图:
(2)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;
(3)在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?
【思路点拨】
(1)根据A:航模制作的有10人,占10%可以求得m的值,从而可以求得n的值;根据题意和m的值可以求得B:航天资料收集;C:航天知识竞赛人数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以估算出全校1800名学生中,大约有多少人选择参观科学馆;
(3)利用列表或树状图求概率即可
【解题过程】
解:(1)由题意可得,m=10÷10%=100,n%=100%-15%-10%-=35%,
故答案为:100,35;
由题意可得:B:航天资料收集有:100×35%=35(人)
C:航天知识竞赛有:100×15%=15(人)
补全条形统计图如图所示:
(2)(名),
答:估计该校大约有720名学生选择参观科学馆.
(3)解法一 列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
如上表,共有12种等可能的结果.其中恰好选中甲、乙两名同学的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
解法二 画树状图为:
共有12种等可能的结果:(甲,乙),(甲,丙),(甲,丁),(乙,甲),(乙,丙),(乙,丁),(丙,甲),(丙,乙),(丙,丁),(丁,甲),(丁,乙),(丁,丙).
甲、乙恰好被分在一组的结果为2种:(甲,乙),(乙,甲).
甲、乙恰好被分在一组的概率为.
1.(2022·江苏苏州·中考真题)一只不透明的袋子中装有1个白球,3个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为______;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
【思路点拨】
(1)直接利用概率公式求解即可求得答案;
(2)画树状图表示所有等可能出现的情况,从中找出两个球颜色不同的结果数,进而求出概率.
【解题过程】
(1)解:∵一只不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同,
∴搅匀后从中任意摸出1个球,则摸出白球的概率为: .
故答案为:;
(2)解: 画树状图,如图所示:
共有16种不同的结果数,其中两个球颜色不同的有6种,
∴2次摸到的球恰好是1个白球和1个红球的概率为.
2.(2022·辽宁沈阳·中考真题)为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
【思路点拨】
(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,再由概率公式求解即可.
【解题过程】
(1)解:随机抽取一张卡片,卡片上的数字是4的概率为,
故答案为:;
(2)解:画树状图如下:
共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,
∴两张卡片上的数字是2和3的概率为.
3.(2022·山东青岛·中考真题)2022年3月23日下午,“天宫课堂”第二课开讲,航天员翟志刚、王亚平、叶光富相互配合进行授课,激发了同学们学习航天知识的热情.小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
【思路点拨】
根据题意列表求得双方的概率即可求解.
【解题过程】
解:所有可能的结果如下:
乙 甲 1 2 3 4 5
1
2
∴共有10种等可能的结果,其中两球编号之和为奇数的有5种结果,两球编号之和为偶数的有5种结果.
∴P(小冰获胜)
P(小雪获胜)
∵P(小冰获胜)=P(小雪获胜)
∴游戏对双方都公平.
4.(2022·辽宁鞍山·中考真题)2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一次国家安全知识竞赛,经过评比后,七年级的两名学生(用,表示)和八年级的两名学生(用,表示)获得优秀奖.
(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是_________.
(2)从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率.
【思路点拨】
(1)直接根据概率公式求解即可;
(2)画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
解:(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是,
故答案为:;
(2)树状图如下:
由表知,共有12种等可能结果,其中抽取的两名学生恰好一名来自七年级、一名来自八年级的有8种结果,
所以抽取的两名学生恰好一名来自七年级、一名来自八年级的概率为.
5.(2022·内蒙古通辽·中考真题)如图,一个圆环被4条线段分成4个相等的区域,现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个,将这两个吉祥物放在任意两个区域内.
(1)求:吉祥物“冰墩墩”放在区域①的概率_______;
(2)求:吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率.(用树状图或列表法表示)
【思路点拨】
(1)根据概率公式直接求解;
(2)根据列表法求概率即可求解.
【解题过程】
(1)吉祥物“冰墩墩”放在区域①的概率,
故答案为:
(2)
① ② ③ ④
① ①② ①③ ①④
② ②① ②③ ②④
③ ③① ③② ③④
④ ④① ④② ④③
共有12种等可能结果,吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的共有8种可能,
吉祥物“冰墩墩”和“雪容融”放在相邻的两个区域的概率为.
6.(2022·贵州遵义·中考真题)如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 6, 1,8,转盘乙上的数字分别是 4,5,7(规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是__________;转盘乙指针指向正数的概率是__________.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表法或树状图法求满足a+b<0的概率.
【思路点拨】
(1)直接根据概率公式求解即可;
(2)列表得出所有等可能解果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:转动转盘,转盘甲指针指向正数的概率是;
转盘乙指针指向正数的概率是.
故答案为:;.
(2)解:列表如下:
乙 甲 -1 -6 8
-4 -5 -10 4
5 4 -1 13
7 6 1 15
由表知,共有9种等可能结果,其中满足a+b<0的有3种结果,
∴满足a+b<0的概率为.
7.(2022·内蒙古内蒙古·中考真题)一个不透明的口袋中装有四个完全相同的小球,上面分别标有数字1,2,3,4.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是奇数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,在剩下的三个小球中再随机摸出一个小球,将小球上的数字记为y.请用列表或画树状图法,求由x,y确定的点在函数的图象上的概率.
【思路点拨】
(1)直接利用简单事件的概率公式计算可得;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与由x,y确定的点在函数的图象上的的情况,再利用概率公式求解即可求得答案.
【解题过程】
(1)解:P(奇数)
(2)解:列表得:
x y 1 2 3 4
1
2
3
4
共有12种等可能的结果,其中点在函数的图象上的有2种,
∴.P(点在函数的图象上)
8.(2022·辽宁锦州·中考真题)小华同学从一副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的甲盒中,再从这副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的乙盒中.
(1)小华同学从甲盒中随机抽取1张,抽到扑克牌花色为“红心”的概率为___________;
(2)小华同学从甲、乙两个盒中各随机抽取1张扑克牌.请用画树状图或列表的方法,求抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率.
【思路点拨】
(1)先求出从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1种,再利用概率公式求解;
(2)先列出表,进而得到从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑克牌花色恰好是1张“红心”和1张“方块”的结果有2种,利用概率公式求解.
【解题过程】
(1)解:根据题意可知
从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1种,
所以抽到扑克牌花色为“红心”的概率为.
故答案为:;
(2)解:列表如下:
红心甲 黑桃甲 方块甲 梅花甲
红心乙 红心甲,红心乙 黑桃甲,红心乙 方块甲,红心乙 梅花甲,红心乙
黑桃乙 红心甲,黑桃乙 黑桃甲,黑桃乙 方块甲,黑桃乙 梅花甲,黑桃乙
方块乙 红心甲,方块乙 黑桃甲,方块乙 方块甲,方块乙 梅花甲,方块乙
梅花乙 红心甲,梅花乙 黑桃甲,梅花乙 方块甲,梅花乙 梅花甲,梅花乙
从图中可知,从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑克牌花色恰好是1张“红心”和1张“方块”的结果有2种,
所以抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率是.
9.(2022·湖南湘潭·中考真题)5月30日是全国科技工作者日,某校准备举办“走近科技英雄,讲好中国故事”的主题比赛活动.八年级(一)班由、、三名同学在班上进行初赛,推荐排名前两位的同学参加学校决赛.
(1)请写出在班上初赛时,这三名同学讲故事顺序的所有可能结果;
(2)若、两名同学参加学校决赛,学校制作了编号为、、的3张卡片(如图,除编号和内容外,其余完全相同),放在一个不透明的盒子里.先由随机摸取1张卡片记下编号,然后放回,再由随机摸取1张卡片记下编号,根据摸取的卡片内容讲述相关英雄的故事.求、两人恰好讲述同一名科技英雄故事的概率.(请用“画树状图”或“列表”等方法写出分析过程)
A“杂交水稻之父”袁隆平 B“天眼之父”南仁东 C“航天之父”钱学森
【思路点拨】
(1)根据题意先画树状图列出所有等可能结果
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与A1A2抽取的都是同一名科技英雄的情况,再利用概率公式即可求得答案.
【解题过程】
(1)解:画树状图如下:
∴共有6种等可能的结果,分别是:①A1A2A3,②A1A3A2,③A2A1A3,④A2A3A1,⑤A3A1A2,⑥A3A2A1.
答:在班上初赛时,这三名同学讲故事顺序的所有可能结果为:①A1A2A3,②A1A3A2,③A2A1A3,④A2A3A1,⑤A3A1A2,⑥A3A2A1.
(2)解:画树状图如下:
∵由树状图知,共有9种等可能结果,其中、两人恰好讲述同一名科技英雄故事的结果有3种,
∴P(、两人恰好讲述同一名科技英雄故事)== ,
答:、两人恰好讲述同一名科技英雄故事的概率为.
10.(2022·青海西宁·中考真题)“青绣”是我省非遗项目,其中土族盘绣、湟中堆绣、贵南藏绣、河湟刺绣等先后列入国家级、省级非物质文化遗产代表作名录.
(1)省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是________(填“全面调查”或“抽样调查”);
(2)为了增进我省青少年对“青绣”文化的了解,在一次社会实践活动中设置了转盘游戏.如图所示,一个可以自由转动的转盘,指针固定不动,转盘被分成了大小相同的4个扇形,并在每个扇形区域分别标上A,B,C,D(A代表土族盘绣、B代表湟中堆绣、C代表贵南藏绣、D代表河湟刺绣).游戏规则:每人转动转盘一次,当转盘停止时,指针落在哪个区域就获得相应的绣品(若指针落在分界线上,重转一次,直到指针指向某一区域内为止).请用画树状图或列表的方法求出甲、乙两名同学获得同一种绣品的概率,并列出所有等可能的结果.
【思路点拨】
(1)选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,据此判定即可.
(2)利用列表法求解即可.
【解题过程】
(1)解:省文旅厅为调查我省青少年对“青绣”文化的了解情况,应选择的调查方式是抽样调查,
故答案为:抽样调查;
(2)解:列表如下:
甲 乙 A B C D
A AA BA CA DA
B AB BB CB DB
C AC BC CC DC
D AD BD CD DD
由表格可知,共有16种等可能结果,
其中甲、乙两名同学获得同一种绣品的结果共有4种,
即AA,BB,CC,DD
∴.
11.(2022·四川雅安·中考真题)为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,结果如图所示.
(1)这50户家庭中5月用水量在20~30t的有多少户?
(2)把图中每组用水量的值用该组的中间值(如0~10的中间值为5)来代替,估计该小区平均每户用水量;
(3)从该50户用水量在20~40t的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在30~40t的概率.
【思路点拨】
(1)由统计图可知,用50减去其他各组用水量的户数即可;
(2)根据题意找出各组的中间值,再用各组的中间值乘以各组的户数然后把它们的总和除以总户数即可.
(3)先列表展示所有20种等可能的结果数,再找出至少有1户用水量在30~40t的结果数,然后根据概率公式计算.
【解题过程】
(1)解: 50-20-25-2=3(户)
答:这50户家庭中5月用水量在20~30t的有3户.
(2)解:∵0~10的中间值为5;10~20的中间值为15;20~30的中间值为25;30~40的中间值为35;
∴(5×20+15×25+25×3+35×2)÷50=12.4(t).
答:估计该小区平均每户用水量为12.4t.
(3)解:用水量在20~30t的家庭用A表示,有3户,用水量在30~40t的家庭用B表示,有2户,任意抽取2户列表如下:
A1 A2 A3 B1 B2
A1 A1A2 A1A3 A1B1 A1B2
A2 A2A1 A2A3 A2B1 A2B2
A3 A3A1 A3A2 A3B1 A3B2
B1 B1A1 B1A2 B1A3 B1B2
B2 B2A1 B2A2 B2A3 B2B1
∵共有20种等可能结果,其中至少有1户用水量在30~40t的结果有14种,
∴P(至少有1户用水量在30~40t)==.
答:从该50户用水量在20~40t的家庭中,任抽取2户,至少有1户用水量在30~40t的概率是.
12.(2022·广东深圳·中考真题)某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.
(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
【思路点拨】
(1)由优秀人数及其所占百分比可得总人数,根据百分比之和为1可得合格人数所占百分比;
(2)总人数乘以不合格人数所占百分比求出其人数,从而补全图形;
(3)用乘以样本中“不合格人数”所占百分比即可得出答案;
(4)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:本次抽查的总人数为(人,
“合格”人数的百分比为,
故答案为:50人,;
(2)解:不合格的人数为:;
补全图形如下:
(3)解:扇形统计图中“不合格”人数的度数为,
故答案为:;
(4)解:列表如下:
甲 乙 丙
甲 (乙,甲) (丙,甲)
乙 (甲,乙) (丙,乙)
丙 (甲,丙) (乙,丙)
由表知,共有6种等可能结果,其中刚好抽中甲乙两人的有2种结果,
所以刚好抽中甲乙两人的概率为.
故答案为:.
13.(2022·山东淄博·中考真题)某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
请结合上述信息,解答下列问题:
(1)共有 名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是 度;
(2)补全调查结果条形统计图;
(3)小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.
【思路点拨】
(1)由选修“礼仪”的学生人数除以所占百分比得出参与了本次问卷调查的学生人数,即可解决问题;
(2)求出选修“厨艺”和“园艺”的学生人数,即可解决问题;
(3)画树状图,共有25种等可能的结果,其中小刚和小强两人恰好选到同一门课程的结果有5种,再由概率公式求解即可.
【解题过程】
(1)解:参与了本次问卷调查的学生人数为:(名),
则“陶艺”在扇形统计图中所对应的圆心角为:,
故答案为:120,99;
(2)解:条形统计图中,选修“厨艺”的学生人数为:(名),
则选修“园艺”的学生人数为:(名),
补全条形统计图如下:
(3)解:把“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程分别记为、、、、,
画树状图如下:
共有25种等可能的结果,其中小刚和小强两人恰好选到同一门课程的结果有5种,
小刚和小强两人恰好选到同一门课程的概率为.
14.(2022·辽宁丹东·中考真题)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取_____人,条形统计图中的m=______;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
【思路点拨】
(1)根据D组的人数和所占的百分比,求出调查的总人数,再用总人数乘以C所占的百分比,即可得出m的值;
(2)用360°乘以B组所占的百分比,求出B组的圆心角度数,再用总人数乘以B所占的百分比,即可得出B组的人数;
(3)用该校的总人数乘以达到3小时及3小时以上的学生所占的百分比即可;
(4)画树状图展示所有12种等可能的结果,再找出一名男生和一名女生的结果数,然后根据概率公式求解.
【解题过程】
(1)解:这次抽样调查共抽取的人数有:28÷28%=100(人),
m=100×42%=42,
故答案为:100,42;
(2)解:B组所在扇形圆心角的度数是:360°×20%=72°;
B组的人数有:100×20%=20(人),
补全统计图如下:
;
(3)解:根据题意得:
960×(42%+28%)=672(人),
答:估计该校一周累计劳动时间达到3小时及3小时以上的学生共有672人;
(4)解:画树状图为:
共有12种等可能的结果,其中抽取的两人恰好是一名男生和一名女生结果数为8,
所以抽取的两人恰好是一名男生和一名女生概率为.
15.(2022·湖北荆门·中考真题)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
【思路点拨】
(1)根据题意用20减去其他学生人数求得的值,根据表格数据求平均数即可求解;
(2)根据题意分别求得80≤x<90与97≤x≤100的人数所占的百分比,即可求得的值;
(3)先列表表示出所有可能的情况,然后再找出符合条件的情况数,最后利用概率公式进行求解即可
【解题过程】
解:(1)由题意可知,a=20﹣(2+1+3+2+1+3+2+1)=5,
∴a=5,
测评成绩的平均数=(88×2+89+90×5+91×3+95×2+96+97×3+98×2+99)=93,
补全的条形统计图如图所示:
(2)m%=×100%=15%;n%=×100%=30%;
所以m=15,n=30;
(3)根据题意列表得,设97分的用A1、A2、A3表示,98分的用B1、B2,表示,99分的用C表示,如图
A1 A2 A3 B1 B2 C
A1 A1A2 A1A3 A1B1 A1B2 A1C
A2 A2A1 A2A3 A2B1 A2B2 A2C
A3 A3A1 A3A2 A3B1 A3B2 A3C
B1 B1A1 B1A2 B1A3 B1B2 B1C
B2 B2A1 B2A2 B2A3 B2B1 B2C
C C A1 C A2 C A3 C B1 C B2
从6个人中选2个共有30个结果,一个97分,一个98分的有12种,
故概率为:=.
16.(2022·山东日照·中考真题)今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
请根据统计图提供的信息,回答如下问题:
(1)x=________,y=________,并将直方图补充完整;
(2)已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是________,众数是________;
(3)若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;
(4)本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.
【思路点拨】
(1)先求出被调查的总人数,继而可求得y、x的值;
(2)将数据重新排列,再根据中位数和众数的概念求解即可;
(3)用总人数乘以样本中优秀人数所占百分比即可;
(4)画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解题过程】
(1)解:被调查的总人数为4÷8%=50(人),
∴优秀对应的百分比,
则一般对应的人数为50-(4+23+8)=15(人),
∴其对应的百分比,
补全图形如下:
故答案为:30%,16%.
(2)解:将这组数据重新排列为91,93,94,94,96,98,99,100,
所以其中位数为,出现次数最多的是94,故众数为94,
故答案为:95,94;
(3)解:估计该校学生对团史掌握程度达到优秀的人数为1200×16%=192(人);
答:估计该校学生对团史掌握程度达到优秀的人数为192人 .
(4)解:画树状图为:
共有12种等可能情况,其中被抽取的2人恰好是女生的有6种结果,
所以恰好抽中2名女生参加知识竞赛的概率为.
17.(2022·青海·中考真题)为迎接党的二十大胜利召开,某校对七、八年级的学生进行了党史学习宣传教育,其中七、八年级的学生各有500人.为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及8分以上为优秀),相关数据统计、整理如下:
七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
八年级抽取学生的测试成绩条形统计图
七、八年级抽取学生的测试成绩统计表
年级 七年级 八年级
平均数 8 8
众数 a 7
中位数 8 b
优秀率 80% 60%
(1)填空:______,______;
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加党史知识竞赛,请用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
【思路点拨】
(1)由众数和中位数的定义求解即可;
(2)七、八年级的平均数和中位数相同,七年级的优秀率大于八年级的优秀率,即可求解;
(3)由七、八年级的总人数分别乘以优秀率,再相加即可;
(4)画树状图,共有12种等可能的结果,被选中的2人恰好是七、八年级各1人的结果有6种,再由概率公式求解即可.
【解题过程】
(1)解:(1)由众数的定义得∶a=8,
八年级抽取学生的测试成绩的中位数为8(分),
故答案为∶8,8;
(2)解:答案一:七年级较好.理由:七年级被抽取的学生的成绩的众数是8分,八年级被抽取的学生的成绩的众数是7分,从这一统计量看,七年级学生党史知识掌握得较好.
答案二:七年级较好.理由:七年级被抽取的学生的成绩的优秀率是80%,八年级被抽取的学生的成绩的优秀率是60%,从这一统计量看,七年级学生党史知识掌握得较好.
(3)解:解:(人).
答:七、八年级学生对党史知识掌握能够达到优秀的总人数约为700人.
(4)解:列表如下:
第一人 第二人 八1 八2 八3 七
八1 (八1,八2) (八1,八3) (八1,七)
八2 (八2,八1) (八2,八3) (八2,七)
八3 (八3,八1) (八3,八2) (八3,七)
七 (七,八1) (七,八2) (七,八3)
或树状图如下:
由表格或树状图可知,共有12种等可能的情况,其中被选中的2人恰好是七、八年级各1人的情况有6种.
被选中的2人恰好是七、八年级各1人的概率.
18.(2022·辽宁盘锦·中考真题)为更好的开展党史知识进校园活动,了解学生对党史知识的掌握程度,某校随机抽取了部分学生进行党史知识测试.并将测试结果分为A优秀,B良好,C合格,D不合格.将测试的结果绘制成如图所示的两幅不完整的统计图,请根据图中信息回答下列问题:
(1)本次调查了 名学生;
(2)补全条形统计图(并标注频数);
(3)扇形统计图中“B良好”所占扇形圆心角的度数为 度;
(4)该校共有800名学生,请你估计“良好”以上的学生有 名;
(5)在测试成绩为“优秀”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选2人参加市党史知识竞赛活动,请用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.
【思路点拨】
(1)由优秀的人数除以所占百分比即可;
(2)求出C合格的人数,补全条形统计图即可;
(3)由360°乘以“B良好”所占的比例即可;
(4)由该校共有学生人数乘以“良好”以上的学生所占的比例即可;
(5)画树状图,共有12种等可能的结果,其中被选中的两人恰好是一男一女的结果有6种,再由概率公式求解即可.
【解题过程】
(1)解:本次调查中,一共调查学生15÷30%=50(名),
故答案为:50;
(2)解:C类别人数为50-(15+10+5)=20(人),
补全图形如下:
(3)解:“B良好”人数所在扇形的圆心角是360°×=72°,
故答案为:72;
(4)解:估计此次综合测试C类别的学生有800×=400(名).
(5)
解:
共有12种等可能的结果,其中被选中的两人恰好是一男一女的结果有6种,
∴被选中的两人恰好是一男一女的概率为=.
19.(2022·四川广安·中考真题)某校在开展线上教学期间,为了解七年级学生每天在家进行体育活动的时间(单位:h),随机调查了该年级的部分学生.根据调查结果,绘制出如下的扇形统计图1和条形统计图2,请根据相关信息,解答下列问题:
(1)本次随机调查的学生共有 人,图1中m的值为
(2)请补全条形统计图
(3)体育活动时间不足1小时的四人中有3名女生A1、A2、A3和1名男生B.为了解他们在家体育活动的实际情况,从这4人中随机抽取2人进行电话回访,请用列表法或画树状图法,求恰好抽到两名女生的概率
【思路点拨】
(1)用运动时间为0.9h的人数除以其所占比例即可求出总调查人数,总调查人数减去运动时间为0.9h、1.5h、1.8h、2.1h的人数之和即可的运动时间为1.2h的人数,在该人数除以总调查人数即可求出m的值;
(2)根据(1)中的数据补全图形即可;
(3)用列表法列举即可求解.
【解题过程】
解:(1)总调查人数4÷10%=40(人),
运动时间1.2h的人数为:40-(4+15+12+3)=6(人),
即其所占比例为:m%=6÷40=15%,
故m=15,
故答案为:40,15;
(2)补全图形如下:
(3)列表法列举如下:
总的可能情况有12种,刚好抽到两名女生的情况有6种,
即恰好抽到两名女的概率为:6÷12=,
故所求概率为.
20.(2022·山东泰安·中考真题)2022年3月23日.“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:,B组:.C组:,D组:,E组:,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)本次调查一共随机抽取了 名学生的成绩,频数直方图中,所抽取学生成绩的中位数落在 组;
(2)补全学生成绩频数直方图:
(3)若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?
(4)学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
【思路点拨】
(1)用C组的人数除以C组所占的百分比可得总人数,再用总人数乘以B组所占的百分比,可求出m,从而得到第200位和201位数落在D组,即可求解;
(2)求出E租的人数,即可求解;
(3)用学校总人数乘以成绩优秀的学生所占的百分比,即可求解;
(4)根据题意,画树状图,可得共有20种等可能的结果,恰好抽中一名男生和一名女生的结果有12种,再根据概率公式计算,即可求解.
【解题过程】
(1)解:名,
所以本次调查一天随机抽取 400 名学生的成绩,
频数直方图中,
∴第200位和201位数落在D组,
即所抽取学生成绩的中位数落在D组;
故答案为:400,D
(2)解:E组的人数为名,
补全学生成绩频数直方图如下图:
(3)解:该校成绩优秀的学生有(人);
(4)解:根据题意,画树状图如图,
共有20种等可能的结果,恰好抽中一名男生和一名女生的结果有12种,
恰好抽中一名男生和一名女生的概率为.21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
