人教A版数学(选择性必修一讲义)第08讲拓展二:直线与平面所成角的传统法与向量法(学生版+解析)
文档属性
| 名称 | 人教A版数学(选择性必修一讲义)第08讲拓展二:直线与平面所成角的传统法与向量法(学生版+解析) | 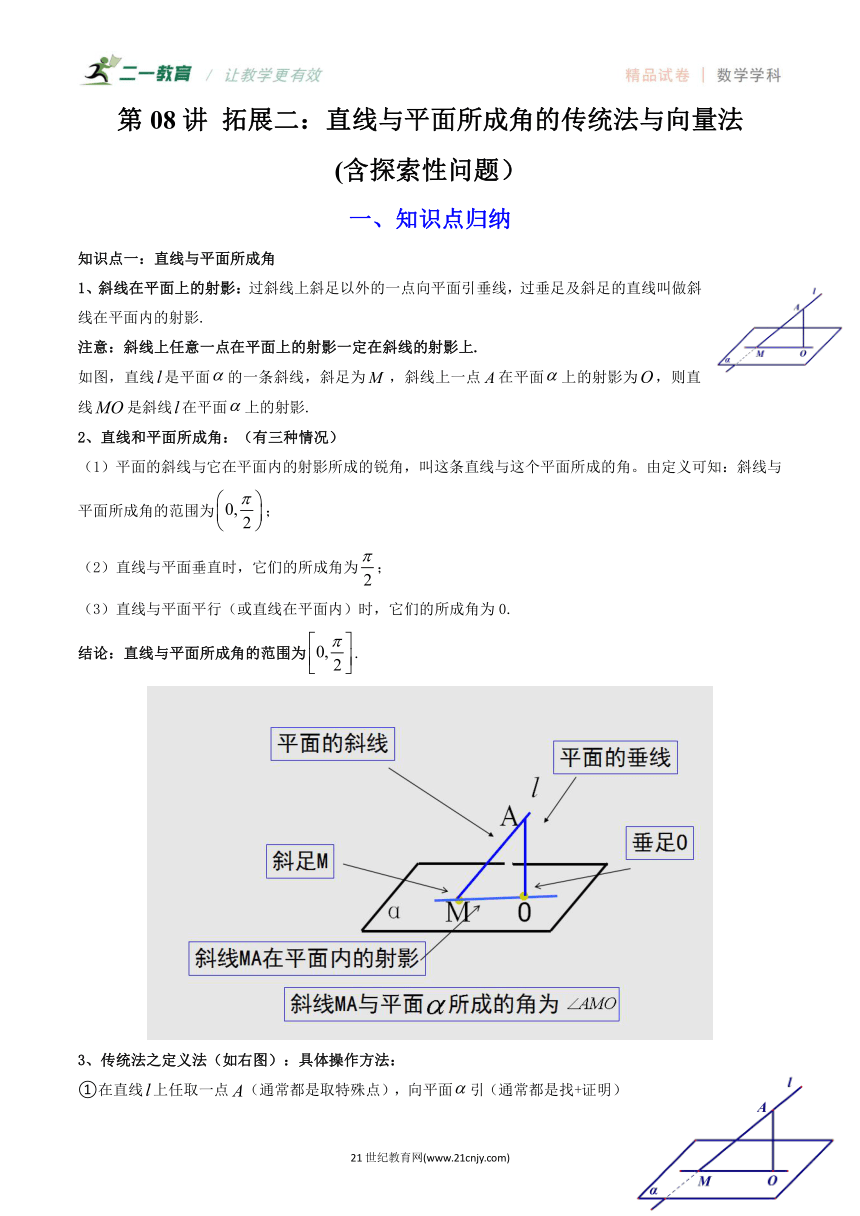 | |
| 格式 | docx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 09:53:10 | ||
图片预览




文档简介
第08讲 拓展二:直线与平面所成角的传统法与向量法
(含探索性问题)
一、知识点归纳
知识点一:直线与平面所成角
1、斜线在平面上的射影:过斜线上斜足以外的一点向平面引垂线,过垂足及斜足的直线叫做斜线在平面内的射影.
注意:斜线上任意一点在平面上的射影一定在斜线的射影上.
如图,直线是平面的一条斜线,斜足为,斜线上一点在平面上的射影为,则直线是斜线在平面上的射影.
2、直线和平面所成角:(有三种情况)
(1)平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个平面所成的角。由定义可知:斜线与平面所成角的范围为;
(2)直线与平面垂直时,它们的所成角为;
(3)直线与平面平行(或直线在平面内)时,它们的所成角为0.
结论:直线与平面所成角的范围为.
3、传统法之定义法(如右图):具体操作方法:
①在直线上任取一点(通常都是取特殊点),向平面引(通常都是找+证明)垂线;
②连接斜足与垂足;
③则斜线与射影所成的角,就是直线与平面所成角.
4、传统法之等体积法求垂线段法(如右图)
①利用等体积法求垂线段的长;
②
5、利用向量法求线面角
设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的角为,则有
①
②.(注意此公式中最后的形式是:)
二、题型精讲
题型01求直线与平面所成角(定值)(传统法)
【典例1】(2022秋·安徽·高三石室中学校联考阶段练习)在长方体中,,则与平面所成的正弦值为( )
A. B. C. D.
【典例2】(2022秋·上海闵行·高三上海市文来中学校考期中)在正方体中,为棱的中点,则与平面所成角的正切值为__________.
【典例3】(2022春·广东江门·高一江门市第一中学校考期中)如图,在四棱锥中,是边长为4的正方形的中心,平面,,分别为,的中点.
(1)求证:平面平面;
(2)若,求点到平面的距离;
(3)若,求直线与平面所成角的余弦值.
【典例4】(2022春·安徽滁州·高一统考期末)如图,平行六面体的棱长均相等,,点分别是棱的中点.
(1)求证:平面;
(2)求直线与底面所成角的正弦值.
【变式1】(2022春·广东广州·高一广州市第八十六中学校考期末)如图,在三棱锥中,底面,,且,是的中点,则与平面所成角的正弦值是________.
【变式2】(2022秋·贵州遵义·高二习水县第五中学校联考期末)如图,在四棱锥中,为线段的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
题型02求直线与平面所成角(定值)(向量法)
【典例1】(2023春·江苏连云港·高二统考期中)在正方体中,点,分别是,上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )
A. B. C. D.
【典例2】(2023秋·山东德州·高二统考期末)如图,已知直角梯形,,,,,四边形为正方形,且平面⊥平面.
(1)求证:⊥平面;
(2)点为线段的中点,求直线与平面所成角的正弦值.
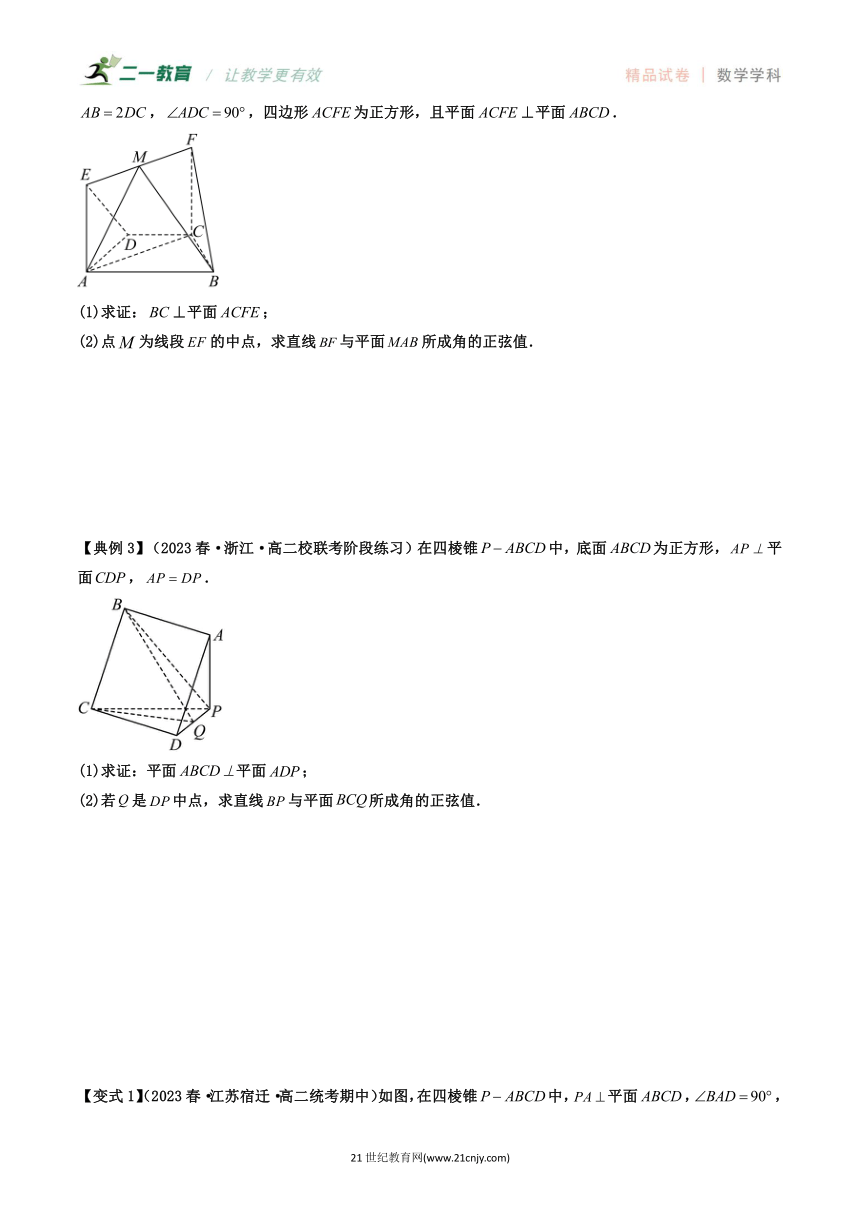
【典例3】(2023春·浙江·高二校联考阶段练习)在四棱锥中,底面为正方形,平面,.
(1)求证:平面平面;
(2)若是中点,求直线与平面所成角的正弦值.
【变式1】(2023春·江苏宿迁·高二统考期中)如图,在四棱锥中,平面,,,,已知是棱上靠近点的四等分点,则与平面所成角的正弦值为( ).
A. B. C. D.
【变式2】(2023春·广东广州·高二执信中学校考阶段练习)如图,四棱锥中,平面,,,,为棱上一点.
(1)若为的中点,证明:平面;
(2)若,且平面,求直线与平面所成角的正弦值.
【变式3】(2023春·福建宁德·高二校联考期中)在正四棱柱中,,,在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
题型03易错题型利用向量法求直线与平面所成角的余弦值
(忽视最后正弦转余弦)
【典例1】(2023·高二单元测试)已知四棱柱的底面是边长为2的正方形,侧棱与底面垂直,若点到平面的距离为,则直线与平面所成角的余弦值为( )
A. B. C. D.
【典例2】(2023春·甘肃金昌·高二永昌县第一高级中学校考期中)如图,已知平面,,,,,.若,,则与平面所成角的余弦值为__________.
【典例3】(2023春·江苏南京·高二南京市第五高级中学校考期中)如图,在底面为矩形的四棱锥中,平面平面.
(1)证明:;
(2)若,,设为中点,求直线与平面所成角的余弦值.
【变式1】(2023·全国·高三对口高考)正三棱柱的所有棱长都相等,则和平面所成角的余弦值为( )
A. B. C. D.
【变式2】(2023春·高二课时练习)若正三棱柱的所有棱长都相等,是的中点,则直线与平面所成角的余弦值为______.
【变式3】(2023·福建莆田·校考模拟预测)如图,在三棱锥中,,,,.
(1)证明:平面;
(2)求直线与平面所成角的余弦值.
题型04求直线与平面所成角(最值或范围)
【典例1】(2023春·高二课时练习)四棱锥,平面,底面是菱形,,平面平面.
(1)证明:⊥;
(2)设为上的点,求与平面所成角的正弦值的最大值.
【典例2】(2023·山东·校联考模拟预测)如图,圆锥的底面上有四点,且圆弧,点在线段上,若.
(1)证明:平面;
(2)若为等边三角形,点在劣弧上运动,记与平面所成的角为,求的最小值.
【典例3】(2023春·湖南长沙·高三长沙一中校考阶段练习)如图,在长方体中,点是长方形内一点,是二面角的平面角.
(1)证明:点在上;
(2)若,求直线与平面所成角的正弦的最大值.
【变式1】(2023春·江苏常州·高二江苏省溧阳中学校考阶段练习)如图,四棱锥的底面为正方形,底面,,点在棱上,且,点是棱上的动点(不含端点).
(1)若是棱的中点,求的余弦值;
(2)求与平面所成角的正弦值的最大值.
【变式2】(2023春·上海杨浦·高二上海市控江中学校考阶段练习)如图,在中,,,,可以通过以直线为轴旋转得到,且二面角是直二面角.动点在线段上.
(1)当为的中点时,求异面直线与所成角的余弦值;
(2)求与平面所成角的正弦最大值.
题型05已知直线与平面所成角求参数
【典例1】(2023春·江苏连云港·高二校考期中)如图所示空间直角坐标系中,是正三棱柱的底面内一动点,,直线和底面所成角为,则点坐标满足( )
A. B. C.D.
【典例2】(2023·全国·高三专题练习)在三棱锥中,,,互相垂直,,是线段上一动点,且直线与平面所成角的正切值的最大值是,则三棱锥外接球的体积是( )
A. B. C. D.
【典例3】(2023秋·重庆永川·高二重庆市永川北山中学校校考期末)如图,菱形中,,与相交于点,平面,,,.若直线与平面所成的角为45°,则=________.
【变式1】(2023·新疆喀什·统考模拟预测)如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为( )
A.1 B.2 C.3 D.4
【变式2】(2022·全国·高三专题练习)已知四面体中,,,两两垂直,,与平面所成角的正切值为,则点到平面的距离为( )
A. B. C. D.
【变式3】(2022秋·内蒙古赤峰·高二赤峰二中校考期末)已知几何体如图所示,其中四边形,,均为正方形,且边长为1,点在上,若直线与平面所成的角为45°,则___________.
题型06直线与平面所成角中的探索性问题
【典例1】(2023春·云南·高三云南师大附中校考阶段练习)如图,平行六面体的所有棱长都相等,,,为棱的中点,在棱上运动,.
(1)证明:当时,平面;
(2)是否存在点,使得直线与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
【典例2】(2023春·江苏连云港·高二校考期中)如图,在三棱柱中,平面,
平面互相垂直,,是线段上一点.
(1)设为的中点,求证:;
(2)若直线和平面所成角的正弦值为,求的值.
第08讲 拓展二:直线与平面所成角的传统法与向量法
(含探索性问题)
一、知识点归纳
知识点一:直线与平面所成角
1、斜线在平面上的射影:过斜线上斜足以外的一点向平面引垂线,过垂足及斜足的直线叫做斜线在平面内的射影.
注意:斜线上任意一点在平面上的射影一定在斜线的射影上.
如图,直线是平面的一条斜线,斜足为,斜线上一点在平面上的射影为,则直线是斜线在平面上的射影.
2、直线和平面所成角:(有三种情况)
(1)平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个平面所成的角。由定义可知:斜线与平面所成角的范围为;
(2)直线与平面垂直时,它们的所成角为;
(3)直线与平面平行(或直线在平面内)时,它们的所成角为0.
结论:直线与平面所成角的范围为.
3、传统法之定义法(如右图):具体操作方法:
①在直线上任取一点(通常都是取特殊点),向平面引(通常都是找+证明)垂线;
②连接斜足与垂足;
③则斜线与射影所成的角,就是直线与平面所成角.
4、传统法之等体积法求垂线段法(如右图)
①利用等体积法求垂线段的长;
②
5、利用向量法求线面角
设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的角为,则有
①
②.(注意此公式中最后的形式是:)
二、题型精讲
题型01求直线与平面所成角(定值)(传统法)
【典例1】(2022秋·安徽·高三石室中学校联考阶段练习)在长方体中,,则与平面所成的正弦值为( )
A. B. C. D.
【答案】C
【详解】设,连接OD,
因为,所以四边形为正方形,因此,
又平面,平面,故
又平面,因此平面,
所以BD与平面所成角为,
所以.
故选:C
【典例2】(2022秋·上海闵行·高三上海市文来中学校考期中)在正方体中,为棱的中点,则与平面所成角的正切值为__________.
【答案】/
【详解】
连接,
在正方体中, 平面,
是与平面所成的角,
,,
,
与平面所成的角的正切值为.
故答案为:.
【典例3】(2022春·广东江门·高一江门市第一中学校考期中)如图,在四棱锥中,是边长为4的正方形的中心,平面,,分别为,的中点.
(1)求证:平面平面;
(2)若,求点到平面的距离;
(3)若,求直线与平面所成角的余弦值.
【答案】(1)证明见解析
(2)
(3).
【详解】(1)因为四边形是正方形,所以,
因为平面,平面,所以,
因为平面,平面,且,
所以平面.又平面,所以平面平面.
(2)由(1)知,为点到平面的距离.
所以,
连接.因为平面,平面,所以,
因为,,所以,
又因为,所以.
在中,,,
所以,
设点到平面的距离为,
由,
得,所以.
所以点到平面的距离为.
(3)若,由(2)可知,点到平面的距离为,
又,
设直线与平面所成角为,
所以,
所以.
即直线与平面所成角的余弦值为.
【典例4】(2022春·安徽滁州·高一统考期末)如图,平行六面体的棱长均相等,,点分别是棱的中点.
(1)求证:平面;
(2)求直线与底面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)设的中点为,连接,
因为点分别是棱的中点,
所以,,
所以与平行且相等,四边形是平行四边形,则,
又因为平面,平面,
所以平面
(2)如图,设AC,BD交于点O,连接.
因为平行六面体中,设各棱长均为2,
因为,
所以为边长为2等边三角形,四边形ABCD为菱形,
所以O为BD的中点,.
所以.
因为,平面,所以平面.
等边三角形中,故.
解可得.
因为平面,平面,
所以平面平面,
故在平面ABCD上的射影Q落在AC上,连接,
所以
即到平面ABCD的距离为
所以到平面ABCD的距离为因为是棱的中点,
所以到平面ABCD的距离
因为,
所以直线与底面所成角的正弦值为
【变式1】(2022春·广东广州·高一广州市第八十六中学校考期末)如图,在三棱锥中,底面,,且,是的中点,则与平面所成角的正弦值是________.
【答案】/
【详解】如图,取中点,连接,
因为面,面,
所以,
又因为,
所以,
因为面,面,
所以,
又因为,所以,
因为面,,
所以面,
因为面,
所以,
因为面,
所以面,
所以是与平面所成角,
因为,,
所以,
由已证知,面,因为面,
所以,
所以,
因为面,面,
所以,
所以,
所以,
由已证知,面,
又因为面,所以
所以,
即与平面所成角的正弦值是.
故答案为:
【变式2】(2022秋·贵州遵义·高二习水县第五中学校联考期末)如图,在四棱锥中,为线段的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;
(2)
【详解】(1)连接,设,则有,
又在中,,则,,
等腰中,,,则
,
则中,,则,
又,,平面,
平面,
又平面,
.
(2)由(1)知:平面,
设到平面的距离为d,
又中,,
则
由
可得,
设直线与平面所成角为,
则.
题型02求直线与平面所成角(定值)(向量法)
【典例1】(2023春·江苏连云港·高二统考期中)在正方体中,点,分别是,上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )
A. B. C. D.
【答案】B
【详解】以为坐标原点,所在直线分别为轴,建立空间直角坐标系,
因为平面,平面,
所以,
因为正方形中,,且,平面,
所以⊥平面,
因为点M ,N分别是上的动点,
当点为交点时,⊥,过点作于点,
此时为的公垂线,即线段的长最小,
设正方体边长为,则,,
因为,所以,故,
解得:,,
过点作于点,同上可知,即,
解得:,,故,
,
又,则,
设平面的法向量为,
则,令,得,
设与平面所成角大小为,
则.
故选:B
【典例2】(2023秋·山东德州·高二统考期末)如图,已知直角梯形,,,,,四边形为正方形,且平面⊥平面.
(1)求证:⊥平面;
(2)点为线段的中点,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)已知直角梯形ABCD,,,
,所以为等腰直角三角形,
可得,,,
所以在中,由余弦定理得,
所以,得.
因为平面平面ABCD,平面平面,平面,
所以⊥平面.
(2)根据(1)中所证可得:两两垂直,
故以C为坐标原点,分别为轴建立如图所示空间直角坐标系:
则,,,.
,,,
设为平面MAB的一个法向量,
由,取,则,
故,
设直线与平面所成角为,
则.
即直线与平面所成角正弦值为.
【典例3】(2023春·浙江·高二校联考阶段练习)在四棱锥中,底面为正方形,平面,.
(1)求证:平面平面;
(2)若是中点,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)因为平面,平面,所以,
因为底面为正方形,所以,
又平面,所以平面,
又平面,所以平面平面.
(2)将题干图形调整一下位置,记的中点为,的中点为,连接,如图,
因为,是的中点,所以,
又由(1)知平面,平面,所以,
又平面,所以平面,
又是的中点,底面为正方形,所以,
故以为原点,为轴建立空间直角坐标系,如图,
因为平面,平面,所以,
不妨设,则在中,,
则,
因为是中点,则,
故,
设平面的一个法向量为,则,
取,则,故,
记直线与平面所成角为,则,
所以,
故直线与平面所成角的正弦值为.
【变式1】(2023春·江苏宿迁·高二统考期中)如图,在四棱锥中,平面,,,,已知是棱上靠近点的四等分点,则与平面所成角的正弦值为( ).
A. B. C. D.
【答案】C
【详解】平面,,
以为坐标原点,所在直线分别为轴、轴、轴,建立空间直角坐标系,则,.
.
易知平面的法向量.
设与平面所成角为,
则.
故选:C.
【变式2】(2023春·广东广州·高二执信中学校考阶段练习)如图,四棱锥中,平面,,,,为棱上一点.
(1)若为的中点,证明:平面;
(2)若,且平面,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)取中点,连接和,
因为,,且为的中点,
所以且,
所以四边形为平行四边形,则,
因为平面,平面,
所以平面,
因为M,N分别为的中点,
所以,
因为平面,平面,
所以平面,
又因为平面,,
所以平面平面,
因为平面,
所以平面
(2)取中点,作交于,连接,
因为,所以,
因为平面,平面,
所以,
因为,
所以,
以为坐标原点,为正交基底建立如下图所示的空间直角坐标系,
、、、、.
所以,.
设平面的法向量,
又因为平面,
所以,
取,,,则.
又因为,
所以.
所以直线和平面所成角正弦值为.
【变式3】(2023春·福建宁德·高二校联考期中)在正四棱柱中,,,在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;
(2).
【详解】(1)在正四棱柱中,两两垂直,
以的方向为轴的正方向建立空间直角坐标系,如图,
则,,,,,,
,,,
于是,,即且,
而平面DBE,
所以平面DBE.
(2)由(1)得,为平面DBE的一个法向量,
因此,
所以直线与平面DBE所成角的正弦值为.
题型03易错题型利用向量法求直线与平面所成角的余弦值
(忽视最后正弦转余弦)
【典例1】(2023·高二单元测试)已知四棱柱的底面是边长为2的正方形,侧棱与底面垂直,若点到平面的距离为,则直线与平面所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】如图,连接交于点,过点作于,
则平面,则,
设,
则,
则根据三角形面积得,
代入解得.
以为坐标原点,建立如图所示的空间直角坐标系.
则,,
设平面的法向量为,,,
则,即,令,得.
,
所以直线与平面所成的角的余弦值为,
故选:.
【典例2】(2023春·甘肃金昌·高二永昌县第一高级中学校考期中)如图,已知平面,,,,,.若,,则与平面所成角的余弦值为__________.
【答案】
【详解】
依题意,以为坐标原点,分别以,,为轴、轴、轴的正方向,如图建立空间直角坐标系,
由已知可得,,,,,,
则,,.
设是平面的法向量,
则,即,
令,则,,
所以是平面的一个法向量.
设与平面所成的角为,.
因为,,,
则,
所以.
因为,
所以,
所以与平面所成角的余弦值为.
故答案为:.
【典例3】(2023春·江苏南京·高二南京市第五高级中学校考期中)如图,在底面为矩形的四棱锥中,平面平面.
(1)证明:;
(2)若,,设为中点,求直线与平面所成角的余弦值.
【答案】(1)证明见解析;(2)
【详解】(1)依题意,面面,,
∵面,面面,
∴面.
又面,
∴.
(2)解法一:向量法
在中,取中点,∵,
∴,∴面,
以为坐标原点,分别以为轴,过点且平行于的直线为轴,所在的直线为轴,建立如图空间直角坐标系,
设,∵,∴,
∴,,,,,
∴,,.
设面法向量为,
则,解得.
设直线与平面所成角为,
则,
因为,∴.
所以直线与平面所成角的余弦值为.
(2)解法二:几何法
过作交于点,则为中点,
过作的平行线,过作的平行线,交点为,连结,
过作交于点,连结,
连结,取中点,连结,,
四边形为矩形,所以面,所以,
又,所以面,
所以为线与面所成的角.
令,则,,,
由同一个三角形面积相等可得,
为直角三角形,由勾股定理可得,
所以,
又因为为锐角,所以,
所以直线与平面所成角的余弦值为.
【变式1】(2023·全国·高三对口高考)正三棱柱的所有棱长都相等,则和平面所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】设三棱柱的棱长为1,以B为原点,以过B作的垂线为x轴,以为轴,
建立空间直角坐标系,如图,
则,∴,
平面的一个法向量可取为,
设与平面所成的角为θ,,
则,
所以.
故选:A.
【变式2】(2023春·高二课时练习)若正三棱柱的所有棱长都相等,是的中点,则直线与平面所成角的余弦值为______.
【答案】/0.6
【详解】
如图,取中点,连接,
则有,
所以以为轴正方向建系如图,设,
则,
设平面的法向量为,
则有,令则,
所以,
设直线与平面所成角为,
则,
因为,所以
故答案为: .
【变式3】(2023·福建莆田·校考模拟预测)如图,在三棱锥中,,,,.
(1)证明:平面;
(2)求直线与平面所成角的余弦值.
【答案】(1)证明见解析
(2)
【详解】(1)证明:,,,,
,,,
,,
,、平面, 平面,
平面,,
因为,、平面,平面.
(2)解:因为,平面,以点为坐标原点,、、的方向分别为、、轴的
正方向建立如下图所示的空间直角坐标系,
则、、、,
,,
设平面的一个法向量分别为,
则,取,可得,
,,
设直线与平面所成角的,则,,
直线与平面所成角的余弦值.
题型04求直线与平面所成角(最值或范围)
【典例1】(2023春·高二课时练习)四棱锥,平面,底面是菱形,,平面平面.
(1)证明:⊥;
(2)设为上的点,求与平面所成角的正弦值的最大值.
【答案】(1)证明过程见解析
(2)
【详解】(1)如图,过点A作AE⊥PB于点E,
因为平面平面PBC,交线为PB,且AE平面PAB,
所以AE⊥平面PBC,
因为平面PBC,
所以AE⊥BC,
因为平面ABCD,平面ABCD,
所以PA⊥BC,
因为,平面PAB,
所以BC⊥平面PAB,
因为AB平面PAB,
所以BC⊥AB;
(2)因为底面ABCD是菱形,且BC⊥AB,
所以四边形ABCD为正方形,
以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
设AB=1,则,
,
设,,
则,
设平面ABM的法向量为,
则,
解得:,不妨令,则,
故,
设PC与平面ABM所成角大小为,
则,
,
当时,取得最大值,最大值为,
所以PC与平面ABM所成角的正弦值的最大值为.
【典例2】(2023·山东·校联考模拟预测)如图,圆锥的底面上有四点,且圆弧,点在线段上,若.
(1)证明:平面;
(2)若为等边三角形,点在劣弧上运动,记与平面所成的角为,求的最小值.
【答案】(1)证明见解析
(2).
【详解】(1)∵,∴为等边三角形,
所以为底面圆的直径,设,
在中,,,
所以则,
,
设到底面的距离分别为,
即,
即,所以即.
设的交点为,所以,即,
连接,则,面面,
所以面.
(2)设底面圆的圆心为,过作,
以为坐标原点,的方向为轴建立空间直角坐标系,
因为,所以由可得:,
设,则,
设平面的一个法向量为
∴,所以可取
∴
当且仅当,即与重合时取等号.
所以的最小值为.
【典例3】(2023春·湖南长沙·高三长沙一中校考阶段练习)如图,在长方体中,点是长方形内一点,是二面角的平面角.
(1)证明:点在上;
(2)若,求直线与平面所成角的正弦的最大值.
【答案】(1)证明见解析
(2)
【详解】(1)由是二面角的平面角,则,
又,面,则面,
又面,即,由长方体性质知,故,
由长方体性质:面,又面,则,
又,面,故面,
而面面,且面、面,根据过AC作与PD1垂直的平面有且仅有一个,
所以面与面为同一平面,又面,面面,
所以点在上;
(2)构建如下图示的空间直角坐标系,令,,
由题设,长方体上下底面都为正方形,由(1)知,则为中点,
所以且,,,
则,,,
若是面的一个法向量,则,令,则,
所以,
仅当时等号成立,故直线与平面所成角的正弦的最大值为.
【变式1】(2023春·江苏常州·高二江苏省溧阳中学校考阶段练习)如图,四棱锥的底面为正方形,底面,,点在棱上,且,点是棱上的动点(不含端点).
(1)若是棱的中点,求的余弦值;
(2)求与平面所成角的正弦值的最大值.
【答案】(1)
(2)
【详解】(1)由平面,,平面,所以,,
又,所以、、两两垂直,
以为坐标原点,分别以,,所在直线为,,轴,建立空间直角坐标系,
则,,,,,,
当为棱的中点时,,则,,
,
所以的余弦值为.
(2),设,,
则,则,又,
设平面的一个法向量为,
则,即,取,
,设与平面所成角为,
,
令,当时,,
即时,有最大值,
所以与平面所成角的正弦值的最大值为.
【变式2】(2023春·上海杨浦·高二上海市控江中学校考阶段练习)如图,在中,,,,可以通过以直线为轴旋转得到,且二面角是直二面角.动点在线段上.
(1)当为的中点时,求异面直线与所成角的余弦值;
(2)求与平面所成角的正弦最大值.
【答案】(1)(2)
【详解】(1)由题意可得:,平面平面,
平面平面,平面,
所以平面,
如图,以为坐标原点建立空间直角坐标系,则,
若为的中点,则,
可得,
设异面直线与所成角,
则.
故异面直线与所成角的余弦值为.
(2)若动点在线段上,设,
则,可得,解得,
即,则,
由题意可知:平面的法向量为,
设与平面所成角为,
则,
对于开口向上,对称轴为,
可得当时,取到最小值,
所以的最大值为,
题型05已知直线与平面所成角求参数
【典例1】(2023春·江苏连云港·高二校考期中)如图所示空间直角坐标系中,是正三棱柱的底面内一动点,,直线和底面所成角为,则点坐标满足( )
A. B. C.D.
【答案】A
【详解】解:由正三棱柱,且,根据坐标系可得:
,又是正三棱柱的底面内一动点,则,所以,
又平面,所以是平面的一个法向量,
因为直线和底面所成角为,
所以,
整理得,又,所以.
故选:A.
【典例2】(2023·全国·高三专题练习)在三棱锥中,,,互相垂直,,是线段上一动点,且直线与平面所成角的正切值的最大值是,则三棱锥外接球的体积是( )
A. B. C. D.
【答案】D
【详解】M是线段BC上一动点,连接PM.因为PA,PB,PC互相垂直,所以是直线AM与平面PBC所成的角.当PM最短,即时,直线AM与平面PBC所成角的正切值最大,此时,.
在中,,则,解得.
将三棱锥扩充为长方体,则长方体的体对角线长为.
故三棱锥外接球的半径,三棱锥外接球的体积为.所以D正确;
故选:D.
【典例3】(2023秋·重庆永川·高二重庆市永川北山中学校校考期末)如图,菱形中,,与相交于点,平面,,,.若直线与平面所成的角为45°,则=________.
【答案】2
【详解】设AE=a,在菱形ABCD中,∠ABC=60°,则△ABC为正三角形,又AB=2,易得OA=1,OB=,
如图,以O为坐标原点,以OA,OB所在直线分别为x轴、y轴,以过点O且平行于CF的直线为z轴建立空间直角坐标系.
则,
所以,设平面BED的法向量为,则,令z=1则,,
因为直线OF与平面BED所成角的大小为45°,
所以,
易知a>0,解得:a=2,所以AE=2.
故答案为:2.
【变式1】(2023·新疆喀什·统考模拟预测)如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为( )
A.1 B.2 C.3 D.4
【答案】D
【详解】以为原点,以,,为坐标轴建立空间坐标系如图所示,
设,则,,,
故,,,
设平面的一个法向量为,
则,可取,
故,
又直线与平面所成角的正弦值为,
,解得.
故选:D
【变式2】(2022·全国·高三专题练习)已知四面体中,,,两两垂直,,与平面所成角的正切值为,则点到平面的距离为( )
A. B. C. D.
【答案】D
【详解】以为原点,,,分别为,,轴建立空间直角坐标系,如图所示:
设,,,,,.
,,.
设平面的法向量,
则,令,得,,
故.
因为直线与平面所成角的正切值为,
所以直线与平面所成角的正弦值为.
即,解得.
所以平面的法向量,
故到平面的距离为.
故选:D
【变式3】(2022秋·内蒙古赤峰·高二赤峰二中校考期末)已知几何体如图所示,其中四边形,,均为正方形,且边长为1,点在上,若直线与平面所成的角为45°,则___________.
【答案】/
【详解】把该几何体补成一个正方体,如图,,连接,
由平面,平面,得,同理,.
又正方形中,,,平面,
所以平面,而平面,所以平面平面,
所以平面内的直线在平面上的射影是,即是直线MB与平面BEF所成的角,,
,
.
,.
故答案为:.
题型06直线与平面所成角中的探索性问题
【典例1】(2023春·云南·高三云南师大附中校考阶段练习)如图,平行六面体的所有棱长都相等,,,为棱的中点,在棱上运动,.
(1)证明:当时,平面;
(2)是否存在点,使得直线与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在,.
【详解】(1)证明:当时,为棱中点,
取中点为,连接,如图所示,
则,,
又因为,,
所以,
所以为平行四边形,
所以,
又因为平面,平面,
所以平面.
(2)存在当时,直线与平面所成角的正弦值为,理由如下:
不妨设棱长,则,
在中,,
所以,
同理可得,,
所以,
所以,
所以,
又因为在等边中,,
所以,
所以,
又因为,
所以以为原点,分别以、、为x轴、y轴、z轴建立空间直角坐标系如图所示,
则,,,,,,
则,,
所以,,
所以,,,
设平面的一个法向量为,
则,解得,
设直线与平面所成角为,
则,
解得(舍)或.
所以存在,直线与平面所成角的正弦值为.
【典例2】(2023春·江苏连云港·高二校考期中)如图,在三棱柱中,平面,,是的中点.
(1)求平面与平面夹角的余弦值;
(2)在直线上是否存在一点,使得与平面所成角的正弦值为,若存在,求出CP的长;若不存在,请说明理由.
【答案】(1)
(2)存在,或.
【详解】(1)因为平面ABC,平面ABC,则,,
以点C为坐标原点,建立空间直角坐标系,如图所示,
则,
所以平面ABC的一个法向量为,
设平面的法向量为,而,
所以,即,令,则,故,
所以,又平面与平面ABC夹角为锐角,
所以平面与平面ABC夹角的余弦值为;
(2)假设存在点P,
设,,
设BP与平面所成的角为,由(1)知,平面的法向量为,
则,
所以,解得或,
在线段CD上存在一点P,使BP与面所成角的正弦值为,此时或.
【变式1】(2023·福建漳州·统考模拟预测)如图,是圆的直径,点是圆上异于,的点,平面,,,,分别为,的中点,平面与平面的交线为,在圆上.
(1)在图中作出交线(说明画法,不必证明),并求三棱锥的体积;
(2)若点满足,且与平面所成角的正弦值为,求的值.
【答案】(1)答案见解析,
(2)或
【详解】(1)过点作交圆于点,( ,分别为,的中点,所以,又,所以,故为平面与平面的交线)
因为是圆的直径,所以,,
所以,所以四边形为矩形,
因为,,所以,
因为平面,为的中点,
所以点到平面的距离为,
所以
(2)以为坐标原点,分别以,,的方向作为轴,轴,轴的正方向建立空间直角坐标系,如图,
则,,,,,
所以,,,
,
设平面的法向量为,则
即,不妨取,得
因为与平面所成角的正弦值为,
所以
所以,所以或
【变式2】(2023·上海浦东新·华师大二附中校考三模)如图,直角三角形和等边三角形所在平面互相垂直,,是线段上一点.
令,则,.于是.
因为直线和平面所成角的正弦值为,
所以,
整理得,
解得或.
因为,
所以,即.
21世纪教育网(www.21cnjy.com)
(含探索性问题)
一、知识点归纳
知识点一:直线与平面所成角
1、斜线在平面上的射影:过斜线上斜足以外的一点向平面引垂线,过垂足及斜足的直线叫做斜线在平面内的射影.
注意:斜线上任意一点在平面上的射影一定在斜线的射影上.
如图,直线是平面的一条斜线,斜足为,斜线上一点在平面上的射影为,则直线是斜线在平面上的射影.
2、直线和平面所成角:(有三种情况)
(1)平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个平面所成的角。由定义可知:斜线与平面所成角的范围为;
(2)直线与平面垂直时,它们的所成角为;
(3)直线与平面平行(或直线在平面内)时,它们的所成角为0.
结论:直线与平面所成角的范围为.
3、传统法之定义法(如右图):具体操作方法:
①在直线上任取一点(通常都是取特殊点),向平面引(通常都是找+证明)垂线;
②连接斜足与垂足;
③则斜线与射影所成的角,就是直线与平面所成角.
4、传统法之等体积法求垂线段法(如右图)
①利用等体积法求垂线段的长;
②
5、利用向量法求线面角
设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的角为,则有
①
②.(注意此公式中最后的形式是:)
二、题型精讲
题型01求直线与平面所成角(定值)(传统法)
【典例1】(2022秋·安徽·高三石室中学校联考阶段练习)在长方体中,,则与平面所成的正弦值为( )
A. B. C. D.
【典例2】(2022秋·上海闵行·高三上海市文来中学校考期中)在正方体中,为棱的中点,则与平面所成角的正切值为__________.
【典例3】(2022春·广东江门·高一江门市第一中学校考期中)如图,在四棱锥中,是边长为4的正方形的中心,平面,,分别为,的中点.
(1)求证:平面平面;
(2)若,求点到平面的距离;
(3)若,求直线与平面所成角的余弦值.
【典例4】(2022春·安徽滁州·高一统考期末)如图,平行六面体的棱长均相等,,点分别是棱的中点.
(1)求证:平面;
(2)求直线与底面所成角的正弦值.
【变式1】(2022春·广东广州·高一广州市第八十六中学校考期末)如图,在三棱锥中,底面,,且,是的中点,则与平面所成角的正弦值是________.
【变式2】(2022秋·贵州遵义·高二习水县第五中学校联考期末)如图,在四棱锥中,为线段的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
题型02求直线与平面所成角(定值)(向量法)
【典例1】(2023春·江苏连云港·高二统考期中)在正方体中,点,分别是,上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )
A. B. C. D.
【典例2】(2023秋·山东德州·高二统考期末)如图,已知直角梯形,,,,,四边形为正方形,且平面⊥平面.
(1)求证:⊥平面;
(2)点为线段的中点,求直线与平面所成角的正弦值.
【典例3】(2023春·浙江·高二校联考阶段练习)在四棱锥中,底面为正方形,平面,.
(1)求证:平面平面;
(2)若是中点,求直线与平面所成角的正弦值.
【变式1】(2023春·江苏宿迁·高二统考期中)如图,在四棱锥中,平面,,,,已知是棱上靠近点的四等分点,则与平面所成角的正弦值为( ).
A. B. C. D.
【变式2】(2023春·广东广州·高二执信中学校考阶段练习)如图,四棱锥中,平面,,,,为棱上一点.
(1)若为的中点,证明:平面;
(2)若,且平面,求直线与平面所成角的正弦值.
【变式3】(2023春·福建宁德·高二校联考期中)在正四棱柱中,,,在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
题型03易错题型利用向量法求直线与平面所成角的余弦值
(忽视最后正弦转余弦)
【典例1】(2023·高二单元测试)已知四棱柱的底面是边长为2的正方形,侧棱与底面垂直,若点到平面的距离为,则直线与平面所成角的余弦值为( )
A. B. C. D.
【典例2】(2023春·甘肃金昌·高二永昌县第一高级中学校考期中)如图,已知平面,,,,,.若,,则与平面所成角的余弦值为__________.
【典例3】(2023春·江苏南京·高二南京市第五高级中学校考期中)如图,在底面为矩形的四棱锥中,平面平面.
(1)证明:;
(2)若,,设为中点,求直线与平面所成角的余弦值.
【变式1】(2023·全国·高三对口高考)正三棱柱的所有棱长都相等,则和平面所成角的余弦值为( )
A. B. C. D.
【变式2】(2023春·高二课时练习)若正三棱柱的所有棱长都相等,是的中点,则直线与平面所成角的余弦值为______.
【变式3】(2023·福建莆田·校考模拟预测)如图,在三棱锥中,,,,.
(1)证明:平面;
(2)求直线与平面所成角的余弦值.
题型04求直线与平面所成角(最值或范围)
【典例1】(2023春·高二课时练习)四棱锥,平面,底面是菱形,,平面平面.
(1)证明:⊥;
(2)设为上的点,求与平面所成角的正弦值的最大值.
【典例2】(2023·山东·校联考模拟预测)如图,圆锥的底面上有四点,且圆弧,点在线段上,若.
(1)证明:平面;
(2)若为等边三角形,点在劣弧上运动,记与平面所成的角为,求的最小值.
【典例3】(2023春·湖南长沙·高三长沙一中校考阶段练习)如图,在长方体中,点是长方形内一点,是二面角的平面角.
(1)证明:点在上;
(2)若,求直线与平面所成角的正弦的最大值.
【变式1】(2023春·江苏常州·高二江苏省溧阳中学校考阶段练习)如图,四棱锥的底面为正方形,底面,,点在棱上,且,点是棱上的动点(不含端点).
(1)若是棱的中点,求的余弦值;
(2)求与平面所成角的正弦值的最大值.
【变式2】(2023春·上海杨浦·高二上海市控江中学校考阶段练习)如图,在中,,,,可以通过以直线为轴旋转得到,且二面角是直二面角.动点在线段上.
(1)当为的中点时,求异面直线与所成角的余弦值;
(2)求与平面所成角的正弦最大值.
题型05已知直线与平面所成角求参数
【典例1】(2023春·江苏连云港·高二校考期中)如图所示空间直角坐标系中,是正三棱柱的底面内一动点,,直线和底面所成角为,则点坐标满足( )
A. B. C.D.
【典例2】(2023·全国·高三专题练习)在三棱锥中,,,互相垂直,,是线段上一动点,且直线与平面所成角的正切值的最大值是,则三棱锥外接球的体积是( )
A. B. C. D.
【典例3】(2023秋·重庆永川·高二重庆市永川北山中学校校考期末)如图,菱形中,,与相交于点,平面,,,.若直线与平面所成的角为45°,则=________.
【变式1】(2023·新疆喀什·统考模拟预测)如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为( )
A.1 B.2 C.3 D.4
【变式2】(2022·全国·高三专题练习)已知四面体中,,,两两垂直,,与平面所成角的正切值为,则点到平面的距离为( )
A. B. C. D.
【变式3】(2022秋·内蒙古赤峰·高二赤峰二中校考期末)已知几何体如图所示,其中四边形,,均为正方形,且边长为1,点在上,若直线与平面所成的角为45°,则___________.
题型06直线与平面所成角中的探索性问题
【典例1】(2023春·云南·高三云南师大附中校考阶段练习)如图,平行六面体的所有棱长都相等,,,为棱的中点,在棱上运动,.
(1)证明:当时,平面;
(2)是否存在点,使得直线与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
【典例2】(2023春·江苏连云港·高二校考期中)如图,在三棱柱中,平面,
平面互相垂直,,是线段上一点.
(1)设为的中点,求证:;
(2)若直线和平面所成角的正弦值为,求的值.
第08讲 拓展二:直线与平面所成角的传统法与向量法
(含探索性问题)
一、知识点归纳
知识点一:直线与平面所成角
1、斜线在平面上的射影:过斜线上斜足以外的一点向平面引垂线,过垂足及斜足的直线叫做斜线在平面内的射影.
注意:斜线上任意一点在平面上的射影一定在斜线的射影上.
如图,直线是平面的一条斜线,斜足为,斜线上一点在平面上的射影为,则直线是斜线在平面上的射影.
2、直线和平面所成角:(有三种情况)
(1)平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个平面所成的角。由定义可知:斜线与平面所成角的范围为;
(2)直线与平面垂直时,它们的所成角为;
(3)直线与平面平行(或直线在平面内)时,它们的所成角为0.
结论:直线与平面所成角的范围为.
3、传统法之定义法(如右图):具体操作方法:
①在直线上任取一点(通常都是取特殊点),向平面引(通常都是找+证明)垂线;
②连接斜足与垂足;
③则斜线与射影所成的角,就是直线与平面所成角.
4、传统法之等体积法求垂线段法(如右图)
①利用等体积法求垂线段的长;
②
5、利用向量法求线面角
设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的角为,则有
①
②.(注意此公式中最后的形式是:)
二、题型精讲
题型01求直线与平面所成角(定值)(传统法)
【典例1】(2022秋·安徽·高三石室中学校联考阶段练习)在长方体中,,则与平面所成的正弦值为( )
A. B. C. D.
【答案】C
【详解】设,连接OD,
因为,所以四边形为正方形,因此,
又平面,平面,故
又平面,因此平面,
所以BD与平面所成角为,
所以.
故选:C
【典例2】(2022秋·上海闵行·高三上海市文来中学校考期中)在正方体中,为棱的中点,则与平面所成角的正切值为__________.
【答案】/
【详解】
连接,
在正方体中, 平面,
是与平面所成的角,
,,
,
与平面所成的角的正切值为.
故答案为:.
【典例3】(2022春·广东江门·高一江门市第一中学校考期中)如图,在四棱锥中,是边长为4的正方形的中心,平面,,分别为,的中点.
(1)求证:平面平面;
(2)若,求点到平面的距离;
(3)若,求直线与平面所成角的余弦值.
【答案】(1)证明见解析
(2)
(3).
【详解】(1)因为四边形是正方形,所以,
因为平面,平面,所以,
因为平面,平面,且,
所以平面.又平面,所以平面平面.
(2)由(1)知,为点到平面的距离.
所以,
连接.因为平面,平面,所以,
因为,,所以,
又因为,所以.
在中,,,
所以,
设点到平面的距离为,
由,
得,所以.
所以点到平面的距离为.
(3)若,由(2)可知,点到平面的距离为,
又,
设直线与平面所成角为,
所以,
所以.
即直线与平面所成角的余弦值为.
【典例4】(2022春·安徽滁州·高一统考期末)如图,平行六面体的棱长均相等,,点分别是棱的中点.
(1)求证:平面;
(2)求直线与底面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)设的中点为,连接,
因为点分别是棱的中点,
所以,,
所以与平行且相等,四边形是平行四边形,则,
又因为平面,平面,
所以平面
(2)如图,设AC,BD交于点O,连接.
因为平行六面体中,设各棱长均为2,
因为,
所以为边长为2等边三角形,四边形ABCD为菱形,
所以O为BD的中点,.
所以.
因为,平面,所以平面.
等边三角形中,故.
解可得.
因为平面,平面,
所以平面平面,
故在平面ABCD上的射影Q落在AC上,连接,
所以
即到平面ABCD的距离为
所以到平面ABCD的距离为因为是棱的中点,
所以到平面ABCD的距离
因为,
所以直线与底面所成角的正弦值为
【变式1】(2022春·广东广州·高一广州市第八十六中学校考期末)如图,在三棱锥中,底面,,且,是的中点,则与平面所成角的正弦值是________.
【答案】/
【详解】如图,取中点,连接,
因为面,面,
所以,
又因为,
所以,
因为面,面,
所以,
又因为,所以,
因为面,,
所以面,
因为面,
所以,
因为面,
所以面,
所以是与平面所成角,
因为,,
所以,
由已证知,面,因为面,
所以,
所以,
因为面,面,
所以,
所以,
所以,
由已证知,面,
又因为面,所以
所以,
即与平面所成角的正弦值是.
故答案为:
【变式2】(2022秋·贵州遵义·高二习水县第五中学校联考期末)如图,在四棱锥中,为线段的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;
(2)
【详解】(1)连接,设,则有,
又在中,,则,,
等腰中,,,则
,
则中,,则,
又,,平面,
平面,
又平面,
.
(2)由(1)知:平面,
设到平面的距离为d,
又中,,
则
由
可得,
设直线与平面所成角为,
则.
题型02求直线与平面所成角(定值)(向量法)
【典例1】(2023春·江苏连云港·高二统考期中)在正方体中,点,分别是,上的动点,当线段的长最小时,直线与平面所成角的正弦值为( )
A. B. C. D.
【答案】B
【详解】以为坐标原点,所在直线分别为轴,建立空间直角坐标系,
因为平面,平面,
所以,
因为正方形中,,且,平面,
所以⊥平面,
因为点M ,N分别是上的动点,
当点为交点时,⊥,过点作于点,
此时为的公垂线,即线段的长最小,
设正方体边长为,则,,
因为,所以,故,
解得:,,
过点作于点,同上可知,即,
解得:,,故,
,
又,则,
设平面的法向量为,
则,令,得,
设与平面所成角大小为,
则.
故选:B
【典例2】(2023秋·山东德州·高二统考期末)如图,已知直角梯形,,,,,四边形为正方形,且平面⊥平面.
(1)求证:⊥平面;
(2)点为线段的中点,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)已知直角梯形ABCD,,,
,所以为等腰直角三角形,
可得,,,
所以在中,由余弦定理得,
所以,得.
因为平面平面ABCD,平面平面,平面,
所以⊥平面.
(2)根据(1)中所证可得:两两垂直,
故以C为坐标原点,分别为轴建立如图所示空间直角坐标系:
则,,,.
,,,
设为平面MAB的一个法向量,
由,取,则,
故,
设直线与平面所成角为,
则.
即直线与平面所成角正弦值为.
【典例3】(2023春·浙江·高二校联考阶段练习)在四棱锥中,底面为正方形,平面,.
(1)求证:平面平面;
(2)若是中点,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)因为平面,平面,所以,
因为底面为正方形,所以,
又平面,所以平面,
又平面,所以平面平面.
(2)将题干图形调整一下位置,记的中点为,的中点为,连接,如图,
因为,是的中点,所以,
又由(1)知平面,平面,所以,
又平面,所以平面,
又是的中点,底面为正方形,所以,
故以为原点,为轴建立空间直角坐标系,如图,
因为平面,平面,所以,
不妨设,则在中,,
则,
因为是中点,则,
故,
设平面的一个法向量为,则,
取,则,故,
记直线与平面所成角为,则,
所以,
故直线与平面所成角的正弦值为.
【变式1】(2023春·江苏宿迁·高二统考期中)如图,在四棱锥中,平面,,,,已知是棱上靠近点的四等分点,则与平面所成角的正弦值为( ).
A. B. C. D.
【答案】C
【详解】平面,,
以为坐标原点,所在直线分别为轴、轴、轴,建立空间直角坐标系,则,.
.
易知平面的法向量.
设与平面所成角为,
则.
故选:C.
【变式2】(2023春·广东广州·高二执信中学校考阶段练习)如图,四棱锥中,平面,,,,为棱上一点.
(1)若为的中点,证明:平面;
(2)若,且平面,求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)取中点,连接和,
因为,,且为的中点,
所以且,
所以四边形为平行四边形,则,
因为平面,平面,
所以平面,
因为M,N分别为的中点,
所以,
因为平面,平面,
所以平面,
又因为平面,,
所以平面平面,
因为平面,
所以平面
(2)取中点,作交于,连接,
因为,所以,
因为平面,平面,
所以,
因为,
所以,
以为坐标原点,为正交基底建立如下图所示的空间直角坐标系,
、、、、.
所以,.
设平面的法向量,
又因为平面,
所以,
取,,,则.
又因为,
所以.
所以直线和平面所成角正弦值为.
【变式3】(2023春·福建宁德·高二校联考期中)在正四棱柱中,,,在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;
(2).
【详解】(1)在正四棱柱中,两两垂直,
以的方向为轴的正方向建立空间直角坐标系,如图,
则,,,,,,
,,,
于是,,即且,
而平面DBE,
所以平面DBE.
(2)由(1)得,为平面DBE的一个法向量,
因此,
所以直线与平面DBE所成角的正弦值为.
题型03易错题型利用向量法求直线与平面所成角的余弦值
(忽视最后正弦转余弦)
【典例1】(2023·高二单元测试)已知四棱柱的底面是边长为2的正方形,侧棱与底面垂直,若点到平面的距离为,则直线与平面所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】如图,连接交于点,过点作于,
则平面,则,
设,
则,
则根据三角形面积得,
代入解得.
以为坐标原点,建立如图所示的空间直角坐标系.
则,,
设平面的法向量为,,,
则,即,令,得.
,
所以直线与平面所成的角的余弦值为,
故选:.
【典例2】(2023春·甘肃金昌·高二永昌县第一高级中学校考期中)如图,已知平面,,,,,.若,,则与平面所成角的余弦值为__________.
【答案】
【详解】
依题意,以为坐标原点,分别以,,为轴、轴、轴的正方向,如图建立空间直角坐标系,
由已知可得,,,,,,
则,,.
设是平面的法向量,
则,即,
令,则,,
所以是平面的一个法向量.
设与平面所成的角为,.
因为,,,
则,
所以.
因为,
所以,
所以与平面所成角的余弦值为.
故答案为:.
【典例3】(2023春·江苏南京·高二南京市第五高级中学校考期中)如图,在底面为矩形的四棱锥中,平面平面.
(1)证明:;
(2)若,,设为中点,求直线与平面所成角的余弦值.
【答案】(1)证明见解析;(2)
【详解】(1)依题意,面面,,
∵面,面面,
∴面.
又面,
∴.
(2)解法一:向量法
在中,取中点,∵,
∴,∴面,
以为坐标原点,分别以为轴,过点且平行于的直线为轴,所在的直线为轴,建立如图空间直角坐标系,
设,∵,∴,
∴,,,,,
∴,,.
设面法向量为,
则,解得.
设直线与平面所成角为,
则,
因为,∴.
所以直线与平面所成角的余弦值为.
(2)解法二:几何法
过作交于点,则为中点,
过作的平行线,过作的平行线,交点为,连结,
过作交于点,连结,
连结,取中点,连结,,
四边形为矩形,所以面,所以,
又,所以面,
所以为线与面所成的角.
令,则,,,
由同一个三角形面积相等可得,
为直角三角形,由勾股定理可得,
所以,
又因为为锐角,所以,
所以直线与平面所成角的余弦值为.
【变式1】(2023·全国·高三对口高考)正三棱柱的所有棱长都相等,则和平面所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】设三棱柱的棱长为1,以B为原点,以过B作的垂线为x轴,以为轴,
建立空间直角坐标系,如图,
则,∴,
平面的一个法向量可取为,
设与平面所成的角为θ,,
则,
所以.
故选:A.
【变式2】(2023春·高二课时练习)若正三棱柱的所有棱长都相等,是的中点,则直线与平面所成角的余弦值为______.
【答案】/0.6
【详解】
如图,取中点,连接,
则有,
所以以为轴正方向建系如图,设,
则,
设平面的法向量为,
则有,令则,
所以,
设直线与平面所成角为,
则,
因为,所以
故答案为: .
【变式3】(2023·福建莆田·校考模拟预测)如图,在三棱锥中,,,,.
(1)证明:平面;
(2)求直线与平面所成角的余弦值.
【答案】(1)证明见解析
(2)
【详解】(1)证明:,,,,
,,,
,,
,、平面, 平面,
平面,,
因为,、平面,平面.
(2)解:因为,平面,以点为坐标原点,、、的方向分别为、、轴的
正方向建立如下图所示的空间直角坐标系,
则、、、,
,,
设平面的一个法向量分别为,
则,取,可得,
,,
设直线与平面所成角的,则,,
直线与平面所成角的余弦值.
题型04求直线与平面所成角(最值或范围)
【典例1】(2023春·高二课时练习)四棱锥,平面,底面是菱形,,平面平面.
(1)证明:⊥;
(2)设为上的点,求与平面所成角的正弦值的最大值.
【答案】(1)证明过程见解析
(2)
【详解】(1)如图,过点A作AE⊥PB于点E,
因为平面平面PBC,交线为PB,且AE平面PAB,
所以AE⊥平面PBC,
因为平面PBC,
所以AE⊥BC,
因为平面ABCD,平面ABCD,
所以PA⊥BC,
因为,平面PAB,
所以BC⊥平面PAB,
因为AB平面PAB,
所以BC⊥AB;
(2)因为底面ABCD是菱形,且BC⊥AB,
所以四边形ABCD为正方形,
以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
设AB=1,则,
,
设,,
则,
设平面ABM的法向量为,
则,
解得:,不妨令,则,
故,
设PC与平面ABM所成角大小为,
则,
,
当时,取得最大值,最大值为,
所以PC与平面ABM所成角的正弦值的最大值为.
【典例2】(2023·山东·校联考模拟预测)如图,圆锥的底面上有四点,且圆弧,点在线段上,若.
(1)证明:平面;
(2)若为等边三角形,点在劣弧上运动,记与平面所成的角为,求的最小值.
【答案】(1)证明见解析
(2).
【详解】(1)∵,∴为等边三角形,
所以为底面圆的直径,设,
在中,,,
所以则,
,
设到底面的距离分别为,
即,
即,所以即.
设的交点为,所以,即,
连接,则,面面,
所以面.
(2)设底面圆的圆心为,过作,
以为坐标原点,的方向为轴建立空间直角坐标系,
因为,所以由可得:,
设,则,
设平面的一个法向量为
∴,所以可取
∴
当且仅当,即与重合时取等号.
所以的最小值为.
【典例3】(2023春·湖南长沙·高三长沙一中校考阶段练习)如图,在长方体中,点是长方形内一点,是二面角的平面角.
(1)证明:点在上;
(2)若,求直线与平面所成角的正弦的最大值.
【答案】(1)证明见解析
(2)
【详解】(1)由是二面角的平面角,则,
又,面,则面,
又面,即,由长方体性质知,故,
由长方体性质:面,又面,则,
又,面,故面,
而面面,且面、面,根据过AC作与PD1垂直的平面有且仅有一个,
所以面与面为同一平面,又面,面面,
所以点在上;
(2)构建如下图示的空间直角坐标系,令,,
由题设,长方体上下底面都为正方形,由(1)知,则为中点,
所以且,,,
则,,,
若是面的一个法向量,则,令,则,
所以,
仅当时等号成立,故直线与平面所成角的正弦的最大值为.
【变式1】(2023春·江苏常州·高二江苏省溧阳中学校考阶段练习)如图,四棱锥的底面为正方形,底面,,点在棱上,且,点是棱上的动点(不含端点).
(1)若是棱的中点,求的余弦值;
(2)求与平面所成角的正弦值的最大值.
【答案】(1)
(2)
【详解】(1)由平面,,平面,所以,,
又,所以、、两两垂直,
以为坐标原点,分别以,,所在直线为,,轴,建立空间直角坐标系,
则,,,,,,
当为棱的中点时,,则,,
,
所以的余弦值为.
(2),设,,
则,则,又,
设平面的一个法向量为,
则,即,取,
,设与平面所成角为,
,
令,当时,,
即时,有最大值,
所以与平面所成角的正弦值的最大值为.
【变式2】(2023春·上海杨浦·高二上海市控江中学校考阶段练习)如图,在中,,,,可以通过以直线为轴旋转得到,且二面角是直二面角.动点在线段上.
(1)当为的中点时,求异面直线与所成角的余弦值;
(2)求与平面所成角的正弦最大值.
【答案】(1)(2)
【详解】(1)由题意可得:,平面平面,
平面平面,平面,
所以平面,
如图,以为坐标原点建立空间直角坐标系,则,
若为的中点,则,
可得,
设异面直线与所成角,
则.
故异面直线与所成角的余弦值为.
(2)若动点在线段上,设,
则,可得,解得,
即,则,
由题意可知:平面的法向量为,
设与平面所成角为,
则,
对于开口向上,对称轴为,
可得当时,取到最小值,
所以的最大值为,
题型05已知直线与平面所成角求参数
【典例1】(2023春·江苏连云港·高二校考期中)如图所示空间直角坐标系中,是正三棱柱的底面内一动点,,直线和底面所成角为,则点坐标满足( )
A. B. C.D.
【答案】A
【详解】解:由正三棱柱,且,根据坐标系可得:
,又是正三棱柱的底面内一动点,则,所以,
又平面,所以是平面的一个法向量,
因为直线和底面所成角为,
所以,
整理得,又,所以.
故选:A.
【典例2】(2023·全国·高三专题练习)在三棱锥中,,,互相垂直,,是线段上一动点,且直线与平面所成角的正切值的最大值是,则三棱锥外接球的体积是( )
A. B. C. D.
【答案】D
【详解】M是线段BC上一动点,连接PM.因为PA,PB,PC互相垂直,所以是直线AM与平面PBC所成的角.当PM最短,即时,直线AM与平面PBC所成角的正切值最大,此时,.
在中,,则,解得.
将三棱锥扩充为长方体,则长方体的体对角线长为.
故三棱锥外接球的半径,三棱锥外接球的体积为.所以D正确;
故选:D.
【典例3】(2023秋·重庆永川·高二重庆市永川北山中学校校考期末)如图,菱形中,,与相交于点,平面,,,.若直线与平面所成的角为45°,则=________.
【答案】2
【详解】设AE=a,在菱形ABCD中,∠ABC=60°,则△ABC为正三角形,又AB=2,易得OA=1,OB=,
如图,以O为坐标原点,以OA,OB所在直线分别为x轴、y轴,以过点O且平行于CF的直线为z轴建立空间直角坐标系.
则,
所以,设平面BED的法向量为,则,令z=1则,,
因为直线OF与平面BED所成角的大小为45°,
所以,
易知a>0,解得:a=2,所以AE=2.
故答案为:2.
【变式1】(2023·新疆喀什·统考模拟预测)如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为( )
A.1 B.2 C.3 D.4
【答案】D
【详解】以为原点,以,,为坐标轴建立空间坐标系如图所示,
设,则,,,
故,,,
设平面的一个法向量为,
则,可取,
故,
又直线与平面所成角的正弦值为,
,解得.
故选:D
【变式2】(2022·全国·高三专题练习)已知四面体中,,,两两垂直,,与平面所成角的正切值为,则点到平面的距离为( )
A. B. C. D.
【答案】D
【详解】以为原点,,,分别为,,轴建立空间直角坐标系,如图所示:
设,,,,,.
,,.
设平面的法向量,
则,令,得,,
故.
因为直线与平面所成角的正切值为,
所以直线与平面所成角的正弦值为.
即,解得.
所以平面的法向量,
故到平面的距离为.
故选:D
【变式3】(2022秋·内蒙古赤峰·高二赤峰二中校考期末)已知几何体如图所示,其中四边形,,均为正方形,且边长为1,点在上,若直线与平面所成的角为45°,则___________.
【答案】/
【详解】把该几何体补成一个正方体,如图,,连接,
由平面,平面,得,同理,.
又正方形中,,,平面,
所以平面,而平面,所以平面平面,
所以平面内的直线在平面上的射影是,即是直线MB与平面BEF所成的角,,
,
.
,.
故答案为:.
题型06直线与平面所成角中的探索性问题
【典例1】(2023春·云南·高三云南师大附中校考阶段练习)如图,平行六面体的所有棱长都相等,,,为棱的中点,在棱上运动,.
(1)证明:当时,平面;
(2)是否存在点,使得直线与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在,.
【详解】(1)证明:当时,为棱中点,
取中点为,连接,如图所示,
则,,
又因为,,
所以,
所以为平行四边形,
所以,
又因为平面,平面,
所以平面.
(2)存在当时,直线与平面所成角的正弦值为,理由如下:
不妨设棱长,则,
在中,,
所以,
同理可得,,
所以,
所以,
所以,
又因为在等边中,,
所以,
所以,
又因为,
所以以为原点,分别以、、为x轴、y轴、z轴建立空间直角坐标系如图所示,
则,,,,,,
则,,
所以,,
所以,,,
设平面的一个法向量为,
则,解得,
设直线与平面所成角为,
则,
解得(舍)或.
所以存在,直线与平面所成角的正弦值为.
【典例2】(2023春·江苏连云港·高二校考期中)如图,在三棱柱中,平面,,是的中点.
(1)求平面与平面夹角的余弦值;
(2)在直线上是否存在一点,使得与平面所成角的正弦值为,若存在,求出CP的长;若不存在,请说明理由.
【答案】(1)
(2)存在,或.
【详解】(1)因为平面ABC,平面ABC,则,,
以点C为坐标原点,建立空间直角坐标系,如图所示,
则,
所以平面ABC的一个法向量为,
设平面的法向量为,而,
所以,即,令,则,故,
所以,又平面与平面ABC夹角为锐角,
所以平面与平面ABC夹角的余弦值为;
(2)假设存在点P,
设,,
设BP与平面所成的角为,由(1)知,平面的法向量为,
则,
所以,解得或,
在线段CD上存在一点P,使BP与面所成角的正弦值为,此时或.
【变式1】(2023·福建漳州·统考模拟预测)如图,是圆的直径,点是圆上异于,的点,平面,,,,分别为,的中点,平面与平面的交线为,在圆上.
(1)在图中作出交线(说明画法,不必证明),并求三棱锥的体积;
(2)若点满足,且与平面所成角的正弦值为,求的值.
【答案】(1)答案见解析,
(2)或
【详解】(1)过点作交圆于点,( ,分别为,的中点,所以,又,所以,故为平面与平面的交线)
因为是圆的直径,所以,,
所以,所以四边形为矩形,
因为,,所以,
因为平面,为的中点,
所以点到平面的距离为,
所以
(2)以为坐标原点,分别以,,的方向作为轴,轴,轴的正方向建立空间直角坐标系,如图,
则,,,,,
所以,,,
,
设平面的法向量为,则
即,不妨取,得
因为与平面所成角的正弦值为,
所以
所以,所以或
【变式2】(2023·上海浦东新·华师大二附中校考三模)如图,直角三角形和等边三角形所在平面互相垂直,,是线段上一点.
令,则,.于是.
因为直线和平面所成角的正弦值为,
所以,
整理得,
解得或.
因为,
所以,即.
21世纪教育网(www.21cnjy.com)
