人教A版数学(选择性必修一讲义)第12讲第一章空间向量与立体几何测评卷(基础卷)(学生版+解析)
文档属性
| 名称 | 人教A版数学(选择性必修一讲义)第12讲第一章空间向量与立体几何测评卷(基础卷)(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 09:56:15 | ||
图片预览




文档简介
第一章 空间向量与立体几何 章节验收测评卷(基础卷)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(2023春·江苏徐州·高二统考期中)已知,,且,则x的值为( )
A. B. C.6 D.-6
2.(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱中,E为棱的中点.设,,,则( )
A. B.
C. D.
3.(2023春·浙江杭州·高二学军中学校考阶段练习)如图,某圆锥的轴截面是等边三角形,点B是底面圆周上的一点,且,点M是的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
4.(2023秋·辽宁辽阳·高二校联考期末)向量在向量上的投影向量为( )
A. B. C. D.
5.(2023·江苏扬州·扬州中学校考模拟预测)定义两个向量与的向量积是一个向量,它的模,它的方向与和同时垂直,且以的顺序符合右手法则(如图),在棱长为2的正四面体中,则( )
A. B.. C. D.
6.(2023春·安徽池州·高二池州市第一中学校联考阶段练习)已知直线l的方向向量,平面α的法向量,平面β的法向量,若直线平面α,则直线l与平面β所成角的余弦值为( )
A. B. C. D.
7.(2023·湖北·模拟预测)如图所示的多面体是由底面为的长方体被截面所截得到的,其中,,,,则点到平面的距离为( )
A. B. C. D.
8.(2023春·高三统考阶段练习)重庆南滨路钟楼地处长江与嘉陵江交汇处,建筑通过欧式风格将巴渝文化和开埠文化结合,展示了重庆的悠久历史。如图所示,可以将南滨路钟楼看作一个长方体,四个侧面各有一个大钟,则从到这段时间内,相邻两面钟的分针所成角为的次数为( )
A. B. C. D.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.(2023春·高二课时练习)关于空间向量,以下说法不正确的是( )
A.向量,,若,则
B.若对空间中任意一点,有,则,,,四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点,,,,,则,,三点共线
10.(2023·湖北十堰·统考二模)《九章算术》中,将上、下底面为直角三角形的直三棱柱叫做堑堵,在如图所示的堑堵中,,则( ).
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
11.(2023春·福建莆田·高二莆田第十中学校考阶段练习)已知空间向量,则( )
A. B.是共面向量
C. D.
12.(2023春·广东广州·高二广东番禺中学校考期中)如图,正方体的棱长为2,动点分别在线段上,则( )
A.异面直线和所成的角为
B.点到平面的距离为
C.若分别为线段的中点,则平面
D.线段长度的最小值为
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.(2023·高二校考课时练习)已知,,且与的夹角为钝角,则的取值范围是_________.
14.(2023秋·河南南阳·高二统考期末)如图,已知四棱柱的底面是边长为1的正方形,且,,则______.
15.(2023春·江苏徐州·高二统考期中)在直四棱柱中,底面是边长为2的正方形,.点是侧面内的动点(不含边界),,则与平面所成角的正切值的取值范围为__________.
16.(2023春·福建莆田·高二莆田华侨中学校考期中)在如图所示的三棱锥中,平面,,,,为中点,为内的动点(含边界),且.当在上时,________;点的轨迹的长度为________.
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明 证明过程或演算步骤.)
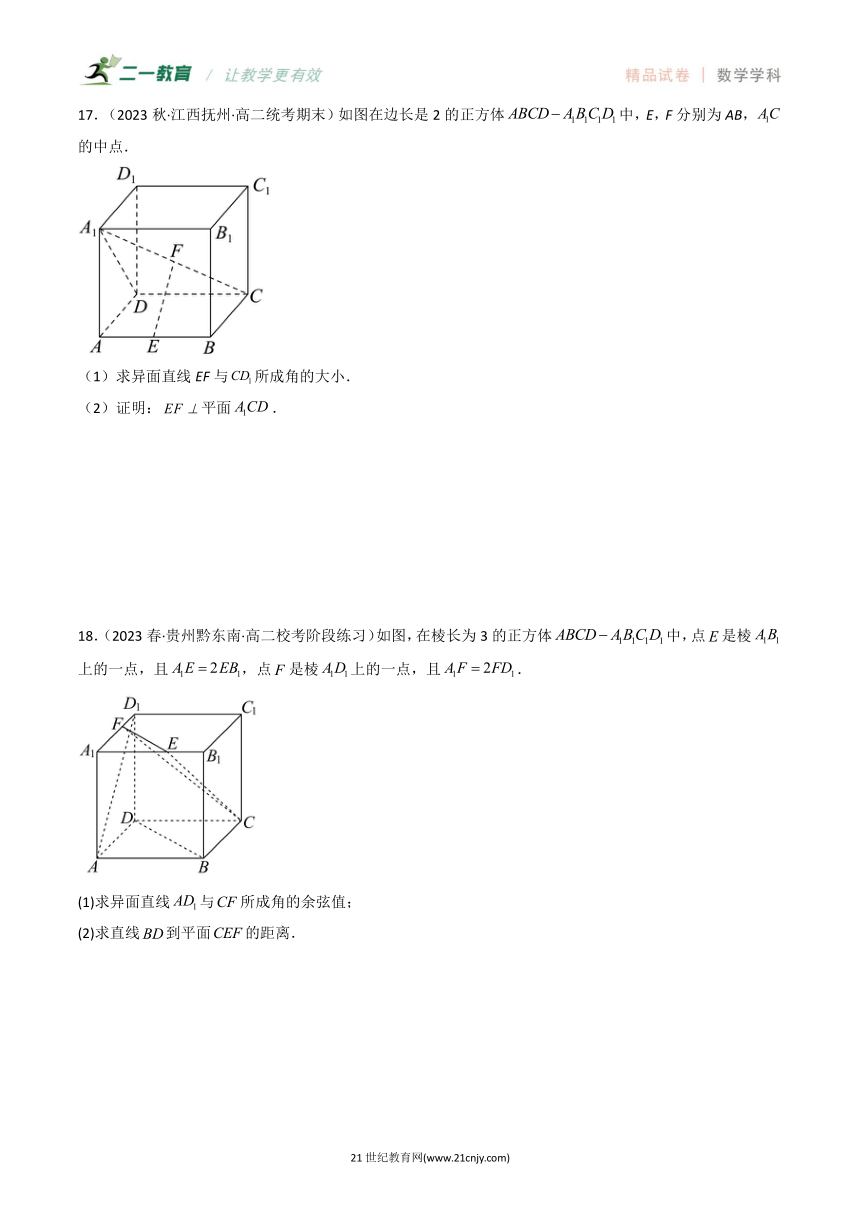
17.(2023秋·江西抚州·高二统考期末)如图在边长是2的正方体中,E,F分别为AB,的中点.
(1)求异面直线EF与所成角的大小.
(2)证明:平面.
18.(2023春·贵州黔东南·高二校考阶段练习)如图,在棱长为3的正方体中,点是棱上的一点,且,点是棱上的一点,且.
(1)求异面直线与所成角的余弦值;
(2)求直线到平面的距离.
19.(2023春·黑龙江鸡西·高二鸡西实验中学校考期中)如图所示,四棱锥的底面是矩形,底面,,,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
20.(2023·全国·高三专题练习)在斜三棱柱中,是等腰直角三角形,,平面底面,.
,.是棱上一点, 平面.
(1)求证:为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求四棱锥的体积.
条件 ①:点到平面的距离为;
条件 ②:直线与平面所成的角为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
第一章 空间向量与立体几何 章节验收测评卷(基础卷)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(2023春·江苏徐州·高二统考期中)已知,,且,则x的值为( )
A. B. C.6 D.-6
【答案】D
【详解】因为,所以,解得.
故选:D.
2.(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱中,E为棱的中点.设,,,则( )
A. B.
C. D.
【答案】A
【详解】由题意可得
.
故选:A.
3.(2023春·浙江杭州·高二学军中学校考阶段练习)如图,某圆锥的轴截面是等边三角形,点B是底面圆周上的一点,且,点M是的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
【答案】A
【详解】以过点O且垂直于平面的直线为x轴,直线分别为y轴,z轴,
建立如图所示的空间直角坐标系.不妨设,
则根据题意可得,
所以,
设异面直线与所成角为,
则.
故选:A.
4.(2023秋·辽宁辽阳·高二校联考期末)向量在向量上的投影向量为( )
A. B. C. D.
【答案】C
【详解】向量在向量上的投影向量为.
故选:C.
5.(2023·江苏扬州·扬州中学校考模拟预测)定义两个向量与的向量积是一个向量,它的模,它的方向与和同时垂直,且以的顺序符合右手法则(如图),在棱长为2的正四面体中,则( )
A. B.. C. D.
【答案】D
【详解】设,则,过作平面,则为三角形的外心,所以,进而
,
由于与共线,且方向相同,则
,
故选:D
6.(2023春·安徽池州·高二池州市第一中学校联考阶段练习)已知直线l的方向向量,平面α的法向量,平面β的法向量,若直线平面α,则直线l与平面β所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】依题意,,得,故;
而直线l与平面β所成角的正弦值,
故所求余弦值.
故选:A
7.(2023·湖北·模拟预测)如图所示的多面体是由底面为的长方体被截面所截得到的,其中,,,,则点到平面的距离为( )
A. B. C. D.
【答案】C
【详解】以D为原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz,
则,
∴,.
设为平面的法向量,,
由,得,
令z=1,∴,
所以.
又,
∴点C到平面AEC1F的距离d=.
故选:C.
8.(2023春·高三统考阶段练习)重庆南滨路钟楼地处长江与嘉陵江交汇处,建筑通过欧式风格将巴渝文化和开埠文化结合,展示了重庆的悠久历史。如图所示,可以将南滨路钟楼看作一个长方体,四个侧面各有一个大钟,则从到这段时间内,相邻两面钟的分针所成角为的次数为( )
A. B. C. D.
【答案】D
【详解】在长方体中,以点为坐标原点,,,所在直线分别为轴、轴、轴建立如图的空间直角坐标系.
设分针长为,矩形的对角线的交点为,矩形的对角线的交点为,
考察到这个时间段,
设时刻,侧面,内的钟的分针的针点的位置分别为,,
设,其中,则,,
由已知可得,则,
因为,故的取值为,,,,
即在到这个时间段,相邻两面钟的分针所成角为的次数为4,
因此,从到这段时间内,相邻两面钟的分针所成角为的次数为8.
故选:.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.(2023春·高二课时练习)关于空间向量,以下说法不正确的是( )
A.向量,,若,则
B.若对空间中任意一点,有,则,,,四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点,,,,,则,,三点共线
【答案】AC
【详解】对于A,向量,,若,若向量,均为非零向量,则由向量垂直的性质可得;若向量,其中一个为零向量,则与不垂直,故A错误;
对于B,若对空间中任意一点,有,
因为,所以,,,四点共面,故B正确;
对于C,设是空间中的一组基底,由向量的加法法则可知:,所以不能构成空间的一组基底,故C错误;
对于D,若空间四个点,,,,,由共线向量定理可知:,,三点共线,故D正确,
故选:.
10.(2023·湖北十堰·统考二模)《九章算术》中,将上、下底面为直角三角形的直三棱柱叫做堑堵,在如图所示的堑堵中,,则( ).
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
【答案】BD
【详解】因为
,故A不正确,B正确.
如图所示,故D作DU垂直BC,过U作VU垂直AB,UW垂直AC,
故向量在向量上的投影向量为,向量在向量上的投影向量为,
由题意易得故,C不正确. ,D正确.
故选:BD
11.(2023春·福建莆田·高二莆田第十中学校考阶段练习)已知空间向量,则( )
A. B.是共面向量
C. D.
【答案】ABC
【详解】,A项正确;
设,即,解得,,
即,所以,,共面,B项正确;
,所以,C项正确;
,D项错误.
故选:ABC.
12.(2023春·广东广州·高二广东番禺中学校考期中)如图,正方体的棱长为2,动点分别在线段上,则( )
A.异面直线和所成的角为
B.点到平面的距离为
C.若分别为线段的中点,则平面
D.线段长度的最小值为
【答案】BCD
【详解】因为,
所以异面直线和所成的角即为和所成的角,
因为,
所以为等边三角形,即,
故错误.
连接如图所示:
点到平面的距离为,
因为,
所以.
因为,
所以,
所以点到平面的距离为,
故B正确,
当分别为线段的中点时,
则为的中位线,
所以,
又平面,平面,
所以平面,
故C正确.
以为坐标原点,分别为轴建立空间直角坐标系,
如图所示:
则,
设,,
所以,
所以,
设,,
又
所以,
所以,
所以
当时,
有最小值,即,故D选项正确,
故选:BCD.
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.(2023·高二校考课时练习)已知,,且与的夹角为钝角,则的取值范围是_________.
【答案】
【详解】因为与的夹角为钝角,
,解得,
由题意得与不共线,则,解得,
的取值范围是.
故答案为:
14.(2023秋·河南南阳·高二统考期末)如图,已知四棱柱的底面是边长为1的正方形,且,,则______.
【答案】
【详解】设 ,,, 则 ,
底面是边长为1的正方形,且,,
则有,,,,,,
则 ,
所以.
故答案为:
15.(2023春·江苏徐州·高二统考期中)在直四棱柱中,底面是边长为2的正方形,.点是侧面内的动点(不含边界),,则与平面所成角的正切值的取值范围为__________.
【答案】
【详解】如图所示建立空间直角坐标系,
则,,设,得,,
由题意得,故,得,
故点轨迹是以为圆心,1为半径的圆在正方形内的部分,
由题可知为的中点,如图,
当共线时,取得最小值为,
而,
所以,
因为平面,所以与平面所成角即为,
所以,
故答案为:.
16.(2023春·福建莆田·高二莆田华侨中学校考期中)在如图所示的三棱锥中,平面,,,,为中点,为内的动点(含边界),且.当在上时,________;点的轨迹的长度为________.
【答案】
【详解】因为平面,平面,所以,又,所以,
又平面,所以平面,过,如图建立空间直角坐标系,
则,设,所以,则
①当在上时,设,因为,所以,故,则
所以;
②为内的动点(含边界)时,如图,取中点,过作,垂足为
由①可得,又,平面,所以平面,因为平面,所以
即在线段上运动时,,
点的轨迹为线段.
则.
故答案为:;.
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明 证明过程或演算步骤.)
17.(2023秋·江西抚州·高二统考期末)如图在边长是2的正方体中,E,F分别为AB,的中点.
(1)求异面直线EF与所成角的大小.
(2)证明:平面.
【答案】(1);(2)证明见解析.
【详解】据题意,建立如图坐标系.于是:
,,,,,
∴,,,.
(1),
∴
∴异面直线EF和所成的角为.
(2)
∴,即
,
∴即.
又∵,平面且
∴平面.
18.(2023春·贵州黔东南·高二校考阶段练习)如图,在棱长为3的正方体中,点是棱上的一点,且,点是棱上的一点,且.
(1)求异面直线与所成角的余弦值;
(2)求直线到平面的距离.
【答案】(1)
(2)
【详解】(1)建立如图所示的空间直角坐标系,
,
,
所以,
所以异面直线与所成角的余弦值为;
(2)连接,显然,因为, .
所以,于是,
因为平面,平面,
所以平面,
因此直线到平面的距离就是点到平面的距离,
设平面的法向量为,
,
则有,
,
点到平面的距离为:
.
19.(2023春·黑龙江鸡西·高二鸡西实验中学校考期中)如图所示,四棱锥的底面是矩形,底面,,,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)由题意知,,,两两互相垂直,以为原点,,,所在直线分别为轴,建立如图所示的空间直角坐标系,
则,,,,
所以,.
底面,底面,
又,,
且平面,
平面,
所以是平面的一个法向量.
因为,
所以.
又平面,所以平面.
(2)因为,,,,,
所以,,,
设平面的法向量为,则
由,解得,令,
得平面的一个法向量为.
设直线与平面所成的角为,
则.
故:直线与平面所成角的正弦值为.
20.(2023·全国·高三专题练习)在斜三棱柱中,是等腰直角三角形,,平面底面,.
(1)证明:;
(2)求二面角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)证明:取中点,连接,如图所示:
∵是等腰直角三角形,
∴,且,
∵平面底面,平面底面平面,
∴平面,
∵平面,
∴,
∵,
∴,
∴,(符合勾股定理),
∴,
∵平面,
∴平面,
∵平面,
∴.
(2)由(1)知,可以建立分别以为轴的空间直角坐标系,
则,
又因为斜三棱柱中,,
所以,
所以,
设平面的法向量,
则,令,则,
∴平面的法向量,
设平面的法向量,
则,令,则,
∴平面的法向量,
设二面角的平面角为,
则.
所以,
故二面角的正弦值为.
21.(2023·全国·高三对口高考)如图所示的几何体中,四边形是等腰梯形,,,平面,,.
(1)求二面角的余弦值;
(2)在线段AB(含端点)上,是否存在一点P,使得平面.若存在,求出的值;若不存在,请说明理由.
【答案】(1)
(2)存在,
【详解】(1)过作于,由于,则,由于,且四边形是等腰梯形,所以,在三角形中,由余弦定理可得,所以,故,
以为坐标原点,,为轴,轴,过点作的平行线为轴,建立空间直角坐标系,设,则,
设面的法向量,
则,即,取,得.
设面的法向量,
则,即,则取,得.
,
由几何体的特征可知二面角的平面角为锐角,
二面角的余弦值为.
(2),,, 面,
面.
设,
若平面,则 ,所以,
所以
22.(2023秋·北京·高三校考期末)如图,在四棱锥中,, ,,,,.是棱上一点, 平面.
(1)求证:为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求四棱锥的体积.
条件 ①:点到平面的距离为;
条件 ②:直线与平面所成的角为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)条件选择见解析,
【详解】(1)过点作交于点,连接,如图所示:
因为,所以 .
所以四点共面.
又因为平面 ,平面平面
所以
所以四边形是平行四边形
所以,
由,,
所以,所以
所以为的中位线,
所以为的中点.
(2)过作于,连接.
因为,又因为 ,
且,
所以 平面.
又平面,
所以 平面平面.
因为,所以为中点,
又因为平面平面,
所以平面.
又平面,
所以
如图建立空间直角坐标系.
21世纪教育网(www.21cnjy.com)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(2023春·江苏徐州·高二统考期中)已知,,且,则x的值为( )
A. B. C.6 D.-6
2.(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱中,E为棱的中点.设,,,则( )
A. B.
C. D.
3.(2023春·浙江杭州·高二学军中学校考阶段练习)如图,某圆锥的轴截面是等边三角形,点B是底面圆周上的一点,且,点M是的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
4.(2023秋·辽宁辽阳·高二校联考期末)向量在向量上的投影向量为( )
A. B. C. D.
5.(2023·江苏扬州·扬州中学校考模拟预测)定义两个向量与的向量积是一个向量,它的模,它的方向与和同时垂直,且以的顺序符合右手法则(如图),在棱长为2的正四面体中,则( )
A. B.. C. D.
6.(2023春·安徽池州·高二池州市第一中学校联考阶段练习)已知直线l的方向向量,平面α的法向量,平面β的法向量,若直线平面α,则直线l与平面β所成角的余弦值为( )
A. B. C. D.
7.(2023·湖北·模拟预测)如图所示的多面体是由底面为的长方体被截面所截得到的,其中,,,,则点到平面的距离为( )
A. B. C. D.
8.(2023春·高三统考阶段练习)重庆南滨路钟楼地处长江与嘉陵江交汇处,建筑通过欧式风格将巴渝文化和开埠文化结合,展示了重庆的悠久历史。如图所示,可以将南滨路钟楼看作一个长方体,四个侧面各有一个大钟,则从到这段时间内,相邻两面钟的分针所成角为的次数为( )
A. B. C. D.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.(2023春·高二课时练习)关于空间向量,以下说法不正确的是( )
A.向量,,若,则
B.若对空间中任意一点,有,则,,,四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点,,,,,则,,三点共线
10.(2023·湖北十堰·统考二模)《九章算术》中,将上、下底面为直角三角形的直三棱柱叫做堑堵,在如图所示的堑堵中,,则( ).
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
11.(2023春·福建莆田·高二莆田第十中学校考阶段练习)已知空间向量,则( )
A. B.是共面向量
C. D.
12.(2023春·广东广州·高二广东番禺中学校考期中)如图,正方体的棱长为2,动点分别在线段上,则( )
A.异面直线和所成的角为
B.点到平面的距离为
C.若分别为线段的中点,则平面
D.线段长度的最小值为
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.(2023·高二校考课时练习)已知,,且与的夹角为钝角,则的取值范围是_________.
14.(2023秋·河南南阳·高二统考期末)如图,已知四棱柱的底面是边长为1的正方形,且,,则______.
15.(2023春·江苏徐州·高二统考期中)在直四棱柱中,底面是边长为2的正方形,.点是侧面内的动点(不含边界),,则与平面所成角的正切值的取值范围为__________.
16.(2023春·福建莆田·高二莆田华侨中学校考期中)在如图所示的三棱锥中,平面,,,,为中点,为内的动点(含边界),且.当在上时,________;点的轨迹的长度为________.
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明 证明过程或演算步骤.)
17.(2023秋·江西抚州·高二统考期末)如图在边长是2的正方体中,E,F分别为AB,的中点.
(1)求异面直线EF与所成角的大小.
(2)证明:平面.
18.(2023春·贵州黔东南·高二校考阶段练习)如图,在棱长为3的正方体中,点是棱上的一点,且,点是棱上的一点,且.
(1)求异面直线与所成角的余弦值;
(2)求直线到平面的距离.
19.(2023春·黑龙江鸡西·高二鸡西实验中学校考期中)如图所示,四棱锥的底面是矩形,底面,,,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
20.(2023·全国·高三专题练习)在斜三棱柱中,是等腰直角三角形,,平面底面,.
,.是棱上一点, 平面.
(1)求证:为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求四棱锥的体积.
条件 ①:点到平面的距离为;
条件 ②:直线与平面所成的角为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
第一章 空间向量与立体几何 章节验收测评卷(基础卷)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(2023春·江苏徐州·高二统考期中)已知,,且,则x的值为( )
A. B. C.6 D.-6
【答案】D
【详解】因为,所以,解得.
故选:D.
2.(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱中,E为棱的中点.设,,,则( )
A. B.
C. D.
【答案】A
【详解】由题意可得
.
故选:A.
3.(2023春·浙江杭州·高二学军中学校考阶段练习)如图,某圆锥的轴截面是等边三角形,点B是底面圆周上的一点,且,点M是的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
【答案】A
【详解】以过点O且垂直于平面的直线为x轴,直线分别为y轴,z轴,
建立如图所示的空间直角坐标系.不妨设,
则根据题意可得,
所以,
设异面直线与所成角为,
则.
故选:A.
4.(2023秋·辽宁辽阳·高二校联考期末)向量在向量上的投影向量为( )
A. B. C. D.
【答案】C
【详解】向量在向量上的投影向量为.
故选:C.
5.(2023·江苏扬州·扬州中学校考模拟预测)定义两个向量与的向量积是一个向量,它的模,它的方向与和同时垂直,且以的顺序符合右手法则(如图),在棱长为2的正四面体中,则( )
A. B.. C. D.
【答案】D
【详解】设,则,过作平面,则为三角形的外心,所以,进而
,
由于与共线,且方向相同,则
,
故选:D
6.(2023春·安徽池州·高二池州市第一中学校联考阶段练习)已知直线l的方向向量,平面α的法向量,平面β的法向量,若直线平面α,则直线l与平面β所成角的余弦值为( )
A. B. C. D.
【答案】A
【详解】依题意,,得,故;
而直线l与平面β所成角的正弦值,
故所求余弦值.
故选:A
7.(2023·湖北·模拟预测)如图所示的多面体是由底面为的长方体被截面所截得到的,其中,,,,则点到平面的距离为( )
A. B. C. D.
【答案】C
【详解】以D为原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz,
则,
∴,.
设为平面的法向量,,
由,得,
令z=1,∴,
所以.
又,
∴点C到平面AEC1F的距离d=.
故选:C.
8.(2023春·高三统考阶段练习)重庆南滨路钟楼地处长江与嘉陵江交汇处,建筑通过欧式风格将巴渝文化和开埠文化结合,展示了重庆的悠久历史。如图所示,可以将南滨路钟楼看作一个长方体,四个侧面各有一个大钟,则从到这段时间内,相邻两面钟的分针所成角为的次数为( )
A. B. C. D.
【答案】D
【详解】在长方体中,以点为坐标原点,,,所在直线分别为轴、轴、轴建立如图的空间直角坐标系.
设分针长为,矩形的对角线的交点为,矩形的对角线的交点为,
考察到这个时间段,
设时刻,侧面,内的钟的分针的针点的位置分别为,,
设,其中,则,,
由已知可得,则,
因为,故的取值为,,,,
即在到这个时间段,相邻两面钟的分针所成角为的次数为4,
因此,从到这段时间内,相邻两面钟的分针所成角为的次数为8.
故选:.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.(2023春·高二课时练习)关于空间向量,以下说法不正确的是( )
A.向量,,若,则
B.若对空间中任意一点,有,则,,,四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点,,,,,则,,三点共线
【答案】AC
【详解】对于A,向量,,若,若向量,均为非零向量,则由向量垂直的性质可得;若向量,其中一个为零向量,则与不垂直,故A错误;
对于B,若对空间中任意一点,有,
因为,所以,,,四点共面,故B正确;
对于C,设是空间中的一组基底,由向量的加法法则可知:,所以不能构成空间的一组基底,故C错误;
对于D,若空间四个点,,,,,由共线向量定理可知:,,三点共线,故D正确,
故选:.
10.(2023·湖北十堰·统考二模)《九章算术》中,将上、下底面为直角三角形的直三棱柱叫做堑堵,在如图所示的堑堵中,,则( ).
A.
B.
C.向量在向量上的投影向量为
D.向量在向量上的投影向量为
【答案】BD
【详解】因为
,故A不正确,B正确.
如图所示,故D作DU垂直BC,过U作VU垂直AB,UW垂直AC,
故向量在向量上的投影向量为,向量在向量上的投影向量为,
由题意易得故,C不正确. ,D正确.
故选:BD
11.(2023春·福建莆田·高二莆田第十中学校考阶段练习)已知空间向量,则( )
A. B.是共面向量
C. D.
【答案】ABC
【详解】,A项正确;
设,即,解得,,
即,所以,,共面,B项正确;
,所以,C项正确;
,D项错误.
故选:ABC.
12.(2023春·广东广州·高二广东番禺中学校考期中)如图,正方体的棱长为2,动点分别在线段上,则( )
A.异面直线和所成的角为
B.点到平面的距离为
C.若分别为线段的中点,则平面
D.线段长度的最小值为
【答案】BCD
【详解】因为,
所以异面直线和所成的角即为和所成的角,
因为,
所以为等边三角形,即,
故错误.
连接如图所示:
点到平面的距离为,
因为,
所以.
因为,
所以,
所以点到平面的距离为,
故B正确,
当分别为线段的中点时,
则为的中位线,
所以,
又平面,平面,
所以平面,
故C正确.
以为坐标原点,分别为轴建立空间直角坐标系,
如图所示:
则,
设,,
所以,
所以,
设,,
又
所以,
所以,
所以
当时,
有最小值,即,故D选项正确,
故选:BCD.
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.(2023·高二校考课时练习)已知,,且与的夹角为钝角,则的取值范围是_________.
【答案】
【详解】因为与的夹角为钝角,
,解得,
由题意得与不共线,则,解得,
的取值范围是.
故答案为:
14.(2023秋·河南南阳·高二统考期末)如图,已知四棱柱的底面是边长为1的正方形,且,,则______.
【答案】
【详解】设 ,,, 则 ,
底面是边长为1的正方形,且,,
则有,,,,,,
则 ,
所以.
故答案为:
15.(2023春·江苏徐州·高二统考期中)在直四棱柱中,底面是边长为2的正方形,.点是侧面内的动点(不含边界),,则与平面所成角的正切值的取值范围为__________.
【答案】
【详解】如图所示建立空间直角坐标系,
则,,设,得,,
由题意得,故,得,
故点轨迹是以为圆心,1为半径的圆在正方形内的部分,
由题可知为的中点,如图,
当共线时,取得最小值为,
而,
所以,
因为平面,所以与平面所成角即为,
所以,
故答案为:.
16.(2023春·福建莆田·高二莆田华侨中学校考期中)在如图所示的三棱锥中,平面,,,,为中点,为内的动点(含边界),且.当在上时,________;点的轨迹的长度为________.
【答案】
【详解】因为平面,平面,所以,又,所以,
又平面,所以平面,过,如图建立空间直角坐标系,
则,设,所以,则
①当在上时,设,因为,所以,故,则
所以;
②为内的动点(含边界)时,如图,取中点,过作,垂足为
由①可得,又,平面,所以平面,因为平面,所以
即在线段上运动时,,
点的轨迹为线段.
则.
故答案为:;.
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明 证明过程或演算步骤.)
17.(2023秋·江西抚州·高二统考期末)如图在边长是2的正方体中,E,F分别为AB,的中点.
(1)求异面直线EF与所成角的大小.
(2)证明:平面.
【答案】(1);(2)证明见解析.
【详解】据题意,建立如图坐标系.于是:
,,,,,
∴,,,.
(1),
∴
∴异面直线EF和所成的角为.
(2)
∴,即
,
∴即.
又∵,平面且
∴平面.
18.(2023春·贵州黔东南·高二校考阶段练习)如图,在棱长为3的正方体中,点是棱上的一点,且,点是棱上的一点,且.
(1)求异面直线与所成角的余弦值;
(2)求直线到平面的距离.
【答案】(1)
(2)
【详解】(1)建立如图所示的空间直角坐标系,
,
,
所以,
所以异面直线与所成角的余弦值为;
(2)连接,显然,因为, .
所以,于是,
因为平面,平面,
所以平面,
因此直线到平面的距离就是点到平面的距离,
设平面的法向量为,
,
则有,
,
点到平面的距离为:
.
19.(2023春·黑龙江鸡西·高二鸡西实验中学校考期中)如图所示,四棱锥的底面是矩形,底面,,,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)由题意知,,,两两互相垂直,以为原点,,,所在直线分别为轴,建立如图所示的空间直角坐标系,
则,,,,
所以,.
底面,底面,
又,,
且平面,
平面,
所以是平面的一个法向量.
因为,
所以.
又平面,所以平面.
(2)因为,,,,,
所以,,,
设平面的法向量为,则
由,解得,令,
得平面的一个法向量为.
设直线与平面所成的角为,
则.
故:直线与平面所成角的正弦值为.
20.(2023·全国·高三专题练习)在斜三棱柱中,是等腰直角三角形,,平面底面,.
(1)证明:;
(2)求二面角的正弦值.
【答案】(1)证明见解析
(2)
【详解】(1)证明:取中点,连接,如图所示:
∵是等腰直角三角形,
∴,且,
∵平面底面,平面底面平面,
∴平面,
∵平面,
∴,
∵,
∴,
∴,(符合勾股定理),
∴,
∵平面,
∴平面,
∵平面,
∴.
(2)由(1)知,可以建立分别以为轴的空间直角坐标系,
则,
又因为斜三棱柱中,,
所以,
所以,
设平面的法向量,
则,令,则,
∴平面的法向量,
设平面的法向量,
则,令,则,
∴平面的法向量,
设二面角的平面角为,
则.
所以,
故二面角的正弦值为.
21.(2023·全国·高三对口高考)如图所示的几何体中,四边形是等腰梯形,,,平面,,.
(1)求二面角的余弦值;
(2)在线段AB(含端点)上,是否存在一点P,使得平面.若存在,求出的值;若不存在,请说明理由.
【答案】(1)
(2)存在,
【详解】(1)过作于,由于,则,由于,且四边形是等腰梯形,所以,在三角形中,由余弦定理可得,所以,故,
以为坐标原点,,为轴,轴,过点作的平行线为轴,建立空间直角坐标系,设,则,
设面的法向量,
则,即,取,得.
设面的法向量,
则,即,则取,得.
,
由几何体的特征可知二面角的平面角为锐角,
二面角的余弦值为.
(2),,, 面,
面.
设,
若平面,则 ,所以,
所以
22.(2023秋·北京·高三校考期末)如图,在四棱锥中,, ,,,,.是棱上一点, 平面.
(1)求证:为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求四棱锥的体积.
条件 ①:点到平面的距离为;
条件 ②:直线与平面所成的角为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)条件选择见解析,
【详解】(1)过点作交于点,连接,如图所示:
因为,所以 .
所以四点共面.
又因为平面 ,平面平面
所以
所以四边形是平行四边形
所以,
由,,
所以,所以
所以为的中位线,
所以为的中点.
(2)过作于,连接.
因为,又因为 ,
且,
所以 平面.
又平面,
所以 平面平面.
因为,所以为中点,
又因为平面平面,
所以平面.
又平面,
所以
如图建立空间直角坐标系.
21世纪教育网(www.21cnjy.com)
