山东省滨州市邹平市青阳镇初中2024-2025学年第一学期期中八年级数学测试题A卷(pdf版,无答案)
文档属性
| 名称 | 山东省滨州市邹平市青阳镇初中2024-2025学年第一学期期中八年级数学测试题A卷(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 293.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 15:00:21 | ||
图片预览



文档简介
2024—2025学年第一学期期中学业检测
八年级数学试题(A卷)
温馨提示:
1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 8页。满分 120分。考试用时 120分钟。
2.答卷前,考生务必用 0.5 毫米黑色签字笔将自己的学校、姓名、准考证号填写
在答题卡中规定的位置上。
3.第Ⅰ卷每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑;如需
改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4. 第Ⅱ卷必须用 0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域
内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答
案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第 Ⅰ 卷(选择题 共 30分)
一、选择题(本题共 10个小题,在每小题的四个选项中只有一个是正确的,请把正确的选
项选出来,每小题 3分,满分 30分)
1.第 33届夏季奥运会于 2024年 7月 26日至 8月 11日在法国巴黎举行,中国取得金牌
榜第一名的好成绩,如图所示巴黎奥运会项目图标中,是轴对称图形的是
A. B. C. D.
2.已知三角形两边长分别为 3和 5,则第三边的长可能是
A.2 B.6 C.8 D.9
3.如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是
A.∠M=∠N B.AM∥CN C.AB=CD D.AM=CN
4.如图,在 Rt△ABC中,∠A=90°,在 AB的延长线上取点 D,过点 D作 DE∥BC.若
∠C=38°,则∠D的度数为
八年级数学试题 A卷 第 1 页 (共 8 页)
A.38° B.42° C.52° D.62°
5.观察图中尺规作图的痕迹,可得线段 BD一定是△ABC的
A.角平分线 B.高线 C.中位线 D.中线
6.已知图中的两个三角形全等,则∠1的度数是
A.76° B.64° C.60° D.50°
7.如图,点 D在线段 BC上.若 BC=DE,AC=DC,
AB=EC,∠A=95°,∠ACB=55°,则∠ACE=
A.30° B.40° C.50° D.55°
8.下列推理中,不能判断△ABC是等边三角形的是
A.∠A=∠B=∠C B.AB=AC,∠B=60°
C.∠A=60°,∠B=60° D.AB=AC,且∠B=∠C
9.如图,BC=13cm,∠B=∠BAC=15°,AD⊥BC于点 D,
则 AD的长为
A.5.5cm B.5cm
C.6cm D.6.5cm
10.如图,点 A在 x轴的正半轴上,坐标为(4,0),点
B在 y 轴的正半轴上,且 PA=PB,点 P 是∠AOB 的平分
线上的点,且横坐标为 3,则点 B的坐标为
A.(0,2) B.(2,0)
C.(1,0) D.(0,1)
八年级数学试题 A卷 第 2 页 (共 8 页)
第 Ⅱ 卷(非选择题 共 90分)
二、填空题(每小题 3分,共计 18分)
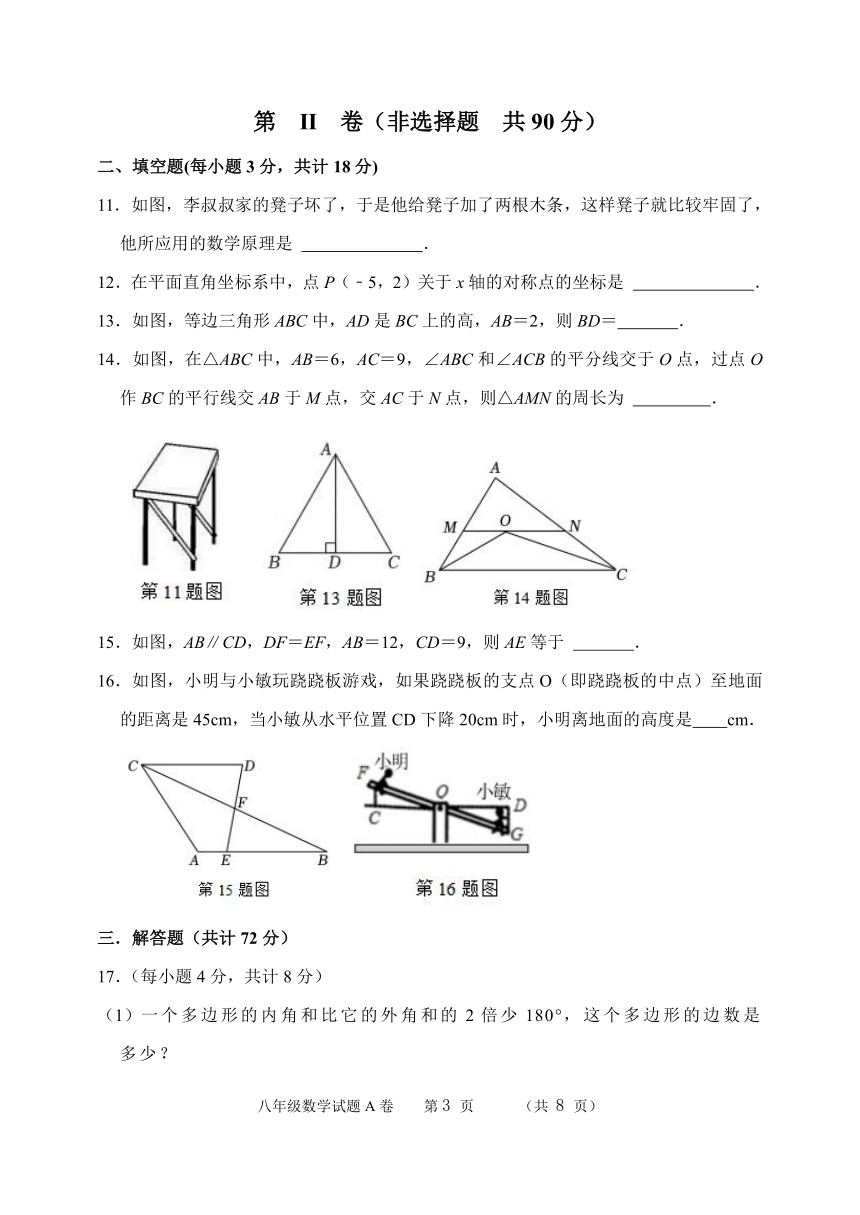
11.如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,
他所应用的数学原理是 .
12.在平面直角坐标系中,点 P(﹣5,2)关于 x轴的对称点的坐标是 .
13.如图,等边三角形 ABC中,AD是 BC上的高,AB=2,则 BD= .
14.如图,在△ABC中,AB=6,AC=9,∠ABC和∠ACB的平分线交于 O点,过点 O
作 BC的平行线交 AB于 M点,交 AC于 N点,则△AMN的周长为 .
15.如图,AB∥CD,DF=EF,AB=12,CD=9,则 AE等于 .
16.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点 O(即跷跷板的中点)至地面
的距离是 45cm,当小敏从水平位置 CD下降 20cm时,小明离地面的高度是 cm.
三.解答题(共计 72分)
17.(每小题 4分,共计 8分)
(1)一个多边形的内角和比它的外角和的 2 倍少 180°,这个多边形的边数是
多少?
八年级数学试题 A卷 第 3 页 (共 8 页)
(2)如图,已知∠A=∠D=90°,E、F在线段 BC上,DE与 AF交于点 O,且 AB=DC,
BE=CF.求证:∠B=∠C.
18.(每小题 4分,共计 8分)(1)小红在求一个凸 n边形的内角和时,多算了一个角,
求得的内角和为 1920°.多算进去的那个内角为多少度?
(2)已知一个三角形的两条边长分别为 4cm,8cm.设第三条边长为 xcm.
若此三角形为等腰三角形,求该等腰三角形的周长.
19.(8分)如图,在平面直角坐标系中,△ABC的顶点坐标 A(﹣1,5),B(﹣1,0),
C(﹣4,3).
(1)请在图中画出△ABC关于 y轴对称的图形△A1B1C1(其中 A1,B1,C1分别是 A,B,
C的对应点,不写画法);并写出点 C1的坐标.
(2)在 y轴上画出点 P,使得 PA+PB最小.
八年级数学试题 A卷 第 4 页 (共 8 页)
20.(8分)如图,AB=AC,AB的垂直平分线交 AC于 D,交 AB于 E.
(1)若∠A=40°,求∠DBC的度数;
(2)若 AE=5,△BCD的周长 17,求△ABC的周长.
21.(8分)如图,AD是△ABC的 BC边上的高,AE平分∠BAC,若∠B=42°,∠C=
70°,求∠AEC和∠DAE的度数.
八年级数学试题 A卷 第 5 页 (共 8 页)
22.(10分)某段河流的两岸是平行的,某数学兴趣小组在老师的带领下不用涉水过河就
能测得河的宽度,他们是这样做的:
①在河流的岸边点 B处,选对岸正对的一棵树 A;
②沿河岸直行 15m处有一棵树 C,继续前行 15m到达点 D处;
③从点 D处沿河岸垂直的方向行走,当到达 A树正好被 C树遮挡住的点 E处时,停止行
走;
④测得 DE的长为 10m.
(1)请你判断他们做法的正确性并说明理由;
(2)河的宽度是多少米?
八年级数学试题 A卷 第 6 页 (共 8 页)
23.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点 O,且 OD∥AB
交 BC于点 D,OE∥AC交 BC于点.
(1)试判定△ODE的形状,并说明你的理由;
(2)若 BC=10,求△ODE的周长.
八年级数学试题 A卷 第 7 页 (共 8 页)
24.(12分)综合与实践:数学模型可以用来解决一类问题,是数学应用基本途径.通过
探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经
验,并将其运用到更广阔的数学天地.
(1)发现问题:如图 1,在△ABC 和△AEF 中,AB=AC,AE=AF,∠BAC=∠EAF
=30°,连接 BE,CF,延长 BE交 CF于点 D.则 BE与 CF的数量关系: ,
∠BDC= °;
(2)类比探究:如图 2,在△ABC 和△AEF 中,AB=AC,AE=AF,∠BAC=∠EAF
=120°,连接 BE,CF,延长 BE,FC交于点 D.请猜想 BE与 CF的数量关系及∠BDC
的度数,并说明理由.
八年级数学试题 A卷 第 8 页 (共 8 页)
八年级数学试题(A卷)
温馨提示:
1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 8页。满分 120分。考试用时 120分钟。
2.答卷前,考生务必用 0.5 毫米黑色签字笔将自己的学校、姓名、准考证号填写
在答题卡中规定的位置上。
3.第Ⅰ卷每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑;如需
改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4. 第Ⅱ卷必须用 0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域
内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答
案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第 Ⅰ 卷(选择题 共 30分)
一、选择题(本题共 10个小题,在每小题的四个选项中只有一个是正确的,请把正确的选
项选出来,每小题 3分,满分 30分)
1.第 33届夏季奥运会于 2024年 7月 26日至 8月 11日在法国巴黎举行,中国取得金牌
榜第一名的好成绩,如图所示巴黎奥运会项目图标中,是轴对称图形的是
A. B. C. D.
2.已知三角形两边长分别为 3和 5,则第三边的长可能是
A.2 B.6 C.8 D.9
3.如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是
A.∠M=∠N B.AM∥CN C.AB=CD D.AM=CN
4.如图,在 Rt△ABC中,∠A=90°,在 AB的延长线上取点 D,过点 D作 DE∥BC.若
∠C=38°,则∠D的度数为
八年级数学试题 A卷 第 1 页 (共 8 页)
A.38° B.42° C.52° D.62°
5.观察图中尺规作图的痕迹,可得线段 BD一定是△ABC的
A.角平分线 B.高线 C.中位线 D.中线
6.已知图中的两个三角形全等,则∠1的度数是
A.76° B.64° C.60° D.50°
7.如图,点 D在线段 BC上.若 BC=DE,AC=DC,
AB=EC,∠A=95°,∠ACB=55°,则∠ACE=
A.30° B.40° C.50° D.55°
8.下列推理中,不能判断△ABC是等边三角形的是
A.∠A=∠B=∠C B.AB=AC,∠B=60°
C.∠A=60°,∠B=60° D.AB=AC,且∠B=∠C
9.如图,BC=13cm,∠B=∠BAC=15°,AD⊥BC于点 D,
则 AD的长为
A.5.5cm B.5cm
C.6cm D.6.5cm
10.如图,点 A在 x轴的正半轴上,坐标为(4,0),点
B在 y 轴的正半轴上,且 PA=PB,点 P 是∠AOB 的平分
线上的点,且横坐标为 3,则点 B的坐标为
A.(0,2) B.(2,0)
C.(1,0) D.(0,1)
八年级数学试题 A卷 第 2 页 (共 8 页)
第 Ⅱ 卷(非选择题 共 90分)
二、填空题(每小题 3分,共计 18分)
11.如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,
他所应用的数学原理是 .
12.在平面直角坐标系中,点 P(﹣5,2)关于 x轴的对称点的坐标是 .
13.如图,等边三角形 ABC中,AD是 BC上的高,AB=2,则 BD= .
14.如图,在△ABC中,AB=6,AC=9,∠ABC和∠ACB的平分线交于 O点,过点 O
作 BC的平行线交 AB于 M点,交 AC于 N点,则△AMN的周长为 .
15.如图,AB∥CD,DF=EF,AB=12,CD=9,则 AE等于 .
16.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点 O(即跷跷板的中点)至地面
的距离是 45cm,当小敏从水平位置 CD下降 20cm时,小明离地面的高度是 cm.
三.解答题(共计 72分)
17.(每小题 4分,共计 8分)
(1)一个多边形的内角和比它的外角和的 2 倍少 180°,这个多边形的边数是
多少?
八年级数学试题 A卷 第 3 页 (共 8 页)
(2)如图,已知∠A=∠D=90°,E、F在线段 BC上,DE与 AF交于点 O,且 AB=DC,
BE=CF.求证:∠B=∠C.
18.(每小题 4分,共计 8分)(1)小红在求一个凸 n边形的内角和时,多算了一个角,
求得的内角和为 1920°.多算进去的那个内角为多少度?
(2)已知一个三角形的两条边长分别为 4cm,8cm.设第三条边长为 xcm.
若此三角形为等腰三角形,求该等腰三角形的周长.
19.(8分)如图,在平面直角坐标系中,△ABC的顶点坐标 A(﹣1,5),B(﹣1,0),
C(﹣4,3).
(1)请在图中画出△ABC关于 y轴对称的图形△A1B1C1(其中 A1,B1,C1分别是 A,B,
C的对应点,不写画法);并写出点 C1的坐标.
(2)在 y轴上画出点 P,使得 PA+PB最小.
八年级数学试题 A卷 第 4 页 (共 8 页)
20.(8分)如图,AB=AC,AB的垂直平分线交 AC于 D,交 AB于 E.
(1)若∠A=40°,求∠DBC的度数;
(2)若 AE=5,△BCD的周长 17,求△ABC的周长.
21.(8分)如图,AD是△ABC的 BC边上的高,AE平分∠BAC,若∠B=42°,∠C=
70°,求∠AEC和∠DAE的度数.
八年级数学试题 A卷 第 5 页 (共 8 页)
22.(10分)某段河流的两岸是平行的,某数学兴趣小组在老师的带领下不用涉水过河就
能测得河的宽度,他们是这样做的:
①在河流的岸边点 B处,选对岸正对的一棵树 A;
②沿河岸直行 15m处有一棵树 C,继续前行 15m到达点 D处;
③从点 D处沿河岸垂直的方向行走,当到达 A树正好被 C树遮挡住的点 E处时,停止行
走;
④测得 DE的长为 10m.
(1)请你判断他们做法的正确性并说明理由;
(2)河的宽度是多少米?
八年级数学试题 A卷 第 6 页 (共 8 页)
23.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点 O,且 OD∥AB
交 BC于点 D,OE∥AC交 BC于点.
(1)试判定△ODE的形状,并说明你的理由;
(2)若 BC=10,求△ODE的周长.
八年级数学试题 A卷 第 7 页 (共 8 页)
24.(12分)综合与实践:数学模型可以用来解决一类问题,是数学应用基本途径.通过
探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经
验,并将其运用到更广阔的数学天地.
(1)发现问题:如图 1,在△ABC 和△AEF 中,AB=AC,AE=AF,∠BAC=∠EAF
=30°,连接 BE,CF,延长 BE交 CF于点 D.则 BE与 CF的数量关系: ,
∠BDC= °;
(2)类比探究:如图 2,在△ABC 和△AEF 中,AB=AC,AE=AF,∠BAC=∠EAF
=120°,连接 BE,CF,延长 BE,FC交于点 D.请猜想 BE与 CF的数量关系及∠BDC
的度数,并说明理由.
八年级数学试题 A卷 第 8 页 (共 8 页)
同课章节目录
