人教版2024-2025学年八年级上册数学期中试卷(含答案)
文档属性
| 名称 | 人教版2024-2025学年八年级上册数学期中试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 16:17:01 | ||
图片预览


文档简介
2024年秋季学期八年级数学期中试卷
一、选择题
1.以下面各组长度的线段为边,能组成三角形的是( )
A.,, B.,,
C.,, D.,,
2.下列图形中是轴对称图形的是( )
A. B. C. D.
3.若一个正多边形的内角和是,则该正多边形是几边形( )
A.5 B.6 C.7 D.8
4.等腰三角形的周长是,其中一边长是,则该等腰三角形的腰长为( )
A. B. C. D.或
5.如图,,点在线段上,,则的大小为( )
A. B. C. D.
6.如图,在平面直角坐标系中,点A的坐标为(2,3)且AO=BO,∠AOB=90°则点B的坐标为( )
A.(2,3) B.(-3,2) C.(-3,-2) D.(-2,3)
7.如图所示,在中,是的垂直平分线,,的周长为13cm,则的周长为( )
A.16cm B.19cm C.21cm D.25cm
8.如图,为内一点,平分,,垂足为,交于点,,,,则的长为( )
A.4 B.4.5 C.5 D.5.5
9.如图所示,,P为平分线上一点,交于点C,于点D,若,则的长为( )
A.1 B.2 C.3 D.4
10.如图,在中,,过点C作于点D,过点B作于点M,连接,过点D作,交于点N,与交于点E.下列结论:①∠;②;③;④其中正确结论有 ( )个
A.1 B.2 C.3 D.4
二、填空题
11.如果,关于轴对称,则 .
12.等腰三角形一个内角的度数是,则底角的度数是 度.
13.已知,,为的三条边,化简:= .
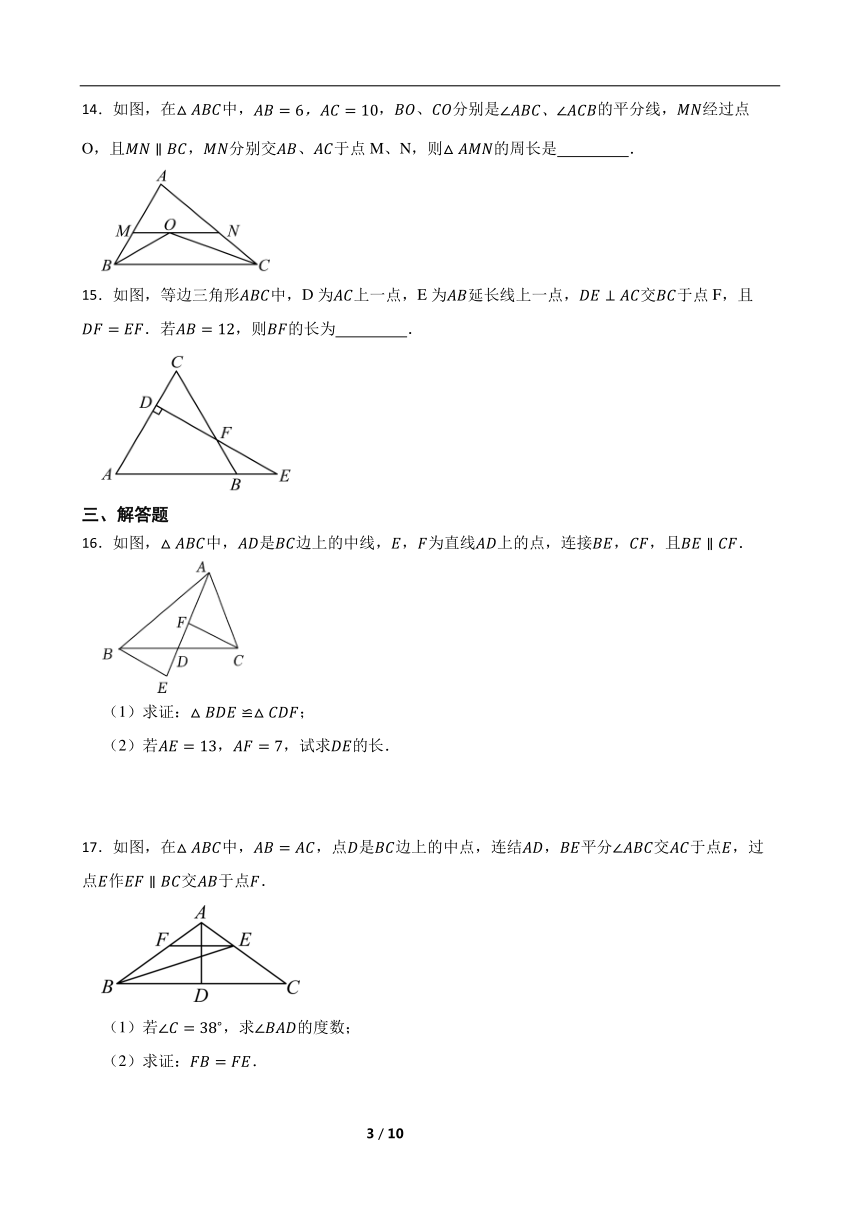
14.如图,在中,,、分别是的平分线,经过点O,且,分别交、于点M、N,则的周长是 .
15.如图,等边三角形中,D为上一点,E为延长线上一点,交于点F,且.若,则的长为 .
三、解答题
16.如图,中,是边上的中线,,为直线上的点,连接,,且.
(1)求证:;
(2)若,,试求的长.
17.如图,在中,,点是边上的中点,连结,平分交于点,过点作交于点.
(1)若,求的度数;
(2)求证:.
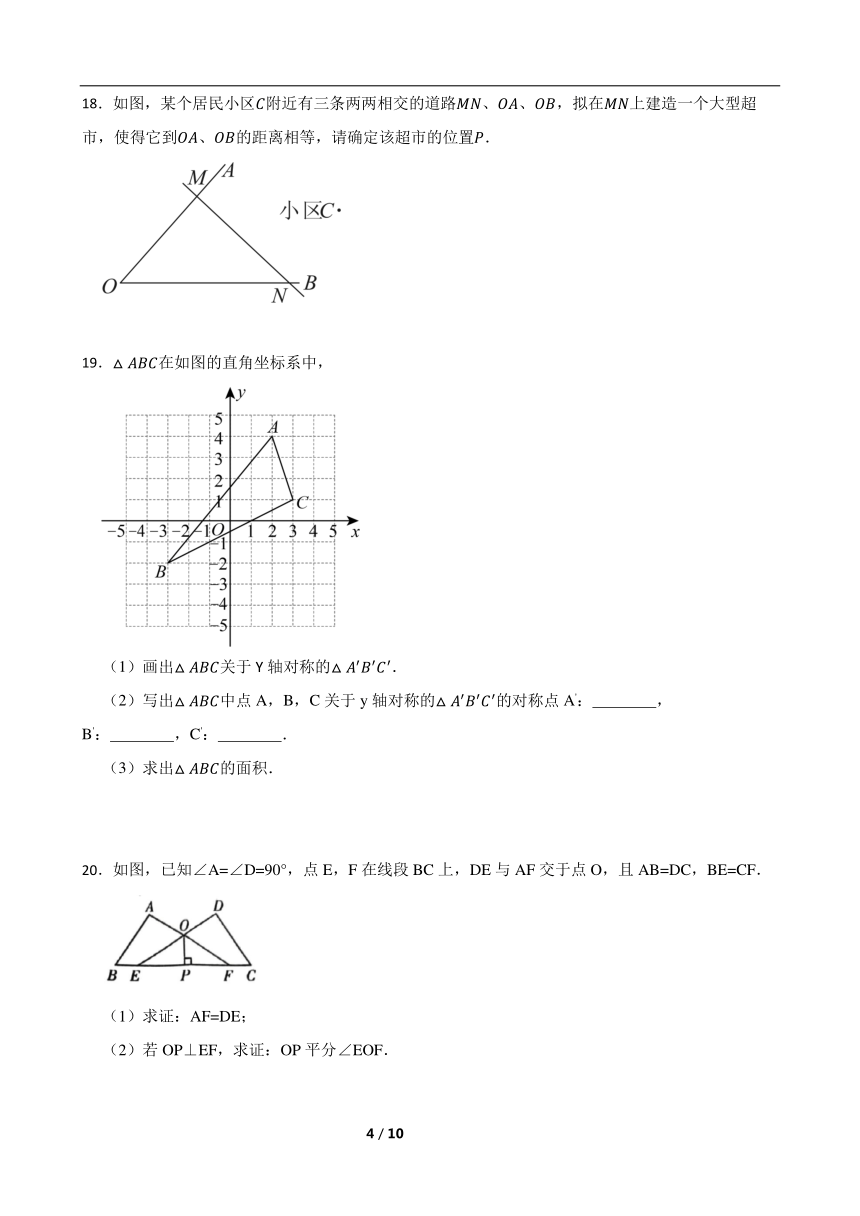
18.如图,某个居民小区附近有三条两两相交的道路、、,拟在上建造一个大型超市,使得它到、的距离相等,请确定该超市的位置.
19.在如图的直角坐标系中,
(1)画出关于Y轴对称的.
(2)写出中点A,B,C关于y轴对称的的对称点A': ,B': ,C': .
(3)求出的面积.
20.如图,已知∠A=∠D=90°,点E,F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.
(1)求证:AF=DE;
(2)若OP⊥EF,求证:OP平分∠EOF.
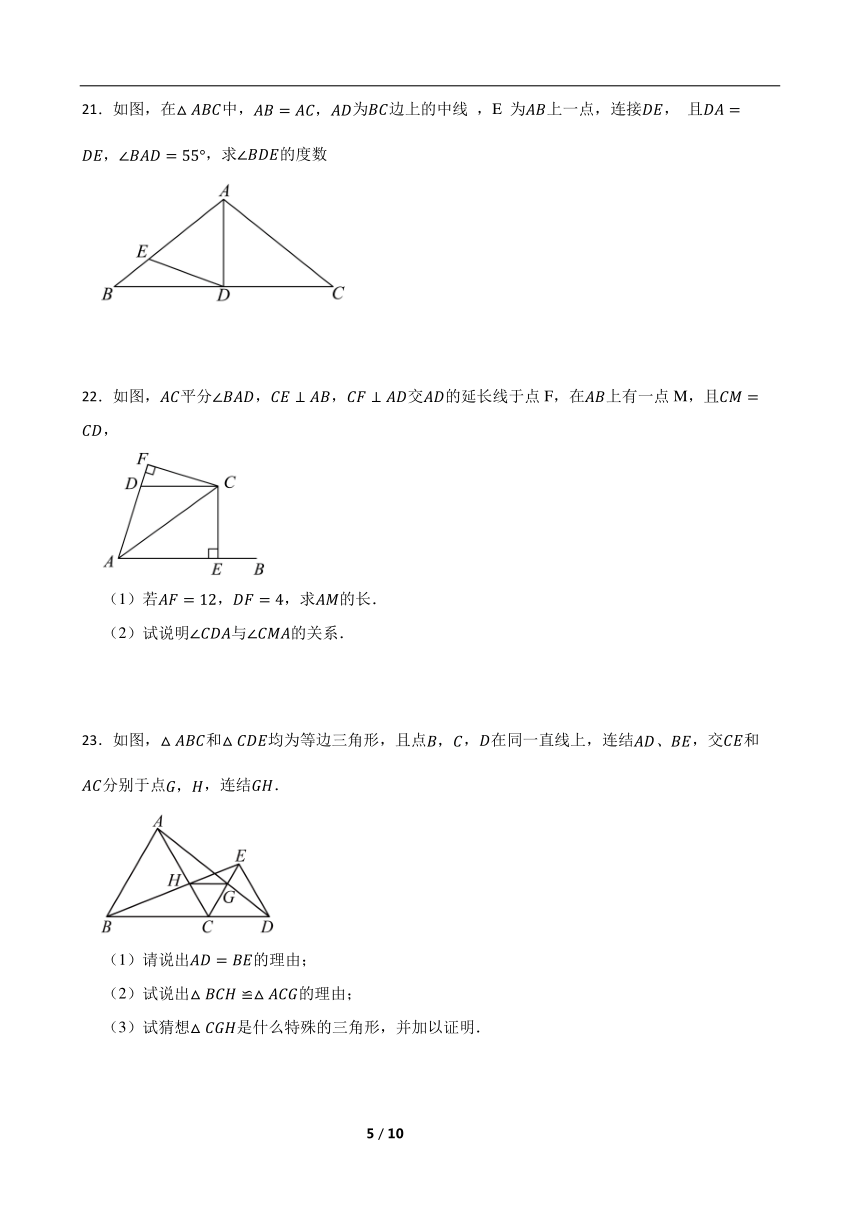
21.如图,在中,为边上的中线 ,E 为上一点,连接, 且,求的度数
22.如图,平分,,交的延长线于点F,在上有一点M,且,
(1)若,,求的长.
(2)试说明与的关系.
23.如图,和均为等边三角形,且点,在同一直线上,连结,交和分别于点,连结.
(1)请说出的理由;
(2)试说出的理由;
(3)试猜想是什么特殊的三角形,并加以证明.
24.如图,在平面直角坐标系中,为等边三角形,,点为轴上一动点,以为边作等边.
(1)求证:;
(2)的度数为 ;
(3)当点运动时,的长度是否发生变化?若不变化,直接写出的长,若变化请说出变化的规律.
(4)在轴上找一点,使是等腰三角形,直接写出满足条件的点的坐标.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】
12.【答案】或
13.【答案】
14.【答案】16
15.【答案】4
16.【答案】(1)证明:是边上的中线,
,
,
,
在和中,
,
;
(2)解:,,
,
,
,
,
.
17.【答案】(1)解:∵,
∴,
∵为的中点,,
∴,即,
∴;
(2)证明:∵平分,
∴,
∵,
∴,
∴,
∴.
18.【答案】解:如图所示:作的平分线交于点,点即为该超市的位置.
19.【答案】(1)
(2)
(3)
20.【答案】(1)证明: ∵BE= CF,
∴BE+ EF=CF+EF,即BF=CE.
∵∠A=∠D=90° ,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(HL).
∴AF=DE.
(2)由(1)知Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC
∵OP⊥EF,
∴∠OPE=∠OPF=90°.
在△OPE和△OPF中,
∴△OPE≌△OPF(AAS).
∴∠EOP=∠FOP.
∴OP平分∠EOF.
21.【答案】
22.【答案】(1)或
(2)或
23.【答案】(1)解:∵和均为等边三角形,
∴,,,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,点、、在同一条直线上,
∴,
又∵,
∴;
(3)解:是等边三角形,理由如下:
∵,
∴(全等三角形的对应边相等),
又∵,
∴是等边三角形(有一内角为度的等腰三角形为等边三角形).
24.【答案】(1)证明:∵和是等边三角形,
∴,,,
∴,
即,
在和中,
,
∴,
∴
(2)
(3)解:的长度不变,;
∵为等边三角形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴
(4)解:点M的坐标为或
1 / 1
一、选择题
1.以下面各组长度的线段为边,能组成三角形的是( )
A.,, B.,,
C.,, D.,,
2.下列图形中是轴对称图形的是( )
A. B. C. D.
3.若一个正多边形的内角和是,则该正多边形是几边形( )
A.5 B.6 C.7 D.8
4.等腰三角形的周长是,其中一边长是,则该等腰三角形的腰长为( )
A. B. C. D.或
5.如图,,点在线段上,,则的大小为( )
A. B. C. D.
6.如图,在平面直角坐标系中,点A的坐标为(2,3)且AO=BO,∠AOB=90°则点B的坐标为( )
A.(2,3) B.(-3,2) C.(-3,-2) D.(-2,3)
7.如图所示,在中,是的垂直平分线,,的周长为13cm,则的周长为( )
A.16cm B.19cm C.21cm D.25cm
8.如图,为内一点,平分,,垂足为,交于点,,,,则的长为( )
A.4 B.4.5 C.5 D.5.5
9.如图所示,,P为平分线上一点,交于点C,于点D,若,则的长为( )
A.1 B.2 C.3 D.4
10.如图,在中,,过点C作于点D,过点B作于点M,连接,过点D作,交于点N,与交于点E.下列结论:①∠;②;③;④其中正确结论有 ( )个
A.1 B.2 C.3 D.4
二、填空题
11.如果,关于轴对称,则 .
12.等腰三角形一个内角的度数是,则底角的度数是 度.
13.已知,,为的三条边,化简:= .
14.如图,在中,,、分别是的平分线,经过点O,且,分别交、于点M、N,则的周长是 .
15.如图,等边三角形中,D为上一点,E为延长线上一点,交于点F,且.若,则的长为 .
三、解答题
16.如图,中,是边上的中线,,为直线上的点,连接,,且.
(1)求证:;
(2)若,,试求的长.
17.如图,在中,,点是边上的中点,连结,平分交于点,过点作交于点.
(1)若,求的度数;
(2)求证:.
18.如图,某个居民小区附近有三条两两相交的道路、、,拟在上建造一个大型超市,使得它到、的距离相等,请确定该超市的位置.
19.在如图的直角坐标系中,
(1)画出关于Y轴对称的.
(2)写出中点A,B,C关于y轴对称的的对称点A': ,B': ,C': .
(3)求出的面积.
20.如图,已知∠A=∠D=90°,点E,F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.
(1)求证:AF=DE;
(2)若OP⊥EF,求证:OP平分∠EOF.
21.如图,在中,为边上的中线 ,E 为上一点,连接, 且,求的度数
22.如图,平分,,交的延长线于点F,在上有一点M,且,
(1)若,,求的长.
(2)试说明与的关系.
23.如图,和均为等边三角形,且点,在同一直线上,连结,交和分别于点,连结.
(1)请说出的理由;
(2)试说出的理由;
(3)试猜想是什么特殊的三角形,并加以证明.
24.如图,在平面直角坐标系中,为等边三角形,,点为轴上一动点,以为边作等边.
(1)求证:;
(2)的度数为 ;
(3)当点运动时,的长度是否发生变化?若不变化,直接写出的长,若变化请说出变化的规律.
(4)在轴上找一点,使是等腰三角形,直接写出满足条件的点的坐标.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】
12.【答案】或
13.【答案】
14.【答案】16
15.【答案】4
16.【答案】(1)证明:是边上的中线,
,
,
,
在和中,
,
;
(2)解:,,
,
,
,
,
.
17.【答案】(1)解:∵,
∴,
∵为的中点,,
∴,即,
∴;
(2)证明:∵平分,
∴,
∵,
∴,
∴,
∴.
18.【答案】解:如图所示:作的平分线交于点,点即为该超市的位置.
19.【答案】(1)
(2)
(3)
20.【答案】(1)证明: ∵BE= CF,
∴BE+ EF=CF+EF,即BF=CE.
∵∠A=∠D=90° ,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(HL).
∴AF=DE.
(2)由(1)知Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC
∵OP⊥EF,
∴∠OPE=∠OPF=90°.
在△OPE和△OPF中,
∴△OPE≌△OPF(AAS).
∴∠EOP=∠FOP.
∴OP平分∠EOF.
21.【答案】
22.【答案】(1)或
(2)或
23.【答案】(1)解:∵和均为等边三角形,
∴,,,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,点、、在同一条直线上,
∴,
又∵,
∴;
(3)解:是等边三角形,理由如下:
∵,
∴(全等三角形的对应边相等),
又∵,
∴是等边三角形(有一内角为度的等腰三角形为等边三角形).
24.【答案】(1)证明:∵和是等边三角形,
∴,,,
∴,
即,
在和中,
,
∴,
∴
(2)
(3)解:的长度不变,;
∵为等边三角形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴
(4)解:点M的坐标为或
1 / 1
同课章节目录
