北师大八上4.2一次函数与正比例函数

(共26张PPT)
第四章 一次函数
4.2一次函数与正比例函数
北师大版 数学 八年级 上册
学习目标
1.结合具体情境理解一次函数的意义，能结合实际问题中的数量关系写出一次函数的解析式。
2.能辨别正比例函数与一次函数的区别与联系。
3.能利用一次函数解决简单的实际问题。
情景导入
什么叫函数 函数的表达方式有哪些？
在某个变化过程中，有两个变量x 和y，对于变量x的每一个值，变量y都有唯一的值与它对应，那么我们称y是x的函数，其中x是自变量，y是因变量.
函数有图象、表格、关系式三种表达方式.
探索新知
一次函数与正比例函数
一
1.某弹簧的自然长度为3cm，在弹性限度内，所挂物体的质量x每增加1 kg，弹簧长度y增加0.5 cm.
（1）计算所挂物体的质量分别为1 kg，2 kg，3 kg，4 kg，5 kg时弹簧的长度，并填入下表：
（2）你能写出y与x之间的关系式吗？
x/kg 0 1 2 3 4 5 …
y/cm …
3 3.5 4 4.5 5 5.5
解：y与x之间的关系式为：y=3+0.5x.
探索新知
2.某辆汽车油箱中原有汽油60 L，汽车每行驶50 km耗油6 L.
（1）完成下表：
（2）你能写出耗油量y（L）与汽车行驶路程x（km）之间的关系式吗？
（3）你能写出油箱剩余油量z（L）与汽车行驶路程x（km）之间的关系式吗？
汽车行驶路程x/km 0 50 100 150 200 300
耗油量y/L
0
6
12
18
24
36
y=0.12x
z = 60-0.12x
探索新知
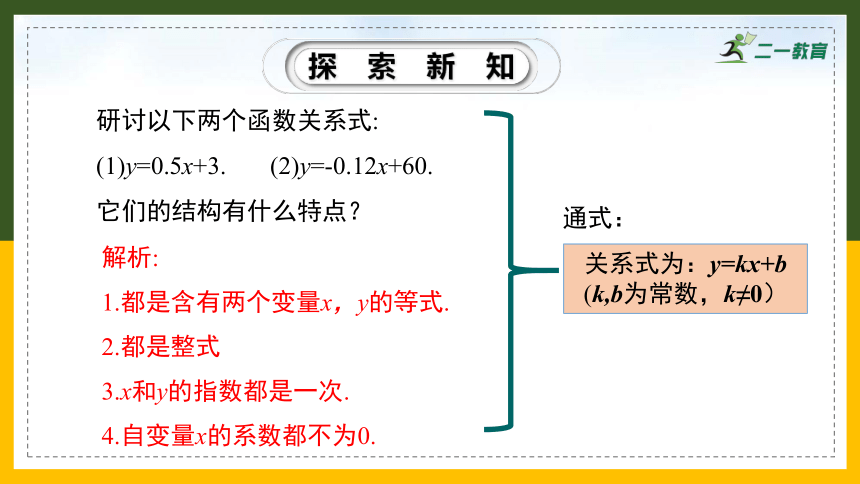
研讨以下两个函数关系式:
(1)y=0.5x+3. (2)y=-0.12x+60.
它们的结构有什么特点？
解析:
1.都是含有两个变量x，y的等式.
2.都是整式
3.x和y的指数都是一次.
4.自变量x的系数都不为0.
关系式为：y=kx+b
(k,b为常数，k≠0）
通式：
探索新知
若两个变量 x，y间的对应关系可以表示成y=kx+b (k, b为常数，k≠0）的形式，则称 y是x的一次函数.
一次函数定义：
总结归纳
次数为1
右边是一个含_______的单项式,
加上一个_____.
(2)自变量和因变量的次数都是____的。
(1)左边是________，
因变量y
自变量x
常数
一次
探索新知
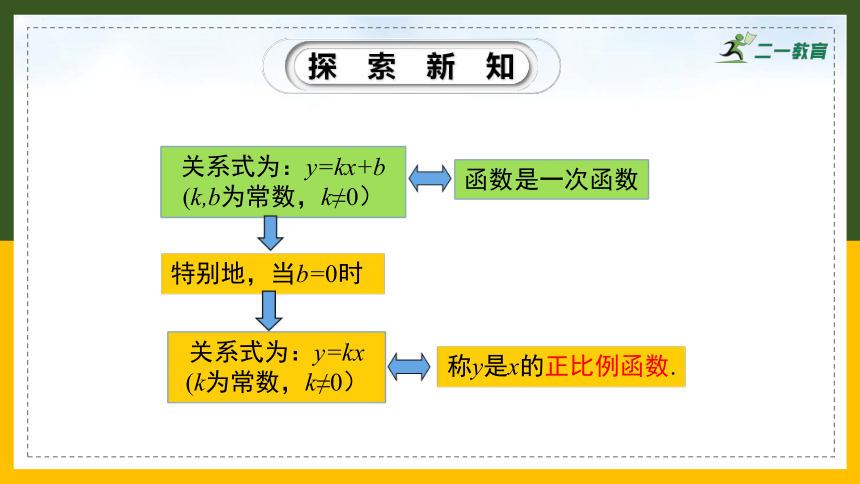
特别地，当b=0时
函数是一次函数
关系式为：y=kx+b
(k,b为常数，k≠0）
关系式为：y=kx
(k为常数，k≠0）
称y是x的正比例函数.
探索新知
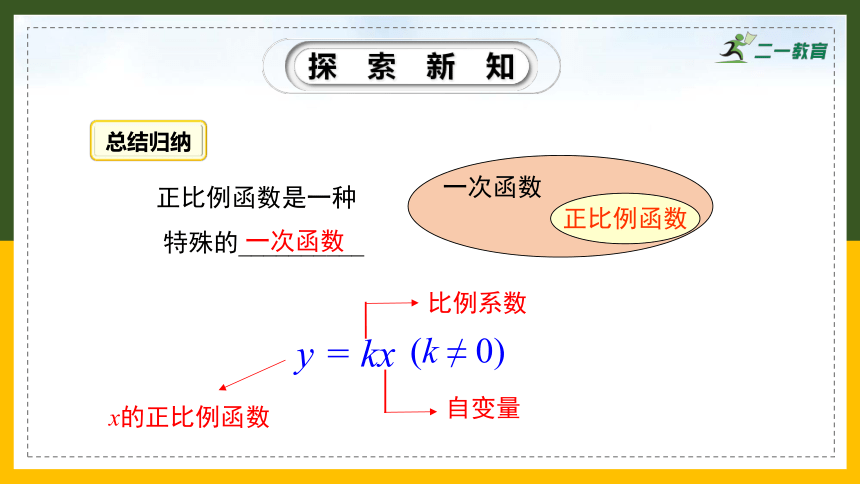
正比例函数
正比例函数是一种特殊的__________
一次函数
一次函数
y = kx
(k ≠ 0)
自变量
比例系数
x的正比例函数
总结归纳
探索新知
做一做：给出下列关系式，y是x的一次函数吗？y是x的正比例函数吗？
(1)y=﹣x－4; (2)y＝5x2－6； (3)y=2πx;
(6)y=8x2+x(1-8x);
解：一次函数有（1）（3）（4）（6）
正比例函数有（3）（4）（6）
（7）y=kx+b.
化简之后再进行判断
探索新知
1.已知函数y=(k－2)x+4－k2，当k 时，这个函数是一次函数；当k= 时，这个函数是正比例函数.
2.已知函数y=2x|m|+(m+1)，当m= 时，这个函数是一次函数；当m= 时，这个函数是正比例函数.
≠2
-2
注意：一次函数满足：
（1）k ≠ 0,自变量x的系数不为0；
（2）自变量x的指数是“1”
±1
﹣1
注意：正比例函数满足：
（1）k ≠ 0,自变量x的系数不为0；
（2）自变量x的指数是“1”
（3）b = 0
探索新知
例：写出下列各题中y与x之间的关系式，并判断：y是否为x的一次函数？是否为正比例函数？
（1）一个在斜坡上由静止开始向下滚动的小球，其速度每秒增加3m，小球的速度y(m/s)与时间x(s)之间的关系;
（2）周长为10cm的长方形的一边长为xcm，其邻边长y（cm）与x（cm）之间的关系；
（3）周长为10cm的长方形的一边长为xcm，其面积y（cm2）与x（cm）之间的关系.
探索新知
解：（1）y=3x ,y是x的一次函数,也是x的正比例函数.
（3）y=x（10÷2－x）=5x－x2 ,y不是x的一次函数,也不是x的正比例函数.
（2）y=10÷2－x=5－x ,y是x的一次函数,不是x的正比例函数.
探索新知
例：已知函数y＝(m－5)xm2－24＋m＋1.
(1)若它是一次函数，求m的值；
(2)若它是正比例函数，求m的值．
解：(1) 因为y＝(m－5)xm2－24＋m＋1是一次函数， 所以 m2－24＝1且m－5≠0，
所以 m＝±5且m≠5，所以 m＝－5.
所以，当m＝－5时，函数y＝(m－5)xm2－24＋m＋1是一次函数．
探索新知
例：已知函数y＝(m－5)xm2－24＋m＋1.
(1)若它是一次函数，求m的值；
(2)若它是正比例函数，求m的值．
解：(2)因为 y＝(m－5)xm2－24＋m＋1是一次函数，所以 m2－24＝1且m－5≠0且m＋1＝0.
所以 m＝±5且 m≠5且m＝－1，则这样的m不存在，
所以函数y＝(m－5)xm2－24＋m＋1不可能为正比例函数．
探索新知
例：我国自2019年1月1日起，我国居民个人劳务报酬所得税预扣预缴税款的计算方法是：每次收入不超过800元的，预扣预缴税款为0;每次收入超过800元但不超过4000元的，预扣预缴税款=(每次收入-800)×20%；……如某人劳务报酬2000元，他这笔所得应预扣预缴税款
(2000-800)×20% = 240(元)
探索新知
(2)某人某次取得劳务报酬3500元，他这笔所得应预扣预缴税款多少元？
(1)当每次收入大于800元但不超过4000元时，写出劳务报酬所得税预扣预缴税款y(元)与每次收入x(元)之间的关系式
解：
当每次收入大于800元但不超过4000元时
y=(x-800)×20%
即：y=0.2x-160
当x=3500时
y=0.2×3500-160
=540(元）
探索新知
(3)如果某人某次预扣预缴劳务报酬所得税600元，那么此人这次取得的劳务报酬是多少元？
因为(4000-800)×20% =640
而600<640
所以此人本次取得的劳务报酬不超过4000元
设此人本次取得的劳务报酬是x元
根据题意得：
600=0.2x-160
解得：x=3800
所以此人本次取得的劳务报酬是3800元
当堂检测
1.下列各式中，表示正比例函数的是( )
A
A. B.
C. D.
2.下列函数中， 一定是 的一次函数的是( )
B
A. B.
C. D.
当堂检测
3.下列问题中,两个变量成正比例的是( )
C
A.圆的面积 与它的半径
B.三角形面积一定时,某一边长 和该边上的高
C.正方形的周长 与它的边长
D.周长不变的长方形的长 与宽
当堂检测
4.若函数 是正比例函数，则 的值是( )
C
A.6 B.4
C.2 D.
5.函数 是关于 的一次函数，则 ， 的值
为( )
A
A. ， B. ，
C. ， D. ，
当堂检测
6.在登山过程中,海拔每升高1千米,气温下降 .已知某登山大本
营所在的位置的气温是 ,登山队员从大本营出发登山，当海拔
升高 千米时，所在位置的气温是 ,那么 关于 的函数表达
式是_ __________.

当堂检测
7.已知函数 .
（1）当 取什么值时， 是 的正比例函数？
解：因为函数 是正比例函数，
所以 且 ．解得 ．
（2）当 取什么值时， 是 的一次函数
根据一次函数的定义，可知 ，解得 ．
当堂检测
8.将长为 ，宽为 的
长方形白纸，按如图所示
（1）写出 与 的函数关系式;
解：由题意，得 .
（2）求当 时, 的值.
当 时， .
的方法黏合起来，黏合部分的宽为 .
设 张白纸黏合后的总长度为 .
一次函数与正比例函数
一次函数形式：y=kx+b（k≠0）
特别地，当b=0时，y=kx(k≠0)是正比例函数
一次函数的简单应用
感谢收看