第二十二章 22.3 实际问题与二次函数(图形、图形运动和拱桥问题) 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 第二十二章 22.3 实际问题与二次函数(图形、图形运动和拱桥问题) 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 15:00:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章 22.3 实际问题与二次函数(图形、图形运动和拱桥问题) 同步巩固练2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,用长的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为( )
A. B. C. D.
2.将一张边长为的正方形纸片的四个角分别剪去一个边长为的小正方形,然后折叠成一个无盖的长方体.当取下面哪个数值时,长方体的侧面积最大( )
A. B. C. D.
3.在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为的正方形,改建的绿地的是矩形,其中点E在上,点G在的延长线上,且.那么当为多少时,绿地的面积最大?( )
A. B. C. D.
4.如图,正方形的边长为4cm,动点P、Q同时从点A出发,以的速度分别沿和的路径向点C运动,设运动时间为x(单位:s),四边形的面积为y(单位:cm2),则y与x()之间函数关系可以用图象表示为( )
A. B.
C. D.
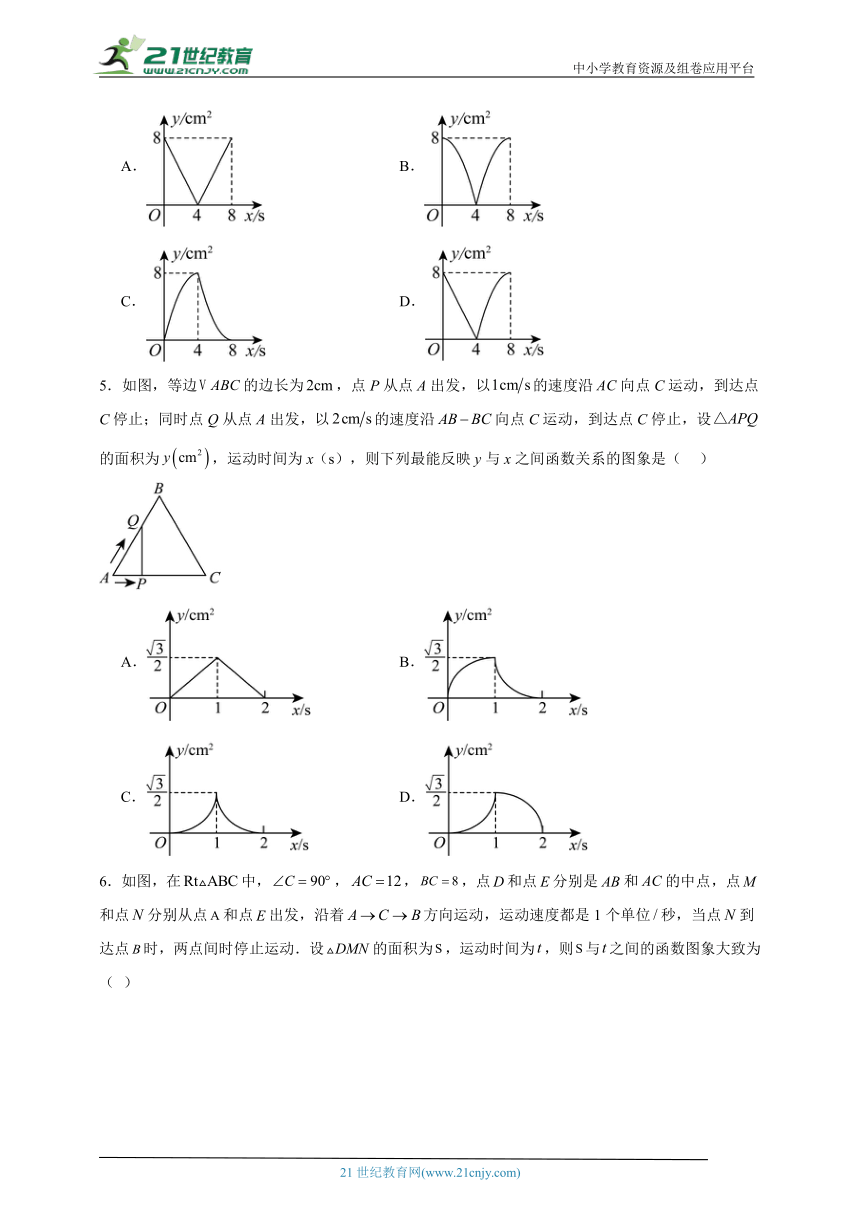
5.如图,等边的边长为,点P从点A出发,以的速度沿向点C运动,到达点C停止;同时点Q从点A出发,以的速度沿向点C运动,到达点C停止,设的面积为,运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. B.
C. D.
6.如图,在中,,,,点和点分别是和的中点,点和点分别从点和点出发,沿着方向运动,运动速度都是1个单位秒,当点到达点时,两点间时停止运动.设的面积为,运动时间为,则与之间的函数图象大致为( )
A. B.
C. D.
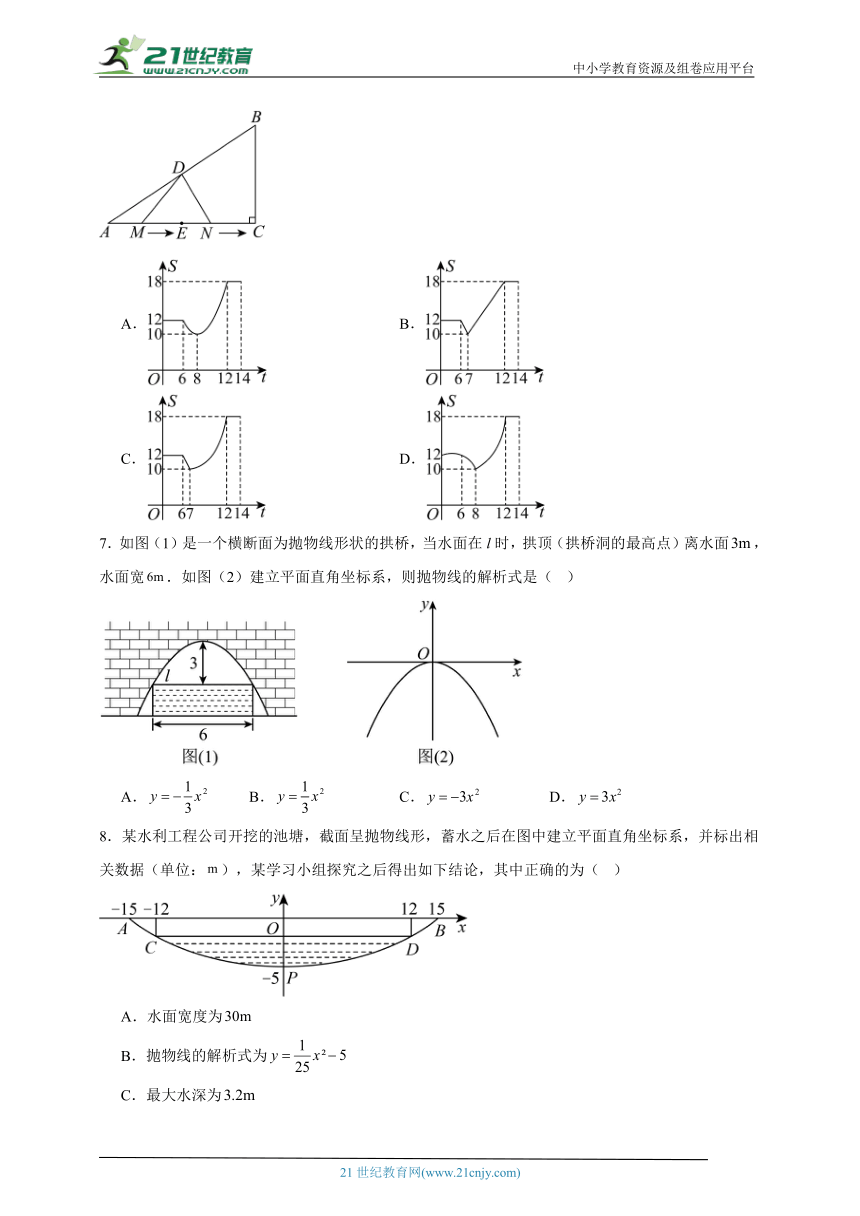
7.如图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面,水面宽.如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
8.某水利工程公司开挖的池塘,截面呈抛物线形,蓄水之后在图中建立平面直角坐标系,并标出相关数据(单位:),某学习小组探究之后得出如下结论,其中正确的为( )
A.水面宽度为
B.抛物线的解析式为
C.最大水深为
D.若池塘中水面的宽度减少为原来的一半,则最大水深减少为原来的
9.如图,福州西湖公园上有一座造型为抛物线形状的拱桥,因其宛如玉带,从而被人称为玉带桥,经测量,玉带桥的拱顶离水面的平均高度为,若玉带桥所在的这条抛物线表示的二次函数为,则该抛物线所在的平面直角坐标系是如下的( )
A.以抛物线的顶点为原点,以抛物线的对称轴为轴
B.以抛物线与水面的左交点为原点,以水面为轴
C.以水面为轴,以抛物线的对称轴为轴
D.以图中夕阳所在位置为原点,以抛物线的对称轴为轴
10.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图2所示建立坐标系,在正常水位时水面宽米,当水位上升5米时,则水面宽米,则函数表达式为( )
A. B. C. D.
二、填空题
11.某广告公司设计一块周长为米的矩形广告牌,设矩形的一边长为米,广告牌的面积为平方米,则广告牌的面积与的函数关系式为 ,自变量的取值范围是 .
12.如图,相框长,宽,相框边的宽为,相框内的面积是,则相框内的长和宽分别为 、 ,y与x之间的函数关系式为 .
13.如图,在中,,,,点P从点A沿向点C以的速度运动,同时点Q从点C沿向点B以的速度运到(点Q运动到点B停止),在运动过程中,四边形的面积最小值为 .
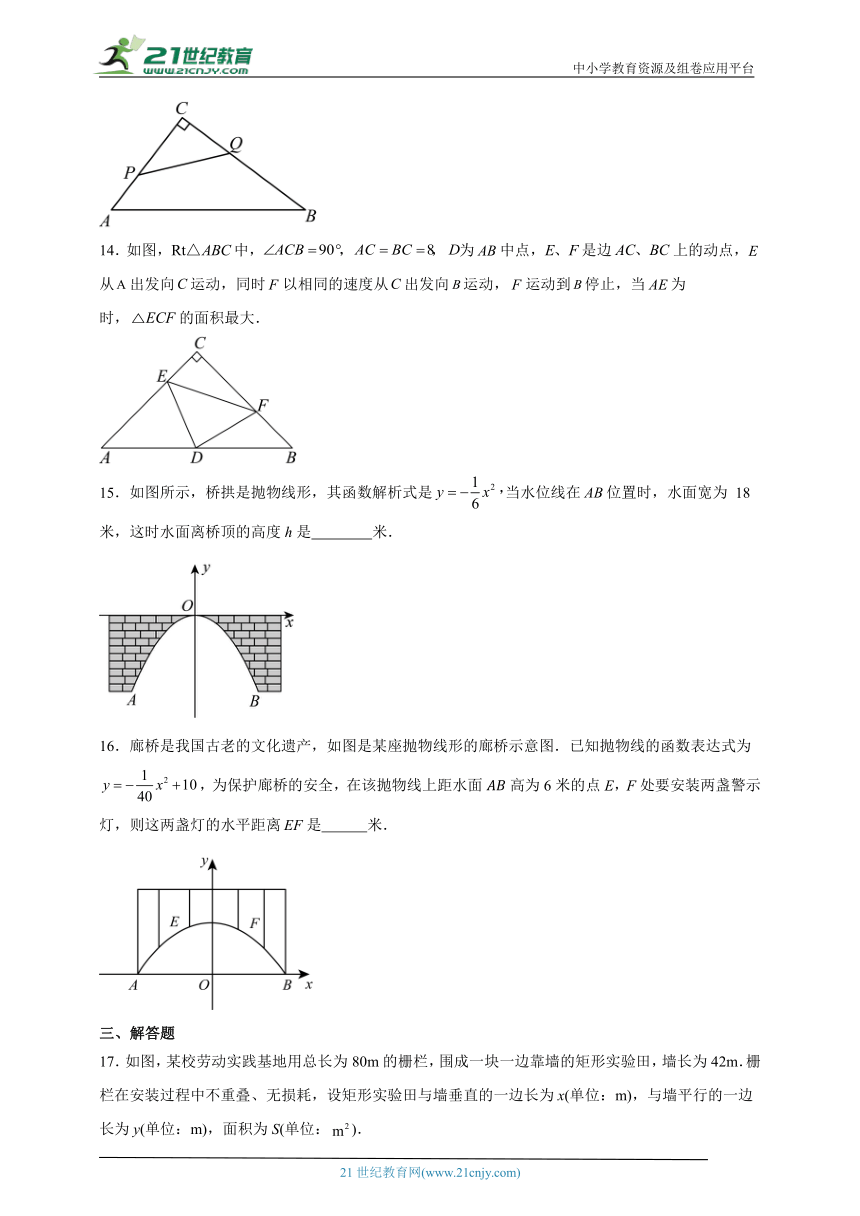
14.如图,中,为中点,是边上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止,当为 时,的面积最大.
15.如图所示,桥拱是抛物线形,其函数解析式是当水位线在位置时,水面宽为 18米,这时水面离桥顶的高度h是 米.
16.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为6米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是 米.
三、解答题
17.如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
18.与是两个直角边都等于4厘米的等腰直角三角形,、分别是直角边、的中点.位置固定,按如图叠放,使斜边在直线上,顶点与点M重合.等腰直角以1厘米/秒的速度沿直线向右平移,直到点与点N重合.设x秒时,与重叠部分面积为y平方厘米.
(1)求y与x的函数关系式;
(2)当与重叠部分面积为平方厘米时,求移动的时间.
19.如图,要修建一条截面为抛物线型的隧道,线段表示水平的路面,根据设计要求:,该抛物线的顶点到的距离为.
(1)请建立合适的平面直角坐标系,并求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上同一高度处安装照明灯(即在该抛物线上的点,处分别安装照明灯).若要求,处的照明灯水平距离为,求照明灯的高度.
参考答案:
1.C
解:设半圆的直径为x,矩形的高度为y,窗户透光面积为S,
则窗框总长,
∴,
∴,
∵,
∴S有最大值,为.
2.B
解:依题意设侧面积为;
∴,
∵,
∴有最大值,当时,面积最大,
3.B
解:设,则,绿地的面积为,
根据题意得:
,
∵二次项系数为,
∴当时,y有最大值72.
即当时,绿地面积最大.
4.B
解:①时,
∵正方形的边长为4cm,
∴;
②时,
∵正方形的边长为4cm,
∴;
所以,y与x之间的函数关系可以用两段二次函数图象表示,只有B选项图象符合.
5.D
由题意得,点Q移动的路程为,点P移动的路程为x,
∵为等边三角形,
∴,
①当点Q在线段上时,过点Q作于点D,
∴,
∵,
∴,
∴,即,
∴当时,函数图象为开口向上的抛物线的一部分,故选项A、B排除;
②当点Q在线段上时,过点Q作于点E,
∴,
∵,
∴,
∴,即,
∴当时,函数图象为开口向下的抛物线的一部分,故选项C排除;
6.A
解:如图,取的中点F,连接,
,
点、是中点,
∴,,
∵,
∴四边形为矩形,
当时,点在上,点在上,,
;
如图,当时,点在上,点在上,
,
,,,
;
如图,当时,点、都在上,
,
综上判断选项A的图象符合题意.
7.A
解:设出抛物线方程,
由图象可知该图象经过点,
故,
,
故,
8.C
解:设解析式为,
将抛物线上点,
带入抛物线解析式中得,
解得,
解析式为.
选项A中,,,水面宽度为故选项A错误,不符合题意;
选项B中,解析式为,故选项B错误,不符合题意;
选项C中,池塘水深最深处为点,水面,所以水深最深处为点到水面的距离为米,故选项C正确,符合题意;
选项D中,若池塘中水面的宽度减少为原来的一半,由抛物线关于轴对称可知,抛物线上点横坐标,带入解析式算得,即到水面距离为米,而最深处到水面的距离为米,减少为原来的.故选项D错误,不符合题意.
9.C
解:由抛物线的图象与性质可知,二次函数为的对称轴为轴,顶点坐标为,
该抛物线所在的平面直角坐标系是以水面为轴,以抛物线的对称轴为轴,
10.B
解:设函数表达式为,
∵
设点
∵当水位上升5米时,则水面宽米
∴
把,分别代入
得出
解得
∴函数表达式为,
11.
解:∵周长为米的矩形广告牌,设矩形的一边长为米,
∴另一边长为米,.
∵,
解得:;
故答案是:,
12.
解:相框长,宽,相框边的宽为,
相框内的长为,相框内的宽为,
根据题意,得
展开得:
整理得:
根据题意,得
解得:.
∴y与x之间的函数关系式为,
故答案为:,,.
13.
解:在中,,,,
,
设运动时间为,则,,
当时,四边形的面积取最小值,最小值为.
故答案为:15.
14.4
解:根据题意,设点运动的距离,则点运动的距离,
,
,
,
,
,
抛物线开口向下,当时,的面积最大,即当时,的面积最大,
故答案为:4.
15.
解:∵,
∴由题意知,当时,,
所以,水面离桥顶的高度h是米,
故答案为:
16.
解:当时,则,
解得
∴(米)
故答案为
17.(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
18.(1)
(2)或秒
(1)解:∵等腰直角三角形的直角边都为4,即
∴,,
∵且分别是直角边、的中点.
∴,,
当在上时,为等腰直角三角形,则
此时,;
当在上时,,
当在上时,,
①如图1,当时,,过点作,则为等腰直角三角形,则,且,
∴,
由平移可知,则重叠部分为平行四边形,
则;
②如图2,当时,如图、、 、是等腰直角三角形,
∵,则,,
∴,,
∴,,
则
即;
③如图3,当时,
,,,
类比①可知,;
综上所述,;
(2)∵
∴当时,重叠部分面积随增大而增大;
当时,重叠部分面积随增大而减小;
当时,;当时,;
综上所述,当与重叠部分面积为平方厘米时, 移动的时间为或秒.
19.(1)
(2)
(1)解:以为坐标原点,以所在直线为轴,以过点垂直于轴的直线为轴,建立平面直角坐标系.
由题意,得点,顶点,
设抛物线的函数表达式为,
把代入,得,
解得,
满足设计要求的抛物线的函数表达式为.
(2)解:点,在同一高度,
点,关于对称轴直线对称,
∵,处的照明灯水平距离为,
∴可知点距离对称轴个单位长度,
点的横坐标为,
在中,当时,
点的纵坐标为,
即照明灯的高度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十二章 22.3 实际问题与二次函数(图形、图形运动和拱桥问题) 同步巩固练2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,用长的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为( )
A. B. C. D.
2.将一张边长为的正方形纸片的四个角分别剪去一个边长为的小正方形,然后折叠成一个无盖的长方体.当取下面哪个数值时,长方体的侧面积最大( )
A. B. C. D.
3.在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为的正方形,改建的绿地的是矩形,其中点E在上,点G在的延长线上,且.那么当为多少时,绿地的面积最大?( )
A. B. C. D.
4.如图,正方形的边长为4cm,动点P、Q同时从点A出发,以的速度分别沿和的路径向点C运动,设运动时间为x(单位:s),四边形的面积为y(单位:cm2),则y与x()之间函数关系可以用图象表示为( )
A. B.
C. D.
5.如图,等边的边长为,点P从点A出发,以的速度沿向点C运动,到达点C停止;同时点Q从点A出发,以的速度沿向点C运动,到达点C停止,设的面积为,运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. B.
C. D.
6.如图,在中,,,,点和点分别是和的中点,点和点分别从点和点出发,沿着方向运动,运动速度都是1个单位秒,当点到达点时,两点间时停止运动.设的面积为,运动时间为,则与之间的函数图象大致为( )
A. B.
C. D.
7.如图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面,水面宽.如图(2)建立平面直角坐标系,则抛物线的解析式是( )
A. B. C. D.
8.某水利工程公司开挖的池塘,截面呈抛物线形,蓄水之后在图中建立平面直角坐标系,并标出相关数据(单位:),某学习小组探究之后得出如下结论,其中正确的为( )
A.水面宽度为
B.抛物线的解析式为
C.最大水深为
D.若池塘中水面的宽度减少为原来的一半,则最大水深减少为原来的
9.如图,福州西湖公园上有一座造型为抛物线形状的拱桥,因其宛如玉带,从而被人称为玉带桥,经测量,玉带桥的拱顶离水面的平均高度为,若玉带桥所在的这条抛物线表示的二次函数为,则该抛物线所在的平面直角坐标系是如下的( )
A.以抛物线的顶点为原点,以抛物线的对称轴为轴
B.以抛物线与水面的左交点为原点,以水面为轴
C.以水面为轴,以抛物线的对称轴为轴
D.以图中夕阳所在位置为原点,以抛物线的对称轴为轴
10.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图2所示建立坐标系,在正常水位时水面宽米,当水位上升5米时,则水面宽米,则函数表达式为( )
A. B. C. D.
二、填空题
11.某广告公司设计一块周长为米的矩形广告牌,设矩形的一边长为米,广告牌的面积为平方米,则广告牌的面积与的函数关系式为 ,自变量的取值范围是 .
12.如图,相框长,宽,相框边的宽为,相框内的面积是,则相框内的长和宽分别为 、 ,y与x之间的函数关系式为 .
13.如图,在中,,,,点P从点A沿向点C以的速度运动,同时点Q从点C沿向点B以的速度运到(点Q运动到点B停止),在运动过程中,四边形的面积最小值为 .
14.如图,中,为中点,是边上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止,当为 时,的面积最大.
15.如图所示,桥拱是抛物线形,其函数解析式是当水位线在位置时,水面宽为 18米,这时水面离桥顶的高度h是 米.
16.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为6米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是 米.
三、解答题
17.如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
18.与是两个直角边都等于4厘米的等腰直角三角形,、分别是直角边、的中点.位置固定,按如图叠放,使斜边在直线上,顶点与点M重合.等腰直角以1厘米/秒的速度沿直线向右平移,直到点与点N重合.设x秒时,与重叠部分面积为y平方厘米.
(1)求y与x的函数关系式;
(2)当与重叠部分面积为平方厘米时,求移动的时间.
19.如图,要修建一条截面为抛物线型的隧道,线段表示水平的路面,根据设计要求:,该抛物线的顶点到的距离为.
(1)请建立合适的平面直角坐标系,并求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上同一高度处安装照明灯(即在该抛物线上的点,处分别安装照明灯).若要求,处的照明灯水平距离为,求照明灯的高度.
参考答案:
1.C
解:设半圆的直径为x,矩形的高度为y,窗户透光面积为S,
则窗框总长,
∴,
∴,
∵,
∴S有最大值,为.
2.B
解:依题意设侧面积为;
∴,
∵,
∴有最大值,当时,面积最大,
3.B
解:设,则,绿地的面积为,
根据题意得:
,
∵二次项系数为,
∴当时,y有最大值72.
即当时,绿地面积最大.
4.B
解:①时,
∵正方形的边长为4cm,
∴;
②时,
∵正方形的边长为4cm,
∴;
所以,y与x之间的函数关系可以用两段二次函数图象表示,只有B选项图象符合.
5.D
由题意得,点Q移动的路程为,点P移动的路程为x,
∵为等边三角形,
∴,
①当点Q在线段上时,过点Q作于点D,
∴,
∵,
∴,
∴,即,
∴当时,函数图象为开口向上的抛物线的一部分,故选项A、B排除;
②当点Q在线段上时,过点Q作于点E,
∴,
∵,
∴,
∴,即,
∴当时,函数图象为开口向下的抛物线的一部分,故选项C排除;
6.A
解:如图,取的中点F,连接,
,
点、是中点,
∴,,
∵,
∴四边形为矩形,
当时,点在上,点在上,,
;
如图,当时,点在上,点在上,
,
,,,
;
如图,当时,点、都在上,
,
综上判断选项A的图象符合题意.
7.A
解:设出抛物线方程,
由图象可知该图象经过点,
故,
,
故,
8.C
解:设解析式为,
将抛物线上点,
带入抛物线解析式中得,
解得,
解析式为.
选项A中,,,水面宽度为故选项A错误,不符合题意;
选项B中,解析式为,故选项B错误,不符合题意;
选项C中,池塘水深最深处为点,水面,所以水深最深处为点到水面的距离为米,故选项C正确,符合题意;
选项D中,若池塘中水面的宽度减少为原来的一半,由抛物线关于轴对称可知,抛物线上点横坐标,带入解析式算得,即到水面距离为米,而最深处到水面的距离为米,减少为原来的.故选项D错误,不符合题意.
9.C
解:由抛物线的图象与性质可知,二次函数为的对称轴为轴,顶点坐标为,
该抛物线所在的平面直角坐标系是以水面为轴,以抛物线的对称轴为轴,
10.B
解:设函数表达式为,
∵
设点
∵当水位上升5米时,则水面宽米
∴
把,分别代入
得出
解得
∴函数表达式为,
11.
解:∵周长为米的矩形广告牌,设矩形的一边长为米,
∴另一边长为米,.
∵,
解得:;
故答案是:,
12.
解:相框长,宽,相框边的宽为,
相框内的长为,相框内的宽为,
根据题意,得
展开得:
整理得:
根据题意,得
解得:.
∴y与x之间的函数关系式为,
故答案为:,,.
13.
解:在中,,,,
,
设运动时间为,则,,
当时,四边形的面积取最小值,最小值为.
故答案为:15.
14.4
解:根据题意,设点运动的距离,则点运动的距离,
,
,
,
,
,
抛物线开口向下,当时,的面积最大,即当时,的面积最大,
故答案为:4.
15.
解:∵,
∴由题意知,当时,,
所以,水面离桥顶的高度h是米,
故答案为:
16.
解:当时,则,
解得
∴(米)
故答案为
17.(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
18.(1)
(2)或秒
(1)解:∵等腰直角三角形的直角边都为4,即
∴,,
∵且分别是直角边、的中点.
∴,,
当在上时,为等腰直角三角形,则
此时,;
当在上时,,
当在上时,,
①如图1,当时,,过点作,则为等腰直角三角形,则,且,
∴,
由平移可知,则重叠部分为平行四边形,
则;
②如图2,当时,如图、、 、是等腰直角三角形,
∵,则,,
∴,,
∴,,
则
即;
③如图3,当时,
,,,
类比①可知,;
综上所述,;
(2)∵
∴当时,重叠部分面积随增大而增大;
当时,重叠部分面积随增大而减小;
当时,;当时,;
综上所述,当与重叠部分面积为平方厘米时, 移动的时间为或秒.
19.(1)
(2)
(1)解:以为坐标原点,以所在直线为轴,以过点垂直于轴的直线为轴,建立平面直角坐标系.
由题意,得点,顶点,
设抛物线的函数表达式为,
把代入,得,
解得,
满足设计要求的抛物线的函数表达式为.
(2)解:点,在同一高度,
点,关于对称轴直线对称,
∵,处的照明灯水平距离为,
∴可知点距离对称轴个单位长度,
点的横坐标为,
在中,当时,
点的纵坐标为,
即照明灯的高度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
