第二十一章 21.2.4 实际问题与一元二次方程 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 第二十一章 21.2.4 实际问题与一元二次方程 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十一章 21.2.4 实际问题与一元二次方程 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.若某QQ群所有成员都向群内其他人发一条信息,共发出4950条信息,设这个群有x人,则可列方程为( )
A. B.
C. D.
2.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共91.若设主干长出x个支干,则可列方程正确的是( )
A.(1+x)2=91 B.1+x+x2=91 C.1+x2=91 D.x+x2=91
3.某市商品房的均价原为18150元,经过连续两次降价后均价为15000元.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A. B.
C. D.
4.从盛满升纯药液的容器中,倒出升药液后,用水加满;混合后,第二次又倒出升的混合药液,再用水加满,此时容器内的药液浓度为,则根据题意所得的方程正确的是( )
A. B.
C. D.
5.如图,要为一幅长为29cm,宽为22cm的照片配一个相框,要求相框的四条边宽度相等,且相框所占面积为照片面积的四分之一,相框边的宽度为xcm,则可列方程为( )
A.(29﹣2x)(22﹣2x)=×29×22
B.(29﹣2x)(22﹣2x)=×29×22
C.(29﹣x)(22﹣x)=×29×22
D.(29﹣x)(22﹣x)=×29×22
6.为增强学生体质,某学校准备开展足球比赛,赛制为单循环形式,现计划安排场比赛,则共有几支队伍参赛( )
A. B. C. D.
7.若两个连续偶数的积是288.则这两个偶数的和等于( )
A.43或—43 B.43 C.34或—34 D.—34
8.如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若,则的长为( )
A.9 B.12 C.15 D.16
二、填空题
9.有2个人患了流感,经过两轮传染后共有144人患了流感,若每轮传染中平均一个人传染了x人,则可列方程为 .
10.某药品经过连续两次降价后,由每盒200元下调至128元,若平均每次下降百分率为x,则所列方程为
11.如图,在中,,,,动点从点出发,沿方向运动,动点从点出发,沿方向运动,如果点,同时出发,,的运动速度均为.那么运动 秒时,它们相距.
12.某印刷厂3月份印刷了50万册书籍,5月份印刷了72万册书籍,如果每月印刷的增长率都为x,则根据题意,可建立关于x的方程是 .
13.某种童鞋原价为100元,由于店面转让要清仓,现连续两次降价处理,共降价64元后出售,已知两次降价的百分率相同,则每次降价的百分率为 .
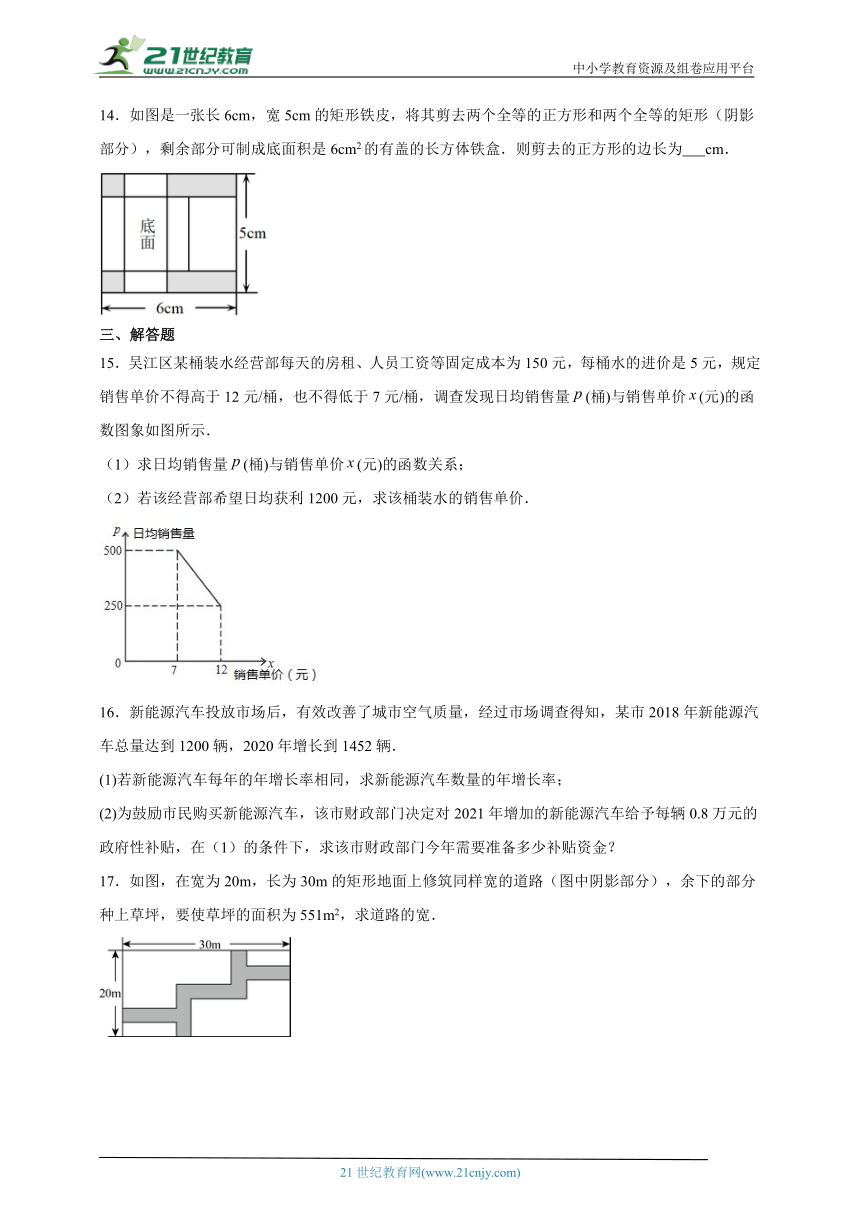
14.如图是一张长6cm,宽5cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形(阴影部分),剩余部分可制成底面积是6cm2的有盖的长方体铁盒.则剪去的正方形的边长为 cm.
三、解答题
15.吴江区某桶装水经营部每天的房租、人员工资等固定成本为150元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量(桶)与销售单价(元)的函数图象如图所示.
(1)求日均销售量(桶)与销售单价(元)的函数关系;
(2)若该经营部希望日均获利1200元,求该桶装水的销售单价.
16.新能源汽车投放市场后,有效改善了城市空气质量,经过市场调查得知,某市2018年新能源汽车总量达到1200辆,2020年增长到1452辆.
(1)若新能源汽车每年的年增长率相同,求新能源汽车数量的年增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对2021年增加的新能源汽车给予每辆0.8万元的政府性补贴,在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
17.如图,在宽为20m,长为30m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为551m2,求道路的宽.
参考答案:
1.B
解:设这个群有x人,则可列方程为.
2.B
设主干长出x个支干,根据题意,得
1+x+x2=91
3.D
设平均每次降价的百分率为x,
根据题意得,.
4.B
解:设每次倒出液体x升,则第一次倒出后容器内剩下纯药液升,
加满水后药液的浓度为,
依题意得: 即.
5.B
设相框边的宽度为xcm,则可列方程为:
(29﹣2x)(22﹣2x)=×29×22.
6.B
解:设共有支队伍参赛,进行单循环赛制,
∴,整理得,,
∴(舍去),,
7.C
解:设一个偶数为x,则另一个偶数为x+2,
则有x(x+2)=288,
解得x1=16,x2=-18.
∴二者之和为16+18=34或-18-16=-34.
8.A
解:设,则,
四边形是矩形,
∴,
∵将沿翻折,点A恰好落在边上的点F处,
∴,
∵
∴,
∵在中,,
∴
解得:(舍去)
∴,
∴,
9.2+2x+x(2x+2)=144
解:设每轮传染中平均一个人传染了x人,
依题意得方程为:2+2x+x(2x+2)=144,
故答案为:2+2x+x(2x+2)=144.
10.200(1-x)2=128
解:设平均每次下降百分率为x,
根据题意可得
200(1-x)2=128
故答案为:200(1-x)2=128.
11.9或12
解:设运动秒时,,两点相距15厘米,
依题意,得:,
解得:,,
运动9秒或12秒时,,两点相距15厘米;
故答案为:9或12.
12.50(1+x)2=72.
解:设每月印刷的增长率都为x,
根据题意得:50(1+x)2=72.
故答案为50(1+x)2=72.
13.
解:设每次降价的百分率为,依题意得,
,
解得:(舍去),
故答案为:.
14.1.
设底面长为acm,宽为bcm,正方形边长为xcm,
由题意得:,
由②得a=5-2x,由 ①得b=3-x,代入③中得: (5-2x)(3-x)=6
整理得:2x2-11x+9=0.
因式分解得(x-1)(2x-9)=0
解得x=1或x=4.5(舍去).
故答案为1.
15.(1);(2)8元.
解:(1)设,
将代入得
,
∴日均销售量(桶)与销售单价(元)的函数关系式为:
(2)由题意,得:
答:该经营部希望日均获利1200元,求该桶装水的销售单价为8元.
16.(1)
(2)116.16万元
(1)解:设今、明两年新能源汽车数量的平均增长率为,
由题意,得,
解得,,(舍去),
答:今、明两年新能源汽车数量的平均增长率为;
(2)解:(万元),
答:该市财政部门今年需要准备116.16万元补贴资金.
17.
解:设道路的宽为,根据题意得:
,
解得:,(不合题意,舍去),
答:道路的宽为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章 21.2.4 实际问题与一元二次方程 同步巩固练 2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.若某QQ群所有成员都向群内其他人发一条信息,共发出4950条信息,设这个群有x人,则可列方程为( )
A. B.
C. D.
2.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共91.若设主干长出x个支干,则可列方程正确的是( )
A.(1+x)2=91 B.1+x+x2=91 C.1+x2=91 D.x+x2=91
3.某市商品房的均价原为18150元,经过连续两次降价后均价为15000元.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A. B.
C. D.
4.从盛满升纯药液的容器中,倒出升药液后,用水加满;混合后,第二次又倒出升的混合药液,再用水加满,此时容器内的药液浓度为,则根据题意所得的方程正确的是( )
A. B.
C. D.
5.如图,要为一幅长为29cm,宽为22cm的照片配一个相框,要求相框的四条边宽度相等,且相框所占面积为照片面积的四分之一,相框边的宽度为xcm,则可列方程为( )
A.(29﹣2x)(22﹣2x)=×29×22
B.(29﹣2x)(22﹣2x)=×29×22
C.(29﹣x)(22﹣x)=×29×22
D.(29﹣x)(22﹣x)=×29×22
6.为增强学生体质,某学校准备开展足球比赛,赛制为单循环形式,现计划安排场比赛,则共有几支队伍参赛( )
A. B. C. D.
7.若两个连续偶数的积是288.则这两个偶数的和等于( )
A.43或—43 B.43 C.34或—34 D.—34
8.如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若,则的长为( )
A.9 B.12 C.15 D.16
二、填空题
9.有2个人患了流感,经过两轮传染后共有144人患了流感,若每轮传染中平均一个人传染了x人,则可列方程为 .
10.某药品经过连续两次降价后,由每盒200元下调至128元,若平均每次下降百分率为x,则所列方程为
11.如图,在中,,,,动点从点出发,沿方向运动,动点从点出发,沿方向运动,如果点,同时出发,,的运动速度均为.那么运动 秒时,它们相距.
12.某印刷厂3月份印刷了50万册书籍,5月份印刷了72万册书籍,如果每月印刷的增长率都为x,则根据题意,可建立关于x的方程是 .
13.某种童鞋原价为100元,由于店面转让要清仓,现连续两次降价处理,共降价64元后出售,已知两次降价的百分率相同,则每次降价的百分率为 .
14.如图是一张长6cm,宽5cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形(阴影部分),剩余部分可制成底面积是6cm2的有盖的长方体铁盒.则剪去的正方形的边长为 cm.
三、解答题
15.吴江区某桶装水经营部每天的房租、人员工资等固定成本为150元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量(桶)与销售单价(元)的函数图象如图所示.
(1)求日均销售量(桶)与销售单价(元)的函数关系;
(2)若该经营部希望日均获利1200元,求该桶装水的销售单价.
16.新能源汽车投放市场后,有效改善了城市空气质量,经过市场调查得知,某市2018年新能源汽车总量达到1200辆,2020年增长到1452辆.
(1)若新能源汽车每年的年增长率相同,求新能源汽车数量的年增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对2021年增加的新能源汽车给予每辆0.8万元的政府性补贴,在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
17.如图,在宽为20m,长为30m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为551m2,求道路的宽.
参考答案:
1.B
解:设这个群有x人,则可列方程为.
2.B
设主干长出x个支干,根据题意,得
1+x+x2=91
3.D
设平均每次降价的百分率为x,
根据题意得,.
4.B
解:设每次倒出液体x升,则第一次倒出后容器内剩下纯药液升,
加满水后药液的浓度为,
依题意得: 即.
5.B
设相框边的宽度为xcm,则可列方程为:
(29﹣2x)(22﹣2x)=×29×22.
6.B
解:设共有支队伍参赛,进行单循环赛制,
∴,整理得,,
∴(舍去),,
7.C
解:设一个偶数为x,则另一个偶数为x+2,
则有x(x+2)=288,
解得x1=16,x2=-18.
∴二者之和为16+18=34或-18-16=-34.
8.A
解:设,则,
四边形是矩形,
∴,
∵将沿翻折,点A恰好落在边上的点F处,
∴,
∵
∴,
∵在中,,
∴
解得:(舍去)
∴,
∴,
9.2+2x+x(2x+2)=144
解:设每轮传染中平均一个人传染了x人,
依题意得方程为:2+2x+x(2x+2)=144,
故答案为:2+2x+x(2x+2)=144.
10.200(1-x)2=128
解:设平均每次下降百分率为x,
根据题意可得
200(1-x)2=128
故答案为:200(1-x)2=128.
11.9或12
解:设运动秒时,,两点相距15厘米,
依题意,得:,
解得:,,
运动9秒或12秒时,,两点相距15厘米;
故答案为:9或12.
12.50(1+x)2=72.
解:设每月印刷的增长率都为x,
根据题意得:50(1+x)2=72.
故答案为50(1+x)2=72.
13.
解:设每次降价的百分率为,依题意得,
,
解得:(舍去),
故答案为:.
14.1.
设底面长为acm,宽为bcm,正方形边长为xcm,
由题意得:,
由②得a=5-2x,由 ①得b=3-x,代入③中得: (5-2x)(3-x)=6
整理得:2x2-11x+9=0.
因式分解得(x-1)(2x-9)=0
解得x=1或x=4.5(舍去).
故答案为1.
15.(1);(2)8元.
解:(1)设,
将代入得
,
∴日均销售量(桶)与销售单价(元)的函数关系式为:
(2)由题意,得:
答:该经营部希望日均获利1200元,求该桶装水的销售单价为8元.
16.(1)
(2)116.16万元
(1)解:设今、明两年新能源汽车数量的平均增长率为,
由题意,得,
解得,,(舍去),
答:今、明两年新能源汽车数量的平均增长率为;
(2)解:(万元),
答:该市财政部门今年需要准备116.16万元补贴资金.
17.
解:设道路的宽为,根据题意得:
,
解得:,(不合题意,舍去),
答:道路的宽为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
