12.2.1全等三角形的判定SSS 同步巩固练 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 12.2.1全等三角形的判定SSS 同步巩固练 2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
12.2.1全等三角形的判定SSS 同步巩固练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.如图,中,,,直接使用“”可判定( )
A. B.
C. D.
2.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.如图,交于点O,则下列结论不正确的是( )
A. B.
C. D.
4.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
5.如图已知,,点B,D,E,C在同一条直线上,要利用“”,推理出还需要添加的一个条件可以是( )
A. B. C. D.以上都对
6.如图,用直尺和圆规作,作图痕迹中,弧是( )
A.以点C为圆心,为半径的弧 B.以点C为圆心,为半径的弧
C.以点G为圆心,为半径的弧 D.以点G为圆心,为半径的弧
7.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个(不含△ABC)
A.28 B.29 C.30 D.31
8.下列各命题都成立,逆命题也成立的有( )
(1)同旁内角互补,两直线平行 (2)全等三角形的对应边相等
(3)如果两个角是直角,那么它们相等 (4)如果两个实数相等,那么它们的平方相等
A.1个 B.2个 C.3个 D.4个
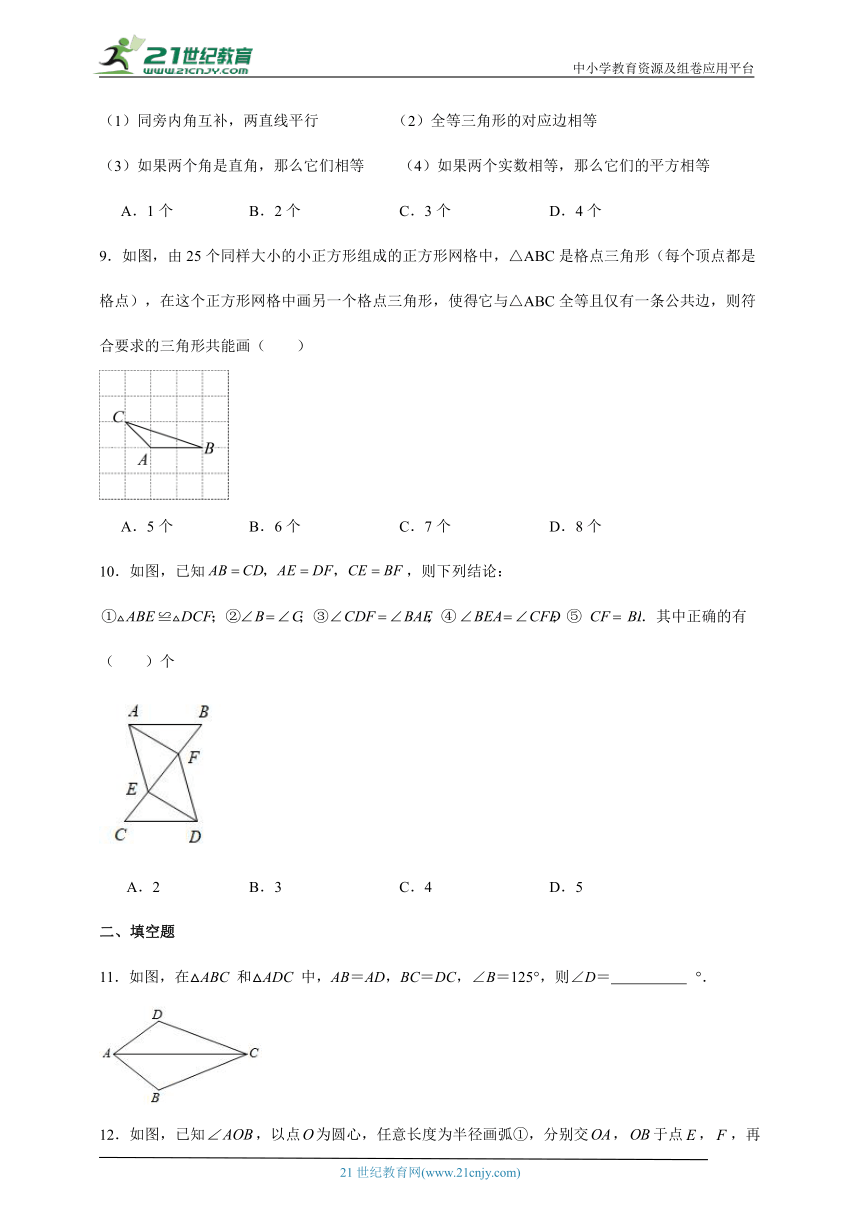
9.如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
A.5个 B.6个 C.7个 D.8个
10.如图,已知,则下列结论:.其中正确的有( )个
A.2 B.3 C.4 D.5
二、填空题
11.如图,在△ABC 和△ADC 中,AB=AD,BC=DC,∠B=125°,则∠D= °.
12.如图,已知,以点为圆心,任意长度为半径画弧①,分别交,于点,,再以点为圆心,的长为半径画弧,交弧①于点,画射线.若,则的度数为 .
13.如图,AB=CB,AD=CD 根据 可得到△ABD △CBD.
14.如图,AB=AC,BE=CD,要使,依据SSS,则还需添加条件 .(填一个即可)
15.如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是 .
三、解答题
16.如图,已知,,.
(1)求证:;
(2)猜想,,之间的数量关系,并证明.
17.如图,在和中,,,.
(1)求证:.
(2)若,,求的长.
参考答案:
1.C
解:∵,,,
∴,
根据现有条件无法直接利用判定,,,
2.C
解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
3.C
解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
4.C
解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
5.B
解:当时,,
理由:∵,
又,,
∴()
6.D
解:由图可得,
∵用尺规作出了,
∴弧是以点G为圆心,为半径的弧,
7.D
解:每个的正方形中可以画出8个与△ABC全等的格点三角形,
图中的正方形包含有4个的正方形,
∴与△ABC全等的格点三角形的个数有:4×8-1=31个.
8.B
解:(1)其逆命题是两直线平行,同旁内角互补,成立;
(2)其逆命题是对应边相等的两个三角形全等,成立;
(3)其逆命题是如果两个角相等,那么它们是直角,不成立;
(4)其逆命题是如果两个实数的平方相等,那么这两个实数相等,不成立;
故(1)(2)共2个的逆命题成立,
9.B
如图,
∵△ABC≌△GCB≌△BAW≌△CDA≌△AEC≌△ABQ≌△ABF,
∴与△ABC全等且仅有1条公共边的三角形共6个,
10.D
解:∵,
∴,
即,
在和中,
,
∴,
∴,
故正确,
11.125
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠B=∠D=125°.
故答案为:125.
12./26度
解:根据作图过程可知:
,,
∴,
∴.
故答案为:.
13. SSS ≌
解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
14.或(填其中任一个均可)
由题意,有以下两种情况:
(1)当时,由定理可证得;
(2)当时,
,
,即,
则当时,也可利用定理证得;
故答案为:或(填其中任一个均可).
15.(﹣2,3)或(﹣2,﹣3)或(0,﹣3)
如图所示,△BCD与△ABC全等,点D的坐标可以是(﹣2,3)或(﹣2,﹣3)或(0,﹣3).
故答案为: (﹣2,3)或(﹣2,﹣3)或(0,﹣3)
16.(1)证明见解析;
(2),理由见解析.
(1)证明:在和中,
,
∴,
∴,
∴,
∴;
(2),理由如下:
由()得:,
∴,
∵,
∴.
17.(1)见解析
(2)
(1)证明: ,
,
即,
在和中
,
().
(2)解:,,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.2.1全等三角形的判定SSS 同步巩固练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.如图,中,,,直接使用“”可判定( )
A. B.
C. D.
2.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
3.如图,交于点O,则下列结论不正确的是( )
A. B.
C. D.
4.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
5.如图已知,,点B,D,E,C在同一条直线上,要利用“”,推理出还需要添加的一个条件可以是( )
A. B. C. D.以上都对
6.如图,用直尺和圆规作,作图痕迹中,弧是( )
A.以点C为圆心,为半径的弧 B.以点C为圆心,为半径的弧
C.以点G为圆心,为半径的弧 D.以点G为圆心,为半径的弧
7.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个(不含△ABC)
A.28 B.29 C.30 D.31
8.下列各命题都成立,逆命题也成立的有( )
(1)同旁内角互补,两直线平行 (2)全等三角形的对应边相等
(3)如果两个角是直角,那么它们相等 (4)如果两个实数相等,那么它们的平方相等
A.1个 B.2个 C.3个 D.4个
9.如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
A.5个 B.6个 C.7个 D.8个
10.如图,已知,则下列结论:.其中正确的有( )个
A.2 B.3 C.4 D.5
二、填空题
11.如图,在△ABC 和△ADC 中,AB=AD,BC=DC,∠B=125°,则∠D= °.
12.如图,已知,以点为圆心,任意长度为半径画弧①,分别交,于点,,再以点为圆心,的长为半径画弧,交弧①于点,画射线.若,则的度数为 .
13.如图,AB=CB,AD=CD 根据 可得到△ABD △CBD.
14.如图,AB=AC,BE=CD,要使,依据SSS,则还需添加条件 .(填一个即可)
15.如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是 .
三、解答题
16.如图,已知,,.
(1)求证:;
(2)猜想,,之间的数量关系,并证明.
17.如图,在和中,,,.
(1)求证:.
(2)若,,求的长.
参考答案:
1.C
解:∵,,,
∴,
根据现有条件无法直接利用判定,,,
2.C
解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
3.C
解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
4.C
解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
5.B
解:当时,,
理由:∵,
又,,
∴()
6.D
解:由图可得,
∵用尺规作出了,
∴弧是以点G为圆心,为半径的弧,
7.D
解:每个的正方形中可以画出8个与△ABC全等的格点三角形,
图中的正方形包含有4个的正方形,
∴与△ABC全等的格点三角形的个数有:4×8-1=31个.
8.B
解:(1)其逆命题是两直线平行,同旁内角互补,成立;
(2)其逆命题是对应边相等的两个三角形全等,成立;
(3)其逆命题是如果两个角相等,那么它们是直角,不成立;
(4)其逆命题是如果两个实数的平方相等,那么这两个实数相等,不成立;
故(1)(2)共2个的逆命题成立,
9.B
如图,
∵△ABC≌△GCB≌△BAW≌△CDA≌△AEC≌△ABQ≌△ABF,
∴与△ABC全等且仅有1条公共边的三角形共6个,
10.D
解:∵,
∴,
即,
在和中,
,
∴,
∴,
故正确,
11.125
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠B=∠D=125°.
故答案为:125.
12./26度
解:根据作图过程可知:
,,
∴,
∴.
故答案为:.
13. SSS ≌
解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
14.或(填其中任一个均可)
由题意,有以下两种情况:
(1)当时,由定理可证得;
(2)当时,
,
,即,
则当时,也可利用定理证得;
故答案为:或(填其中任一个均可).
15.(﹣2,3)或(﹣2,﹣3)或(0,﹣3)
如图所示,△BCD与△ABC全等,点D的坐标可以是(﹣2,3)或(﹣2,﹣3)或(0,﹣3).
故答案为: (﹣2,3)或(﹣2,﹣3)或(0,﹣3)
16.(1)证明见解析;
(2),理由见解析.
(1)证明:在和中,
,
∴,
∴,
∴,
∴;
(2),理由如下:
由()得:,
∴,
∵,
∴.
17.(1)见解析
(2)
(1)证明: ,
,
即,
在和中
,
().
(2)解:,,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
