第十一章 11.2.2 三角形的外角 重点练 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 第十一章 11.2.2 三角形的外角 重点练 2024--2025学年上学期初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1009.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 15:00:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.2.2 三角形的外角 重点练
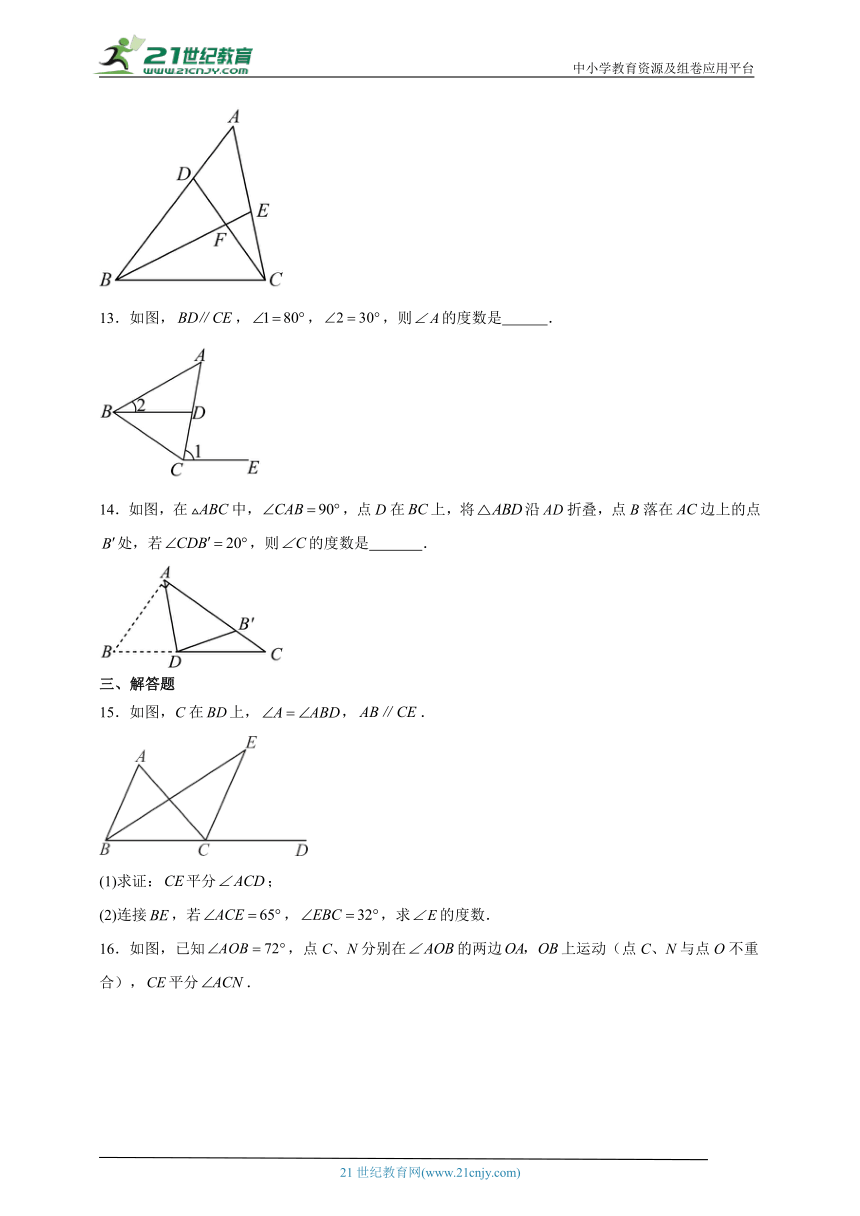
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.如图,中,,则三角形的外角等于( )
A. B. C. D.
2.如图,是的外角的平分线,且交的延长线于点,已知,,则的大小为( )
A. B. C. D.
3.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点,若,则的度数为( )
A. B. C. D.
4.如图,已知长方形纸片, 点 、 在 边上,点、 在 边上,分别沿、 折叠,使点 和点 都落在点 处,若,则 的度数为( )
A. B. C. D.
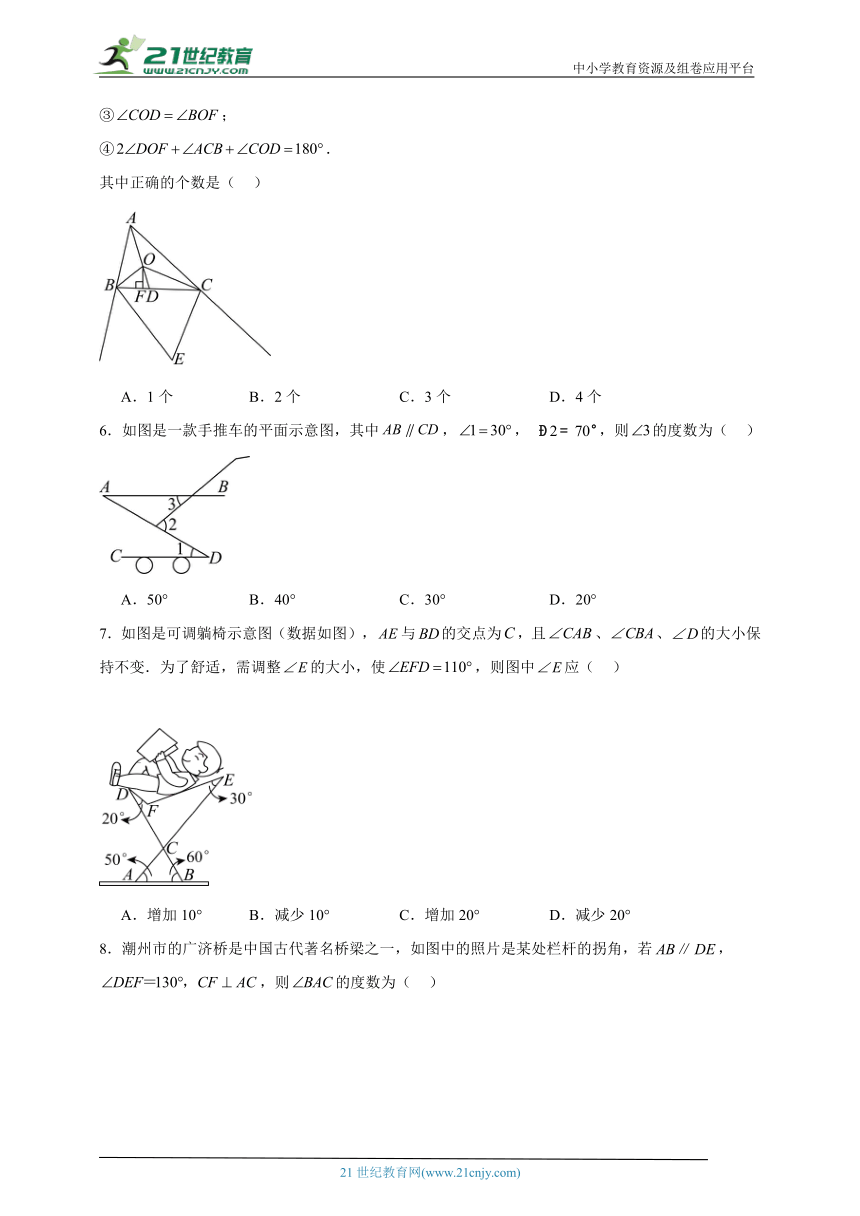
5.如图,在中,、分别平分和,连接并延长交于点,于点,、是外角平分线,现给出下列结论:
①平分;
②与互补;
③;
④.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图是一款手推车的平面示意图,其中,, ,则的度数为( )
A.50° B.40° C.30° D.20°
7.如图是可调躺椅示意图(数据如图),与的交点为,且、、的大小保持不变.为了舒适,需调整的大小,使,则图中应( )
A.增加10° B.减少10° C.增加20° D.减少20°
8.潮州市的广济桥是中国古代著名桥梁之一,如图中的照片是某处栏杆的拐角,若,,则的度数为( )
A. B. C. D.
二、填空题
9.将一副三角板如图摆放,顶点在边上,顶点在边上,,则的度数为 .
10.在中,的平分线与的平分线相交于点P.的外角平分线与的外角平分线相交于点Q,当,则 °;
11.如图,在中,,将沿着直线折叠,点在落点的位置,则的大小是 度.
12.如图,是的角平分线,是边上一点,交于点.若,,则的度数为 .
13.如图,,,,则的度数是 .
14.如图,在中,,点D在上,将沿折叠,点B落在边上的点处,若,则的度数是 .
三、解答题
15.如图,C在上,,.
(1)求证:平分;
(2)连接,若,,求的度数.
16.如图,已知,点C、N分别在的两边上运动(点C、N与点O不重合),平分.
(1)若,试求出的度数;
(2)已知平分交的反向延长线于点F.在点C、N的运动过程中,的度数是否发生改变?若不变,试求出的度数;若发生改变,请说明理由.
17.如图,在中,是的平分线,,点D在的延长线上,.求:的度数.
18.如图,分别为的中线、高,点E为的中点.
(1)若求的度数;
(2)若的面积为15,求的长.
参考答案:
1.B
解:中,,
,
2.C
解:∵,是的外角,
∴,
∵平分,
∴,
∵是的外角,
∴.
3.B
解:根据题意得:,
,
,
4.A
解:∵长方形,
∴,
∴,
∵分别沿,折叠,使点和点都落在点处,
∴,
∴,
∵,,
∴,
∴,
∴,
5.C
解:将图按照如下命名:
∵、分别平分和,
∴连接并延长交于点,则为的平分线,
∴①正确,
∵、分别平分和,
∴,,
∵、是外角平分线,
∴,,
∵,,
∴,,
∵四边形内角和为,
∴,
∴与互补,即②正确,
∵,
∵,,,
,
∴,
∴,
∴,即③正确,
∵,,
∴,
∴,
∴,
∴,
∴④不正确,
6.B
解:∵,,
∴,
∵,
,
∴
7.B
解:延长,交于点,如图:
,
.
,
.
,,
.
而图中,
应减少.
8.C
解:∵,,
∴,
又∵,,
∴.
9./度
解:根据三角板特征可得:,,,
,
,
,
,
是的外角,
.
故答案为:.
10.115
解:∵,
∴,,
∵的平分线与的平分线相交于点,
,
,
由三角形外角性质得:,
,
,
,
∵的平分线与的平分线相交于点,
,
,
,
故答案为:115.
11.80
解:如图,
由折叠得,,
∵,
∴,
∴,得,
∴,
∵,即,
∴,
∵,
∴
∴
故答案为80.
12.
解:是的外角,
,
,
又,
,
是的角平分线,
,
是的外角,
,
是的外角,
,
,
在中,,
,即,
,
故答案为:.
13./50度
∵,,
∴,
又∵,,
∴,
故答案为:.
14./35度
∵将沿折叠,点B落在边上的点处,
∴,,
∵,
∴,
∵,,
∴,
∴,
故答案为:.
15.(1)证明见解析
(2)
(1)证明:∵,
∴,,
∵,
∴,
∴平分;
(2)∵平分,
∴,
∵,
∴.
16.(1)
(2)不变,
(1)解:∵,,
∴,
∵,,
∴;
(2)的度数不变,
理由如下:如图所示,
∵平分,平分,
∴,,
∵ ,
∴,
∵ ,
∴,
∵ ,
∴.
17.
解:∵,
∴,
又平分,
∴,
又,
∴.
18.(1)
(2)
(1)解:∵
∴,
∵是的高线,
∴,
∴;
(2)∵的面积为15,点E为的中点,
∴,
∵,,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.2.2 三角形的外角 重点练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.如图,中,,则三角形的外角等于( )
A. B. C. D.
2.如图,是的外角的平分线,且交的延长线于点,已知,,则的大小为( )
A. B. C. D.
3.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点,若,则的度数为( )
A. B. C. D.
4.如图,已知长方形纸片, 点 、 在 边上,点、 在 边上,分别沿、 折叠,使点 和点 都落在点 处,若,则 的度数为( )
A. B. C. D.
5.如图,在中,、分别平分和,连接并延长交于点,于点,、是外角平分线,现给出下列结论:
①平分;
②与互补;
③;
④.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图是一款手推车的平面示意图,其中,, ,则的度数为( )
A.50° B.40° C.30° D.20°
7.如图是可调躺椅示意图(数据如图),与的交点为,且、、的大小保持不变.为了舒适,需调整的大小,使,则图中应( )
A.增加10° B.减少10° C.增加20° D.减少20°
8.潮州市的广济桥是中国古代著名桥梁之一,如图中的照片是某处栏杆的拐角,若,,则的度数为( )
A. B. C. D.
二、填空题
9.将一副三角板如图摆放,顶点在边上,顶点在边上,,则的度数为 .
10.在中,的平分线与的平分线相交于点P.的外角平分线与的外角平分线相交于点Q,当,则 °;
11.如图,在中,,将沿着直线折叠,点在落点的位置,则的大小是 度.
12.如图,是的角平分线,是边上一点,交于点.若,,则的度数为 .
13.如图,,,,则的度数是 .
14.如图,在中,,点D在上,将沿折叠,点B落在边上的点处,若,则的度数是 .
三、解答题
15.如图,C在上,,.
(1)求证:平分;
(2)连接,若,,求的度数.
16.如图,已知,点C、N分别在的两边上运动(点C、N与点O不重合),平分.
(1)若,试求出的度数;
(2)已知平分交的反向延长线于点F.在点C、N的运动过程中,的度数是否发生改变?若不变,试求出的度数;若发生改变,请说明理由.
17.如图,在中,是的平分线,,点D在的延长线上,.求:的度数.
18.如图,分别为的中线、高,点E为的中点.
(1)若求的度数;
(2)若的面积为15,求的长.
参考答案:
1.B
解:中,,
,
2.C
解:∵,是的外角,
∴,
∵平分,
∴,
∵是的外角,
∴.
3.B
解:根据题意得:,
,
,
4.A
解:∵长方形,
∴,
∴,
∵分别沿,折叠,使点和点都落在点处,
∴,
∴,
∵,,
∴,
∴,
∴,
5.C
解:将图按照如下命名:
∵、分别平分和,
∴连接并延长交于点,则为的平分线,
∴①正确,
∵、分别平分和,
∴,,
∵、是外角平分线,
∴,,
∵,,
∴,,
∵四边形内角和为,
∴,
∴与互补,即②正确,
∵,
∵,,,
,
∴,
∴,
∴,即③正确,
∵,,
∴,
∴,
∴,
∴,
∴④不正确,
6.B
解:∵,,
∴,
∵,
,
∴
7.B
解:延长,交于点,如图:
,
.
,
.
,,
.
而图中,
应减少.
8.C
解:∵,,
∴,
又∵,,
∴.
9./度
解:根据三角板特征可得:,,,
,
,
,
,
是的外角,
.
故答案为:.
10.115
解:∵,
∴,,
∵的平分线与的平分线相交于点,
,
,
由三角形外角性质得:,
,
,
,
∵的平分线与的平分线相交于点,
,
,
,
故答案为:115.
11.80
解:如图,
由折叠得,,
∵,
∴,
∴,得,
∴,
∵,即,
∴,
∵,
∴
∴
故答案为80.
12.
解:是的外角,
,
,
又,
,
是的角平分线,
,
是的外角,
,
是的外角,
,
,
在中,,
,即,
,
故答案为:.
13./50度
∵,,
∴,
又∵,,
∴,
故答案为:.
14./35度
∵将沿折叠,点B落在边上的点处,
∴,,
∵,
∴,
∵,,
∴,
∴,
故答案为:.
15.(1)证明见解析
(2)
(1)证明:∵,
∴,,
∵,
∴,
∴平分;
(2)∵平分,
∴,
∵,
∴.
16.(1)
(2)不变,
(1)解:∵,,
∴,
∵,,
∴;
(2)的度数不变,
理由如下:如图所示,
∵平分,平分,
∴,,
∵ ,
∴,
∵ ,
∴,
∵ ,
∴.
17.
解:∵,
∴,
又平分,
∴,
又,
∴.
18.(1)
(2)
(1)解:∵
∴,
∵是的高线,
∴,
∴;
(2)∵的面积为15,点E为的中点,
∴,
∵,,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
