第十一章 11.3.2 多边形的内角和 同步检测题 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 第十一章 11.3.2 多边形的内角和 同步检测题 2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.3.2 多边形的内角和 同步检测题
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.八边形的内角和为( )
A. B. C. D.
2.一个多边形内角和是,则这个多边形的边数为( )
A.8 B.9 C.10 D.11
3.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为( )
A.9 B.10 C.11 D.以上均有可能
4.在某广场整修工程中,计划采用同一种正多边形地板砖铺设地面.则下列满足要求的地板砖是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
5.如图,五边形是正五边形,,若,则的度数为( )
A. B. C. D.
6.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2018°,则n等于( )
A.11 B.12 C.13 D.14
7.一个多边形截取一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是( )
A. B. C. D.以上都有可能
8.如果一个正多边形的每个外角是,则这个正多边形的对角线共有( )条.
A.8 B.9 C. D.
二、填空题
9.一个正多边形的内角和为,则这个正多边形的每一个外角等于 度.
10.一个正多边形每个内角与它相邻外角的度数比为,则这个正多边形的边数为 .
11.如图,在四边形纸片中,,若沿图中虚线剪去,则 °.
12.一个多边形截去一个角后,所形成的另一个多边形的内角和是2160°,则原多边形的边数是 .
13.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是 .
14.已知一个多边形除一个内角外其余内角的和为,则这个内角的度数为 .
三、解答题
15.一个多边形的所有内角与它的所有外角之和是.
(1)求该多边形的边数.
(2)若该多边形为正多边形,求每一个外角的度数.
16.如图,在四边形中,分别为的平分线,且,求的度数.
17.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
参考答案:
1.C
解:八边形的内角和为,
2.B
解:根据题意得:,
解得:.
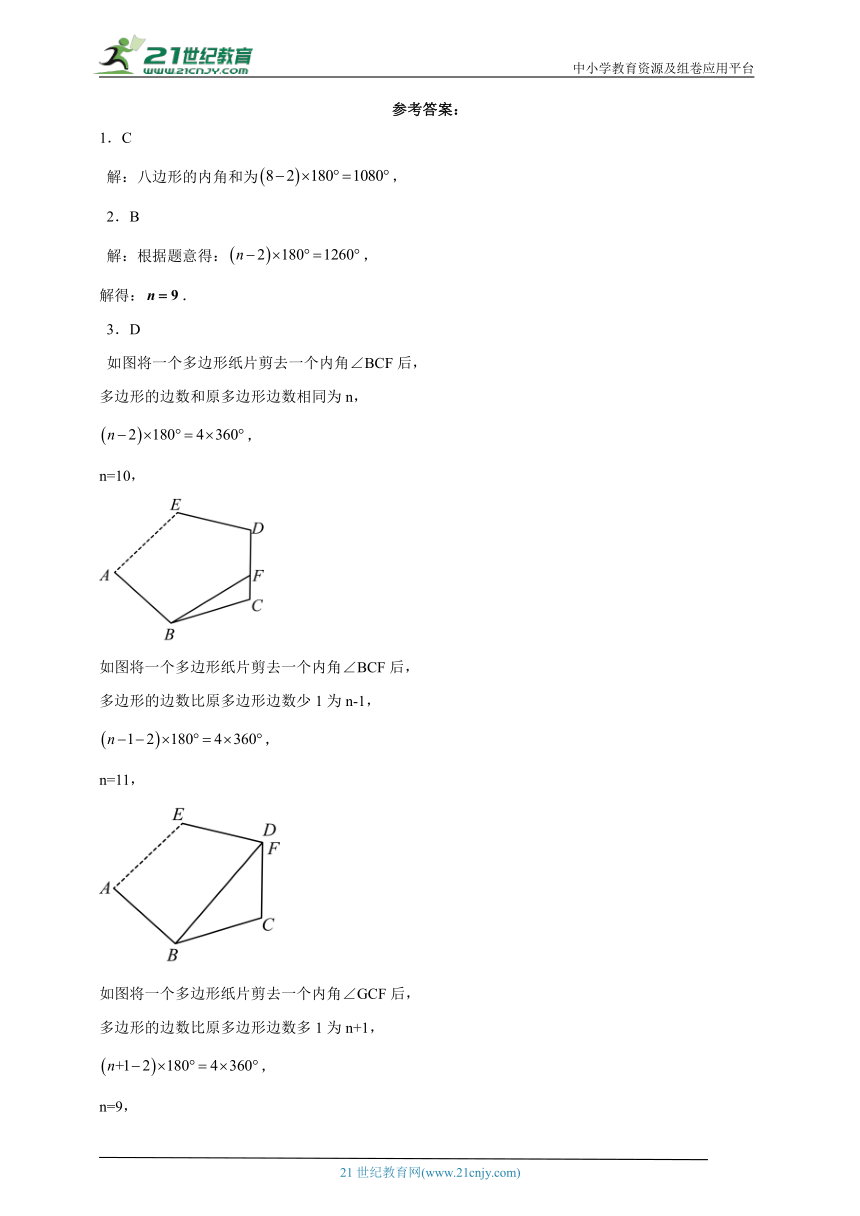
3.D
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数和原多边形边数相同为n,
,
n=10,
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数比原多边形边数少1为n-1,
,
n=11,
如图将一个多边形纸片剪去一个内角∠GCF后,
多边形的边数比原多边形边数多1为n+1,
,
n=9,
原多边形的边数为9,10,11.
4.B
解:∵用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,
∴用同一种正多边形铺满地面,则可供选择的正多边形是正六边形.
5.C
如图, 连接,
∵五边形是正五边形,
,,
,
,
,
6.C
解:设多输入的内角为(),由题意得
,
解得:,
为正整数,
当时,
;
7.D
解:设剪去一个角后的多边形边数为,根据题意得,
∴ 即得到的多边形是边形,
当沿的是一条对角线剪去一个角,则原来的是边形;
当沿的直线并不是对角线时,分为两种情况:
过多边形的一个顶点,则原来的是边形;
不过多边形的顶点,则原来的是边形,
∴原来多边形的边数可能是或或,
8.B
解:这个正多边形的边数:,
则对角线的条数是:,
9.72
解:设正多边形的边数为,根据题意得:
,
解得:,
∵正多边形的每个外角都相等,且外角和为,
∴正多边形的每一个外角为:.
故答案为:72.
10.6
解:这个正多边形的外角为,
所以这个正多边形为,
即这个正多边形为正六边形,边数为6,
11.
解:三角形的内角和等于,,
,.
,
.
故答案为:.
12.13或14或15
解:设多边形截去一个角的边数为n,根据题意得:
(n﹣2) 180°=2160°
解得:n=14.
∵截去一个角后边上可以增加1,不变,减少1,
∴原多边形的边数是13或14或15.
故答案为13或14或15.
13./度
解:∵,
∴少加的内角是:.
故答案为:.
14./80度
解:设这个多边形是边形,则其内角和为.
根据题意,得,
解得.
又n为正整数,故.
所以这个内角的度数为.
故答案为:.
另解:
因为多边形的内角和是的倍数,所以我们可以计算的余数,这个余数为,故加上刚好是的倍数,因此这个内角的度数为.
15.(1)7
(2)
(1)解:设该多边形的边数为,
由题意可得:,
解得:,
∴该多边形的边数为7;
(2)由(1)可得该多边形是正七边形,
每一个外角的度数.
16.
解:,,
.
分别为的平分线,
,
,
.
17.(1)八边形
(2)八边形
(1)解:设这个多边形是边形,
由题意得:,
解得,
答:这个多边形是八边形.
(2)解:设这个多边形是边形,重复加的一个角的度数为,则,
由题意得:,
解得,
则,即,
解得,
为正整数,
,
答:这个多边形是八边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.3.2 多边形的内角和 同步检测题
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.八边形的内角和为( )
A. B. C. D.
2.一个多边形内角和是,则这个多边形的边数为( )
A.8 B.9 C.10 D.11
3.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为( )
A.9 B.10 C.11 D.以上均有可能
4.在某广场整修工程中,计划采用同一种正多边形地板砖铺设地面.则下列满足要求的地板砖是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
5.如图,五边形是正五边形,,若,则的度数为( )
A. B. C. D.
6.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2018°,则n等于( )
A.11 B.12 C.13 D.14
7.一个多边形截取一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是( )
A. B. C. D.以上都有可能
8.如果一个正多边形的每个外角是,则这个正多边形的对角线共有( )条.
A.8 B.9 C. D.
二、填空题
9.一个正多边形的内角和为,则这个正多边形的每一个外角等于 度.
10.一个正多边形每个内角与它相邻外角的度数比为,则这个正多边形的边数为 .
11.如图,在四边形纸片中,,若沿图中虚线剪去,则 °.
12.一个多边形截去一个角后,所形成的另一个多边形的内角和是2160°,则原多边形的边数是 .
13.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是 .
14.已知一个多边形除一个内角外其余内角的和为,则这个内角的度数为 .
三、解答题
15.一个多边形的所有内角与它的所有外角之和是.
(1)求该多边形的边数.
(2)若该多边形为正多边形,求每一个外角的度数.
16.如图,在四边形中,分别为的平分线,且,求的度数.
17.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
参考答案:
1.C
解:八边形的内角和为,
2.B
解:根据题意得:,
解得:.
3.D
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数和原多边形边数相同为n,
,
n=10,
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数比原多边形边数少1为n-1,
,
n=11,
如图将一个多边形纸片剪去一个内角∠GCF后,
多边形的边数比原多边形边数多1为n+1,
,
n=9,
原多边形的边数为9,10,11.
4.B
解:∵用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,
∴用同一种正多边形铺满地面,则可供选择的正多边形是正六边形.
5.C
如图, 连接,
∵五边形是正五边形,
,,
,
,
,
6.C
解:设多输入的内角为(),由题意得
,
解得:,
为正整数,
当时,
;
7.D
解:设剪去一个角后的多边形边数为,根据题意得,
∴ 即得到的多边形是边形,
当沿的是一条对角线剪去一个角,则原来的是边形;
当沿的直线并不是对角线时,分为两种情况:
过多边形的一个顶点,则原来的是边形;
不过多边形的顶点,则原来的是边形,
∴原来多边形的边数可能是或或,
8.B
解:这个正多边形的边数:,
则对角线的条数是:,
9.72
解:设正多边形的边数为,根据题意得:
,
解得:,
∵正多边形的每个外角都相等,且外角和为,
∴正多边形的每一个外角为:.
故答案为:72.
10.6
解:这个正多边形的外角为,
所以这个正多边形为,
即这个正多边形为正六边形,边数为6,
11.
解:三角形的内角和等于,,
,.
,
.
故答案为:.
12.13或14或15
解:设多边形截去一个角的边数为n,根据题意得:
(n﹣2) 180°=2160°
解得:n=14.
∵截去一个角后边上可以增加1,不变,减少1,
∴原多边形的边数是13或14或15.
故答案为13或14或15.
13./度
解:∵,
∴少加的内角是:.
故答案为:.
14./80度
解:设这个多边形是边形,则其内角和为.
根据题意,得,
解得.
又n为正整数,故.
所以这个内角的度数为.
故答案为:.
另解:
因为多边形的内角和是的倍数,所以我们可以计算的余数,这个余数为,故加上刚好是的倍数,因此这个内角的度数为.
15.(1)7
(2)
(1)解:设该多边形的边数为,
由题意可得:,
解得:,
∴该多边形的边数为7;
(2)由(1)可得该多边形是正七边形,
每一个外角的度数.
16.
解:,,
.
分别为的平分线,
,
,
.
17.(1)八边形
(2)八边形
(1)解:设这个多边形是边形,
由题意得:,
解得,
答:这个多边形是八边形.
(2)解:设这个多边形是边形,重复加的一个角的度数为,则,
由题意得:,
解得,
则,即,
解得,
为正整数,
,
答:这个多边形是八边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
