牛顿运动定律的应用(等时圆问题) 专项练 2025年高考物理一轮复习备考
文档属性
| 名称 | 牛顿运动定律的应用(等时圆问题) 专项练 2025年高考物理一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 764.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-11 16:17:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
牛顿运动定律的应用(等时圆问题) 专项练
2025年高考物理一轮复习备考
一、单选题
1.如图所示装置,位于竖直平面内的固定光滑圆轨道与水平轨道面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆轨道的圆心。已知在同一时刻,a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点;c球由C点自由下落到M点。则( )
A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.a、c、b三球依次先后到达M点
2.如图所示,在竖直平面内,固定一个半径为R的大圆环,其圆心为O,在圆内与圆心O同一水平面上的P点搭一光滑斜轨道到大环上,,欲使物体(视为质点)从P点由静止释放,沿此倾斜轨道滑到大环的时间最短,已知重力加速度为g,则( )
A.物体在光滑斜轨上滑行的加速度为
B.轨道长为
C.最短时间为
D.最短时间为
3.如图所示,倾角为的斜面固定在水平地面上,由斜面上方A点伸出三根光滑轻杆至斜面上BCD三点,其中轻杆AC与斜面垂直,,把可看成质点的质量为m的圆环依次沿三根轻杆从A点由静止滑下,滑到斜面过程中的平均速度分别为、、,下列说法正确的是( )
A. B. C. D.
4.如图所示,ad、bd、cd是竖直平面内三根固定的光滑细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为圆周的最低点。每根杆上都套着一个小滑环,三个滑环分别从a、b、c处释放(初速度都为0),用t1、t2、t3依次表示各滑环滑到d的时间,则( )
A. B.
C. D.
5.如图所示,竖直平面内存在半径为R的大圆和半径为r的小圆,两个圆的公切线水平,有两条倾斜的光滑轨道,一条与大圆相交于A、B两点,A点为大圆的最高点,另一条轨道一端交于大圆的C点.另一端交于小圆的D点,且过大圆和小圆的公切点。现让一物体分别从两条轨道的顶端A、C由静止释放,分别滑到B点和D点(假设物体能够无障碍地穿过CD与圆的交叉点),物体在两条轨道上的运动时间分别为、,重力加速度为g,下列判断正确的是( )
A. B.
C. D.
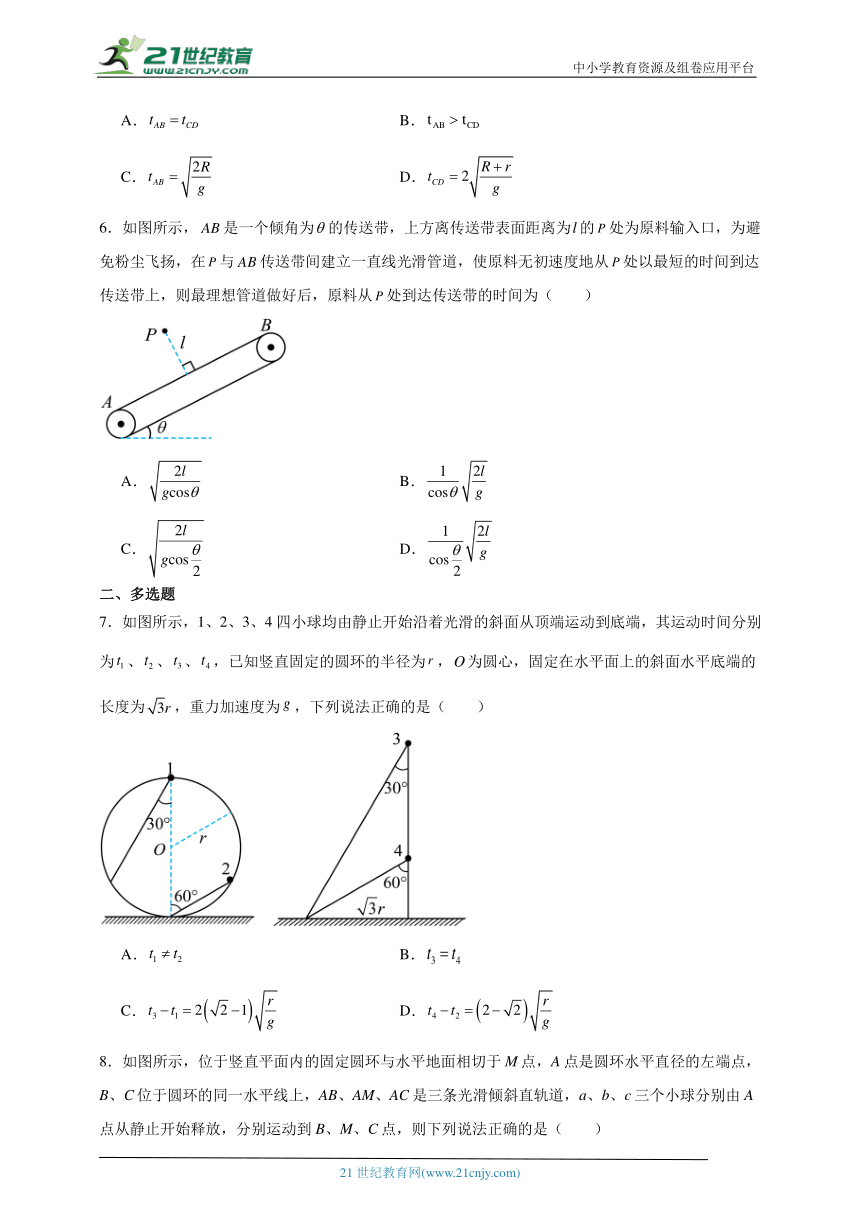
6.如图所示,是一个倾角为的传送带,上方离传送带表面距离为的处为原料输入口,为避免粉尘飞扬,在与传送带间建立一直线光滑管道,使原料无初速度地从处以最短的时间到达传送带上,则最理想管道做好后,原料从处到达传送带的时间为( )
A. B.
C. D.
二、多选题
7.如图所示,1、2、3、4四小球均由静止开始沿着光滑的斜面从顶端运动到底端,其运动时间分别为、、、,已知竖直固定的圆环的半径为,为圆心,固定在水平面上的斜面水平底端的长度为,重力加速度为,下列说法正确的是( )
A. B.
C. D.
8.如图所示,位于竖直平面内的固定圆环与水平地面相切于M点,A点是圆环水平直径的左端点,B、C位于圆环的同一水平线上,AB、AM、AC是三条光滑倾斜直轨道,a、b、c三个小球分别由A点从静止开始释放,分别运动到B、M、C点,则下列说法正确的是( )
A.球a运动到B点所用的时间最短 B.球b运动到M点所用的时间最长
C.球c运动到C点所用的时间最长 D.三球所用的时间一样长
9.如图所示,让物体同时从竖直圆上的P1、P2处由静止开始下滑,沿光滑的弦轨道P1A、P2A滑到A处,P1A、P2A与竖直直径的夹角分别为θ1、θ2则( )
A.物体沿P1A、P2A下滑加速度之比为sinθ1: sinθ2
B.物体沿P1A、P2A下滑到A处的速度之比为cosθ1: cosθ2
C.物体沿P1A、P2A下滑的时间之比为1:1
D.两物体质量相同,则两物体所受的合外力之比为cosθ1: cosθ2
三、解答题
10.滑滑梯是小朋友们爱玩的游戏。有两部直滑梯AB和AC,A、B、C在竖直平面内的同一圆周上,且A为圆周的最高点,示意图如图所示,已知圆周半径为R。在圆周所在的竖直平面内有一位置P,距离A点为R,且与A等高。各滑梯的摩擦均不计,已知重力加速度为g。
(1)如果小朋友由静止开始分别沿AB和AC滑下,试通过计算说明两次沿滑梯运动的时间关系;
(2)若设计一部上端在P点,下端在圆周上某点的直滑梯,则小朋友沿此滑梯由静止滑下时,在滑梯上运动的最短时间是多少。
11.如图甲所示, bc是竖直面内一根固定的光滑细杆,a、b、c位于同一圆周上,圆的半径为R,a点为圆周的最高点,c点为最低点。让一个小滑环从 b点由静止释放到达c 点;如图乙所示,在竖直平面内,固定一个半径为R的大圆环,其圆心为O,在圆内与圆心O同一水平面上的 P 点搭一光滑斜轨道到大环上,,欲使物体(视为质点)从 P 点由静止释放,沿此倾斜轨道滑到大环。已知重力加速度为 g。
(1)求小滑环从b点运动到c点的时间;
(2)求物体从 P 点滑到大环的最小时间。
参考答案:
1.C
设圆轨道半径为R,据“等时圆”理论
B点在圆外,有
tb>ta
C球做自由落体运动,有
tc=
故有
tc2.D
B.如图建立一个与大圆相内切的等时圆,如图所示。
设其半径为r,由几何关系得
解得
由等时圆可知,从P点运动到切点M为最短时间,由几何关系可知
则轨道长度
选项B错误;
CD.由等时圆可知从P到M的时间为
即最短时间为
选项C错误,D正确;
A.根据
可得
选项A错误。
3.B
因AB垂直于斜面底边,以AB为直径做圆,则必过C点,如图
圆环在杆AC上运动过程,由牛顿第二定律及运动学公式可得
联立解得
即从A点出发,到达圆周各点所用的时间相等,与杆的长短、倾角无关,可得
由平均速度
又因为
可得
圆环从A到C的平均速度
圆环从A到D的过程有
则平均速度
则可得
综上可得
4.D
设某光滑细杆与竖直方向的夹角为θ,其上一小环受到重力和杆的支持力作用,由牛顿第二定律得
据几何关系得细杆长度为
环在杆上由静止做匀加速运动,由运动学公式有
解得
由计算结果可知,环沿细杆下滑时间与杆的倾斜程度无关,即
5.D
设轨道与竖直方向的夹角为,则物体在轨道上运动的加速度大小为
根据运动学公式可得
解得
设轨道与竖直方向的夹角为,则物体在轨道上运动的加速度大小为
根据运动学公式可得
解得
则有
6.D
如图所示
以处为圆的最高点作圆与传送带相切于点,设圆的半径为,从处建立一管道到圆周上,管道与竖直方向的夹角为,原料下滑的加速度为
管道长度为
由运动学公式可得
解得
可知从处建立任一管道到圆周上,原料下滑的时间相等,故在与传送带间建立一管道,原料从处到传送带上所用时间最短;根据图中几何关系可得
可得
联立可得
7.BC
1号小球的加速度为
位移为
运动时间为
2号小球的加速度为
位移为
运动时间为
3号小球的加速度为
位移为
运动时间为
4号小球的加速度为
位移为
运动时间为
则
,
8.AC
设圆半径为R,从A点开始的倾斜直轨道与水平方向的夹角为,则小球下滑的加速度为
根据运动公式
解得
因越大,则时间越短,可知球a运动到B点所用的时间最短,球c运动到C点所用的时间最长。
9.BCD
A.物体受重力、支持力,根据牛顿第二定律
解得
物体沿P1A、P2A下滑加速度之比为
A错误;
B.末速度为
解得
速度之比为
B正确;
C.下滑的时间为
解得
下滑的时间之比为
C正确;
D.合外力之比为
D正确。
10.(1);(2)
(1)设AB与水平方向的夹角为θ,小朋友沿AB下滑时的加速度
由运动学公式有
由几何关系知
解得
由上式可知,沿滑梯运动的时间t与滑梯和水平面间的夹角无关,同理可知
故
(2)画出以P点为最高点、半径为r与题图中圆外切的圆,如图
设切点为D,根据第(1)问的结论,当小朋友沿滑梯PD下滑时,在滑梯上运动的时间最短,由几何关系知
解得
结合第(1)问的结论有
11.(1);(2)
(1)设ac与bc夹角为,则有
由几何关系得bc 细杆长度为
小滑环匀加速运动,根据运动学公式可得
联立解得
(2)如图建立一个与大圆相内切的等时圆
设其半径为,由几何关系得
解得
从 P 点运动到切点为最短时间,由(1)结论得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
牛顿运动定律的应用(等时圆问题) 专项练
2025年高考物理一轮复习备考
一、单选题
1.如图所示装置,位于竖直平面内的固定光滑圆轨道与水平轨道面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆轨道的圆心。已知在同一时刻,a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点;c球由C点自由下落到M点。则( )
A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.a、c、b三球依次先后到达M点
2.如图所示,在竖直平面内,固定一个半径为R的大圆环,其圆心为O,在圆内与圆心O同一水平面上的P点搭一光滑斜轨道到大环上,,欲使物体(视为质点)从P点由静止释放,沿此倾斜轨道滑到大环的时间最短,已知重力加速度为g,则( )
A.物体在光滑斜轨上滑行的加速度为
B.轨道长为
C.最短时间为
D.最短时间为
3.如图所示,倾角为的斜面固定在水平地面上,由斜面上方A点伸出三根光滑轻杆至斜面上BCD三点,其中轻杆AC与斜面垂直,,把可看成质点的质量为m的圆环依次沿三根轻杆从A点由静止滑下,滑到斜面过程中的平均速度分别为、、,下列说法正确的是( )
A. B. C. D.
4.如图所示,ad、bd、cd是竖直平面内三根固定的光滑细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为圆周的最低点。每根杆上都套着一个小滑环,三个滑环分别从a、b、c处释放(初速度都为0),用t1、t2、t3依次表示各滑环滑到d的时间,则( )
A. B.
C. D.
5.如图所示,竖直平面内存在半径为R的大圆和半径为r的小圆,两个圆的公切线水平,有两条倾斜的光滑轨道,一条与大圆相交于A、B两点,A点为大圆的最高点,另一条轨道一端交于大圆的C点.另一端交于小圆的D点,且过大圆和小圆的公切点。现让一物体分别从两条轨道的顶端A、C由静止释放,分别滑到B点和D点(假设物体能够无障碍地穿过CD与圆的交叉点),物体在两条轨道上的运动时间分别为、,重力加速度为g,下列判断正确的是( )
A. B.
C. D.
6.如图所示,是一个倾角为的传送带,上方离传送带表面距离为的处为原料输入口,为避免粉尘飞扬,在与传送带间建立一直线光滑管道,使原料无初速度地从处以最短的时间到达传送带上,则最理想管道做好后,原料从处到达传送带的时间为( )
A. B.
C. D.
二、多选题
7.如图所示,1、2、3、4四小球均由静止开始沿着光滑的斜面从顶端运动到底端,其运动时间分别为、、、,已知竖直固定的圆环的半径为,为圆心,固定在水平面上的斜面水平底端的长度为,重力加速度为,下列说法正确的是( )
A. B.
C. D.
8.如图所示,位于竖直平面内的固定圆环与水平地面相切于M点,A点是圆环水平直径的左端点,B、C位于圆环的同一水平线上,AB、AM、AC是三条光滑倾斜直轨道,a、b、c三个小球分别由A点从静止开始释放,分别运动到B、M、C点,则下列说法正确的是( )
A.球a运动到B点所用的时间最短 B.球b运动到M点所用的时间最长
C.球c运动到C点所用的时间最长 D.三球所用的时间一样长
9.如图所示,让物体同时从竖直圆上的P1、P2处由静止开始下滑,沿光滑的弦轨道P1A、P2A滑到A处,P1A、P2A与竖直直径的夹角分别为θ1、θ2则( )
A.物体沿P1A、P2A下滑加速度之比为sinθ1: sinθ2
B.物体沿P1A、P2A下滑到A处的速度之比为cosθ1: cosθ2
C.物体沿P1A、P2A下滑的时间之比为1:1
D.两物体质量相同,则两物体所受的合外力之比为cosθ1: cosθ2
三、解答题
10.滑滑梯是小朋友们爱玩的游戏。有两部直滑梯AB和AC,A、B、C在竖直平面内的同一圆周上,且A为圆周的最高点,示意图如图所示,已知圆周半径为R。在圆周所在的竖直平面内有一位置P,距离A点为R,且与A等高。各滑梯的摩擦均不计,已知重力加速度为g。
(1)如果小朋友由静止开始分别沿AB和AC滑下,试通过计算说明两次沿滑梯运动的时间关系;
(2)若设计一部上端在P点,下端在圆周上某点的直滑梯,则小朋友沿此滑梯由静止滑下时,在滑梯上运动的最短时间是多少。
11.如图甲所示, bc是竖直面内一根固定的光滑细杆,a、b、c位于同一圆周上,圆的半径为R,a点为圆周的最高点,c点为最低点。让一个小滑环从 b点由静止释放到达c 点;如图乙所示,在竖直平面内,固定一个半径为R的大圆环,其圆心为O,在圆内与圆心O同一水平面上的 P 点搭一光滑斜轨道到大环上,,欲使物体(视为质点)从 P 点由静止释放,沿此倾斜轨道滑到大环。已知重力加速度为 g。
(1)求小滑环从b点运动到c点的时间;
(2)求物体从 P 点滑到大环的最小时间。
参考答案:
1.C
设圆轨道半径为R,据“等时圆”理论
B点在圆外,有
tb>ta
C球做自由落体运动,有
tc=
故有
tc
B.如图建立一个与大圆相内切的等时圆,如图所示。
设其半径为r,由几何关系得
解得
由等时圆可知,从P点运动到切点M为最短时间,由几何关系可知
则轨道长度
选项B错误;
CD.由等时圆可知从P到M的时间为
即最短时间为
选项C错误,D正确;
A.根据
可得
选项A错误。
3.B
因AB垂直于斜面底边,以AB为直径做圆,则必过C点,如图
圆环在杆AC上运动过程,由牛顿第二定律及运动学公式可得
联立解得
即从A点出发,到达圆周各点所用的时间相等,与杆的长短、倾角无关,可得
由平均速度
又因为
可得
圆环从A到C的平均速度
圆环从A到D的过程有
则平均速度
则可得
综上可得
4.D
设某光滑细杆与竖直方向的夹角为θ,其上一小环受到重力和杆的支持力作用,由牛顿第二定律得
据几何关系得细杆长度为
环在杆上由静止做匀加速运动,由运动学公式有
解得
由计算结果可知,环沿细杆下滑时间与杆的倾斜程度无关,即
5.D
设轨道与竖直方向的夹角为,则物体在轨道上运动的加速度大小为
根据运动学公式可得
解得
设轨道与竖直方向的夹角为,则物体在轨道上运动的加速度大小为
根据运动学公式可得
解得
则有
6.D
如图所示
以处为圆的最高点作圆与传送带相切于点,设圆的半径为,从处建立一管道到圆周上,管道与竖直方向的夹角为,原料下滑的加速度为
管道长度为
由运动学公式可得
解得
可知从处建立任一管道到圆周上,原料下滑的时间相等,故在与传送带间建立一管道,原料从处到传送带上所用时间最短;根据图中几何关系可得
可得
联立可得
7.BC
1号小球的加速度为
位移为
运动时间为
2号小球的加速度为
位移为
运动时间为
3号小球的加速度为
位移为
运动时间为
4号小球的加速度为
位移为
运动时间为
则
,
8.AC
设圆半径为R,从A点开始的倾斜直轨道与水平方向的夹角为,则小球下滑的加速度为
根据运动公式
解得
因越大,则时间越短,可知球a运动到B点所用的时间最短,球c运动到C点所用的时间最长。
9.BCD
A.物体受重力、支持力,根据牛顿第二定律
解得
物体沿P1A、P2A下滑加速度之比为
A错误;
B.末速度为
解得
速度之比为
B正确;
C.下滑的时间为
解得
下滑的时间之比为
C正确;
D.合外力之比为
D正确。
10.(1);(2)
(1)设AB与水平方向的夹角为θ,小朋友沿AB下滑时的加速度
由运动学公式有
由几何关系知
解得
由上式可知,沿滑梯运动的时间t与滑梯和水平面间的夹角无关,同理可知
故
(2)画出以P点为最高点、半径为r与题图中圆外切的圆,如图
设切点为D,根据第(1)问的结论,当小朋友沿滑梯PD下滑时,在滑梯上运动的时间最短,由几何关系知
解得
结合第(1)问的结论有
11.(1);(2)
(1)设ac与bc夹角为,则有
由几何关系得bc 细杆长度为
小滑环匀加速运动,根据运动学公式可得
联立解得
(2)如图建立一个与大圆相内切的等时圆
设其半径为,由几何关系得
解得
从 P 点运动到切点为最短时间,由(1)结论得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
