人教版2024年八年级上册第11-13章阶段性基础提升练习 含答案
文档属性
| 名称 | 人教版2024年八年级上册第11-13章阶段性基础提升练习 含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 21:14:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2024年八年级上册第11-13章阶段性基础提升练习
一.选择题
1.以下列各组线段为边,能组成三角形的是( )
A.2、2、4 B.8、6、3 C.2、6、3 D.11、4、6
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是( )
A.七 B.八 C.九 D.十
4.若图中的两个三角形全等,则依据所标数据可得( )
A.α=50° B.α=60° C.x=18 D.x=20
5.如图,AB⊥BC于B,DE⊥AC于E,AB=CE,AC=CD.则△ABC≌△CED的理由是( )
A.SSS B.SAS C.ASA D.HL
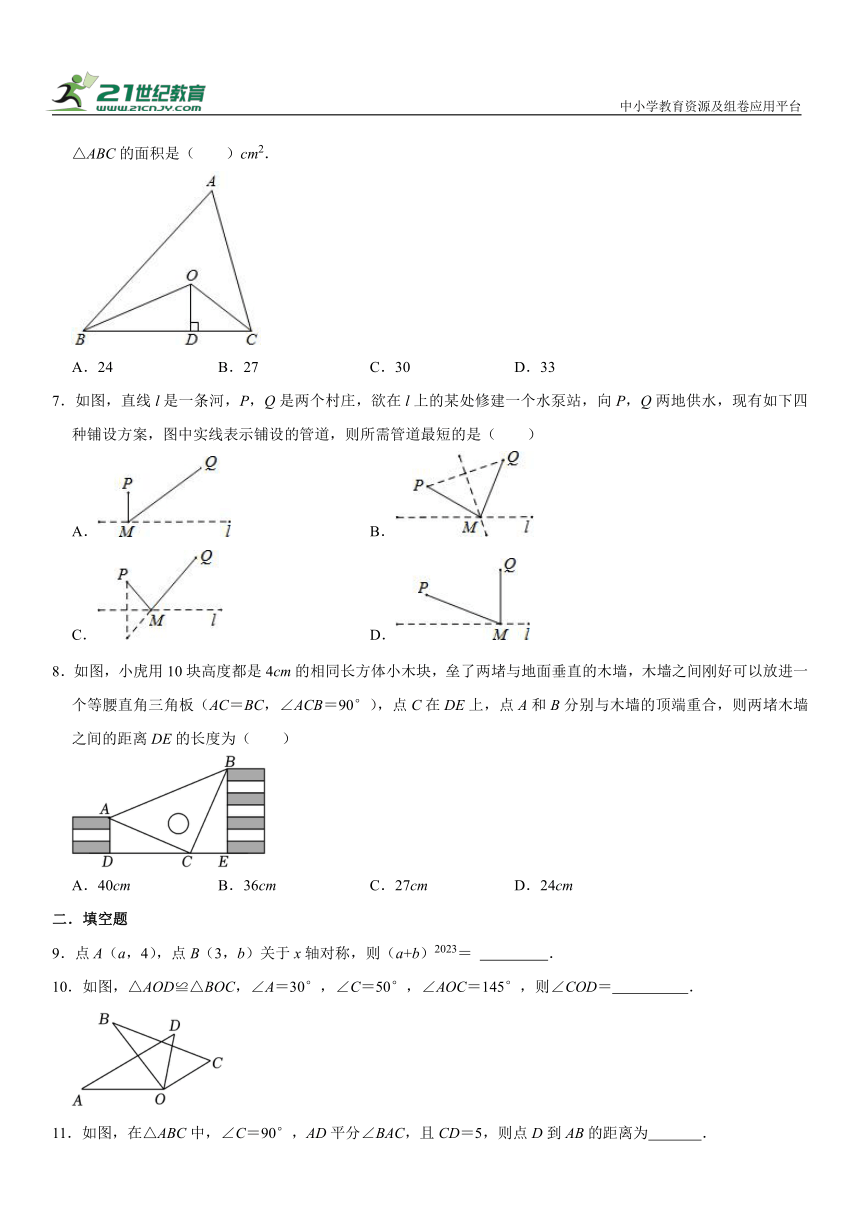
6.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
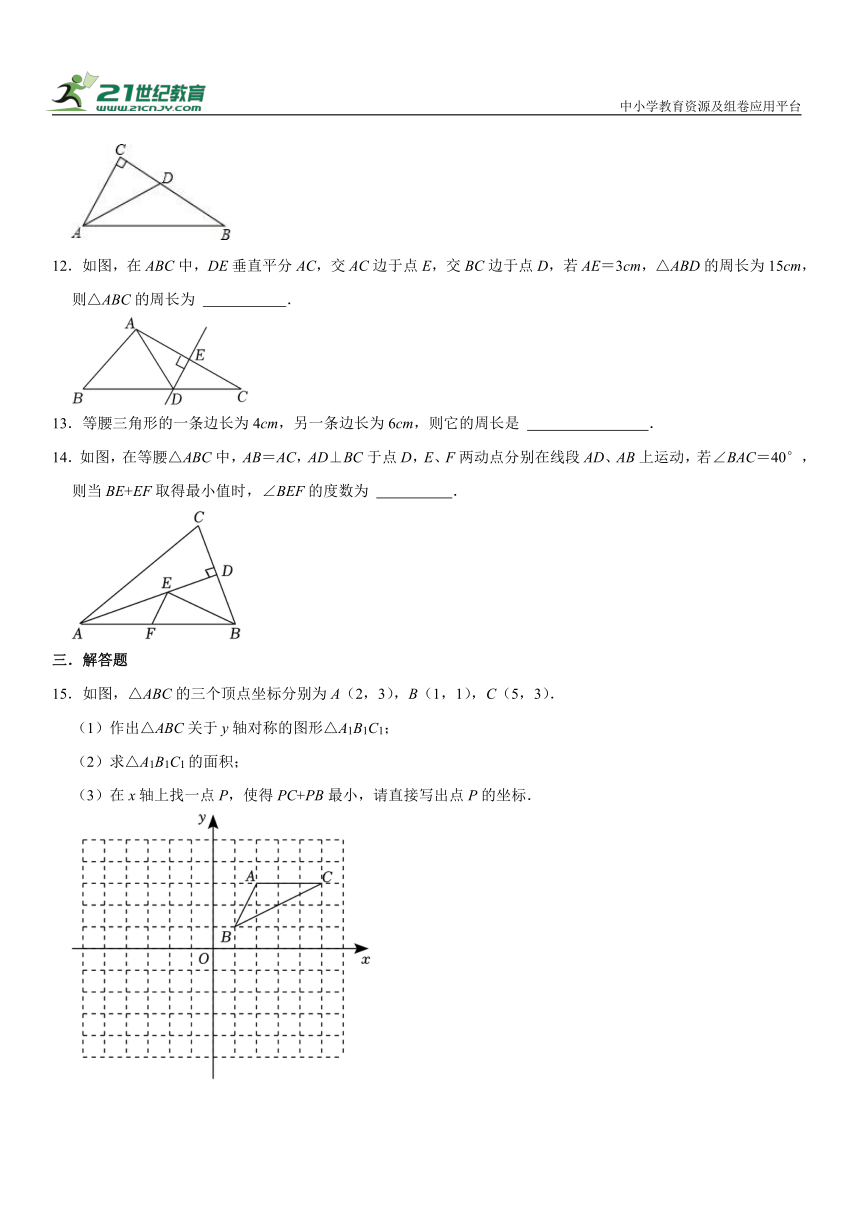
7.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
A. B.
C. D.
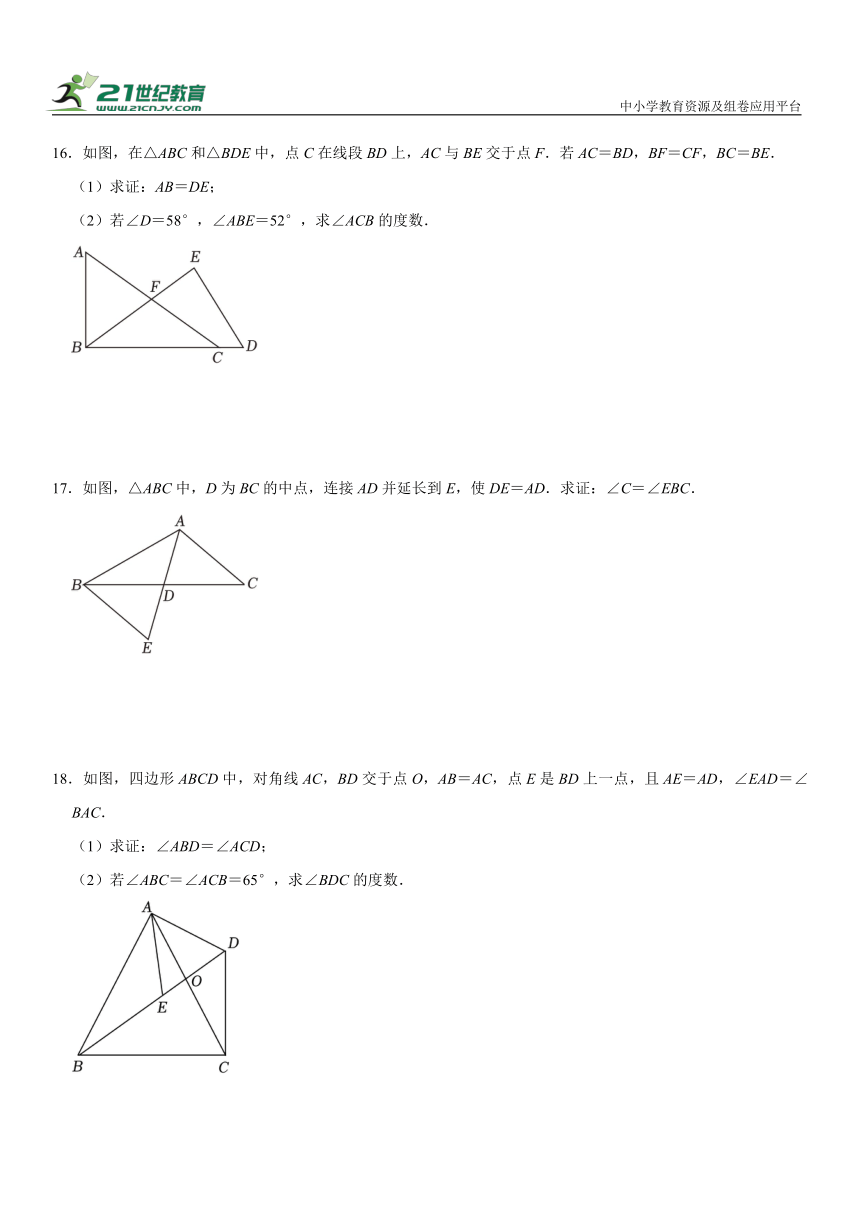
8.如图,小虎用10块高度都是4cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离DE的长度为( )
A.40cm B.36cm C.27cm D.24cm
二.填空题
9.点A(a,4),点B(3,b)关于x轴对称,则(a+b)2023= .
10.如图,△AOD≌△BOC,∠A=30°,∠C=50°,∠AOC=145°,则∠COD= .
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,且CD=5,则点D到AB的距离为 .
12.如图,在ABC中,DE垂直平分AC,交AC边于点E,交BC边于点D,若AE=3cm,△ABD的周长为15cm,则△ABC的周长为 .
13.等腰三角形的一条边长为4cm,另一条边长为6cm,则它的周长是 .
14.如图,在等腰△ABC中,AB=AC,AD⊥BC于点D,E、F两动点分别在线段AD、AB上运动,若∠BAC=40°,则当BE+EF取得最小值时,∠BEF的度数为 .
三.解答题
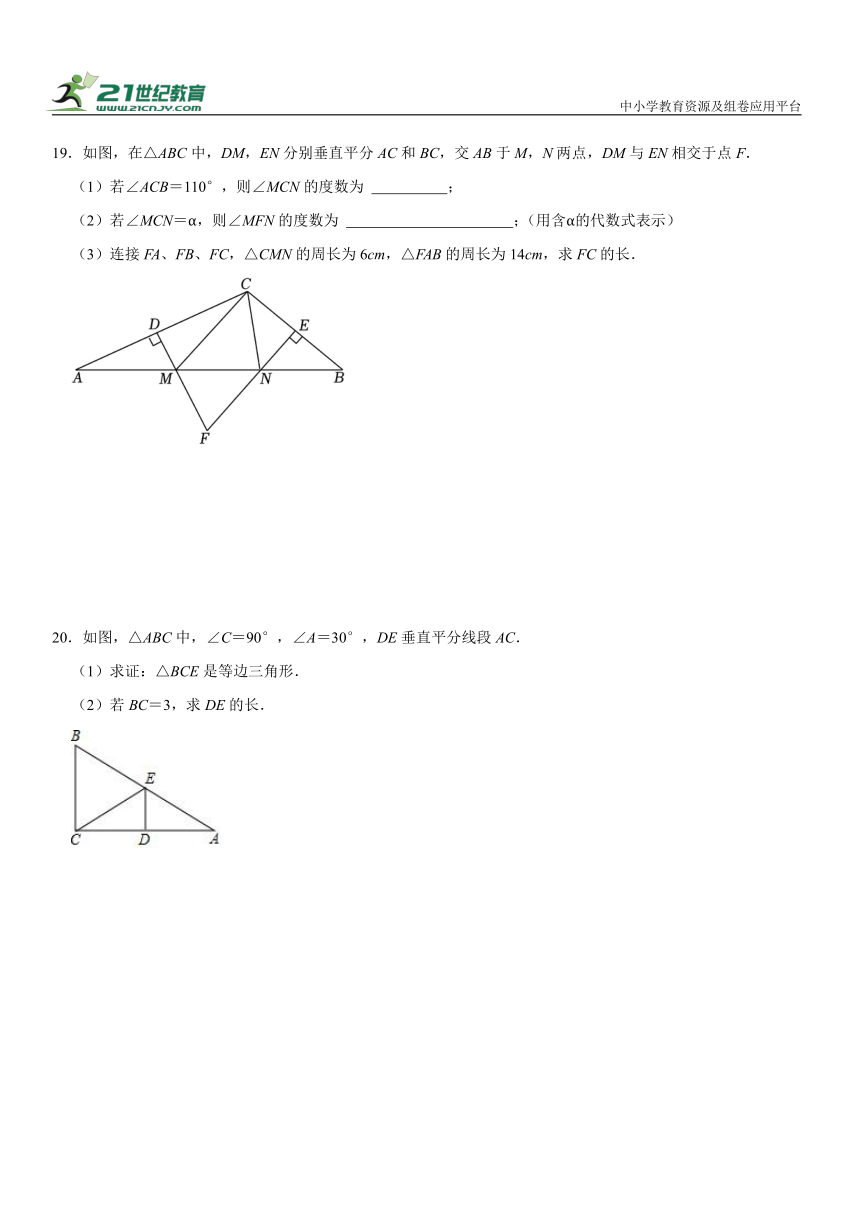
15.如图,△ABC的三个顶点坐标分别为A(2,3),B(1,1),C(5,3).
(1)作出△ABC关于y轴对称的图形△A1B1C1;
(2)求△A1B1C1的面积;
(3)在x轴上找一点P,使得PC+PB最小,请直接写出点P的坐标.
16.如图,在△ABC和△BDE中,点C在线段BD上,AC与BE交于点F.若AC=BD,BF=CF,BC=BE.
(1)求证:AB=DE;
(2)若∠D=58°,∠ABE=52°,求∠ACB的度数.
17.如图,△ABC中,D为BC的中点,连接AD并延长到E,使DE=AD.求证:∠C=∠EBC.
18.如图,四边形ABCD中,对角线AC,BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ABC=∠ACB=65°,求∠BDC的度数.
19.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 ;
(2)若∠MCN=α,则∠MFN的度数为 ;(用含α的代数式表示)
(3)连接FA、FB、FC,△CMN的周长为6cm,△FAB的周长为14cm,求FC的长.
20.如图,△ABC中,∠C=90°,∠A=30°,DE垂直平分线段AC.
(1)求证:△BCE是等边三角形.
(2)若BC=3,求DE的长.
人教版2024年八年级上册第11-13章阶段性基础提升练习
参考答案
一.选择题
1.【解答】解:根据三角形的三边关系,知
A、2+2=4,不能组成三角形;
B、3+6>8,能够组成三角形;
C、3+2=5<6,不能组成三角形;
D、4+6<11,不能组成三角形.
故选:B.
2.【解答】解:选项A、B、D的图形均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,
选项C的图形能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形.
故选:C.
3.【解答】解:设这个多边形的边数是n,
根据题意得,(n﹣2)×180°=3×360°﹣180°,
解得n=7,
故选:A.
4.【解答】解:由题意得,50°角对应的边长为10,
∴α=180°﹣50°﹣60°=70°,
∴70°角对应的边长为20,
∴x=20.
故选:D.
5.【解答】解:∵AB⊥BC,DE⊥AC
∴∠ABC=∠CED=90°,
在Rt△ABC与Rt△CED中,
,
∴Rt△ABC≌Rt△CED(HL),
故选:D.
6.【解答】解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
7.【解答】解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
根据两点之间,线段最短,可知选项C铺设的管道,则所需管道最短.
故选:C.
8.【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=12cm,DC=BE=28cm,
∴DE=DC+CE=40(cm),
答:两堵木墙之间的距离为40cm.
故选:A.
二.填空题
9.【解答】解:∵点A(a,4),点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
则(a+b)2023=(3﹣4)2023=﹣1;
故答案为:﹣1.
10.【解答】解:∵△AOD≌△BOC,∠A=30°,∠C=50°,
∴∠D=∠C=50°,
∵∠A=30°,
∴∠AOD=180°﹣∠A﹣∠D=180°﹣30°﹣50°=100°,
∵∠AOC=145°,
∴∠COD=∠AOC﹣∠AOD=145°﹣100°=45°,
故答案为:45°.
11.【解答】解:过D点作DE⊥AB于点E,则DE即为所求,
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DE(角的平分线上的点到角的两边的距离相等),
∵CD=5,
∴DE=5.
故答案为:5.
12.【解答】解:∵DE垂直平分AC,
∴AE=CE=3cm,AD=DC,
∵△ABD的周长为15cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=15cm,
∴△ABC的周长为:AB+BC+AC=AB+BC+AE+CE=15+3+3=21(cm),
故答案为:21cm.
13.【解答】解:当4cm为腰时,三边为4cm、4cm、6cm,可以构成三角形,
∴周长为:4+4+6=14(cm);
当6cm为腰时,三边为6cm、6cm、4cm,可以构成三角形,
∴周长为:6+6+4=16(cm);
综上,周长为14cm或16cm.
故答案为:14cm或16cm.
14.【解答】解:如图所示,连接CE,
∵AB=AC,AD⊥BC,
∴CD=BD,∠ADC=∠ADB=90°,
又∵DE=DE,
∴△CDE≌△BDE(SAS),
∴CE=BE,
∴BE+EF=CE+EF,
∴当C、E、F三点共线且CF⊥AB时CE+EF最小,即此时BE+EF最小,
∵∠BAC=40°,
∴∠BAD=∠BAC=20°,
同理可得CE′=BE′,则∠CBE′=∠BCE′=20°,
∴∠BE′F′=∠CBE′+∠BCE′=40°,
∴当BE+EF取得最小值时,∠BEF的度数为40°,
故答案为:40°.
三.解答题
15.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2),
答:△A1B1C1的面积是3;
(3)如图所示,点P即为所求;
∴P(2,0).
16.【解答】(1)证明:∵BF=CF,
∴∠FCB=∠FBC,
在△ABC与△DEB中,
,
∴△ABC≌△DEB(SAS),
∴AB=DE;
(2)解:由(1)知,△ABC≌△DEB,
∴∠A=∠D=58°,
∵∠A+∠ABE+∠FBC+∠FCB=180°,∠FBC=∠FCB,
∴58°+∠52°+2∠ACB=180°,
∴∠ACB=35°.
17.【解答】证明:∵D为BC的中点,
∴BD=DC,
∵∠BDE=∠CDA,DE=AD,
∴△BDE≌△CDA(SAS),
∴∠C=∠EBC.
18.【解答】(1)证明:∵∠BAC=∠EAD,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABD=∠ACD;
(2)解:∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∵∠ABD=∠ACD,
∴∠BAC=∠BDC,
∵∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=180°﹣130°=50°,
∴∠BDC=∠BAC=50°.
19.【解答】解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=110°,
∴∠A+∠B=70°,
∴∠A+∠B+∠ACM+∠BCN=140°,
∴∠MCN=40°,
故答案为:40°;
(2)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠MCN=α,
∴,
∴,
∵∠ACB+∠MFN=180°,
∴,
故答案为:;
(3)如图,
∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB,
∵△CMN的周长为6cm,
∴AB=6cm,
∵△FAB的周长为14cm,
∴FA+FB+AB=14cm,
∴FA+FB=8cm,
∵DF,EF分别垂直平分AC和BC,
∴FA=FC,FB=FC,
∴2FC=8cm,
∴FC=4cm.
20.【解答】证明:(1)在△ABC中,
∵∠B=180°﹣∠C﹣∠A=180°﹣90°﹣30°=60°,
∵DE垂直平分AC,
∴EC=EA,
∴∠ECA=∠A=30°,
∴∠BCE=60°,
∴△BCE是等边三角形;
(2)由(1)得,EC=BC=3,
Rt△ECD中,∵∠ECD=30°,
∴DE=EC=.
人教版2024年八年级上册第11-13章阶段性基础提升练习
一.选择题
1.以下列各组线段为边,能组成三角形的是( )
A.2、2、4 B.8、6、3 C.2、6、3 D.11、4、6
2.下列图形中,是轴对称图形的是( )
A. B.
C. D.
3.一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是( )
A.七 B.八 C.九 D.十
4.若图中的两个三角形全等,则依据所标数据可得( )
A.α=50° B.α=60° C.x=18 D.x=20
5.如图,AB⊥BC于B,DE⊥AC于E,AB=CE,AC=CD.则△ABC≌△CED的理由是( )
A.SSS B.SAS C.ASA D.HL
6.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
7.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
A. B.
C. D.
8.如图,小虎用10块高度都是4cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离DE的长度为( )
A.40cm B.36cm C.27cm D.24cm
二.填空题
9.点A(a,4),点B(3,b)关于x轴对称,则(a+b)2023= .
10.如图,△AOD≌△BOC,∠A=30°,∠C=50°,∠AOC=145°,则∠COD= .
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,且CD=5,则点D到AB的距离为 .
12.如图,在ABC中,DE垂直平分AC,交AC边于点E,交BC边于点D,若AE=3cm,△ABD的周长为15cm,则△ABC的周长为 .
13.等腰三角形的一条边长为4cm,另一条边长为6cm,则它的周长是 .
14.如图,在等腰△ABC中,AB=AC,AD⊥BC于点D,E、F两动点分别在线段AD、AB上运动,若∠BAC=40°,则当BE+EF取得最小值时,∠BEF的度数为 .
三.解答题
15.如图,△ABC的三个顶点坐标分别为A(2,3),B(1,1),C(5,3).
(1)作出△ABC关于y轴对称的图形△A1B1C1;
(2)求△A1B1C1的面积;
(3)在x轴上找一点P,使得PC+PB最小,请直接写出点P的坐标.
16.如图,在△ABC和△BDE中,点C在线段BD上,AC与BE交于点F.若AC=BD,BF=CF,BC=BE.
(1)求证:AB=DE;
(2)若∠D=58°,∠ABE=52°,求∠ACB的度数.
17.如图,△ABC中,D为BC的中点,连接AD并延长到E,使DE=AD.求证:∠C=∠EBC.
18.如图,四边形ABCD中,对角线AC,BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ABC=∠ACB=65°,求∠BDC的度数.
19.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 ;
(2)若∠MCN=α,则∠MFN的度数为 ;(用含α的代数式表示)
(3)连接FA、FB、FC,△CMN的周长为6cm,△FAB的周长为14cm,求FC的长.
20.如图,△ABC中,∠C=90°,∠A=30°,DE垂直平分线段AC.
(1)求证:△BCE是等边三角形.
(2)若BC=3,求DE的长.
人教版2024年八年级上册第11-13章阶段性基础提升练习
参考答案
一.选择题
1.【解答】解:根据三角形的三边关系,知
A、2+2=4,不能组成三角形;
B、3+6>8,能够组成三角形;
C、3+2=5<6,不能组成三角形;
D、4+6<11,不能组成三角形.
故选:B.
2.【解答】解:选项A、B、D的图形均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,
选项C的图形能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形.
故选:C.
3.【解答】解:设这个多边形的边数是n,
根据题意得,(n﹣2)×180°=3×360°﹣180°,
解得n=7,
故选:A.
4.【解答】解:由题意得,50°角对应的边长为10,
∴α=180°﹣50°﹣60°=70°,
∴70°角对应的边长为20,
∴x=20.
故选:D.
5.【解答】解:∵AB⊥BC,DE⊥AC
∴∠ABC=∠CED=90°,
在Rt△ABC与Rt△CED中,
,
∴Rt△ABC≌Rt△CED(HL),
故选:D.
6.【解答】解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
7.【解答】解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
根据两点之间,线段最短,可知选项C铺设的管道,则所需管道最短.
故选:C.
8.【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=12cm,DC=BE=28cm,
∴DE=DC+CE=40(cm),
答:两堵木墙之间的距离为40cm.
故选:A.
二.填空题
9.【解答】解:∵点A(a,4),点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
则(a+b)2023=(3﹣4)2023=﹣1;
故答案为:﹣1.
10.【解答】解:∵△AOD≌△BOC,∠A=30°,∠C=50°,
∴∠D=∠C=50°,
∵∠A=30°,
∴∠AOD=180°﹣∠A﹣∠D=180°﹣30°﹣50°=100°,
∵∠AOC=145°,
∴∠COD=∠AOC﹣∠AOD=145°﹣100°=45°,
故答案为:45°.
11.【解答】解:过D点作DE⊥AB于点E,则DE即为所求,
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DE(角的平分线上的点到角的两边的距离相等),
∵CD=5,
∴DE=5.
故答案为:5.
12.【解答】解:∵DE垂直平分AC,
∴AE=CE=3cm,AD=DC,
∵△ABD的周长为15cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=15cm,
∴△ABC的周长为:AB+BC+AC=AB+BC+AE+CE=15+3+3=21(cm),
故答案为:21cm.
13.【解答】解:当4cm为腰时,三边为4cm、4cm、6cm,可以构成三角形,
∴周长为:4+4+6=14(cm);
当6cm为腰时,三边为6cm、6cm、4cm,可以构成三角形,
∴周长为:6+6+4=16(cm);
综上,周长为14cm或16cm.
故答案为:14cm或16cm.
14.【解答】解:如图所示,连接CE,
∵AB=AC,AD⊥BC,
∴CD=BD,∠ADC=∠ADB=90°,
又∵DE=DE,
∴△CDE≌△BDE(SAS),
∴CE=BE,
∴BE+EF=CE+EF,
∴当C、E、F三点共线且CF⊥AB时CE+EF最小,即此时BE+EF最小,
∵∠BAC=40°,
∴∠BAD=∠BAC=20°,
同理可得CE′=BE′,则∠CBE′=∠BCE′=20°,
∴∠BE′F′=∠CBE′+∠BCE′=40°,
∴当BE+EF取得最小值时,∠BEF的度数为40°,
故答案为:40°.
三.解答题
15.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2),
答:△A1B1C1的面积是3;
(3)如图所示,点P即为所求;
∴P(2,0).
16.【解答】(1)证明:∵BF=CF,
∴∠FCB=∠FBC,
在△ABC与△DEB中,
,
∴△ABC≌△DEB(SAS),
∴AB=DE;
(2)解:由(1)知,△ABC≌△DEB,
∴∠A=∠D=58°,
∵∠A+∠ABE+∠FBC+∠FCB=180°,∠FBC=∠FCB,
∴58°+∠52°+2∠ACB=180°,
∴∠ACB=35°.
17.【解答】证明:∵D为BC的中点,
∴BD=DC,
∵∠BDE=∠CDA,DE=AD,
∴△BDE≌△CDA(SAS),
∴∠C=∠EBC.
18.【解答】(1)证明:∵∠BAC=∠EAD,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABD=∠ACD;
(2)解:∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∵∠ABD=∠ACD,
∴∠BAC=∠BDC,
∵∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=180°﹣130°=50°,
∴∠BDC=∠BAC=50°.
19.【解答】解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=110°,
∴∠A+∠B=70°,
∴∠A+∠B+∠ACM+∠BCN=140°,
∴∠MCN=40°,
故答案为:40°;
(2)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠MCN=α,
∴,
∴,
∵∠ACB+∠MFN=180°,
∴,
故答案为:;
(3)如图,
∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB,
∵△CMN的周长为6cm,
∴AB=6cm,
∵△FAB的周长为14cm,
∴FA+FB+AB=14cm,
∴FA+FB=8cm,
∵DF,EF分别垂直平分AC和BC,
∴FA=FC,FB=FC,
∴2FC=8cm,
∴FC=4cm.
20.【解答】证明:(1)在△ABC中,
∵∠B=180°﹣∠C﹣∠A=180°﹣90°﹣30°=60°,
∵DE垂直平分AC,
∴EC=EA,
∴∠ECA=∠A=30°,
∴∠BCE=60°,
∴△BCE是等边三角形;
(2)由(1)得,EC=BC=3,
Rt△ECD中,∵∠ECD=30°,
∴DE=EC=.
