数学:3.3相似三角形的性质和判定同步练习(湘教版九年级上)
文档属性
| 名称 | 数学:3.3相似三角形的性质和判定同步练习(湘教版九年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 54.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-29 08:48:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
3.3相似三角形的性质和判定同步练习
一、仔仔细细,记录自信
1.如图1,△OED∽△OCB,且OE=6,EC=21,则△OCB与△OED的相似比是( )
A. B. C. D.
2.如图2,点E,F分别在矩形ABCD的边DC,BC上,∠AEF=90°,∠AFB=2∠DAE=72°,则图中甲、乙、丙三个三角形中相似的是( )
A.只有甲与乙 B.只有乙与丙 C.只有甲与丙 D.甲与乙与丙
3.如图3,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
A.1 B.
C. D.
4.在相同水压下,口径为4cm的水管的出水量是口径为1cm的水管出水量的( )
A.4倍 B.8倍 C.12倍 D.16倍
5.对于下列说法:
(1)相似且有一边为公共边的两个三角形全等;
(2)相似且面积相等的两个三角形全等;
(3)相似且周长相等的两个三角形全等.
其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
6.我国国土面积约为960万平方千米,画在比例尺为1∶1 000万的地图上的面积约是( )
A.960平方千米 B.960平方米 C.960平方分米 D.960平方厘米
二、认认真真,书写快乐
7.已知,且,,则BC= .
8.两个相似三角形,其中一个三角形的两个内角分别是40°和30°,则另一个三角形的最大内角的度数是 .
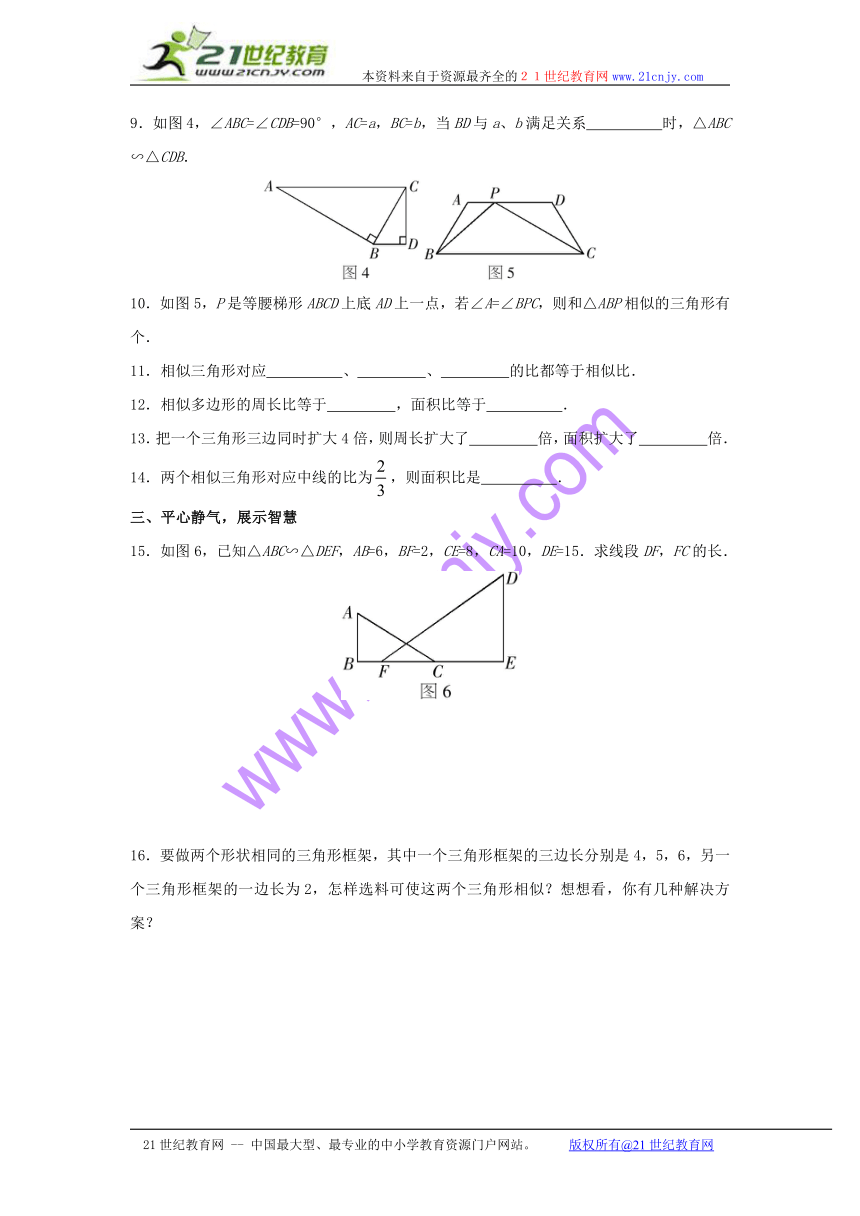
9.如图4,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b满足关系 时,△ABC∽△CDB.
10.如图5,P是等腰梯形ABCD上底AD上一点,若∠A=∠BPC,则和△ABP相似的三角形有 个.
11.相似三角形对应 、 、 的比都等于相似比.
12.相似多边形的周长比等于 ,面积比等于 .
13.把一个三角形三边同时扩大4倍,则周长扩大了 倍,面积扩大了 倍.
14.两个相似三角形对应中线的比为,则面积比是 .
三、平心静气,展示智慧
15.如图6,已知△ABC∽△DEF,AB=6,BF=2,CE=8,CA=10,DE=15.求线段DF,FC的长.
16.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别是4,5,6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?想想看,你有几种解决方案?
17.如图7,已知△ABC∽△DEF,AM、DN是中线,试判断△ABM与△DEN是否相似?为什么?
18.如图8,AD是△ABC角平分线,试判断是否成立?
3.3相似三角形的性质和判定试题练习答案
一、1~6.BDCDC D
二、7. 8. 9. 10.
11.高、中线、角平分线 12.相似比,相似比的平方 13., 14.
三、15.,.
16.可选料有三种方案,三角形框架边长分别是①,,;②,,;③,,.
17.相似;可用三边对应成比例或两边对应成比例且夹角相等说明.
18.过点作交延长线于点,则可得,
从而,然后再由,得,故成立.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
3.3相似三角形的性质和判定同步练习
一、仔仔细细,记录自信
1.如图1,△OED∽△OCB,且OE=6,EC=21,则△OCB与△OED的相似比是( )
A. B. C. D.
2.如图2,点E,F分别在矩形ABCD的边DC,BC上,∠AEF=90°,∠AFB=2∠DAE=72°,则图中甲、乙、丙三个三角形中相似的是( )
A.只有甲与乙 B.只有乙与丙 C.只有甲与丙 D.甲与乙与丙
3.如图3,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
A.1 B.
C. D.
4.在相同水压下,口径为4cm的水管的出水量是口径为1cm的水管出水量的( )
A.4倍 B.8倍 C.12倍 D.16倍
5.对于下列说法:
(1)相似且有一边为公共边的两个三角形全等;
(2)相似且面积相等的两个三角形全等;
(3)相似且周长相等的两个三角形全等.
其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
6.我国国土面积约为960万平方千米,画在比例尺为1∶1 000万的地图上的面积约是( )
A.960平方千米 B.960平方米 C.960平方分米 D.960平方厘米
二、认认真真,书写快乐
7.已知,且,,则BC= .
8.两个相似三角形,其中一个三角形的两个内角分别是40°和30°,则另一个三角形的最大内角的度数是 .
9.如图4,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b满足关系 时,△ABC∽△CDB.
10.如图5,P是等腰梯形ABCD上底AD上一点,若∠A=∠BPC,则和△ABP相似的三角形有 个.
11.相似三角形对应 、 、 的比都等于相似比.
12.相似多边形的周长比等于 ,面积比等于 .
13.把一个三角形三边同时扩大4倍,则周长扩大了 倍,面积扩大了 倍.
14.两个相似三角形对应中线的比为,则面积比是 .
三、平心静气,展示智慧
15.如图6,已知△ABC∽△DEF,AB=6,BF=2,CE=8,CA=10,DE=15.求线段DF,FC的长.
16.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别是4,5,6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?想想看,你有几种解决方案?
17.如图7,已知△ABC∽△DEF,AM、DN是中线,试判断△ABM与△DEN是否相似?为什么?
18.如图8,AD是△ABC角平分线,试判断是否成立?
3.3相似三角形的性质和判定试题练习答案
一、1~6.BDCDC D
二、7. 8. 9. 10.
11.高、中线、角平分线 12.相似比,相似比的平方 13., 14.
三、15.,.
16.可选料有三种方案,三角形框架边长分别是①,,;②,,;③,,.
17.相似;可用三边对应成比例或两边对应成比例且夹角相等说明.
18.过点作交延长线于点,则可得,
从而,然后再由,得,故成立.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
