第八单元数学广角-数与形(单元自测)-2024-2025学年小学数学六年级上册人教版(含解析)
文档属性
| 名称 | 第八单元数学广角-数与形(单元自测)-2024-2025学年小学数学六年级上册人教版(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 806.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-11 00:00:00 | ||
图片预览

文档简介
/ 让教学更有效 精品试卷 | 数学学科
第八单元数学广角-数与形(单元自测)-2024-2025学年小学数学六年级上册人教版
一、选择题
1.观察图形的规律,第6个图形一共由( )个小三角形组成。
……
A.25 B.36 C.38 D.49
2.搭建如图(1)所示的帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要( )根钢管。
A.340 B.225 C.226 D.227
3.选项( )中的图意,表示的是的。
A. B. C.
4.照下图的样子摆下去,如果一个小三角形的边长为1cm,第8个图形的周长是( )cm。
A.8 B.10 C.17 D.24
5.如下图,第8个点阵的点数是( )个。
A.36 B.35 C.32 D.28
二、填空题
6.如下图,如果不画图,这样排列下去,第10个图形是( )个圆。
7.观察下图,摆4个六边形需要( )根小棒,摆9个六边形需要( )根小棒。2·1·c·n·j·y
8.找规律填空:,,,……则( )。如图的方式摆棋子,摆第6个图案时需要( )枚棋子;摆第( )个图案时需要206枚棋子。2-1-c-n-j-y
9.一次射击练习中,命中的子弹是100发,没命中的是25发,命中率是( )。
10.按左图中的规律摆六边形,摆6个六边形需要( )根小棒。
11.找规律在空格或括号里填上适当的数。
12.如图,给正五边形的顶点依次编号为1,2,3,4,5。若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”。如:小宇在编号为3的顶点时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”。若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是( )。21*cnjy*com
13.用相同长度的小棒摆成一组有规律的图案,如图所示。第1个图案需要4根小棒,第2个图案需要10根小棒……按此规律摆下去,第7个图案需要( )根小棒。
14.
上图中②中有( )个小正方体,③中有( )个小正方体.按照这种方法继续摆下去,第5个图有( )个小正方体,第9个图有( )个小正方体.
三、判断题
15.在中,从“1”到“15”的和是64.( )
16.要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制扇形统计图。( )
17.++++…=1。( )
18.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3.
19.如图,用小棒摆图形,摆第8个用了17根小棒。( )
四、计算题
20.找规律,算一算。
(1) (2)5+7+9+11+13+…+25
五、作图题
21.找规律,画一画。
六、解答题
22.现有a(a>50)根长度相同的小棒,按图1摆放恰好可以摆成2m个三角形,按图2摆放恰好可以摆成2n个小正方形。www.21-cn-jy.com
(1)求a的最小值;
(2)若这a根小棒还可以按图3恰好摆成p个五边形,且a<200,求a的最大值。
23.观察下面图中的点群,请回答:
方框内的点群包含多少个点?推测第10个点群中包含多少个点?前10个点群中,所有点的总数是多少?
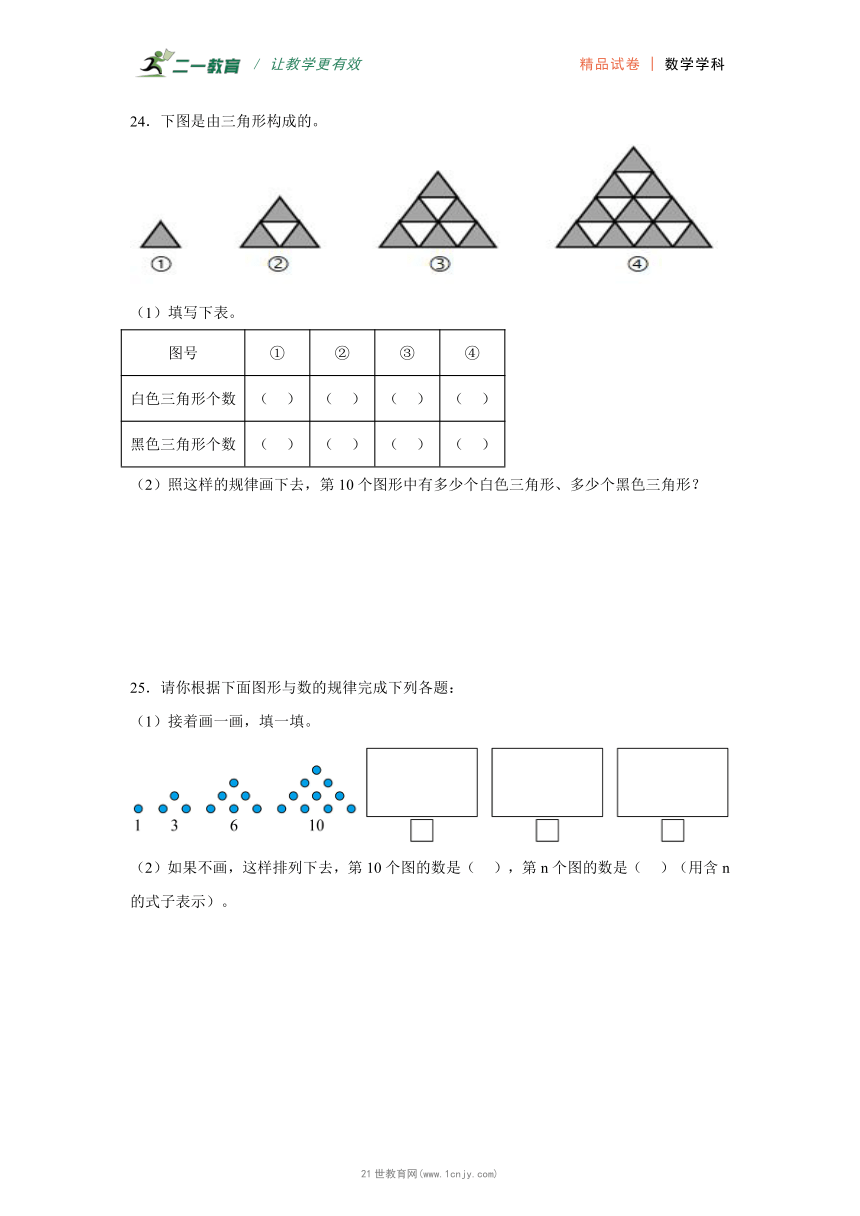
24.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
25.请你根据下面图形与数的规律完成下列各题:
(1)接着画一画,填一填。
(2)如果不画,这样排列下去,第10个图的数是( ),第n个图的数是( )(用含n的式子表示)。21世纪教育网版权所有
26.观察下面的点阵图和相应的等式,探究其中的规律。
(1)在④和⑤后面的横线上分别写出相应的等式;
①;②;③;④______________;⑤______________;…
(2)如果这样排列下去,第10个图形中有多少个圆点?
27.如图,一张桌子可以坐6个人,两张桌子可以坐10个人,那么10张桌子可以坐多少个人?
28.在数图形中包含的长方形个数时,可以用下面的方法快速算出图中的长方形个数。例如:
1 2 3
2
(1+2+3)×(1+2)=18(个)
照样子算一算,下图中共有多少个长方形(包含正方形)?
29.观察思考并计算。
(1)观察下面每个图形中小正方形的排列规律,并填空。
( ) ( )
(2)根据上面的规律用简便方法计算。
( )×( )=( )。
参考答案:
1.B
【分析】观察图形可知,第1个图中有1个三角形,可以写成12;第2个图形有1+3=4个三角形,可以写成22;第3个图形有1+3+5=9个三角形,可以写成32;第4个图形中有1+3+5+7=16个三角形,可以写成42,那么第n个图形有n2个三角形.据此即可解答。
【详解】第1个图中有1=12个三角形;
第2个图形有1+3=22个三角形;
第3个图形有1+3+5=32个三角形;
第4个图形中有1+3+5+7=42个三角形,
……
所以第n个图形有n2个三角形,
当n=6时,图中有三角形:62=36(个)。
故答案为:B
【点睛】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。21cnjy.com
2.C
【详解】略
3.C
【详解】略
4.B
【分析】第一个图形的周长是3cm,可以写成:(1+2)cm,第二个图形的周长是4cm,可以写成:(2+2)cm,第三个图形的周长是5cm,可以写成:(3+2)cm,…,由此可知,每增加一个三角形周长就多1cm,所以第n个图形的周长=(n+2)cm。
【详解】根据分析可知,第8个图形的周长是:8+2=10(cm)
照下图的样子摆下去,如果一个小三角形的边长为1cm,第8个图形的周长是10cm。
故答案为:B
5.A
【分析】根据点阵中点子的排列规律可知:第1个点阵有1个点;第2个点阵有1+2=3(个)点;第3个点阵有1+2+3=6(个)点;……根据规律做题即可。21·cn·jy·com
【详解】第1个点阵有1个点;
第2个点阵有1+2=3(个)点;
第3个点阵有1+2+3=6(个)点;
……
第8个点阵有点数:
1+2+3+……+8
=8×9÷2
=36(个)
第8个点阵的点数是36个。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
6.55
【分析】观察图形可知,第一个图形有1个圆,第二个图形有3个圆,第三个图形有6个圆,第四个图形有10个圆,则第n个图形有(n+1)n÷2个圆,据此解答即可。
【详解】第10个图形圆的个数:
(10+1)×10÷2
=11×10÷2
=110÷2
=55(个)
【点睛】本题考查找规律,发现规律,利用规律是解题的关键。
7. 21 46
【分析】观察图形,第一个六边形有6根小棒,第二个六边形有(6+5)根小棒,第三个六边形有(6+5×2)根小棒,第四个六边形有(6+5×3)根小棒,依次类推,求出答案。
【详解】摆4个六边形需要(6+5×3)=21根小棒,摆9个六边形需要(6+5×8)=46根小棒。
【点睛】解决此题的关键是观察图形中数量的变换规律,利用数与形的相互联系,解决问题。
8. 502 20 68
【分析】观察算式可知,算式的结果为第一个数与最后一个数的和除以2的平方,据此填空;观察图案可知,第一个图案有5枚棋子,第二个图案有5+3枚棋子,第三个图案有5+3+3枚棋子,所以第n个图形就有5+(n-1)×3=3n+2枚棋子,据此填空。
【详解】(1+99)÷2
=100÷2
=50
502;
第n个图形就有3n+2枚棋子
但n=6时
3×6+2=20,第6个图案有20枚棋子;
当3n+2=206时
解:3n=204
n=68
摆第68个图案时需要206枚棋子。
【点睛】此题考查了根据算式找规律以及根据图形找规律,认真观察解答即可。
9.80%
【分析】命中率=命中数÷总数×100%,据此解答即可。
【详解】100÷(100+25)×100%
=100÷125×100%
=0.8×100%
=80%
【点睛】本题主要考查对命中率的理解与运用。
10.31
【分析】从图中可知,摆1个六边形需要6根小棒,摆2个六边形需要11根小棒,摆3个六边形需要16根小棒,……;每增加一个六边形,增加5根小棒,据此找到规律,并按规律解答。【版权所有:21教育】
【详解】摆1个六边形需要6根小棒,6=5×1+1;
摆2个六边形需要11根小棒,11=5×2+1;
摆3个六边形需要16根小棒,16=5×3+1;
……
摆6个三角形需要小棒:
5×6+1
=30+1
=31(根)
摆6个六边形需要31根小棒。
【点睛】本题是找规律的题型,从已知的图形或数据中找到规律,并按规律解题。
11.
【分析】观察题干可知,前面的两个图形中,上面数字之和等于第三个图形的上面数字;所以可得:右面或左面的两个数字之和,也等于第三个图形中的右面或左面数字,据此即可解答。21教育名师原创作品
【详解】根据题干分析可得:12+12=24,16+10=26。
填图如下:
【点睛】本题考查了数与形,有一定抽象概括能力是解题的关键。
12.3
【分析】根据“移位”的特点确定出前几次的移位情况,从而找出规律,然后解答即可。
【详解】根据题意,小宇从编号为2的顶点开始,第1次移位到点4,第2次移位到达点3,第3次移位到达点1,第4次移位到达点2,…,依此类推,4次移位后回到出发点,
10÷4=2……2
所以第10次移位为第3个循环组的第2次移位,到达点3。
【点睛】本题对图形变化规律的考查,根据“移位”的定义,找出每4次移位为一个循环组进行循环是解题的关键。
13.40
【分析】通过观察可知,在原有图形的基础上依次增加两个正方形,每增加两个正方形需要6根小棒,那么第个图案在4根的基础上,需要增加6的倍个小棒,据此解答。
【详解】
根
当时
(根)
第7个图案需要40根小棒。
14. 4 10 35 81
【解析】略
15.√
【分析】在1+3+5+7+9+…中首先求出“15”是第几项(由于项数比较少,可能用数的方法),由于相邻两数的差是1,所以项数等于(未项一首项)÷2+1,据即可求15是第几项;前n项和的计算公式是(未项+首项)×,根据公式可求出和,根据计算结果进行判断.
【详解】在1+3+5+7+9+…中,从“1”到数“15”的项数为:(15-1)÷2+1=14÷2+1=7+1=8;和为:(15+1)× =16×4=64【出处:21教育名师】
因此,在1+3+5+7+9+…中,从“1”到数“15”的和是64,原题的说法正确。
故答案为:√.
【点睛】此题项数较少,写出所有项,通过计算即可得到正确的结果.如果项数较多,只能先总结出求项数、前n项和公式解答。
16.×
【分析】扇形统计图主要表示部分与部分之间,部分与总体之间的数量关系,以及各部分量占总体的百分比情况,要具体的数量选择条形统计图更加合适,据此解答。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;因此要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制条形统计图。
故答案为:×
【点睛】根据统计图的特征选择合适的统计图是解答题目的关键。
17.√
【分析】根据分数的加减法的关系和性质,将++++…进行简算即可。
【详解】++++…
=(1-)+(-)+(-)+(-)+…
=1-+-+-+-+…
=1
所以原题干说法正确。
故答案为:√
【点睛】本题考查了分数加减法的灵活应用。
18.×
【详解】20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为×
19.√
【分析】根据图示发现:摆1个三角形需要小棒:3根;摆2个三角形需要小棒(3+2)根;摆3个三角形需要小棒(3+2+2)根;……摆n个三角形需要小棒的根数是3+2(n-1)。据此解答。21*cnjy*com
【详解】摆n个三角形需要小棒
3+2(n-1)
=3+2n-2
=(2n+1)根
当n=8时,
2×8+1
=16+1
=17(根)
用小棒摆图形,摆第8个用了17根小棒。此说法正确。
故答案为:√
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
20.(1);(2)165
【分析】(1)将拆成(1-),拆成(-),拆成(-),拆成(-),拆成(-),再去括号,括号前边是减号,去掉括号,括号里的减号变加号,前边抵消后,只剩下,据此计算;21教育网
(2)可以将数列分为5对数, 每对数的和都是30,即(5+25)+(7+23)+(9+21)+(11+19)+(13+17) , 除了中间的15,先计算出5对数的和,再加上15即可。
【详解】(1)
=
=
=
(2) 5+7+9+11+13+…+25
=(5+25)+(7+23)+(9+21)+(11+19)+(13+17)+15
=30×5+15
=150+15
=165
【点睛】较复杂的分数加运算可以利用裂项以及转化法解决计算是解答本题的关键。
21.见详解
【分析】依次是5个△,4个△,3个△,2个△,1个△;据此解决即可。
【详解】由题意分析得:
22.(1)57;(2)177
【分析】(1)对图1分析:
m=1时,就是有2个三角形时,需要5=1+4根小棒;
m=2时,就是有4个三角形时,需要9=1+4×2根小棒;
m=3时,就是有6个三角形时,需要13=1+4×3根小棒;
……
需要小棒的数量=1+4m。
对图2分析:
n=1时,就是2个正方形时,需要7=2+5根小棒;
n=2时,就是4个正方形时,需要12=2+5×2根小棒;
n=3时,就是6个正方形时,需要17=2+5×3根小棒;
……
需要小棒的数量=2+5n。
摆成两种图形小棒的数量是一样的,则
a=1+4m=2+5n,a的值大于50,则m最小13,n最小是10,且m、n、a都是整数。当m=13时,n=10.2不符合;m=14时,n=11符合。 【来源:21cnj*y.co*m】
(2)分析图3:
p=2时,就是有2个五边形,需要小棒9根小棒;
p=4时,就是有4个五边形,需要小棒15=3×4+3根小棒;
p=6时,就是有6个五边形,需要小棒21=3×6+3根小棒;
……
需要小棒的根数=3p+3=3(p+1),即a的值是3的倍数,在满足(1)的情况下,a的取值是:57、77、97、117、137、157、177,
其中77、97、137、157不是3的倍数,57、117、177是3的倍数。
【详解】(1)摆成三角形需要小棒的数量:1+4m。
摆成正方形需要小棒的数量:2+5n。
1+4m=5n+2
4m=5n+1
m=
当m=14,n=11时,
1+4×14
=1+56
=57(根)
答:a的最小值57根。
(2)a=3(p+1)
a的取值是:57、77、97、117、137、157、177,
57、117、177是3的倍数,177最大。
答:a的最大值177根。
【点睛】认真观察图形,找出图形的变化规律是解题关键。
23.25个;100个;385个
【分析】观察前4幅图,发现其排列规律为自然数的平方数,故第5幅图包含25个点;第10幅图包含100个点;再把前10幅图的点累计起来,就是所有点的总数。
【详解】5×5=25(个);
10×10=100(个);
1+4+9+16+25+36+49+64+81+100
=285+100
=385(个)
答:所有点的总数为385个。
【点睛】学方的知识点之后,对于这样呈现的图形就不陌生了,所以本题关键是解读点的排列规律。
24.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。21·世纪*教育网
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
25.(1)15;21;28;(2)55;
【分析】(1)通过观察,第1个图中有1个点,第2个图中有(1+2)个点,第3个图中有(1+2+3)个点,第4个图中有(1+2+3+4)个点,第几个图形的点数和等于前一个图形的点数和加几。【来源:21·世纪·教育·网】
(2)通过(1)类推,第n个图中有(1+2+3+…+n)个点,然后通过首尾相加进行化简即可。
【详解】(1)第5个图形:10+5=15(个)
第6个图形:15+6=21(个)
第7个图形:21+7=28(个)
(2)第n个图的数:
1+2+3+…+n
=(1+n)×n÷2
=(n+n2)÷2
=
当n=10时,
=
=
=
=55
第10个图的数是55;第n个图的数是。
26.(1);;
(2)100个
【分析】(1)根据所给图形即可得到所填的式子;
(2)从题意分析可得,从1开始的连续奇数之和等于数个数的平方,用n表示第n个图形以及数的个数,对应的等式规律为:1+3+5+…+(2n 1)=n2,根据找出的规律可得第10个图形对应的等式。
【详解】(1);
(2)1+3+5+7+9+11+13+15+17+19
=102
=100
答:如果这样排列下去,第10个图形中有100个圆点。
【点睛】此题考查了规律型:数字的变化类,找出题中的规律是解本题的关键。
27.42人
【详解】10×4+2=42(人)
28.100个(图见详解)
【分析】根据题意可知,把第一排从左往右每个小长方形按顺序填数,从1开始,后面的数每次增加1;同样把第一列从上往下每个小长方形(或正方形)按顺序填数,从1开始,后面的数每次增加1;然后分别把第一排和第一列上的数相加,再把相加的和相乘,所得的积就是图中的长方形(包含正方形)的个数。www-2-1-cnjy-com
【详解】
(1+2+3+4)×(1+2+3+4)
=10×10
=100(个)
答:图中共有100个长方形(包含正方形)。
【点睛】分析清楚例子中数长方形个数的规律是解答本题的关键。
29.(1) 4 5
(2) 10 11 110
【分析】(1)通过观察图形中小正方形的排列规律,发现了连续偶数相加的求和规律。
4
5
发现了连续偶数相加的求和规律:从2开始的连续n个偶数相加,其和为n×(n+1)
(2)在中,一共有10个偶数相加,然后运用发现的这个规律来计算即可。
【详解】(1)4,5
(2)
=10×(10+1)
=10×11
=110
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
第八单元数学广角-数与形(单元自测)-2024-2025学年小学数学六年级上册人教版
一、选择题
1.观察图形的规律,第6个图形一共由( )个小三角形组成。
……
A.25 B.36 C.38 D.49
2.搭建如图(1)所示的帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要( )根钢管。
A.340 B.225 C.226 D.227
3.选项( )中的图意,表示的是的。
A. B. C.
4.照下图的样子摆下去,如果一个小三角形的边长为1cm,第8个图形的周长是( )cm。
A.8 B.10 C.17 D.24
5.如下图,第8个点阵的点数是( )个。
A.36 B.35 C.32 D.28
二、填空题
6.如下图,如果不画图,这样排列下去,第10个图形是( )个圆。
7.观察下图,摆4个六边形需要( )根小棒,摆9个六边形需要( )根小棒。2·1·c·n·j·y
8.找规律填空:,,,……则( )。如图的方式摆棋子,摆第6个图案时需要( )枚棋子;摆第( )个图案时需要206枚棋子。2-1-c-n-j-y
9.一次射击练习中,命中的子弹是100发,没命中的是25发,命中率是( )。
10.按左图中的规律摆六边形,摆6个六边形需要( )根小棒。
11.找规律在空格或括号里填上适当的数。
12.如图,给正五边形的顶点依次编号为1,2,3,4,5。若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”。如:小宇在编号为3的顶点时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”。若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是( )。21*cnjy*com
13.用相同长度的小棒摆成一组有规律的图案,如图所示。第1个图案需要4根小棒,第2个图案需要10根小棒……按此规律摆下去,第7个图案需要( )根小棒。
14.
上图中②中有( )个小正方体,③中有( )个小正方体.按照这种方法继续摆下去,第5个图有( )个小正方体,第9个图有( )个小正方体.
三、判断题
15.在中,从“1”到“15”的和是64.( )
16.要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制扇形统计图。( )
17.++++…=1。( )
18.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3.
19.如图,用小棒摆图形,摆第8个用了17根小棒。( )
四、计算题
20.找规律,算一算。
(1) (2)5+7+9+11+13+…+25
五、作图题
21.找规律,画一画。
六、解答题
22.现有a(a>50)根长度相同的小棒,按图1摆放恰好可以摆成2m个三角形,按图2摆放恰好可以摆成2n个小正方形。www.21-cn-jy.com
(1)求a的最小值;
(2)若这a根小棒还可以按图3恰好摆成p个五边形,且a<200,求a的最大值。
23.观察下面图中的点群,请回答:
方框内的点群包含多少个点?推测第10个点群中包含多少个点?前10个点群中,所有点的总数是多少?
24.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
25.请你根据下面图形与数的规律完成下列各题:
(1)接着画一画,填一填。
(2)如果不画,这样排列下去,第10个图的数是( ),第n个图的数是( )(用含n的式子表示)。21世纪教育网版权所有
26.观察下面的点阵图和相应的等式,探究其中的规律。
(1)在④和⑤后面的横线上分别写出相应的等式;
①;②;③;④______________;⑤______________;…
(2)如果这样排列下去,第10个图形中有多少个圆点?
27.如图,一张桌子可以坐6个人,两张桌子可以坐10个人,那么10张桌子可以坐多少个人?
28.在数图形中包含的长方形个数时,可以用下面的方法快速算出图中的长方形个数。例如:
1 2 3
2
(1+2+3)×(1+2)=18(个)
照样子算一算,下图中共有多少个长方形(包含正方形)?
29.观察思考并计算。
(1)观察下面每个图形中小正方形的排列规律,并填空。
( ) ( )
(2)根据上面的规律用简便方法计算。
( )×( )=( )。
参考答案:
1.B
【分析】观察图形可知,第1个图中有1个三角形,可以写成12;第2个图形有1+3=4个三角形,可以写成22;第3个图形有1+3+5=9个三角形,可以写成32;第4个图形中有1+3+5+7=16个三角形,可以写成42,那么第n个图形有n2个三角形.据此即可解答。
【详解】第1个图中有1=12个三角形;
第2个图形有1+3=22个三角形;
第3个图形有1+3+5=32个三角形;
第4个图形中有1+3+5+7=42个三角形,
……
所以第n个图形有n2个三角形,
当n=6时,图中有三角形:62=36(个)。
故答案为:B
【点睛】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。21cnjy.com
2.C
【详解】略
3.C
【详解】略
4.B
【分析】第一个图形的周长是3cm,可以写成:(1+2)cm,第二个图形的周长是4cm,可以写成:(2+2)cm,第三个图形的周长是5cm,可以写成:(3+2)cm,…,由此可知,每增加一个三角形周长就多1cm,所以第n个图形的周长=(n+2)cm。
【详解】根据分析可知,第8个图形的周长是:8+2=10(cm)
照下图的样子摆下去,如果一个小三角形的边长为1cm,第8个图形的周长是10cm。
故答案为:B
5.A
【分析】根据点阵中点子的排列规律可知:第1个点阵有1个点;第2个点阵有1+2=3(个)点;第3个点阵有1+2+3=6(个)点;……根据规律做题即可。21·cn·jy·com
【详解】第1个点阵有1个点;
第2个点阵有1+2=3(个)点;
第3个点阵有1+2+3=6(个)点;
……
第8个点阵有点数:
1+2+3+……+8
=8×9÷2
=36(个)
第8个点阵的点数是36个。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
6.55
【分析】观察图形可知,第一个图形有1个圆,第二个图形有3个圆,第三个图形有6个圆,第四个图形有10个圆,则第n个图形有(n+1)n÷2个圆,据此解答即可。
【详解】第10个图形圆的个数:
(10+1)×10÷2
=11×10÷2
=110÷2
=55(个)
【点睛】本题考查找规律,发现规律,利用规律是解题的关键。
7. 21 46
【分析】观察图形,第一个六边形有6根小棒,第二个六边形有(6+5)根小棒,第三个六边形有(6+5×2)根小棒,第四个六边形有(6+5×3)根小棒,依次类推,求出答案。
【详解】摆4个六边形需要(6+5×3)=21根小棒,摆9个六边形需要(6+5×8)=46根小棒。
【点睛】解决此题的关键是观察图形中数量的变换规律,利用数与形的相互联系,解决问题。
8. 502 20 68
【分析】观察算式可知,算式的结果为第一个数与最后一个数的和除以2的平方,据此填空;观察图案可知,第一个图案有5枚棋子,第二个图案有5+3枚棋子,第三个图案有5+3+3枚棋子,所以第n个图形就有5+(n-1)×3=3n+2枚棋子,据此填空。
【详解】(1+99)÷2
=100÷2
=50
502;
第n个图形就有3n+2枚棋子
但n=6时
3×6+2=20,第6个图案有20枚棋子;
当3n+2=206时
解:3n=204
n=68
摆第68个图案时需要206枚棋子。
【点睛】此题考查了根据算式找规律以及根据图形找规律,认真观察解答即可。
9.80%
【分析】命中率=命中数÷总数×100%,据此解答即可。
【详解】100÷(100+25)×100%
=100÷125×100%
=0.8×100%
=80%
【点睛】本题主要考查对命中率的理解与运用。
10.31
【分析】从图中可知,摆1个六边形需要6根小棒,摆2个六边形需要11根小棒,摆3个六边形需要16根小棒,……;每增加一个六边形,增加5根小棒,据此找到规律,并按规律解答。【版权所有:21教育】
【详解】摆1个六边形需要6根小棒,6=5×1+1;
摆2个六边形需要11根小棒,11=5×2+1;
摆3个六边形需要16根小棒,16=5×3+1;
……
摆6个三角形需要小棒:
5×6+1
=30+1
=31(根)
摆6个六边形需要31根小棒。
【点睛】本题是找规律的题型,从已知的图形或数据中找到规律,并按规律解题。
11.
【分析】观察题干可知,前面的两个图形中,上面数字之和等于第三个图形的上面数字;所以可得:右面或左面的两个数字之和,也等于第三个图形中的右面或左面数字,据此即可解答。21教育名师原创作品
【详解】根据题干分析可得:12+12=24,16+10=26。
填图如下:
【点睛】本题考查了数与形,有一定抽象概括能力是解题的关键。
12.3
【分析】根据“移位”的特点确定出前几次的移位情况,从而找出规律,然后解答即可。
【详解】根据题意,小宇从编号为2的顶点开始,第1次移位到点4,第2次移位到达点3,第3次移位到达点1,第4次移位到达点2,…,依此类推,4次移位后回到出发点,
10÷4=2……2
所以第10次移位为第3个循环组的第2次移位,到达点3。
【点睛】本题对图形变化规律的考查,根据“移位”的定义,找出每4次移位为一个循环组进行循环是解题的关键。
13.40
【分析】通过观察可知,在原有图形的基础上依次增加两个正方形,每增加两个正方形需要6根小棒,那么第个图案在4根的基础上,需要增加6的倍个小棒,据此解答。
【详解】
根
当时
(根)
第7个图案需要40根小棒。
14. 4 10 35 81
【解析】略
15.√
【分析】在1+3+5+7+9+…中首先求出“15”是第几项(由于项数比较少,可能用数的方法),由于相邻两数的差是1,所以项数等于(未项一首项)÷2+1,据即可求15是第几项;前n项和的计算公式是(未项+首项)×,根据公式可求出和,根据计算结果进行判断.
【详解】在1+3+5+7+9+…中,从“1”到数“15”的项数为:(15-1)÷2+1=14÷2+1=7+1=8;和为:(15+1)× =16×4=64【出处:21教育名师】
因此,在1+3+5+7+9+…中,从“1”到数“15”的和是64,原题的说法正确。
故答案为:√.
【点睛】此题项数较少,写出所有项,通过计算即可得到正确的结果.如果项数较多,只能先总结出求项数、前n项和公式解答。
16.×
【分析】扇形统计图主要表示部分与部分之间,部分与总体之间的数量关系,以及各部分量占总体的百分比情况,要具体的数量选择条形统计图更加合适,据此解答。
【详解】条形统计图:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;因此要表示李爷爷家养的鸡、鸭、鹅的数量,应绘制条形统计图。
故答案为:×
【点睛】根据统计图的特征选择合适的统计图是解答题目的关键。
17.√
【分析】根据分数的加减法的关系和性质,将++++…进行简算即可。
【详解】++++…
=(1-)+(-)+(-)+(-)+…
=1-+-+-+-+…
=1
所以原题干说法正确。
故答案为:√
【点睛】本题考查了分数加减法的灵活应用。
18.×
【详解】20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为×
19.√
【分析】根据图示发现:摆1个三角形需要小棒:3根;摆2个三角形需要小棒(3+2)根;摆3个三角形需要小棒(3+2+2)根;……摆n个三角形需要小棒的根数是3+2(n-1)。据此解答。21*cnjy*com
【详解】摆n个三角形需要小棒
3+2(n-1)
=3+2n-2
=(2n+1)根
当n=8时,
2×8+1
=16+1
=17(根)
用小棒摆图形,摆第8个用了17根小棒。此说法正确。
故答案为:√
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
20.(1);(2)165
【分析】(1)将拆成(1-),拆成(-),拆成(-),拆成(-),拆成(-),再去括号,括号前边是减号,去掉括号,括号里的减号变加号,前边抵消后,只剩下,据此计算;21教育网
(2)可以将数列分为5对数, 每对数的和都是30,即(5+25)+(7+23)+(9+21)+(11+19)+(13+17) , 除了中间的15,先计算出5对数的和,再加上15即可。
【详解】(1)
=
=
=
(2) 5+7+9+11+13+…+25
=(5+25)+(7+23)+(9+21)+(11+19)+(13+17)+15
=30×5+15
=150+15
=165
【点睛】较复杂的分数加运算可以利用裂项以及转化法解决计算是解答本题的关键。
21.见详解
【分析】依次是5个△,4个△,3个△,2个△,1个△;据此解决即可。
【详解】由题意分析得:
22.(1)57;(2)177
【分析】(1)对图1分析:
m=1时,就是有2个三角形时,需要5=1+4根小棒;
m=2时,就是有4个三角形时,需要9=1+4×2根小棒;
m=3时,就是有6个三角形时,需要13=1+4×3根小棒;
……
需要小棒的数量=1+4m。
对图2分析:
n=1时,就是2个正方形时,需要7=2+5根小棒;
n=2时,就是4个正方形时,需要12=2+5×2根小棒;
n=3时,就是6个正方形时,需要17=2+5×3根小棒;
……
需要小棒的数量=2+5n。
摆成两种图形小棒的数量是一样的,则
a=1+4m=2+5n,a的值大于50,则m最小13,n最小是10,且m、n、a都是整数。当m=13时,n=10.2不符合;m=14时,n=11符合。 【来源:21cnj*y.co*m】
(2)分析图3:
p=2时,就是有2个五边形,需要小棒9根小棒;
p=4时,就是有4个五边形,需要小棒15=3×4+3根小棒;
p=6时,就是有6个五边形,需要小棒21=3×6+3根小棒;
……
需要小棒的根数=3p+3=3(p+1),即a的值是3的倍数,在满足(1)的情况下,a的取值是:57、77、97、117、137、157、177,
其中77、97、137、157不是3的倍数,57、117、177是3的倍数。
【详解】(1)摆成三角形需要小棒的数量:1+4m。
摆成正方形需要小棒的数量:2+5n。
1+4m=5n+2
4m=5n+1
m=
当m=14,n=11时,
1+4×14
=1+56
=57(根)
答:a的最小值57根。
(2)a=3(p+1)
a的取值是:57、77、97、117、137、157、177,
57、117、177是3的倍数,177最大。
答:a的最大值177根。
【点睛】认真观察图形,找出图形的变化规律是解题关键。
23.25个;100个;385个
【分析】观察前4幅图,发现其排列规律为自然数的平方数,故第5幅图包含25个点;第10幅图包含100个点;再把前10幅图的点累计起来,就是所有点的总数。
【详解】5×5=25(个);
10×10=100(个);
1+4+9+16+25+36+49+64+81+100
=285+100
=385(个)
答:所有点的总数为385个。
【点睛】学方的知识点之后,对于这样呈现的图形就不陌生了,所以本题关键是解读点的排列规律。
24.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。21·世纪*教育网
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
25.(1)15;21;28;(2)55;
【分析】(1)通过观察,第1个图中有1个点,第2个图中有(1+2)个点,第3个图中有(1+2+3)个点,第4个图中有(1+2+3+4)个点,第几个图形的点数和等于前一个图形的点数和加几。【来源:21·世纪·教育·网】
(2)通过(1)类推,第n个图中有(1+2+3+…+n)个点,然后通过首尾相加进行化简即可。
【详解】(1)第5个图形:10+5=15(个)
第6个图形:15+6=21(个)
第7个图形:21+7=28(个)
(2)第n个图的数:
1+2+3+…+n
=(1+n)×n÷2
=(n+n2)÷2
=
当n=10时,
=
=
=
=55
第10个图的数是55;第n个图的数是。
26.(1);;
(2)100个
【分析】(1)根据所给图形即可得到所填的式子;
(2)从题意分析可得,从1开始的连续奇数之和等于数个数的平方,用n表示第n个图形以及数的个数,对应的等式规律为:1+3+5+…+(2n 1)=n2,根据找出的规律可得第10个图形对应的等式。
【详解】(1);
(2)1+3+5+7+9+11+13+15+17+19
=102
=100
答:如果这样排列下去,第10个图形中有100个圆点。
【点睛】此题考查了规律型:数字的变化类,找出题中的规律是解本题的关键。
27.42人
【详解】10×4+2=42(人)
28.100个(图见详解)
【分析】根据题意可知,把第一排从左往右每个小长方形按顺序填数,从1开始,后面的数每次增加1;同样把第一列从上往下每个小长方形(或正方形)按顺序填数,从1开始,后面的数每次增加1;然后分别把第一排和第一列上的数相加,再把相加的和相乘,所得的积就是图中的长方形(包含正方形)的个数。www-2-1-cnjy-com
【详解】
(1+2+3+4)×(1+2+3+4)
=10×10
=100(个)
答:图中共有100个长方形(包含正方形)。
【点睛】分析清楚例子中数长方形个数的规律是解答本题的关键。
29.(1) 4 5
(2) 10 11 110
【分析】(1)通过观察图形中小正方形的排列规律,发现了连续偶数相加的求和规律。
4
5
发现了连续偶数相加的求和规律:从2开始的连续n个偶数相加,其和为n×(n+1)
(2)在中,一共有10个偶数相加,然后运用发现的这个规律来计算即可。
【详解】(1)4,5
(2)
=10×(10+1)
=10×11
=110
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
